固体磁性第六章

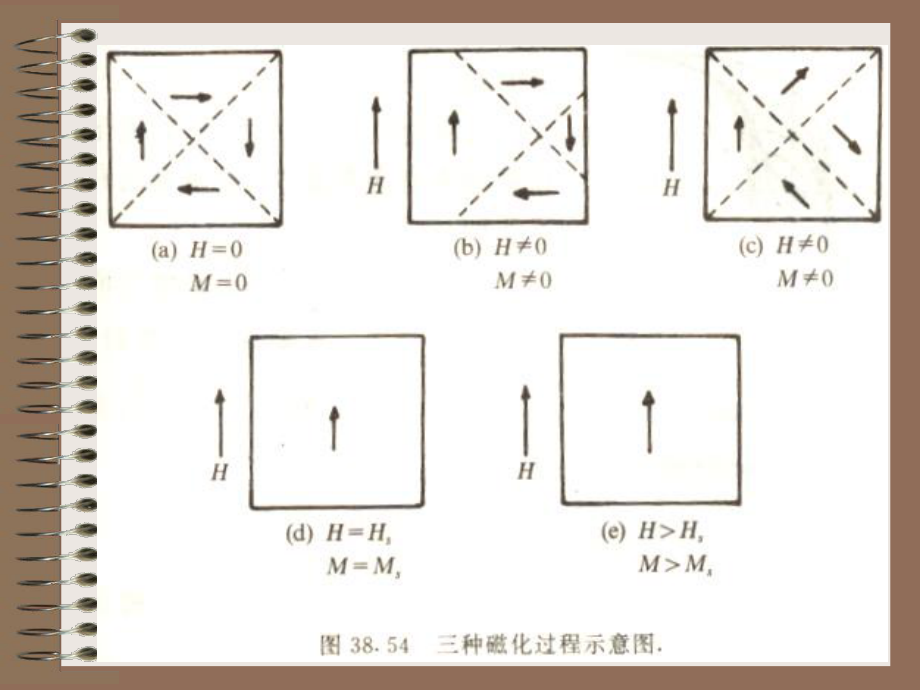
1、第六章第六章技术磁化基本原理技术磁化基本原理 1、 三种磁化过程三种磁化过程 iiisVMMcos退磁态 , 在外加磁场下, 磁化强度改变为0M HMisiiiiisiiisHMVVMVMMcoscoscosVi , 畴壁位移 DWD,cos i , 磁畴转动 DR,MS , 内禀磁化, 饱和磁化强度的增加,6 -1 磁化过程磁化过程, 磁化曲线及磁滞回线磁化曲线及磁滞回线 2、可逆及不可逆磁化、可逆及不可逆磁化初始磁化曲线磁滞回线* 可逆过程, RP较小的磁场变化也会产生较大的非连续的 变化, Barkhausen跳跃. 磁场有 变化时有滞后效应, 主要在磁化曲线及磁滞回线的陡峻部分.MH随

2、着外场H的变化,M连续变化. 对非常小的场变化H, M也变化很小并且是可逆的.主要在磁化曲线的初始部分及膝点以上部分.* 不可逆过程 , IRP, 导致回线. rriiirrmax,: 微增磁化率; r: 可逆; i: 初始; ir:不可逆. 3、磁化曲线及磁滞回线的基本特点、磁化曲线及磁滞回线的基本特点HM （1） 曲线 a、初始部分. 主要为RDWD 和RDR. b、陡峻部分. IRDWD (多畴) 为主; IRDR (单畴). c、膝点以上. 主要为 RDR .d、高场, 趋近饱和律. 顺行磁化过程.SM（2） 磁滞回线a、小回线和最大回线b. 回线中不同部分的三种磁化过程.6 -2 可

3、逆及不可逆磁化过程可逆及不可逆磁化过程 1、可逆及不可逆、可逆及不可逆DWD （1） 平衡条件和RDWD H=0时，畴壁按总自由能最低分布. 时, 畴壁位移到总自由能最小的平衡位置.0Hmin.UUiH0EEUUiHiHdV.dVEdVEoriHMKexiEEEEEEGenerally,a、等效外压力一畴壁在外场H下处于平衡状态下的畴壁元面积 , 设有一从j到k的虚位移 , 导致在体积元 中的磁化方向变化及外场作用能变化jkSx, xSvjkjkjkjksHvHMU)cos(cos)cos(coskjsjkHeHMUP对180畴壁, 令 kj,cos2seHMP 正的Pe 方向为从j指向k .

4、b、DWD的内部阻滞力jkjkiUPDWD导致在 内Ms从一个易轴方向k转到另一个易轴方向j. 对无缺陷的理想单晶体, ; 在实际晶体中, 由于缺陷导致 波动, 使得 . 为畴壁位置的函数.jk0iP0iPjkUc、畴壁平衡方程iePPeP为减小磁场作用能UH, 是畴壁位移发生的驱动力随H变化, 畴壁的平衡位置发生变化, 导致RDWD及磁化变化.jkUd、可逆磁化率 r (RDWD) 当H增加 , 畴壁移动 ,HxxdxdPPieHdxdPMdxdPPxikjsiecoscosHdSdxdPMxdSMMjkikjsjkkjsjk22coscoscoscos,iePP由kjjkHMMkjiikk

5、jsHrdxdPdSMHM)cos(cos22r为各向异性, 与畴壁面积S成正比,与 成反比, 依赖于能量Ei的起伏dxdPie. RDWD的特点畴壁为连续的较小的移动. M当外场变化 很小时, 磁化强度变化 可以趋近无穷小 H（2） 不可逆 DWD Pi 在材料中有起伏.当畴壁移动到b时, 畴壁处于不稳定平衡, 任何Pe或Pi的瞬时涨落, 可能导致畴壁发生一巨大的非连续性的跳跃过程, 直到在a和c之间的新的平衡位置.,maxiiPP 磁场H降低时,畴壁不会沿原路线跳回, 而是沿斜线变化, 直到加反向场才有可能发生反向跳跃. )cos(cosmax0kjsiMPH对180 DWDcos2max

6、0siMPH,cos10Hmax0iPH DWD 是连续的RDWD和不连续的IRDWD相间进行的.IRDWD的特点: 非连续性, 大的跳跃即使在 无穷小 H附近为磁化曲线最陡的部分.0H发生IRDWD的临界场为 Barkhausen跳跃2、可逆及不可逆磁畴转动、可逆及不可逆磁畴转动（1）外场H的扭矩导致畴中磁化转动总自由能 最低, 和 定义为 在极坐标中的角度.),(EsM, 0E0E, 022E022EHKEEEE（2） 以铁形晶体为例. H / (忽略E)110,cos1cos24221sHKHMKEEE, 0ddEor ,ddEddEKHiHLLsHMKcos1cos2221,cossM

7、M .12221sssHMMMMMK 依据 , 022dEdA至E为能量极小. RDR.cHH由当E至F为能量极大. 在 HC, a、 RDR 如果Ms原来沿110方向,当H减小至0时).(2点DMMs当H增加时, M增加并沿DCBA变化, 到B点饱和 BA 为水平线 .sMM .21ssMKH .022dEdcHH由当L至F为能量极小. RDR.1cos612212KMdHdMsr 当 , 0H124KMSirb、 IRDR and cH当H从 减小时, M从A到E可逆地减小 . 同样地, 当 H从 增加时, M从L到F可逆地变化, 在这些过程中均为能量极小. 而在从E到F一段, 为能量极大

8、cH原理如图所示. 在E和F , , 开始在 HC处出现不可逆转动.022dEdsaturationDRIRDRRDRR3、初始磁化率、初始磁化率 iRiwiDR 过程对具有高 的软磁材料 .iRiWi 对高频铁氧体, iRiKMsiR2ii4、高场磁化曲线、高场磁化曲线, 趋近饱和律趋近饱和律高场磁化曲线包含RDWD和RDR的末尾过程, 以及顺行磁化部分. （1） 趋近饱和律 . HHaHaMMps 2211i比较 的理论计算结果与实验结果, 可以判断 的机理. a. 极高场极高场 HMMpssM0Hp ， 可外推至 获得. 可由实验测定. b. 较高场较高场or 11HaMMs1aMMMM

9、HMssc. 中等高场中等高场 , 122HaMMsMs 和 a2 可由实验测定d. 利用计算机对高场磁化曲线拟合利用计算机对高场磁化曲线拟合, 可确定可确定a1, a2, p 和和 MS .( 2 ) 的来源. DR过程的最后阶段.22Ha 当 很小时 , sin0sKHMEE0EEEiKsLEEHMLsin 当H沿一般方向时 0EEK仅当 时 趋近于0 H 2121cos2HbMMMMsss222sKMEEb对立方晶体的无织构多晶材料 21112100222212122322535005811551610581KKKKMbas 如果 , Ki 可由 得到. 此外, 的确定也可以用于研究内应

10、力21, KKis2a2a.在多晶体中可通过 曲线观察到. 0KEsHsHHdHMdnn( 3 ) 奇点检测 当H沿晶体对称轴时, . 存在有限的饱和场 .样品磁化曲线在 处出现奇点. 饱和场或各向异性场可由此精确测定HdHMd22对单轴晶体的 RE-TM 合金.( 4 ) 项 . DWD的最后部分.1a 来源于缺陷 : 内应力, 位错, 杂质等, 这些因素使得饱和磁化难于达到. 1a( 5 ) , 铁磁态中的顺磁磁化率.HpHTp自旋波理论: 对巡游铁磁模型 00 p. When , .0T0pdLvvsdpaulip,局域模型.6-3 反磁化过程1. 反磁化的两种过程和矫顽力的三种机理(1

11、)两种过程a. DR: RDR 和IRDR. b. DWD: 反向畴成核, RDWD 和 IRDWD. (2)磁化反转及矫顽力的三个关键机制a.H0R of IDR, HC=H0R, 对单畴材料.b.Hn, 反向畴成核场.c.H0W : IRDWD的临界场.d.If Hn H0, HC= Hn. If H0 Hn, HC= H0.2. 单畴颗粒的DR及其HCEK为各种各向异性能对单轴各向异性: 磁晶各向异性能, 磁弹性能以及形状各向异性能等.( 1 ) 均匀转动均匀转动, 0)(HKEEEcos)(sin002sHMKEor ,1uKK or , 23s2)(21sLSMNN 0ddE0sin

12、)(2sin00sHMKcossMM 对单轴各向异性 (磁晶各向异性能 or/and 磁弹性能 or/and 形状各向异性能)a.特殊情况, 000sincossin20sHMKE0)cos2(sin0sHMK Solution 1:, 0sin, 0cos2cos2022sHMKdEd when ,201scMKHH0 when ,cHH is min. is energy min. Solution 2:KHMs2cos0,or ,220KHMMs1cosKKMHdEds22222022 when sMKH020 EMaxE when sMKH02, 0 EscMkH02sRMMsMMcH

13、cHHl 一般情况 , 005磁化反转 : DR+IRDR. 和 随 增加而减小 当 时, 随 增加而减小 当 时, 随 增加而增加, 但 在减小RMcH00H4000H040cH20, 0cH,20ssMKH ,0RMc.对取向混乱的单轴的单畴颗粒集合体,2479. 00scMKHsRMM5 . 0,64. 001scMKHsRMM832. 0对混乱取向的三轴单畴颗粒集合体无回线.d. 结论 单轴的单畴颗粒具有高的HC , 可达 . 较大的K可导致较高的HC. 具有最高HC的为有高度织构的集合体,其易轴与H平行. 一个单畴永磁体需要高的单轴各向异性, 高的TC 及室温下高的Ms. sMK2(

14、 2 ) 非均匀转动非均匀转动 细长单畴颗粒中的非均匀IDR具有较小的 .cHa 均匀DR a 球链模型的均匀转动.b. 球链模型的扭旋式. 退磁能减小.b. 椭球体中的扭旋式转动. 退磁能降低, 交换能增加.c.椭球体中的涡旋式转动. 退磁能降低, 交换能增加.非均匀DR过程导致的Hc依赖于颗粒尺寸.sccMHh20RRr sMAR2/ 10对无限长圆柱,有( 3 ) Hc 对颗粒尺寸的依赖关系对颗粒尺寸的依赖关系 多畴, M通过IRDWD反转, HC相对较低, 缺陷可增加HC 单畴 , , 非均匀转动. :critDD critcritDDdcHD ,:critDD ,thdD ,D,cH

15、热激发有助于M反转.,spdD 0cH23)(1DdHHspcoc当 critthdDd均匀转动, HC达极大值.( 4 ) 超顺磁性超顺磁性 .KVU 当V很小时, 热运动能kT接近于KV,kT可能Ms在易磁化轴不同方向的变化, 提供磁化反转的可能性, 和正常的顺磁性类似, 但单畴颗粒的磁矩为MsV, 远大于顺磁行为的原子磁矩. 剩磁的弛豫时间一个体积为V的单轴各向异性的单畴颗粒的势垒为,1kTKVef tRReMtM0)( :磁化反转运动频率fHz. 10102109sKMKHf对单畴颗粒, 若 , 在,以及 时, , 若 ,36/10cmergK KT300nmD4 . 3sec101n

16、mD4 . 4sec108spD , and ,spDD0RM0cH Dsp 依赖于温度T, 若测量时间为sec,100阻塞温度.25kTKV .25kKVTB 对 , Fe: ; Co: KTB300nmDsp5 .12.4nmDsp 与顺磁性类似, 单畴颗粒集合的磁化曲线可由下式给出 LCothMMs1kTHVMs注意单畴颗粒的磁矩MsV远大于原子磁矩3. 畴壁过程的磁化反转畴壁过程的磁化反转 ( 1 ) 理想饱和理想饱和: 无DW. 因此 反转需要sMa.出现反向磁化畴)(nHH b. IRDWD , 0HH c. When , ; When , ; 如何区分两种情况? 比较初始 曲线与

17、磁滞回线.0HHnncHH 0HHn0 HHcHM Hn: 成核场成核型钉扎型比较初始磁化曲线与磁滞回线0HHn0HHn( 2 ) 成核场成核场KnHH WnHH00nHa.在反磁化核中Ms反转180o. 对理想晶体,应有 在实验上 , . 为什么 ?,20snMKHwssnHMMKH02snMKH02为何 ?甚至 及 ? b. 解释来源于缺陷 () 缺陷处小的各向异性场KsMK02() 局域退磁场 MNLHeffM() 多晶中晶粒易磁化方向与外场不一致 ,20sMK.20KsMK在实际材料中的成核场seffpksnMNMKH02nH 可以小于平均的 !20sMK0nH 可能 , 成核现象出现

18、在第二象限.0nH甚至 , 成核出现在第一象限.4 . 剩磁及磁滞回线形状剩磁及磁滞回线形状MMMsR当外场从Hs降到0时, M从MS降到MRa. 设 在均匀外场下,cossMM : H与最近的易磁化轴的夹角(1) 剩磁剩磁( i ) 对简单单轴各向异性单晶或高织构多晶, 及强感生各向异性材料当 , . ./ aeH; 1SRMM.aeH0SRMM, 0nH( ii ) 非织构多晶 单轴晶体: 如Co, BaM, RE-TM.铁型晶体 : 镍型晶体 : 内应力可能导致降低 ,21dsincos20SRMM,831. 0cosSRMM.866. 0SRMM.SRMM0nH.SRMMb. 极大降低

19、极大降低 ( 2 ) 磁滞回线形状磁滞回线形状. 0RMc. 立方对称性: 较为复杂.d. 多晶体: 平均效应, 依赖于织构情况.e. 无外加场退火, 细腰型回线.a. 单轴各向异性: 磁场或应力退火, 当He.a., HnHw00, 方形回线 MRMs. 当 He.a., 回线倾向于直线,b. 织构材料. 与上类似i. 单畴颗粒及纳米线当H / e.a时,矩形回线, Hc=HK. Hc随角度偏离而减小. 当He.ae.a时时, ,回线基本为直线,H Hs s=H=HK K. .当测量方向稍偏离法线方向时, ,回线具有一较小的Hc 及较模糊的Hs. Hc随角度偏离而增加.e. 颗粒及线ii.

20、大颗粒及线 如果M通过畴壁位移反转, 回线形状可能依赖于不同因素有各种各样. 如果MR异常小, Hn 可能为负值.6 -4. 固体缺陷及对技术磁化影响固体缺陷及对技术磁化影响1. 缺陷及与磁化的相互作用 ( 1 ) 点缺陷点缺陷 : 原子空位, 杂质原子(替代型及空隙型 ) 线缺陷线缺陷: 位错 ; 面缺陷面缺陷 : 晶界 , 表面 , 层错 , 反相畴界面, 巨观缺陷巨观缺陷: (沉淀物 , 空洞, 缝隙).( 2 ) 与磁化的相互作用与磁化的相互作用 相关能量 , , , , and exEKEEME.HE两类相互作用.a. 长程作用长程作用.(i) 应力场 : 通过磁弹性相互作用 . 对

21、直线位错 , . 位错偶极子 , . 点缺陷应力场 , .r121r31r(ii) 局部退磁场(散磁场), 局域且非均匀. b. 短程作用短程作用. 在点缺陷,层错及面缺陷, 在缺陷位置局部 , , 发生局域变化.c.对软磁材料, 畴壁较宽 , 长程作用较为重要,短程作用常可略去. d. 非常硬的磁性材料(如RE+TM合金). 具有较高的K及较窄的畴壁. 短程作用更为重要AKsnm102. 早期的模型早期的模型, 内应力和掺杂理论内应力和掺杂理论( 1 ) 内应力理论内应力理论. 描述内应力起伏对畴壁移动的阻滞作用.a.低弥散度内应力低弥散度内应力 (i) 内应力不变号,但强度有起伏 . l,

22、180 DWForbkxAas)(23dxdpHMpisecos20,2sin2)(00lxx l: 波长 ,:20 振幅.当H=0时, 180DW出现在能量极小处 . 0dxddxdpHMxis/cos20DxHMsi1cos2cos2/max0siMpH DlMxssi1cos3402022lMHss000cos43l(ii) 符号变化的内应力起伏. DW. , DW 出现在 .o90lxsin00DlMxss1cos34200220b. 高弥散度内应力高弥散度内应力 . )(lo90020143xchls000cos3 . 0lMHss0066. 0 x钉扎.c.结论结论. , ) i

23、(2siMD1 , 10s , cos ) ii (2i,20l,1 ) iii (0iH. ) (ivl: 最大的阻滞效应, 低 i, 高0H,or 02l( 2 ) 掺杂理论掺杂理论a. 三种可能影响三种可能影响 .(i) DW中穿洞, 改变DW的面积及能量 .(ii) 出现磁荷分布,退磁能随畴壁位置改变.(iii) 出现次级畴 b.两种DWD(i) 平面DW.(ii) 弯曲 DW.b. 低弥散度掺杂， (i) 球状掺杂颗粒, 直径为d , 间距为l的简立方分布. 180 平面DW. 当平面DW通过掺杂且离球心为x时, 一个单胞上DW面积为d, 4222xdls2221cos2lxdxds

24、lpHMpise32022232cos621dKMsi36ld, 掺杂体积分数.,cos6232320dMKHsd(ii) 片状掺杂 spMcH20c.高弥散度掺杂高弥散度掺杂d,2602230 xchKld,cos61232202232dKMsid320320cos639dMKHs最大效应发生在 d(3) 弥散退磁场理论弥散退磁场理论不均匀应力及掺杂造成体磁荷分布和弥散的退磁场不均匀应力及掺杂造成体磁荷分布和弥散的退磁场. 能量依赖于畴壁的位置及畴壁位移.内应力: 21206 . 4log39. 105. 1isssisMMH: 不均匀应力影响区域的体积分数.掺杂 : 21202log213

25、9. 02KMMKHss: 掺杂的体积分数.)K High ( 3601 . 2 :Fe0HHc) high ( 97330 : Nis0HHc3. 缺陷与磁化相互作用的精确理论缺陷与磁化相互作用的精确理论 ( 1 ) 位错位错位错与磁化间相互作用主要通过磁弹性效应.a. 位错位错畴壁畴壁(i) 基本计算. 畴壁能在位错应力场中变化，受力pw. 相应的，位错处于畴壁的应力场中，受到作用力pd.wMdpbsdp ds : 位错包围面积的面积元.: 畴壁产生的应力张量.M: Bergers矢量. b由Stokes定理 bl dpMddl : 位错线元.基于上式方程, 位错对DWD产生阻滞力， 和

26、能由之计算得到。icH(ii) 两类DW. a.第一类, 如180oDW, 应力基本局限在畴壁内. 仅当畴壁穿过位错时相互作用才存在.因此180oDW易于移动.b. 第二类, 如90oDW, 应力延伸到畴壁之外，较长程. 这类畴壁与晶体中所有位错均有相互作用. 因此90DW难于移动,需要较高磁场.b. 位错及其他局部缺陷对均匀磁化的影响位错及其他局部缺陷对均匀磁化的影响. () 分布在畴内或整个晶体内的均匀磁化在位错及其他缺陷邻近可能受到扰动（由于磁弹性作用）. 局域磁化的非均匀可由下式求得0MHkexEEEEE() 交换长度 在位错或其他缺陷中心处的磁化偏离由易磁化方向或高场下的磁化方向决定

27、的平均方向. 交换作用阻止Ms方向的突变，使得磁化方向在一定的扩展区域内逐渐变化（类似畴壁）。交换长度描述缺陷邻近非均匀的范围.sMexlsM212sHHMAl高场近饱和区的交换长度.21KAlK畴的交换长度（磁晶各向异性）. 2122sMMAl考虑到磁化偏离能量的交换长度. ( 2 ) 点缺陷点缺陷 异质原子, 空穴及微小杂质等a.异质原子的局域作用能fffiifiiffSLSiLSSJE2212/1500/ )(/ )(1exfexkfksaaaaMH导致 A, K, Ms 等的变化.( 3 ) 面缺陷面缺陷a. 晶界,表面,堆垛层错,反相界, 片状脱溶体.b. 与畴壁相互作用的计算. 设

28、面缺陷厚度为D.12xxDD2211,xxdxHMKdxdAisiicossin022当 时, 畴壁的能量可以被分成三个部分,.3,2,1i 每个区域内进行变分处理.0sincossin22 siiHMKA在不同区域：,31AAA,31KKK,2AAKK2边界条件: 00dxd0dxd在区域间边界处 .constdxdAiEuler方程:12KKAADMKHs00依据=min.条件, 可求得 和 随H而变化, 即畴壁位置随H而移动. 最大的H为注意缺陷引起的畴壁中 分布的变化.虚线为未受缺陷扰动的自旋分布. 实线为缺陷影响示意. ( 4 ) 缺陷与反磁化畴成核场缺陷与反磁化畴成核场 a.各种缺

29、陷阻止畴壁移动并且导致高场下难于饱和。另一方面, 缺陷可帮助反向畴成核 降低成核场. 没有被强场完全去除的在缺陷处的残留磁畴可能是反向畴的潜在成核位置b. 空泡、非磁性掺杂以及脱溶体等可能成为高Ms材料反向畴的核.(i) 具有矩形回线的环状permivar合金样品.表面刻痕可降低Hc 虚线: 正常测量实验证据实验证据 实线: 迅速将反向场降低至适当值, 反磁化仍可继续进行在cHH 0(ii) 下图显示了随H从 在第一象限内降低时, 硅钢晶体缺陷附近钉状畴的观测情况. 残留的钉状畴(90o)随H降低逐渐长大并产生一个180o的反转畴.sHH c. 面缺陷对成核效应的更多影响面缺陷对成核效应的更多影响() 晶界上的剑状畴 晶界上一个剑状畴的能量变化coscos22122nppssMNMEEVHMVNMsDEEE2D: 产生剑状畴的晶界面积ME 和