第3章控制工程ppt控制系统的时域分析-V1.1

1、 时域分析法时域分析法是研究控制系统在输入信号作用下，其输出随是研究控制系统在输入信号作用下，其输出随时间变化的情况，方便分析系统的动态和稳态特性，是控制时间变化的情况，方便分析系统的动态和稳态特性，是控制系统最基本的分析方法，也是频域分析法和根轨迹分析法的系统最基本的分析方法，也是频域分析法和根轨迹分析法的基础。基础。时域分析包括稳定性分析、瞬态性能分析和稳态性能分析。时域分析包括稳定性分析、瞬态性能分析和稳态性能分析。解解表达式表达式曲曲 线线系统性能系统性能稳定性稳定性快速性快速性稳态精度稳态精度分析分析拉氏变换拉氏变换微方微方第第3 3章章 控制系统的时域分析控制系统的时域分析 3.1

2、 3.1 响应分析响应分析3.1 时域分析有关概念时域分析有关概念 时域分析是指分析控制系统在典型输入信号作用下的输出响应，时域分析是指分析控制系统在典型输入信号作用下的输出响应，根据输出的时域表达式，分析系统的稳定性、瞬态和稳态性能。根据输出的时域表达式，分析系统的稳定性、瞬态和稳态性能。时域分析法具有以下特点：时域分析法具有以下特点： (1)由于时域分析是直接在时间域中对系统进行分析的方法，所由于时域分析是直接在时间域中对系统进行分析的方法，所以时域分析以时域分析具有直观和准确的优点具有直观和准确的优点； (2)可以可以从响应表达式或曲线上得到系统时间响应从响应表达式或曲线上得到系统时间响

3、应的全部信息；的全部信息； (3)时域分析采用的是解析方法，过程较为繁琐；时域分析采用的是解析方法，过程较为繁琐； (4)难于判断系统的结构和参数对动态性能的影响，进行系统设难于判断系统的结构和参数对动态性能的影响，进行系统设计时一般不用时域分析法；计时一般不用时域分析法； (5)对高阶系统进行分析时计算量很大，不易确定性能指标，必对高阶系统进行分析时计算量很大，不易确定性能指标，必须借助于计算机实现。须借助于计算机实现。3.1.1 时域分析常用的方法时域分析常用的方法 时域时域稳定性分析稳定性分析采用的是代数判据，即采用的是代数判据，即劳斯稳定性判据和赫劳斯稳定性判据和赫尔维兹稳定性判据尔维

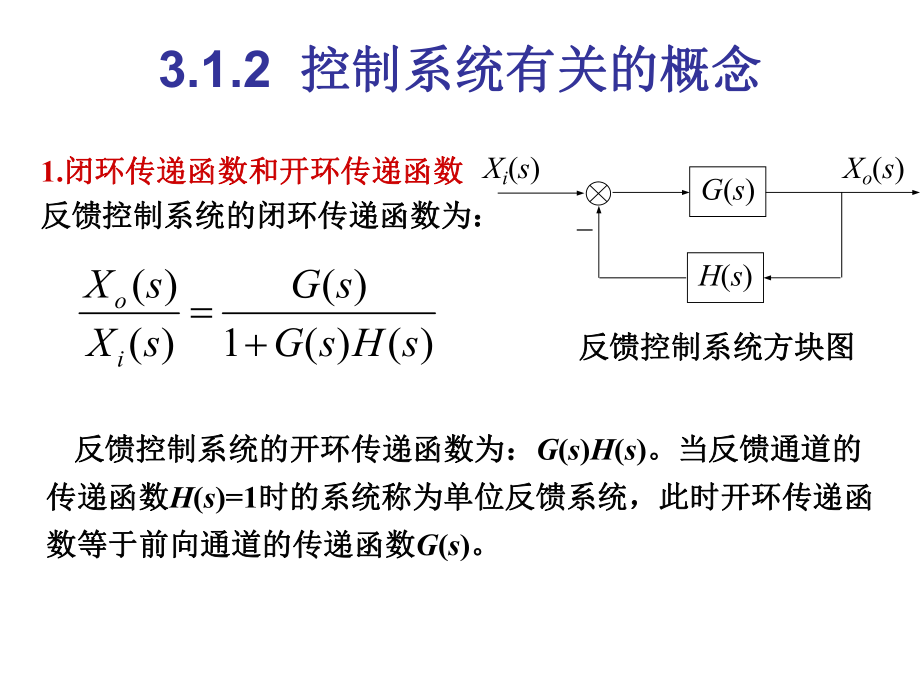
4、兹稳定性判据；稳态性能分析稳态性能分析就是通过计算就是通过计算稳态误差稳态误差来来分析系统的准确性；时域响应分析采用的方法有两种，一是分析系统的准确性；时域响应分析采用的方法有两种，一是直接由微分方程求解得出，二是由传递函数采用拉氏反变换直接由微分方程求解得出，二是由传递函数采用拉氏反变换的方法求出。的方法求出。输入信号输入信号xi(t)象函数象函数Xi(s)Xo(s)= G(s) Xi(s)输出的时域表达式输出的时域表达式xo(t)3.1.2 控制系统有关的概念控制系统有关的概念Xi(s)G(s)H(s)_Xo(s) 反馈控制系统方块图反馈控制系统方块图1.闭环传递函数和开环传递函数闭环传递

5、函数和开环传递函数反馈控制系统的闭环传递函数为：反馈控制系统的闭环传递函数为：)()(1)()()(sHsGsGsXsXio反馈控制系统的开环传递函数为：反馈控制系统的开环传递函数为：G(s)H(s)。当反馈通道的。当反馈通道的传递函数传递函数H(s)=1时的系统称为单位反馈系统，此时开环传递函时的系统称为单位反馈系统，此时开环传递函数等于前向通道的传递函数数等于前向通道的传递函数G(s)。2.特征方程和特征根特征方程和特征根控制系统的闭环传递函数一般可以写成如下分式多项式的形式：)()()()(11101110sDsMasasasabsbsbsbsXsXnnnnmmmmio对于实际存在的控制

6、系统，满足nm。系统的特征方程特征方程是闭环传递的分母多项式D(s)等于0所对应的方程，即D(s)=a0sn+a1sn-1+an-1s+an=0。特征方程的根，即D(s)=0的解，称为系统的特征根特征根。32)2(2)()(2ssssXsXio220ReIm-1-2图3.1.2 系统零极点分布图3.系统的零点、极点和零极点分布图系统的零点、极点和零极点分布图 零点和极点分开环零极点和闭环零极点。闭环传递函数中，分子多项式对应的方程M(s)= 0的解，称为系统的闭环零点闭环零点；分母多项式对应的方程D(s)=0的解称为系统的闭闭环极点环极点，可见闭环极点与系统的特征根等价。开环传递函数的分子多项

7、式等于0的所对应的方程的解称为系统的开环零点开环零点，开环传递函数分母多项式等于0的所对应的方程的解称为系统的开环极点开环极点。所谓零极点分布图零极点分布图就是在s平面上，把系统的零点和极点所对应的矢量的端点标注出来，零点用“”表示，极点用“”表示。若系统的传递函数为4.开环增益和根轨迹增益开环增益和根轨迹增益设反馈控制系统的开环传递函数G(s)H(s)可以写成如下标准形式：111111)()(2121sTsTsTssssKsHsGnm其中0，1，2，m，T1，T2，Tn-均为大于0的时间常数，则分子多项式中的常数K称为开环增益称为开环增益。 若开环传递函数又写成如下标准形式：nmpspsps

8、szszszsKsHsG2121*)()(K*称为开环根轨迹增益。z1，z2，zm为系统的开环零点；p1，p2，pn-为系统的开环极点。开环增益和根轨迹增益可以进行相互转化，二者的关系是：nmTTTKK2121*3.1.3 典型输入信号典型输入信号 时域响应表现了系统的动态性能。不仅取决于系统时域响应表现了系统的动态性能。不仅取决于系统本身特性（微方），还与输入信号形式有关。本身特性（微方），还与输入信号形式有关。 系统工作时，外加输入信号是随机的，系统分析和系统工作时，外加输入信号是随机的，系统分析和设计时，对各种系统性能进行比较要预先规定一些具有设计时，对各种系统性能进行比较要预先规定一些

9、具有特殊形式的实验信号作为输入，然后比较系统的响应。特殊形式的实验信号作为输入，然后比较系统的响应。 sXi sXo s sXsLsXLtxsXssXiooio11规定一些特殊的试验输入信号各种系统比较各种系统对这些试验信号的响应典型信号的选取原则典型信号的选取原则输入的形式应反映系统在工作中所响应的实际输入；输入的形式应反映系统在工作中所响应的实际输入；输入信号在形式上应尽可能简单，以便于对系统响应输入信号在形式上应尽可能简单，以便于对系统响应的分析；的分析；应选取能使系统工作在最不利情况下的输入信号作为应选取能使系统工作在最不利情况下的输入信号作为典型输入信号。典型输入信号。 常用的典型实

10、验信号常用的典型实验信号 阶跃阶跃、斜坡、抛物线、脉冲、斜坡、抛物线、脉冲 正弦（频率分析法）正弦（频率分析法）1. 阶跃函数阶跃函数 阶跃函数的拉普拉斯变换为阶跃函数的拉普拉斯变换为00( )0tr tAt，( )AL Ats为单位阶跃函数。为单位阶跃函数。时，时，为常数，当为常数，当其中其中1 AA2. 斜坡函数斜坡函数 斜坡函数的拉普拉斯变换为斜坡函数的拉普拉斯变换为2( )BL tts00( )0tr tBtt，为单位斜坡函数。为单位斜坡函数。时，时，为常数，当为常数，当其中其中1 BB3.加速度函数（抛物线函数抛物线函数）拉普拉斯变换为拉普拉斯变换为200( )102tr tCtt，

11、231( )2CLCtts称称为为单单位位加加速速度度函函数数。时时，为为常常数数，当当其其中中1 CC4. 脉冲函数脉冲函数 理想脉冲函数的拉普拉斯变换为理想脉冲函数的拉普拉斯变换为00( )0tthr tAthh ，或， 其中脉冲宽度为其中脉冲宽度为h，脉冲面积等于脉冲面积等于A，若对脉冲的宽度若对脉冲的宽度h取趋于取趋于零的极限，则有零的极限，则有 000)(tttr， Adttr )(当当A=1（ h 0）时，称此脉冲函数为理想单位脉冲函数，记作）时，称此脉冲函数为理想单位脉冲函数，记作 。 )(t ( )1Lt t05. 正弦函数正弦函数 正弦函数的拉普拉斯变换为正弦函数的拉普拉斯变

12、换为22sinAL Ats( )sinr tAt正弦信号在时域分析中一般不用，主要用于频域分析。正弦信号在时域分析中一般不用，主要用于频域分析。究竟采用哪种典型信号？取决于系统在正常工作情况下最常见的输入信号 形式。斜坡信号 随时间逐渐变化的输入阶跃信号 突然的扰动量、突变的输入脉冲信号 冲击输入正弦信号 随时间往复变化的输入 3.1.4 控制系统的时域响应及性能指标控制系统的时域响应及性能指标 1. 动态动态响应响应：又称为过渡过程或瞬态响应（过程），是：又称为过渡过程或瞬态响应（过程），是指系指系统在典型输入信号作用下，系统输出量从初始状态到接近统在典型输入信号作用下，系统输出量从初始状态

13、到接近最终状态的响应过程最终状态的响应过程。2. 稳态响应：是稳态响应：是系统在典型输入信号作用下，当时间系统在典型输入信号作用下，当时间t趋于趋于无穷时，系统输出量的表现方式无穷时，系统输出量的表现方式。稳态响应又称稳态过程，。稳态响应又称稳态过程，表征系统输出量最终复现输入量的程度，用稳态误差来描表征系统输出量最终复现输入量的程度，用稳态误差来描述。述。一、控制系统的时域响应一、控制系统的时域响应稳态响应稳态响应瞬态响应瞬态响应t txo txi二、控制系统的时域性能指标二、控制系统的时域性能指标 时域性能指标包括动态性能指标和稳态性能指标两种。时域性能指标包括动态性能指标和稳态性能指标两

14、种。动态性能指标动态性能指标是描述控制系统在典型信号输入是描述控制系统在典型信号输入(一般都用单位一般都用单位阶跃信号阶跃信号)作用下的过渡过程的性能指标，常用的动态性能指作用下的过渡过程的性能指标，常用的动态性能指标有上升时间、峰值时间、调整时间、超调量和振荡次数等标有上升时间、峰值时间、调整时间、超调量和振荡次数等几种。几种。响应曲线从0上升到稳态值的100%所用时间rt响应曲线达到第一个峰值所用时间pt在响应曲线的稳态值上，用稳态值的绝对百分数做一个允许误差范围，响应曲线达到并且永远保持在这一允许误差范围内所用的最小时间st10ttxopM %100oopoxxtx这些点已被确定0.05

15、或0.02超调系统超调系统 txo(t)xo()误差tsABCDtr0.9xo()0.1xo()响应曲线从稳态值的10%上升到稳态值的90%所用时间无超调系统无超调系统（1）上升时间）上升时间tr 响应曲线从零时刻到首次到达稳态值的时间，或：响响应曲线从零时刻到首次到达稳态值的时间，或：响应曲线从稳态值的应曲线从稳态值的10%上升到上升到90%所需时间（无超调系统）所需时间（无超调系统）反映响应曲线上升趋势表示响应速度指标。反映响应曲线上升趋势表示响应速度指标。（2）峰值时间）峰值时间tp 响应曲线从响应曲线从0到达第一个峰值所需的时间。到达第一个峰值所需的时间。（3）调整时间（调节时间）调整

16、时间（调节时间）ts 在响应曲线从在响应曲线从0到达且不再超过稳态值的到达且不再超过稳态值的5%或或2%误差范围所需的最少时间。（允许误差误差范围所需的最少时间。（允许误差=0.05或或= 0.02）（4）最大超调量最大超调量% 指在系统响应过程中，输出量的最大值超过稳态值的百指在系统响应过程中，输出量的最大值超过稳态值的百分比分比 （5）振荡次数）振荡次数N：在调节时间：在调节时间ts内，内，c(t)偏离偏离c()的振荡次数。的振荡次数。( )( )%100%( )pc tcc稳态性能指标稳态性能指标用稳态误差表示，是系统的控制精度的一种度用稳态误差表示，是系统的控制精度的一种度量，通常在阶

17、跃信号、斜坡信号和加速度信号作用下进行测量，通常在阶跃信号、斜坡信号和加速度信号作用下进行测定或计算。在稳态定或计算。在稳态(时间趋于无穷大时间趋于无穷大)时，如果系统的输出量不时，如果系统的输出量不等于输入量或输入量的函数，则说明系统存在误差。等于输入量或输入量的函数，则说明系统存在误差。注：注： 上升时间、峰值时间和调节时间都表示动态过程进行的快慢程度，上升时间、峰值时间和调节时间都表示动态过程进行的快慢程度，是是快速性指标快速性指标。超调量反映动态过程振荡激烈程度，是超调量反映动态过程振荡激烈程度，是平稳性指标平稳性指标，也称相对稳，也称相对稳定性能。定性能。超调量和调节时间是反映系统动

18、态性能好坏的两个最主要指标。超调量和调节时间是反映系统动态性能好坏的两个最主要指标。而稳态误差反映了而稳态误差反映了系统的准确性系统的准确性。一般来说，对于控制系统我们总希望具有平稳、准确和快速的性一般来说，对于控制系统我们总希望具有平稳、准确和快速的性能，也就是希望超调量小一些，振荡次数少一点，调整时间短一能，也就是希望超调量小一些，振荡次数少一点，调整时间短一些，稳态误差小一些。但在后面的学习过程中就会发现，这些性些，稳态误差小一些。但在后面的学习过程中就会发现，这些性能往往相互矛盾，只能针对具体的系统而有所侧重。能往往相互矛盾，只能针对具体的系统而有所侧重。3.2 稳定性分析稳定性分析3

19、.2.1 稳定的概念及稳定的充分必要条件稳定的概念及稳定的充分必要条件 一、稳定的基本概念一、稳定的基本概念 一个系统受到扰动，偏离了原来的平衡状态：一个系统受到扰动，偏离了原来的平衡状态：当扰动取消后，这个系统又能当扰动取消后，这个系统又能够逐渐恢复到原来的状态。够逐渐恢复到原来的状态。稳定稳定 不稳定不稳定扰动取消后，系统不能扰动取消后，系统不能恢复到原来的状态。恢复到原来的状态。Mbcoodfabcde条件稳定系统b、c允许偏差范围d、e规定偏差边界稳定系统不稳定系统控制系统的稳定性的另一种定义：控制系统的稳定性的另一种定义：若控制系统在任何足够小的初始偏差若控制系统在任何足够小的初始偏

20、差作用下，其过渡过程随着时间的推移，作用下，其过渡过程随着时间的推移，逐渐衰减并趋于零，具有恢复原平衡逐渐衰减并趋于零，具有恢复原平衡状态的性能，则称该状态的性能，则称该。否则，。否则，称该称该。 控制理论中所讨论的稳定性控制理论中所讨论的稳定性其实都是指其实都是指下的稳定性下的稳定性也就是讨论也就是讨论，仅存，仅存在在时的稳定性，即时的稳定性，即讨论自由振荡是讨论自由振荡是的还是的还是的。的。二、稳定的二、稳定的充分必要条件充分必要条件t tnt txit=0 txot 00iooxx- sG1 sG2 sXi sXo sN- sG1 sG2 sXi sXo sN sNbsbsbsbsXas

21、asasammmmonnnn11101110 nnnnmmmmoasasasabsbsbsbsGsGsGsNsX 111011102121 nnnnmmmmoasasasabsbsbsbsX11101110 ，等效成脉冲信号，干扰信号持续时间很短 11 cossinjikrttoijjjjijxtD eeEtFt 若系统稳定，则若系统稳定，则 0|otxt 00ij ，系统稳定的充要条件系统稳定的充要条件rjjjjjjjikiijsjsesdsc11)()(00 ji，件是：系统稳定的充分必要条若特征根中有一个或多个根具有若特征根中有一个或多个根具有正实部正实部，则零输入响应将随时间的推移而则

22、零输入响应将随时间的推移而发散发散，这，这样的系统就不稳定。样的系统就不稳定。 ij，对应闭环传递函数对应闭环传递函数特征根的特征根的若特征根的实部均为若特征根的实部均为负值负值，则零输入响应，则零输入响应将随时间的推移而将随时间的推移而收敛收敛，这样的系统就是，这样的系统就是稳定的。稳定的。 稳定性是控制系统自身的固有特性，它稳定性是控制系统自身的固有特性，它取决于系统本身的结构和参数，而与输取决于系统本身的结构和参数，而与输入入无关无关；对于纯线性系统来说，系统的；对于纯线性系统来说，系统的稳定与否并不与初始偏差的大小稳定与否并不与初始偏差的大小有关有关。 控制系统稳定的充分必要条件是：控

23、制系统稳定的充分必要条件是： 系统特征方程式的根全部具有系统特征方程式的根全部具有负实部负实部。闭环传递函数的极点全部具有负实部闭环传递函数的极点全部具有负实部（位于（位于左左半半s平面）。平面）。例例1系统的闭环传递函数如下，判断系系统的闭环传递函数如下，判断系统是否稳定？统是否稳定？5( )(1)(6)sG sss 稳定单位反馈系统的开环传递函数如下，单位反馈系统的开环传递函数如下，判断系统是否稳定？判断系统是否稳定？例例25( )(2)sG ss 不稳定对于一阶系统对于一阶系统，特征方程为，特征方程为D(s)=a0s+a1=0，特征根为，特征根为s=-a1/a0，只要，只要s 小于小于0

24、，则系统稳定。，则系统稳定。对于二阶系统对于二阶系统，特征方程为，特征方程为D(s)=a0s2+a1s+a2=0，对应，对应的特征根为的特征根为0202112, 124aaaaas只要只要a2，a1，a0都大于都大于0，则系统稳定。，则系统稳定。对于三阶以上的系统对于三阶以上的系统，要采取下面介绍的方法进行判断。，要采取下面介绍的方法进行判断。3.2.2 代数稳定判据代数稳定判据 为了避开对特征方程的直接求解，讨论为了避开对特征方程的直接求解，讨论特征根的分布特征根的分布，看其是否全部具有，看其是否全部具有负实部负实部，并以此来判断系统的稳定性。这就产生了一并以此来判断系统的稳定性。这就产生了

25、一系列系列稳定判据稳定判据。4325( )356sG ssss 一、劳斯判据一、劳斯判据稳定的稳定的必要必要条件：条件： 特征方程中各项系数特征方程中各项系数00 0122110 nnnnnasasasasasD系统特征方程为：系统特征方程为：稳定的稳定的充分充分条件：条件： 劳斯阵列劳斯阵列中第一列所有项中第一列所有项0？劳斯阵列如下：0123213n3212n75311n6420nssscccsbbbsaaaasaaaas 一直计算到最后一行算完一直计算到最后一行算完为止。然后判断阵列中第一列为止。然后判断阵列中第一列系数的符号，若全部系数的符号，若全部0,则系统则系统稳定；否则，第一列系

26、数稳定；否则，第一列系数符号符号改变的次数改变的次数，就为特征方程在，就为特征方程在右半右半s平面平面的的根数根数。130211aaaaab 150412aaaaab 170613aaaaab 121311bbaabc 131512bbaabc 0122110 nnnnnasasasasasD01234sss042s33s 1 判断系统稳定性判断系统稳定性、系统特征方程为：、系统特征方程为：例例 034321234 sssssD解：满足必要条件 13-23 系统不稳定。系统不稳定。个右根，个右根，有有次，次，符号改变符号改变劳斯阵列第一列劳斯阵列第一列22sD0 K必要条件：- sXi sXo

27、21sssK例例3K为何值时，系统稳定 K2s1ssK2s1ssK12s1ssKsXsXio 解：解： 02323 KssssD系统特征方程为：系统特征方程为：0123ssKs2s 3 1 3K6 K60 K 系统稳定的充要条件：0K0K60 有：有：符号符号满足劳斯阵列第一列满足劳斯阵列第一列劳斯判据的两种特殊情况：劳斯判据的两种特殊情况：1、某一行第一个元素为零，而、某一行第一个元素为零，而其余各元素均不为零、或部其余各元素均不为零、或部分不为零；分不为零；2、某一行所有元素均为零。、某一行所有元素均为零。01234s s s 2 1 s 4 2 1 s 判断系统稳定性：例 04s2s2s

28、ssD423442 第一列系数符号改变第一列系数符号改变两次，系统有两个右根，两次，系统有两个右根，所以，系统不稳定。所以，系统不稳定。404 判断系统稳定性判断系统稳定性：例例 02ss2ssD523 0123ssss 2 2 1 1 02第一列系数符号无改变，第一列系数符号无改变，故系统没有正实部的根。故系统没有正实部的根。 2, 02s122 s223 sjssssS 行为行为0， 表明系统有一对共表明系统有一对共轭虚根，所以，系统临界稳定。轭虚根，所以，系统临界稳定。 1s1s由该行的上一行元素来解决：由该行的上一行元素来解决：(1) 构成辅助多项式，并求导，用其系数代构成辅助多项式，

29、并求导，用其系数代替全为零的行；替全为零的行；(2) 可以利用辅助方程，解出这些特征根。可以利用辅助方程，解出这些特征根。2、某一行所有元素均为零、某一行所有元素均为零 表明在表明在 S S 平面内存在大小相等、符号相反平面内存在大小相等、符号相反的实根或共轭虚根的实根或共轭虚根S显然，这些根的显然，这些根的数目一定是偶数数目一定是偶数。 016s16s20s12s8s2ssD623456：例0123456sssssss 16 12 2 16 12 2 16 20 8 1 辅助多项式辅助多项式8624 ss 1 331 第一列符号全为正，第一列符号全为正，说明系统无右根，但有说明系统无右根，但

30、有共轭虚根，可由辅助方共轭虚根，可由辅助方程解出。程解出。辅助方程辅助方程08s6s24 3 8 8ss1243 求导：ss343 ：除以 04s2s22 2js2js4 . 32 . 1 1 6 80 0 系统临界稳定系统临界稳定二、利用劳斯判据看系统相对稳定性二、利用劳斯判据看系统相对稳定性 再再应应用用劳劳斯斯判判据据的的方方程程式式，代代入入系系统统特特征征式式，得得到到将将，令令向向左左平平移移虚虚轴轴zzssz S0若系统闭环特征根均在若系统闭环特征根均在s左半平面，且和虚左半平面，且和虚轴有一段距离，则系统有一定的稳定裕量轴有一段距离，则系统有一定的稳定裕量以以右右有有无无闭闭环

31、环特特征征根根平平面面试试判判断断系系统统在在 -s69 .156111720123ssss28 . 125120123zzzz例例3.2.9 系统的特征方程为系统的特征方程为D(s)= 2s3+11s2+17s+6=0，判断系统的，判断系统的稳定性，并确定特征根是否全位于稳定性，并确定特征根是否全位于s=-1线以左。线以左。解解 (1)列劳斯列表列劳斯列表劳斯列表第一列元素符号没有变化，因此，劳斯列表第一列元素符号没有变化，因此，系统稳定。系统稳定。(2)进行变量代换进行变量代换s=z-1，得新的特征方程，得新的特征方程D(z)= 2z3+5z2+z-2=0。特征方程的系数不全为。特征方程的

32、系数不全为正，所以有特征根不全在正，所以有特征根不全在z左半平面左半平面(s=-1线以线以左左)，继续列劳斯列表：，继续列劳斯列表：劳斯列表第一列元素符号变化一次，因此有劳斯列表第一列元素符号变化一次，因此有1个个特征根位于特征根位于s=-1线以右。线以右。 实际实际D(s)= 2s3+11s2+17s+6=2(s2+5s+6)( s+0.5)=0，特征根为，特征根为-2，-3和和-0.5，与劳斯判据的，与劳斯判据的结论一致。结论一致。 右边有没有闭环特征根平面的判断系统在例1-s 24s50s35s10s1s3 . 010000sXsX 10. 2 . 3234io 代代入入系系统统特特征征

33、式式，得得即即解解：令令1 ,1 zssz 0241501351101234 zzzz06116 234 zzzz即即不满足系统稳定的必要条件：不满足系统稳定的必要条件：特征方特征方程中各项系数程中各项系数0右右边边有有闭闭环环特特征征根根平平面面的的系系统统在在系系数数为为即即10 0 sz作业 3-1（1）（2）（3） 3-3 3-8传递函数传递函数( )1( )( )1C ssR sTs结构图结构图R(s)C(s)11Ts 1T sR(s)C(s)-3.3 3.3 一阶系统的时域分析一阶系统的时域分析 凡是用一阶微分方程描述的系统称为一阶系统，传递函数的分母凡是用一阶微分方程描述的系统称

34、为一阶系统，传递函数的分母多项式为多项式为1次多项式。次多项式。 3.3.1 一阶系统的单位阶跃响应一阶系统的单位阶跃响应1( )11111( )( )111C sR sTsTsssR sssT单单位位阶阶跃跃信信号号111( )1(0)1tTc tLetssT 特点：特点： 按指数规律上升按指数规律上升 t t=0=0处切线斜率为处切线斜率为1/1/T 100( )11tTttdc tedtTT参数未知，可由一阶系统单位阶跃响应实验参数未知，可由一阶系统单位阶跃响应实验曲线确定曲线确定T( )63% ( )tTc tc txoT 2T 3T 4T 5T98.2%95%99.3%86.5%B0

35、t163.2%A0.632一阶系统的单位阶跃响应曲线没没有有超超调调，非非周周期期响响应应，惯惯性性环环节节亦亦称称非非周周期期环环节节。调整时间调整时间ts理论上：瞬态结束进入稳态理论上：瞬态结束进入稳态 t工程上：与系统要求精度有关工程上：与系统要求精度有关 ts=4T (误差范围误差范围2%) ts=3T (误差范围误差范围5%） ts大小作为评价系统响应快慢的指标：调整系统参数大小作为评价系统响应快慢的指标：调整系统参数T提高系统快速性提高系统快速性 注：注：ts只反映系统特性，与输入、输出无关。只反映系统特性，与输入、输出无关。1/T1.00.20.40.60.80.630.870.

36、950.980.99T2T3T4T5Tc(t)t3.3.2 一阶系统的单位斜坡响应一阶系统的单位斜坡响应22211111( )( )111/( )TTC sR sTsTsR ssssssT单单位位斜斜坡坡信信号号( )()0t Tc ttTTet TeTTTtttxtxteeetTtToi 111(1)系统是稳定的。(2) xo()=t-T，稳态误差ess= xi(t)- xo()=T。一阶惯性环节跟踪斜坡输入信号时有误差，并且时间常数T越小，稳态误差越小，准确性越好。3.3.3 一阶系统的单位脉冲响应一阶系统的单位脉冲响应 1 sRttr tTtcetT111 111 TssRsRsCsCT

37、1sT1 98.2%95%99.3%86.5%B0tT 2T 3T 4T 5T txoT163.2%AT1368. 03.3.4 一阶系统的单位抛物线响应一阶系统的单位抛物线响应3223321111( )( )111/( )1TTTC sR sTsTsssssR sssT单单位位抛抛物物线线信信号号221( )(1)02t Tc ttTtTet当时间当时间t时，系统输出信号与输入信号时，系统输出信号与输入信号之差将趋于无穷大。说明对于一阶系统是之差将趋于无穷大。说明对于一阶系统是不能跟踪单位抛物线函数输入信号的。不能跟踪单位抛物线函数输入信号的。 221tr (t)c(t)（t） 1（t） t

38、 tTeT11tTe11)1 (1tTeTt)1(21122tTeTTtt1. 一阶系统对典型输入信号的响应及一阶系统对典型输入信号的响应及响应之间关系响应之间关系3.3.5 一阶系统的重要性质一阶系统的重要性质一阶系统只有一个特征参数一阶系统只有一个特征参数T，即其时间常数。在一定，即其时间常数。在一定的输入信号作用下，其时间响应的输入信号作用下，其时间响应c(t)由其时间常数惟一确由其时间常数惟一确定。定。 从表可以看出：系统对输入信号导数的响应等于系统对从表可以看出：系统对输入信号导数的响应等于系统对该输入信号响应的导数；系统对输入信号积分的响应等于该输入信号响应的导数；系统对输入信号积

39、分的响应等于系统对该输入信号响应的积分。这一重要特性适用于任何系统对该输入信号响应的积分。这一重要特性适用于任何阶次的线性定常系统阶次的线性定常系统线性定常系统的重要特性。线性定常系统的重要特性。 利用这一特点，在测试系统时，可以用一种信号输入推利用这一特点，在测试系统时，可以用一种信号输入推断出几种相应信号的响应结果，带来很大方便。而线性时断出几种相应信号的响应结果，带来很大方便。而线性时变系统和非线性系统都不具备这种特性。变系统和非线性系统都不具备这种特性。2. 结论结论例题例题1. 一阶系统的单位阶跃响应达稳态值的一阶系统的单位阶跃响应达稳态值的95%98%时，响应时间为时，响应时间为

40、答案：答案：34T 2111tx tte2.一阶系统的单位阶跃响应为 则此系统的脉冲响应为（ ） 221txtte答案：3. 一阶系统输入下列哪种信号会存在稳态一阶系统输入下列哪种信号会存在稳态误差（误差（ ）A.阶跃信号阶跃信号 B.脉冲信号脉冲信号 C. 斜坡信号斜坡信号C4. 系统的传递函数分别如下所示，则当输系统的传递函数分别如下所示，则当输入信号为单位阶跃信号时，系统（）的输入信号为单位阶跃信号时，系统（）的输出最先到达稳定状态。出最先到达稳定状态。( )1( )31sssoiXA. X( )2( )31sssoiXB. X( )2( )1sssoiXC. X( )1( )21sss

41、oiXD. XC1111111)()(sKKKKsKsKsKsXsXioKT11 . 0133KTXi(s)_Xo(s)图3.3.6 电机调速系统方块图K例例3.3.1 某电机调速反馈控制系统如图某电机调速反馈控制系统如图3.3.6所示，其中所示，其中为电机为电机的时间常数，的时间常数，K为放大器的放大倍数，若希望系统的调整时间为放大器的放大倍数，若希望系统的调整时间ts=0.1s，参数，参数和和K该如何选择？该如何选择？解解 系统的闭环传递函数为：系统的闭环传递函数为： 依题意，有3T=0.1s，即故参数和K应满足1+K=30。11s 凡是由二阶微分方程描述的系统，称为二阶凡是由二阶微分方程

42、描述的系统，称为二阶系统。在控制工程中的许多系统都是二阶系统，系统。在控制工程中的许多系统都是二阶系统，如电学系统、力学系统等。即使是高阶系统，如电学系统、力学系统等。即使是高阶系统，在简化系统分析的情况下有许多也可以近似成在简化系统分析的情况下有许多也可以近似成二阶系统。因此，二阶系统的性能分析在自动二阶系统。因此，二阶系统的性能分析在自动控制系统分析中有非常重要的地位。控制系统分析中有非常重要的地位。 3.4 3.4 二阶系统时域分析二阶系统时域分析 2nn22nios2ssXsX sXi sXo sE- n2n2ss sXi sXo2nn22ns2s 振荡角频率振荡角频率无阻尼自然无阻尼

43、自然阻尼比阻尼比 n - 1Ts2sT122 二阶系统的数学模型二阶系统的数学模型二阶系统特征方程：0222nnsss01 1 122 . 1nns0 1 22 . 1ns0 1 10 322 . 1nnjs0 0 42 . 1njs122 . 1nns特征方程的根： n 2n1j n21tg0s2n1j t1tsin11d2ten dnnnjjs 1 10 1.22 . 1欠阻尼 s1s2ssX2nn22no 此时：此时：2nn2s2scbssa t1tsin1tcos1txa,b,cdt2dtoeenn 求出：求出： 3.4.2 典型二阶系统的单位阶跃响应典型二阶系统的单位阶跃响应x0(t

44、)wnttpP54 图3-10 二阶 振 荡环 节 单位阶 跃 响 应曲线2 . 04 . 06 . 08 . 0 t1tsin11txd2toen 衰减振荡00 n2nn2 . 1j1js0 2.无阻尼 s1ssX2n22no 此时：此时：2n2sss1 t1tcos1txno xo(t)P54 图3-13 零阻尼二阶 系统 单位阶 跃 响 应曲线等幅振荡01 nnnjs 1 1 3.22 . 1临界阻尼 s1ssX2n2no 此时：此时： n12n2sbsbsa t1t1tx,ba,beettno12nn 求出：求出： txo(t)P54 图3-11 临 界阻尼二阶 系统 单位阶 跃 响

45、应曲线不振荡01 1 1 4.22 . 1nns过阻尼 s1sssssX212no 此时：此时： t1cbatxa,b,ceetstso21 求出：求出： 21sscssbsa xo(t)P54 图3-12 过 阻尼二阶 系统 单位阶 跃 响 应曲 线不振荡动态过程更长 0 5.1s2nn2 . 1 s01负阻尼 1s1sssssX1212no 不相等正实根xo(t)0tP55 图3-15 负 阻尼 二阶 系统 的 单调发 散响 应单调发散 21sscssbsa t1cbatxa,b,ceetstso21 求出：求出：xo(t)0tP55 图3-14 负 阻尼 二阶 系统 的 发 散振 荡响

46、应 1- 02 共轭复根001 0 5.1s2nn2 . 1 负阻尼发散振荡 2nn22nos2ssX 此时：此时： 1sXttxii dn2nn2 . 1j1js 10 1. 22n2n2n2n1s11 t1sin1tx2nt2noen 3.4.2 3.4.2 二阶系统的单位脉冲响应二阶系统的单位脉冲响应024681012-1-0.8-0.6-0.4-0.200.20.40.60.81xo(t)ntnP61 图3-22 欠阻尼二阶 系统 的阶 跃 响 应曲线1 . 03 . 05 . 07 . 00 . 1衰减振荡 t1sin1tx2nt2noen 2n2nossX 此时：此时：n2nn2

47、. 11js 1 2. t1ttx,bbet2no12n 求出：求出： 020-0.300.30.6xontnP61 图3-23 临 界阻尼 和 过 阻尼 二阶 系统 单位脉 冲 响 应曲 线111 t1ttx,bbet2no12n 求出：求出： 212nosssssX 此时：此时： 1 3.1s2nn2 . 1 21ssbssa t1batxa,beetstso21 求出：求出： 020-0.300.30.6xontnP61 图3-23 临 界阻尼 和 过 阻尼 二阶 系统 单位脉 冲 响 应曲 线111 t1batxa,beetstso21 求出：求出： t1sin112ttx502nt2

48、nnoen 查拉氏变换表查拉氏变换表3.4.3 二阶系统的单位斜坡响应二阶系统的单位斜坡响应 2iis1sXttx dn2nn2 . 1j1js 10 1. 22nn22nos1s2ssX 此时：此时： 22n2n22n1ss1 2n2n1arctg21arctg2 其中：其中： noittxtx2)()(lim)e(t 时，当P63 图3-24 欠阻尼二阶 系统 单位斜坡 响 应曲 线00.511.522.533.544.5500.511.522.533.544.55n2xo(t)xi(t) 2iis1sXttx nnnjs 1 1 2.22 . 1 2221)( sssXnno此时：nnn

49、nssss212122 )( 1)22( ttttxeetntnonnnoittxtx2)()(lim)e(t时，当P63 图3-25 临 界阻尼二阶 系统 单位斜坡 响 应曲线xi(t)xo(t)n2t0P63 图3-26 过 阻尼二阶 系统 单位斜 坡 响 应曲 线xi(t)xo(t)0tn2例题：例题：s000000j1234561、根据特征根在、根据特征根在S平面的分平面的分布，画出单位阶跃响应，并布，画出单位阶跃响应，并标出对应的序列号；标出对应的序列号；2、指出各响应属于哪种形、指出各响应属于哪种形式：（式：（单调衰减单调衰减 /衰减振荡衰减振荡 等幅振荡等幅振荡 /发散振荡发散振

50、荡 / 单调发散单调发散）s000000j123456xo(t)P54 图3-12 过 阻尼二阶 系统 单位阶 跃 响 应曲线1txo(t)P54 图3-11 临 界阻尼二阶 系统 单位阶 跃 响 应曲线2x0(t)wnttpP54 图3-10 二阶振荡 环 节 单位 阶跃 响 应曲线3xo(t)P54 图3-13 零阻尼二阶 系统 单位阶 跃 响 应曲 线4xo(t)0tP55 图3-14 负 阻尼 二阶 系统 的 发 散振 荡响 应5xo(t)0tP55 图3-15 负 阻尼 二阶 系统 的 单调发 散响 应61，过阻尼，过阻尼=1，临界阻尼，临界阻尼01，欠阻尼，欠阻尼=0，无阻尼，无阻

51、尼-10，负阻尼，负阻尼-1，负阻尼，负阻尼 应和单位脉冲响应。试求该系统单位阶跃响环传递函数为例设单位反馈系统的开2s1s2sG sXi sXo212ss- 222io1s1s2s1s21s1s2sXsX t1ete1tx1s11s1s1s11s1s2sXt1tx1tto22oi 则：则：、 t1tee2dtt1ete1dtxdtt1dttx2ttttoi 则：则：、 习题：3-11、3-12响应曲线从0上升到稳态值的100%所用时间rt响应曲线达到第一个峰值所用时间pt在响应曲线的稳态值上，用稳态值的绝对百分数做一个允许误差范围，响应曲线达到并且永远保持在这一允许误差范围内所用的最小时间s

52、t10ttxopM %100oopoxxtx这些点已被确定0.05或0.023.4.4 二阶系统时域性能指标二阶系统时域性能指标 n 2n1j n21tg0s2n1j t1tsin11d2ten dnnnjjs 1 10 22 . 1 s1s2ssX2nn22no 此时：此时：2nn2s2scbssa t1tsin1tcos1txa,b,cdt2dtoeenn 求出：求出： 欠阻尼二阶系统的动态性能指标欠阻尼二阶系统的动态性能指标 （1）上升时间）上升时间tr 当t=tr时，X o(tr)=1211sin()1n rtd ret sin()0d rt(12 3.)d rtKK ， ，上升时间上

53、升时间tr是是c(t)第一次达到稳态时间第一次达到稳态时间21rdnt 1sin11(t) x2ottdten（2）峰值时间）峰值时间tP tP处有极值，故该处导数值为处有极值，故该处导数值为022sin()cos()011nnttnd Pdd Peett峰值对应振荡第一个周期内极大值21Pdnt 0dttdxo 令令 1sin11(t) x2ottdten st4 调整时间调整时间 2to1txe n-1 的包络线为的包络线为%512tes n-令令05. 0ln1n 2ns105. 0ln1t 得得 n-%212tes 若令若令 t1tsin11txd2toen ns4t ns3t t1t

54、sin11txpd2tpoepn -1-2sinsin pM3 最大超调量最大超调量 sin1121e2 1 -e21potx %100 xxtxoopo dpt 代入代入 100% 100%- e21oopopxxtxM 标准二阶系统瞬态响应指标drt dpt 100% - e21pM %24t%53tnsns l从平稳性看，从平稳性看，越大越好，越大越好， ， %l通常为了获得良好的平稳性和快速性，阻尼比取在通常为了获得良好的平稳性和快速性，阻尼比取在0.40.8之间，之间，相应的超调量相应的超调量25%2.5%。l最佳阻尼比最佳阻尼比0.707。fsttN 2122ndftl振荡次数振荡

55、次数 & 振荡周期：振荡周期：x0(t)wnttpP54 图3-10 二阶 振 荡环 节 单位阶 跃 响 应曲线2 . 04 . 06 . 08 . 0常数）常数）(1n 0246810121400.20.40.60.811.21.41.61.8wn=0.5 wn=1 wn=1.5 wn=2 阻 尼 比 =0. 2常数）常数）(2 . 0 nd SBS 2nn22nios2ssXsX 物理参数性能指标srhhppttKKKK12 . 0Mt和和系统的系统的值下，值下，和和并确定在此并确定在此值值和和确定确定欲使欲使 0.456 0.2 - 解之，得解之，得依题意，依题意，e21pM d

56、dp1t 则则依依题题意意，53. 3456. 01122dn 则则 Ks1KKsK1sssK1K11ssKsXsXh2hio 比较比较与标准二阶系统与标准二阶系统2222nnnss 178. 0K12K21KK5 .1253. 3Knhnh22n 48. 24t65. 01arctg1tns2ddr tFtkxtx ftxMtxMtx ftkxtF iooooooi 即：P60 图3-20 质 量-弹簧-阻尼系统MFi(t)xo(t)kfMfK0.0029pt8.9N求M、k、f 的数值2nnMk,2Mf 有有关关系系： 2nn22n22ios2sk1MksMfsMkk1kfsMs1sFsX

57、 求k 的数值 s9 . 8kfsMs1sFkfsMs1sX2i2o m03. 0k9 . 8s9 . 8kfsMs1slimssXlimx20so0so 由终值定理得由终值定理得 mN29703. 09 . 8k 0.6 0.030.0029 - 解之，得解之，得e21pM96. 16 . 01221t2n2ndp smN8 .1813 .7796. 16 . 02M2fkg3 .7796. 1297kMn22n 2nnMk,2Mf 有有关关系系：误差带进入例系统如图，试求%5t,t ,M , ,sppn 1s2s255002. 04s50s10014s50s100ss2ioXX 2 . 0

58、2T22 . 0515T25Tn2 sXi sXo450100ss02. 0-1Ts2sT122 s753ttMsp1pe2 nd-s16.03 52.7% 100% 习题：3-17、3-18 对于一般二阶以上的单输入单输出线性定常系统，其传递函数可以表示为： nmasasasbsbsbsksXsXn1n1n1nm1m1m1mio nr2qs2spsbsbsbskq1jr1k2kkk2jm1m1m1m 3.5 3.5 高阶系统的瞬态响应 s1sXt1txii 设：设： sXsXsXsXiioo 则：则： q1jr1k2kkk2jm1m1m1ms2spssbsbsbsk rkkkkkkkkkqj

59、jjosspsssX12222111则可以展开成：如果其极点互不相同， 12121 1sin 1coskktkrkktkqjtpjoteteetxkkkkj经拉氏反变换，得 可见，高阶系统的瞬态响应是由一些一阶惯性环节和二阶振荡环节的响应函数迭加组成的。当所有极点均具有负实部时，除了，其它各项随着t而衰减为零，即系统是稳定的。1、系统极点的负实部愈是远离虚轴，则该极点对应的项在瞬态响应中衰减得愈快。反之，距虚轴最近的闭环极点对应着瞬态响应中衰减最慢的项，该极点对（或极点）对瞬态响应起主导作用，称之为主导极点。 工程上当极点A距虚轴的距离大于5倍的极点B距虚轴的距离时，分析时可忽略极点A。2 2

60、、零点与极点之间的距离很近时，此极点对动态过程的影响可以零点与极点之间的距离很近时，此极点对动态过程的影响可以忽略。忽略。 工程上认为某极点与零点之间的距离小于他们本身到原点工程上认为某极点与零点之间的距离小于他们本身到原点距离的距离的1/10时，则极点和零点构成了偶极子，时，则极点和零点构成了偶极子，在传递函数中可在传递函数中可以把偶极子对应项消去，从而可以降低系统的阶次，称为偶极以把偶极子对应项消去，从而可以降低系统的阶次，称为偶极子相消。子相消。 高阶系统通过合理的简化，可以用低阶系统近似例例3.5.1 某高阶系统的传递函数为)6)(52(30)()(2ssssXsXio试分析其动态性能指标Mp