第12章变化的电磁场

1、第十二章变化的电磁场第十二章变化的电磁场研究对象研究对象：研究变化的电场与磁场相互产生的规律：研究变化的电场与磁场相互产生的规律电磁感应电磁感应动生电动势动生电动势感生电动势感生电动势变化的磁场产生电场变化的磁场产生电场变化的电场产生磁场变化的电场产生磁场内容结构内容结构基本应用基本应用自感与互感自感与互感磁场的能量磁场的能量位移位移电流电流假说假说变化的电磁场变化的电磁场安培定理用于交变电安培定理用于交变电流的矛盾流的矛盾涡旋涡旋电场电场假说假说法拉第电磁感应定律、楞次定律法拉第电磁感应定律、楞次定律变化的电磁场变化的电磁场12-1 电磁感应定律电磁感应定律（本次课）（本次课）12-2 动生

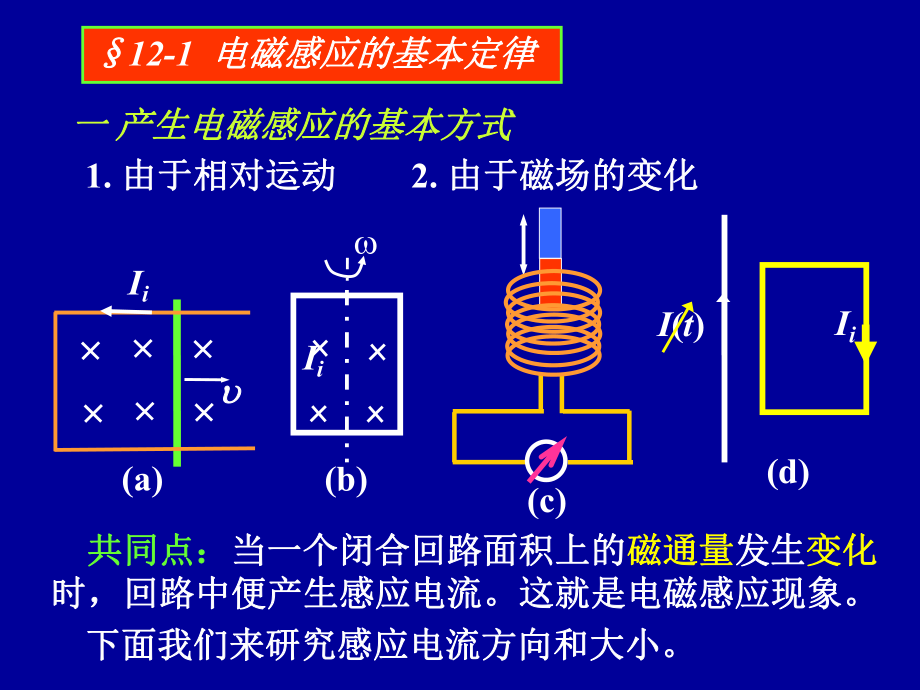
2、电动势动生电动势12-3 感生电动势感生电动势12-1 电磁感应的基本定律电磁感应的基本定律 一一 产生电磁感应的基本方式产生电磁感应的基本方式 Ii 共同点：共同点：当一个闭合回路面积上的当一个闭合回路面积上的磁通量磁通量发生发生变化变化时，回路中便产生感应电流。这就是电磁感应现象。时，回路中便产生感应电流。这就是电磁感应现象。下面我们来研究感应电流方向和大小。下面我们来研究感应电流方向和大小。(a)(b)(c)I(t)Ii(d)1. 由于相对运动由于相对运动2. 由于磁场的变化由于磁场的变化Ii二二.楞次定律楞次定律 闭合导体回路中感应电流的方向闭合导体回路中感应电流的方向,总是总是企图企

3、图使它自使它自身产生的通过回路面积的磁通量身产生的通过回路面积的磁通量,去去阻碍阻碍原磁通量的原磁通量的改变。这一结论叫做改变。这一结论叫做楞次定律楞次定律。 1) 阻碍阻碍的意思是：的意思是：BBIi 感应电流感应电流Ii与与原磁场原磁场B的的反反方向成右手螺方向成右手螺旋关系。旋关系。 若若 m增加增加,感应电流的磁感应电流的磁力线与力线与B反向反向; 若若 m减少减少,感应电流的感应电流的磁力线与磁力线与B同向同向; 感应电感应电流流Ii与原磁场与原磁场B的的正正方向方向成右手螺旋关系。成右手螺旋关系。Ii2)企图企图 感应电流总是感应电流总是企图企图用它产生的磁通用它产生的磁通,去去阻

4、碍阻碍原磁通原磁通的改变，但又无法阻止原磁通的变化，因而感应电流的改变，但又无法阻止原磁通的变化，因而感应电流还是不断地产生。还是不断地产生。3)楞次定律是能量守恒定律的必然结果。楞次定律是能量守恒定律的必然结果。 要想维持回要想维持回路中电流，必须有外力不断作路中电流，必须有外力不断作功。这符合能量守恒定律。功。这符合能量守恒定律。 则不需则不需外力作功，导线便会自动运动下去，从而不断获得电外力作功，导线便会自动运动下去，从而不断获得电能。这显然违背能量守恒定律能。这显然违背能量守恒定律。按楞次定律，按楞次定律，如果把楞次定律中的如果把楞次定律中的“阻碍阻碍”改为改为“助长助长”，fmfm4

5、)对闭合导体回路而言对闭合导体回路而言, 感应电动势的方向感应电动势的方向和和感应感应电流的方向是相同的。电流的方向是相同的。 i 因而回路中感应电动势的方向因而回路中感应电动势的方向,也用楞次定律来也用楞次定律来判断。判断。 I三三 .法拉第电磁感应定律法拉第电磁感应定律 法拉第从实验中总结出法拉第从实验中总结出回路中的感应电动势回路中的感应电动势为为dtdmi 1. m 是通过回路面积的磁通量；是通过回路面积的磁通量； smBdscos对匀强磁场中的平面线圈：对匀强磁场中的平面线圈：cosBSm2.用法拉第电磁感应定律解题的步骤如下：用法拉第电磁感应定律解题的步骤如下：(i)首先求出回路面

6、积上的磁通量：首先求出回路面积上的磁通量：(对平面正法向无法确定则取正值对平面正法向无法确定则取正值)感应电动势的大小由磁通量变化的感应电动势的大小由磁通量变化的快慢快慢决定！决定！ “-”的意义：的意义：负号负号是是楞次定律楞次定律的数学表示。的数学表示。用用楞次定律楞次定律或如下或如下符号法则符号法则判定感应电动势的方向判定感应电动势的方向: 若若 i 0, 则则 i 的方向与原磁场的的方向与原磁场的正正方向组成右手螺方向组成右手螺旋关系；旋关系； 若若 i 0, i 的方向与原磁场的的方向与原磁场的正正方向组成右手螺方向组成右手螺旋关系旋关系,即顺时针方向。即顺时针方向。 由由楞次定律可

7、知，此时圆线楞次定律可知，此时圆线圈内感应电动势的方向应是顺时针的。圈内感应电动势的方向应是顺时针的。 因因t=0.01s时时,函数函数sin100 t是减是减小的小的,所以所以通过线圈面积上的磁通量通过线圈面积上的磁通量 m也也是减小的。是减小的。 i 例题例题12-2 一长直螺线管横截面的半径为一长直螺线管横截面的半径为a, 单位单位长度上密绕了长度上密绕了n匝线圈，通以电流匝线圈，通以电流I=Iocos t(Io、 为为常量常量)。一半径为。一半径为b、电阻为电阻为R的单匝圆形线圈套在螺的单匝圆形线圈套在螺线管上，如图所示。求圆线圈中的感应电动势和感应线管上，如图所示。求圆线圈中的感应电

8、动势和感应电流电流。 解解 由由 m=BScos 得得 m=onI b2 a2dtdNmitIanoosin2tIanRRIooiisin12BIab如果如果b0, 则则 i 的方向与的方向与dl 同向；同向；若若 i 0, 所以所以 i 的方向与的方向与l 同向同向,即由即由a到到b。 (1)三垂直三垂直( B 直导线直导线l )。lBi)( abB-+首先规定首先规定l 的方向由的方向由a到到b,如图所示。如图所示。lab=l (2)任意形状的导线在任意形状的导线在匀强匀强磁场中磁场中平移平移时，时， abBdll 在在匀强匀强磁场中磁场中,弯曲导线平移弯曲导线平移时所产生的动生时所产生的

9、动生电动势等于电动势等于从起点到终点的从起点到终点的直导线直导线所产生的动生所产生的动生电动势电动势 。lB )()(BbadldlbaiB)(ab=lab=bc=l, 求求 Va-Vc= ? d abc= adc= ad = Bl(1-cos ) 电动势的方向由电动势的方向由c指向指向a; a点比点比c点电势高。点电势高。所以所以 Va-Vc= Bl(1-cos ) 导线在匀强磁场中运动，导线在匀强磁场中运动， B。lBi)( ab= Bab bc= Bl ,cbcos ,bacVa-Vc= Bl(1-cos ) abcl abcl Bl求求 Va-Vb= ?Va-Vb=ab=ab =BR

10、2 4545RbaoBR 2 abVa-Vc= + Blsin d abc= dc abcVa-Vc= ?= Blsin 例题例题12-11 均匀磁场被限制在两平面之间，边长均匀磁场被限制在两平面之间，边长l的正方形线圈匀速的正方形线圈匀速 通过该磁通过该磁场。哪个场。哪个I-t图形是正确图形是正确的？的？(设逆时针为电流的正方向，不计线圈的自感设逆时针为电流的正方向，不计线圈的自感)当线圈各边都在磁场中时，当线圈各边都在磁场中时，Va-Vb=问题：问题：ab+Bl Ito(A)Ito(C)Ito(B)Ito(D) 解解:l0 xBdx=221lB 负号说明：负号说明： i的方向由的方向由p指

11、向指向o，o点电势高点电势高。2polB21VV请记住这个转动公式请记住这个转动公式:221lBi 例题例题12-9 一条金属细直棒一条金属细直棒op(长为长为l)绕绕o点以角速点以角速度度 在垂直于匀强磁场在垂直于匀强磁场B的平面内匀速转动的平面内匀速转动,求求Vo-Vp=?导线dlBBBdli,cos(),sin()opBxdxAo=l1, oC=l2VA-VC=ACo)ll (B222121 若若l1l2, 则则A点电势高；点电势高；若若l1l2, 则则C点电势高点电势高。三角形绕轴三角形绕轴ab转动转动, bc=l 。Vb-Vc=三角形回路三角形回路: i= 2lB21221lBiBA

12、C ocbaB0上讲上讲感应电动势感应电动势变化m法拉第电磁感应定律法拉第电磁感应定律计算计算dtdNmi（或用楞次定律判断方向）（或用楞次定律判断方向）感生电动势感生电动势动生电动势动生电动势lBi)(l dBi 导导体体)( No.11-2abB i =Bl RBlRIiicosIi 例题例题12-11 有一很长的长方的有一很长的长方的U形导轨形导轨,与水平面与水平面成成 角角,裸导线裸导线ab可在导轨上无摩擦地下滑可在导轨上无摩擦地下滑,导轨位于磁导轨位于磁感应强度为感应强度为B的的垂直向上的均匀磁场中垂直向上的均匀磁场中,如图所示。设如图所示。设导线导线ab的质量为的质量为m,长度为长

13、度为l,导轨上串接有一电阻导轨上串接有一电阻R，导导轨和导线轨和导线ab的电阻略去不计的电阻略去不计,abcd形成电路形成电路, t=0, =0; 试试求求: 导线导线ab下滑的速度下滑的速度 与时间与时间t的函数关系。的函数关系。 解解 导线导线ab在安培力和重力在安培力和重力作用下，沿导轨斜面运动。作用下，沿导轨斜面运动。cos RabcdB知知:lBi)(由由Fm=IilB,cos22RlB 沿斜面方向应用牛顿第沿斜面方向应用牛顿第二定律：二定律：dtdmRlBmg222cossinsin)cos(2gmRBld- dtRBlIicosIiRabcdB BmgFmmaFmgmcossin

14、tmRBleCgmRBl2)cos(22sin)cos( 122)sin)cos(ln()cos(CtgmRBlBlmRsin)cos(2gmRBld- dt由由 t=0, =0, 得得C2=-gsin )1()cos(sin2)cos(2tmRBleBlmgR 导体不动导体不动, 磁场磁场随时间随时间变化变化,导体中便产生感应电导体中便产生感应电动势动势感生电动势感生电动势。 12-3 感生电动势感生电动势 涡旋电场涡旋电场1.现象现象2.原因原因 当螺线管中电流发生变化，引起螺线管中的磁场当螺线管中电流发生变化，引起螺线管中的磁场变化时，套在外边的圆环中便产生电动势。变化时，套在外边的圆环

15、中便产生电动势。 是什么力驱使导线中是什么力驱使导线中的电荷运动，从而产生电的电荷运动，从而产生电动势呢？动势呢？ 不是洛仑兹力。不是洛仑兹力。 也不是静电力。也不是静电力。BIab 麦克斯韦的这个假设已为实践所证实，是麦克斯麦克斯韦的这个假设已为实践所证实，是麦克斯韦电磁理论的基本原理之一。韦电磁理论的基本原理之一。 麦克斯韦认为：麦克斯韦认为：变化的磁场变化的磁场要在其周围的空间要在其周围的空间激激发发一种电场一种电场,叫做叫做感生电场感生电场(涡旋电场涡旋电场)Ei。 圆环导线中的感生电动势正是圆环导线中的感生电动势正是感生电场感生电场对自由电对自由电子作用的结果。子作用的结果。 BIa

16、b3. 性质性质 1)感生电场的环路定理感生电场的环路定理Ll dE感由电动势定义：由电动势定义： ldELK感由法拉第定律：由法拉第定律：t ddm感SSdtB SLSdtBl dE感得：得：SLSdtBl dE感表明：只要存在着表明：只要存在着变化的磁场变化的磁场，就一定会有，就一定会有感生电场感生电场。感生电场的环流并不等于零，故感生电场感生电场的环流并不等于零，故感生电场是非保守场是非保守场。 2)感生电场的高斯定理感生电场的高斯定理 因感生电场是非保守场，则可认为其电力线因感生电场是非保守场，则可认为其电力线是闭合曲线，故其穿过任一封闭曲面的通量应恒等是闭合曲线，故其穿过任一封闭曲面

17、的通量应恒等于零。于零。0d SEs感感生电场感生电场是无源场是无源场两种电场比较两种电场比较静止电荷静止电荷变化磁场变化磁场内静qSEs01d0dLlE静有源，保守场有源，保守场0d sSE感lELd感StBSd无源，非保守场无源，非保守场(涡旋涡旋)不能脱离源电荷存在不能脱离源电荷存在可以脱离可以脱离“源源”在空间传播在空间传播静Eq静F感Eq感F起源起源性质性质与源的与源的联系联系对场中电对场中电荷的作用荷的作用静电场静电场感生电场感生电场4. 感生电场存在的实验证明感生电场存在的实验证明 1) 涡电流涡电流 2)电子感应加速器电子感应加速器5.计算公式计算公式dtdm 感生电场的方向可

18、用感生电场的方向可用楞次定律楞次定律来确定。来确定。按电动势的定义：按电动势的定义：感ldlE 感 感生电场感生电场E感感的电力线是的电力线是围绕磁力线围绕磁力线的的闭合曲线闭合曲线；0ddtBB感E感EB感E感E0ddtB 例题例题12-12 一半径为一半径为R的圆柱形空间区域内存在的圆柱形空间区域内存在着由无限长通电螺线管产生的均匀磁场着由无限长通电螺线管产生的均匀磁场,磁场方向垂磁场方向垂直纸面向里，如图所示。当磁感应强度以直纸面向里，如图所示。当磁感应强度以dB/dt的变的变化率均匀减小时化率均匀减小时,求圆柱形空间区域内、外各点的感求圆柱形空间区域内、外各点的感生电场。生电场。 由楞

19、由楞次定律判定，感生电场的方向是次定律判定，感生电场的方向是顺时针的，顺时针的，Rr=Ei 2 rrR:dtdBrEi2 Ei 2 rdtRBd)(2 dtdBrREi22 Ei 2 rdtrBd)(2 rR: 你能完成这个积分吗？不你能完成这个积分吗？不妨试试。妨试试。BAidlEi iERABodlEiBAcos riEdl 连接连接oA、oB组成回路。组成回路。241RBm dtdm感dtdBR 42 由楞次定律知，回路电动势方向为逆时针，因此由楞次定律知，回路电动势方向为逆时针，因此导线导线AB中的感生电动势由中的感生电动势由A指向指向B。B点电势高。点电势高。 由于由于oA和和oB不

20、产生电动势不产生电动势,故回路电动势就是导线故回路电动势就是导线AB中的中的电动势。电动势。cosdlEAoi感=0感ERABoo.ABAB(填填、或或=)dtBsdi)(连接连接oA、oB组成回路组成回路,由由得知。得知。AB (2)如图所示的长直导线如图所示的长直导线中的感生电动势中的感生电动势:dtdBRi 22 dtdBso.R问题问题: 圆柱形空间区域内存在圆柱形空间区域内存在着均匀磁场，着均匀磁场， (1)对直导线对直导线AB和弯曲的导线和弯曲的导线AB：感应电动势感应电动势动生电动势动生电动势 感生电动势感生电动势自感电动势自感电动势互感电动势互感电动势 本本 节节12-4 自感

21、和互感自感和互感 I I变变（B B变）变）一一.自感现象自感现象 自感系数自感系数 1 1. .现象：现象：由于回路电流变化，引起由于回路电流变化，引起自已自已回路的回路的磁通量变化磁通量变化，而在回路中激起感应电动势的现象叫做而在回路中激起感应电动势的现象叫做自感现象自感现象。相应的电动。相应的电动势叫做势叫做自感电动势自感电动势。 (1) 定义定义 设回路有设回路有N匝线圈，通过线圈面积上的磁通量为匝线圈，通过线圈面积上的磁通量为 m,则通过线圈的磁通链数则通过线圈的磁通链数: 式中比例系数式中比例系数L,叫做线圈的叫做线圈的自感自感系数系数,简称自感。简称自感。 对对非非铁磁质铁磁质,

22、 L是常量是常量,大小大小与线圈的形状大小及磁介质有关。与线圈的形状大小及磁介质有关。对铁磁质对铁磁质, L不再是常量不再是常量(与电流有关与电流有关)。BIN m IN m =LI2.2.自感系数自感系数 当当I增加时，自感电动势原电流方向相反增加时，自感电动势原电流方向相反 当当I减小时，自感电动势与原电流方向相同减小时，自感电动势与原电流方向相同 A）在）在L一定的情况下，自感电动势与电流的变化率成正比。一定的情况下，自感电动势与电流的变化率成正比。 B）对于相同的电流变化率，）对于相同的电流变化率，L越大的线圈，产生的自感电动越大的线圈，产生的自感电动势越大。势越大。 从大小上看：从大

23、小上看： 自感电动势为自感电动势为()mLd Ndt 如果线圈自感系数如果线圈自感系数L为常量为常量,则则dtdILL (2) 物理意义物理意义 可见，可见，L越大的线圈，回路中的电流就越不容易改变。越大的线圈，回路中的电流就越不容易改变。N m =LI 从方向上看：从方向上看： 可见，自感电动势的作用是反抗回路中的电流变化。可见，自感电动势的作用是反抗回路中的电流变化。 ()d LIdt 可见回路中的自感具有使回路保持原有电流可见回路中的自感具有使回路保持原有电流不变的性质，这一性质与力学中物体的惯性相似，不变的性质，这一性质与力学中物体的惯性相似，因此，因此，自感系数自感系数L被视为电磁惯

24、性大小的量度，被视为电磁惯性大小的量度，反映了自感电动势阻碍电流变化的能力反映了自感电动势阻碍电流变化的能力。由上可得计算自感系数的方法：由上可得计算自感系数的方法：INLm dtdILL INLm（少用）（少用）I设设smSdBNN求求分布分布B（多用）（多用）(3) (3) 计算计算L的单位的单位（SI制）制） ：亨利（亨利（ H） 例题例题12-14 一单层密绕、长为一单层密绕、长为l、截面积为、截面积为S的长的长直螺线管直螺线管,单位长度上的匝数为单位长度上的匝数为n, 管内充满磁导率为管内充满磁导率为 的均匀磁介质。求该长直螺线管的自感系数。的均匀磁介质。求该长直螺线管的自感系数。

25、解解 设在长直螺线管中设在长直螺线管中通以电流通以电流I，则，则B= n I m =BS= nISINLm ,Sln2 Sl=VVnL2 最后得最后得 提高提高L的途径的途径增大增大V提高提高n放入放入 值高的介质值高的介质 （实用）（实用）=N nS解解rNIB 2 smBds cosdrr m 12ln2RRNIh 122ln2RRhNINLm 21RRrNI 2hdr 例题例题12-15 一矩形截面螺线环，共一矩形截面螺线环，共N匝，匝，求它的自感求它的自感。 例题例题12-16 求同轴电缆单位长度上的自感。求同轴电缆单位长度上的自感。解解rIB 2(arb) smBds cos m a

26、bIln2 abILmln2 badrrI 2abIIdrr二二 .互感互感 1. 1. 现象：现象：由于一个线圈中电流发生变化而在附由于一个线圈中电流发生变化而在附近的另外一个线圈中产生感应电动势的现象叫做近的另外一个线圈中产生感应电动势的现象叫做互感互感现象。这种感应电动势叫做现象。这种感应电动势叫做互感电动势互感电动势。N2 21=M1I1N1 12=M2I2 实验证明，实验证明，M1=M2=M。比例系数比例系数M,叫做两线圈的叫做两线圈的互感系数互感系数, 简称互感。简称互感。I112B2.2.互感系数互感系数,INM1212 M M在数值上等于任一线圈中单在数值上等于任一线圈中单位电

27、流的磁场，穿过另一线圈位电流的磁场，穿过另一线圈的磁通链。的磁通链。 互感系数互感系数M决定于两线圈的形状、大小、匝数、决定于两线圈的形状、大小、匝数、相对位置相对位置及周围的磁介质。在非铁磁介质的情况下及周围的磁介质。在非铁磁介质的情况下, M与电流无关，在铁磁质中与电流无关，在铁磁质中, M将受线圈中电流的影将受线圈中电流的影响。响。,INM1212 问题：问题：两线圈怎样放置，两线圈怎样放置，M =0？M =0(2) 互感电动势互感电动势t dIdMt ddN121221tdIdMtddN212112:M当一个线圈中电流变化率为一个单位时，在当一个线圈中电流变化率为一个单位时，在相邻另一

28、线圈中引起的互感电动势。相邻另一线圈中引起的互感电动势。dtdIM121 dtdIM212 由此看来，在电流变化率相同的条件下，某两个线圈的由此看来，在电流变化率相同的条件下，某两个线圈的互感系数大，这两个线圈的互感电动势也就大。互感系数大，这两个线圈的互感电动势也就大。 可见，互感系数反映了两个线圈的可见，互感系数反映了两个线圈的相互感应的能力相互感应的能力，或，或者说反映了两个线圈在者说反映了两个线圈在磁方面联系的紧密程度磁方面联系的紧密程度。由上可得计算互感系数的方法：由上可得计算互感系数的方法：,INM1212 ,INLm 计算自感系数的方法：计算自感系数的方法：比较！比较！(3) (

29、3) 计算计算得得1212INM设设I1 I1的磁场分布的磁场分布 穿过线圈穿过线圈2的的1B212N2s12212SdBNN 例题例题12-17 一无限长直导线与一矩形线框在同一无限长直导线与一矩形线框在同一平面内，如图所示。当矩形线框中通以电流一平面内，如图所示。当矩形线框中通以电流I2=Iocos t(式中式中Io和和 为常量为常量)时，求时，求长直导线中的感长直导线中的感应电动势。应电动势。解解 假定长直导线中通以电流假定长直导线中通以电流I1, 则则rIBo 21 sBdscos21drr 21cbaIoln21 cbaINMoln21212 bcrIo 21adrcbaI212dt

30、dIM212 tIcbaoo sinln2cbaINMoln21212 注：注： 本题还可令长直导本题还可令长直导线中通以电流线中通以电流I2,直接由法拉第直接由法拉第电磁感应定律求得其在矩形线电磁感应定律求得其在矩形线框中产生的互感电动势，该电框中产生的互感电动势，该电动势与待求电动势大小相等。动势与待求电动势大小相等。cbaI212I2=Iocos t 例题例题12-18 一长直磁棒上绕有自感分别为一长直磁棒上绕有自感分别为L1和和L2的两个线圈，如图所示。在理想耦合的情况下，求它的两个线圈，如图所示。在理想耦合的情况下，求它们之间的互感系数。们之间的互感系数。 解解 设自感设自感L1长长

31、l1、N1匝，匝，L2长长l2、N2匝，并在匝，并在 L1 中通以电流中通以电流I1。考虑到理想耦合的情况，有。考虑到理想耦合的情况，有sIn1121 1212INM 21sNn 211111NsllNNn 12121NNVn ,11InB ,1211VnL 121NNLM 1234SL1L2同理，若在同理，若在 L2 中通以电流中通以电流I2，则有，则有,212NNLM 前已求出：前已求出：121NNLM 得得21LLM 必须指出必须指出,只有在理想耦合只有在理想耦合的情况下的情况下,才有才有 的关的关系系;一般情形时一般情形时, ,而而0k1,k称为耦合系数称为耦合系数,视视两线圈的相对位

32、置而定。两线圈的相对位置而定。 21LLM 21LLkM 1234SL1L2问题：问题： 1.将将2、3端相连接，这个线圈的自感是多少？端相连接，这个线圈的自感是多少？IL1 设线圈中通以电流设线圈中通以电流I，则穿过线圈面积的磁，则穿过线圈面积的磁通链为通链为21LLM IL 2121LL2LLL IL2 MI2 1234SL1L2 当当L1= L2= L0时，时， L=4 L0 顺接顺接MLL221 2.将将2、4端相连接，这端相连接，这个线圈的自感是多少？个线圈的自感是多少？2121LL2LLL 1234SL1L2 当当L1= L2= L0时，时， L=0 自感相同的两线圈反接又称为无感

33、连接。自感相同的两线圈反接又称为无感连接。问题：问题：如何用线绕方法制作纯电阻？如何用线绕方法制作纯电阻？双线并绕。双线并绕。 反接反接12-5 磁场能量磁场能量一一 .自感磁能自感磁能 tItRdtILIdIIdt0002电源发出电源发出 的总功的总功电源反抗电源反抗自感的功自感的功电阻上的电阻上的 焦耳热焦耳热221LIKRLRIdtdILII2 1 .通电线圈中的磁能通电线圈中的磁能dtdIL IR 电源反抗自感作功过程，也是线圈中磁场的建立电源反抗自感作功过程，也是线圈中磁场的建立的过程。可见，电源克服自感电动势所作的功，就的过程。可见，电源克服自感电动势所作的功，就转化为转化为线圈线

34、圈L中的磁能中的磁能:221LIwm 2.磁场能量密度磁场能量密度 设螺线管单位长度上设螺线管单位长度上n匝，体积为匝，体积为V，其中充满磁，其中充满磁导率为导率为的均匀磁介质的均匀磁介质,L= n2V, 221LIwm VHVB 222121B= nI= H 因为长直螺线管内磁场是均匀的因为长直螺线管内磁场是均匀的,所以磁场能量所以磁场能量的分布也是均匀的。于是的分布也是均匀的。于是磁场能量密度磁场能量密度为为222121HBm VHVBwm 222121 上式虽然是从载流长直螺线管为例导出的上式虽然是从载流长直螺线管为例导出的,但可但可以证明该式适用于一切磁场以证明该式适用于一切磁场(铁磁

35、质除外铁磁质除外)。 例题例题12-19 一细螺线环有一细螺线环有N=200匝，匝，I=1.25A, 通过环截面积的磁通量通过环截面积的磁通量 m=510-4wb, 求求螺线环中螺线环中储存的磁能。储存的磁能。解解 =0.125JINLm mNI 21221LIwm 例题例题12-24 同轴电缆由两个同轴薄圆筒构成同轴电缆由两个同轴薄圆筒构成, 流流有等值反向电流有等值反向电流I，两筒间为真空，计算电缆单位长，两筒间为真空，计算电缆单位长度内所储存的磁能。度内所储存的磁能。解解rIBo 2(R1rR2)oB22 mwrdrIRRo 2142122ln4RRIo 也可用也可用 计算。计算。221

36、LIwm 21RRrdr 2R1R2II1rdr第十二章变化的电磁场第十二章变化的电磁场研究对象研究对象：研究变化的电场与磁场相互产生的规律：研究变化的电场与磁场相互产生的规律电磁感应电磁感应动生电动势动生电动势变化的磁场产生电场变化的磁场产生电场内容结构内容结构变化的电磁场变化的电磁场涡旋涡旋电场电场假说假说法拉第电磁感应定律、楞次定律法拉第电磁感应定律、楞次定律感生电动势感生电动势自感自感互感互感磁场磁场能量能量变化的电场产生磁场变化的电场产生磁场?位移位移电流电流假说假说安培定理用于交变电安培定理用于交变电流的矛盾流的矛盾 前面讲到，前面讲到，变化的磁场激发电场变化的磁场激发电场(感生电

37、场感生电场)。那么，那么，会不会有相反的情况：变化的电场也会激发磁场？会不会有相反的情况：变化的电场也会激发磁场？ 麦克斯韦在研究了安培环路定律应用于交流电路中麦克斯韦在研究了安培环路定律应用于交流电路中出现的矛盾以后，提出了出现的矛盾以后，提出了位移电流位移电流的概念，对上述问的概念，对上述问题作出了圆满的回答。题作出了圆满的回答。12-6 位移电流位移电流 在在稳恒电流稳恒电流条件下条件下,安培环路定律为安培环路定律为式中式中: I0内内是穿过以闭合回路是穿过以闭合回路l为边界的为边界的任意曲面任意曲面S的的传导电流传导电流的代数和。的代数和。 lIl dH内内0 一一. 问题的提出问题的

38、提出 对开放电路中的非稳恒电流对开放电路中的非稳恒电流,是否适用？是否适用？ I (平面平面S1)0 (曲面曲面S2) 可见，在非稳恒的条件下可见，在非稳恒的条件下,具有上述形式的安培环路定律具有上述形式的安培环路定律不再适用不再适用,原因是在非稳恒的条原因是在非稳恒的条件下，传导电流不再连续件下，传导电流不再连续，必，必须加以修正。须加以修正。 ldlHkIlES2 麦克斯韦注意到极板处电流的不连续引起极板上麦克斯韦注意到极板处电流的不连续引起极板上电量的变化，而电量的变化又导致板间电场的变化。电量的变化，而电量的变化又导致板间电场的变化。 二二.位移电流的概念位移电流的概念 S1 假设在假

39、设在dt内，通过电路上任意截面的电荷为内，通过电路上任意截面的电荷为dq，则导线中的电流强度为则导线中的电流强度为 可见，电路中的可见，电路中的传导电流强度传导电流强度=电容器电容器极板上极板上电量对时间的变化率电量对时间的变化率。 极板上的极板上的传导电流密度传导电流密度=极板上的电荷面密度的极板上的电荷面密度的时间变化率时间变化率。令极板面积为令极板面积为S 麦克斯韦研究了导体中的传导电流和电场变化麦克斯韦研究了导体中的传导电流和电场变化的关系。的关系。dtdqI 由于电场的变化源于极板上电荷的变化，由于电场的变化源于极板上电荷的变化，故先来探寻传导电流与极板电荷变化的关系故先来探寻传导电

40、流与极板电荷变化的关系.(q为极板上的电量为极板上的电量),SdtdqSI,dtdJ即 两极板间两极板间，有变化的电场有变化的电场：,oE dtddtdD (极板中的传导电流密度极板中的传导电流密度)dtdqI ,dtdJ Eo 电位移电位移D对时间的变化率对时间的变化率kIlES2S1D J JdtDd 由于由于D与与J同方向，故同方向，故SDe Idtde (极板内的传导电流强度极板内的传导电流强度)SJSdtDd JdtDd kIlES2S1ISJ 若把若把 也看作也看作“电流电流”，则无论选择，则无论选择S1或或S2 ，都，都会使会使 的环流取得同一个确定值，而不致产生矛盾。的环流取得

41、同一个确定值，而不致产生矛盾。dtde H位移电流密度：位移电流密度：位移电流强度：位移电流强度：dtdIed 即即:通过电场中某面积的通过电场中某面积的位移电流强度位移电流强度等于通过该面等于通过该面积的积的电位移通量电位移通量对时间对时间的变化率的变化率；电场中某点的；电场中某点的位移位移电流密度电流密度等于该点等于该点电位移矢量电位移矢量对时间对时间的变化率的变化率。 把把电场的变化电场的变化看作看作是一种电是一种电流流，这就是麦克斯韦位移电流的，这就是麦克斯韦位移电流的概念。麦克斯韦指出：概念。麦克斯韦指出：tDJd kIlES2S1全电流全电流=传导电流传导电流+位移电流位移电流全电

42、流总是连续的。全电流总是连续的。 麦克斯韦指出：麦克斯韦指出：位移电流位移电流(电场的变化电场的变化)与传导与传导电流一样，也要在周围的空间激发磁场电流一样，也要在周围的空间激发磁场。 因此因此,在非稳恒情况下在非稳恒情况下,安培环路安培环路定律的一般形式为定律的一般形式为位移位移电流电流 dlIIl dH0三三. 全电流定律全电流定律 安培环路定律的推广安培环路定律的推广 传导传导+运流运流kIlES2S1+运流电流运流电流 就就磁效应磁效应而论，而论，位移电流位移电流与与传导电流传导电流完全完全平等平等。 位移电流：位移电流：仅仅意味着仅仅意味着电场的变化电场的变化；可存在；可存在于任何介

43、质于任何介质(包括真空包括真空)中；中；四四. 位移电流的性质位移电流的性质传导电流：传导电流：电荷的运动电荷的运动；只存在于导体中；只存在于导体中；有焦耳热。有焦耳热。无焦耳热。无焦耳热。 位移电流的实质在于揭示出变化的电场要激位移电流的实质在于揭示出变化的电场要激发磁场这一事实。发磁场这一事实。 例题例题12-23 平行板电容器的电容平行板电容器的电容C=20 F，两板，两板上电压变化率为上电压变化率为dU/dt=1.50 105V.s-1，求两板间的位，求两板间的位移电流强度。移电流强度。解解 CUq dtdUC =3A IdtdqA3IId 例题例题12-24 如图所示如图所示, 一电

44、量为一电量为q的点电荷的点电荷, 以匀以匀角速度角速度 作半径作半径R的圆周运动。设的圆周运动。设t=0时，时，q所在点的所在点的坐标为坐标为(R,0),求圆心求圆心o处的位移电流密度。处的位移电流密度。解解 ,tDJd 24 RqEDo 0 tDJd,42RqEo tDJd tDJd )sincos(42tjtiRq )(42reRqD )cossin(42tjtiRq xyR oq tre位移电流密度：位移电流密度：即即:通过电场中某面积的通过电场中某面积的位移电流强度位移电流强度等于通过该面等于通过该面积的积的电位移通量电位移通量对时间对时间的变化率的变化率；电场中某点的；电场中某点的位

45、移位移电流密度电流密度等于该点等于该点电位移矢量电位移矢量对时间对时间的变化率的变化率。 tDJd kIlES2S1上讲上讲:位移电流强度：位移电流强度：dtdIed 例题例题12-25 一圆形极板的平行板电容器一圆形极板的平行板电容器,极板半径极板半径R=0.1m, 板间为真空。给电容器充电的过程中板间为真空。给电容器充电的过程中,板间电板间电场对时间的变化率场对时间的变化率dE/dt=1.01013V/m.s, 求求:(1)两板间两板间的位移电流强度；的位移电流强度；(2)离中心离中心r(rR)处的磁感应强度。处的磁感应强度。解解 (1)位移电流密度的大小为位移电流密度的大小为dtdEdt

46、dDJod R两板间的位移电流强度：两板间的位移电流强度：dtdERRJIodd22 =2.78A 由于由于E ，所以，所以位移电位移电流密度流密度 与与E的方向相同，的方向相同，即从正极流向负极。即从正极流向负极。dtEdJod B.2 r =oJd. r2dtdEdtdDJod rdtdEBoo 2r 510181 (2)由安培环路定律得由安培环路定律得RrB loIl dB内内电流呈柱形分布，磁场方向如图中的电流呈柱形分布，磁场方向如图中的圆周切线。圆周切线。 例题例题12-26 一圆形极板的真空平行板电容器，板间一圆形极板的真空平行板电容器，板间距离为距离为d，两极板之间有一长宽分别为

47、，两极板之间有一长宽分别为a和和b的矩形线的矩形线框框,矩形线框的一边与圆极板的中心轴线重合，如图矩形线框的一边与圆极板的中心轴线重合，如图所示。两极板上加上电压所示。两极板上加上电压U12=Uocos t，求，求矩形线框矩形线框的电压的电压U=?解解 板间电场：板间电场：tdUdUEo cos12dtdEdtdDJod tdUoo sin位移电流密度：位移电流密度：dU=?abB.2 r=oJd. r2rJBdo2 trdUooo sin2 smcosBds tdabUooo sin42dtdmi tdabUooo cos422U= idV=?abr loIdlB内内 dr b0adr tr

48、dUooo sin2 麦克斯韦在总结前人成就的基础上麦克斯韦在总结前人成就的基础上,再结合他极再结合他极富创见的涡旋电场和位移电流的假说富创见的涡旋电场和位移电流的假说,建立起系统完建立起系统完整的电磁场理论整的电磁场理论,称为称为麦克斯韦方程组麦克斯韦方程组。 在变化电磁场情况下，在变化电磁场情况下， 12-8 麦克斯韦方程组麦克斯韦方程组涡旋电场涡旋电场空间任一点的电场：空间任一点的电场：产生电场产生电场) 1 () 1 (,DE)2()2(,DE)2() 1 (DDD)2() 1 (EEE变化磁场变化磁场电荷电荷静电场静电场=qo(自由电荷代数和自由电荷代数和)(涡旋电场的电力线是闭合曲

49、线涡旋电场的电力线是闭合曲线)电场的环流为电场的环流为电场的高斯定理为电场的高斯定理为slldsDdsDdsD)2()1(sdsD)1(sdsD)2(soqdsDllldlEdlEdlE)2() 1 (0dtdmsmldstBdtddlE内oq0在变化电磁场情况下，在变化电磁场情况下，空间任一点的磁场：空间任一点的磁场：则磁场的高斯定理为则磁场的高斯定理为(磁力线是闭合曲线磁力线是闭合曲线)传导电流传导电流(运动电荷运动电荷)位移电流位移电流(电场的变化电场的变化)产生磁场产生磁场)1()1(,HB)2()2(,HB)2()1(HHH)2()1(BBBssdB0磁场的环流为磁场的环流为llld

50、lHdlHdlH)2() 1 (ldlH) 1 (ldlH)2( selsdtDIdtdIl dH (传导传导电流的代数和电流的代数和)Idtde(位移位移电流的代数和电流的代数和)dstDs)(sedsD0I于是就得于是就得麦克斯韦方程组：麦克斯韦方程组： soqdsD smldstBdtddlE sdsB0 seldstDIdtdIdlH HBED ,麦克斯韦方程组的意义：麦克斯韦方程组的意义：(1)概括、总结了一切宏观电磁现象的规律。概括、总结了一切宏观电磁现象的规律。(2)预见了电磁波的存在。预见了电磁波的存在。变化的磁场激发电场变化的磁场激发电场变化的电场激发磁场变化的电场激发磁场

51、电磁场这样交替激发，就可以离开场源而在空间作电磁场这样交替激发，就可以离开场源而在空间作为一个整体传播开去，从而形成电磁波。为一个整体传播开去，从而形成电磁波。i 例题例题12-27 反映电磁场基本性质和规律的积分形式反映电磁场基本性质和规律的积分形式的的麦克斯韦方程组麦克斯韦方程组为为1.变化的磁场一定伴随有电场。变化的磁场一定伴随有电场。2.磁感应线是无头无尾的。磁感应线是无头无尾的。3.电荷总伴随有电场。电荷总伴随有电场。在下列描述后在下列描述后,写出对应的写出对应的方程方程序号序号 :(2)(3)(1)(1)(2)(3)(4) soqsdD smlsdtBdtdldE ssdB0 se

52、lsdtDIdtdIl dH 12-9 电磁波的波动方程电磁波的波动方程jxyzHzEy 设无限大平面上的电流密度设无限大平面上的电流密度: jy=Acos( t+ )。dtdl dEml 对对abcd:abcdEyEy+ dEydxl-Eyl+(Ey+dEy)ldtldxHdz)( ldxtHz tHxEzy dtdIl dHel 对对efgh:efghHzHz+ dHzdxljxyzHzEyabcdEyEy+ dEydxltHxEzoy Hzl-(Hz+dHz)ldtldxEdy)( tExHyz ldxtEy tHxEzy tExHyz xtHxEzy222222tEtxHyz 这表明这表明:电磁场以波的形式在空间传播电磁场以波的形式在空间传播,形成电形成电磁波。磁波。1 2222tExEyy2222tHxHzz)(cosxtEEoy )(cosxtHHoz 1.波速波速1 真空中：真空中： 可见可见,真空中电磁波的传播速度即为真空中电磁波的传播速度即为光速光速。这与实验。这与实验结果一致。这也表明结果一致。这也表明,光波光波就是在某一波段的就是在某一波段的电磁波电磁波。2.电场和磁场的周期、相位相同电场和磁场的周期、相位相同，且，且 HE 3.电磁波是横波电磁波是横波oo1 E，H的方向与传