自适应信号处理2

1、1LMSLMSKXKdLMS算法算法 最小均方算法，是对自适应线性组合时的特殊最小均方算法，是对自适应线性组合时的特殊的梯度估计算法，所以的梯度估计算法，所以LMS算法比牛顿和最陡算法比牛顿和最陡下降算法更受限制下降算法更受限制。算法特点：算法简单、容易计算算法特点：算法简单、容易计算 不需要额外的梯度估计和数据重复抽样不需要额外的梯度估计和数据重复抽样和希望响应和希望响应在每次迭代都是可利用的，则在每次迭代都是可利用的，则算法是最好的选择。算法是最好的选择。C.3 LMS算法算法如果自适应系统是一个自适应线性组合，且如果输入矢量如果自适应系统是一个自适应线性组合，且如果输入矢量2KTKkkW

2、Xd KXKWk2KE 2K K K K KKLKKKKLKKKKKKXWWWWWWW 22)(10212022 KKKXW C.3.1 LMS算法的导出算法的导出 对于线性组合自适应系统对于线性组合自适应系统是输入样本矢量，是输入样本矢量，是是次迭代的加权矢量。次迭代的加权矢量。的梯度较为困难，而直接以的梯度较为困难，而直接以作为作为的估计，的估计，的估计的估计估计估计并以此得到梯度并以此得到梯度3KKKWW 1 KKKXW2 LMS 利用这种简单的梯度估计，可以导出类似最陡下降的自适应算法，利用这种简单的梯度估计，可以导出类似最陡下降的自适应算法，即即 此即为此即为Widrow-Hoff

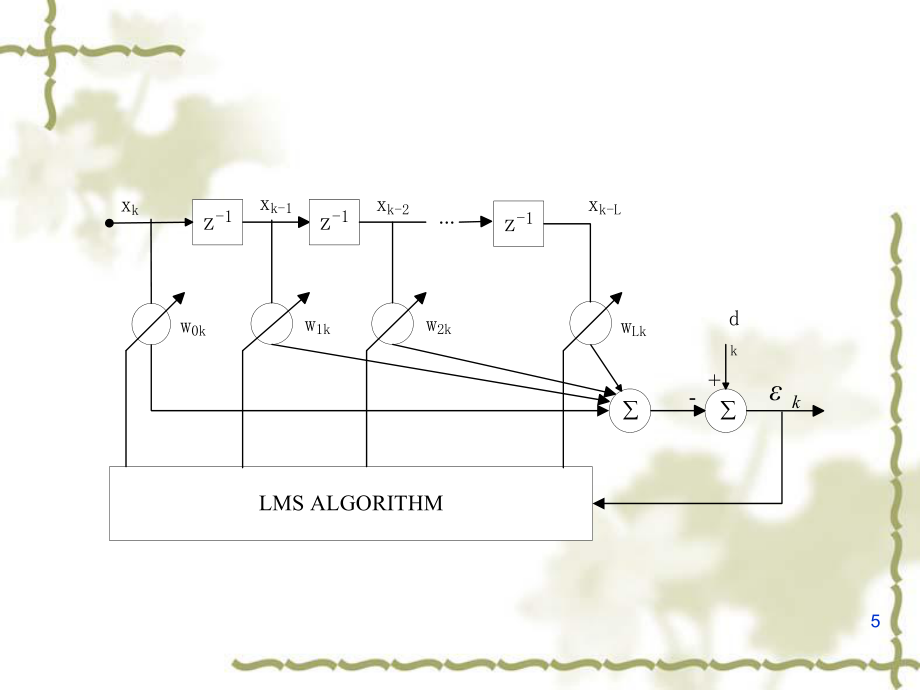
3、算法，其中算法，其中仍是收敛因子。仍是收敛因子。4vLMS实现算法的实际系统中不需要平方、平均或微分，因而实现算法的实际系统中不需要平方、平均或微分，因而这种系统具有简单和高效的优点，这种系统具有简单和高效的优点，v梯度矢量的每一分量是由单一数据取样获得，而与加权矢量梯度矢量的每一分量是由单一数据取样获得，而与加权矢量无关。无关。v 由于每次迭代中的加权矢量值的变化是根据粗略的梯度估计，由于每次迭代中的加权矢量值的变化是根据粗略的梯度估计，所以自适应过程是不准确的，它并不遵循在性能表面上的真所以自适应过程是不准确的，它并不遵循在性能表面上的真实的最陡下降曲线，且没有经过平均，梯度中包含有大量噪

4、实的最陡下降曲线，且没有经过平均，梯度中包含有大量噪声。声。v梯度估计噪声在自适应过程中将随时间而衰减，这种作用相梯度估计噪声在自适应过程中将随时间而衰减，这种作用相当于低通滤波器。当于低通滤波器。5z-1z-1z-1.xkxk-1xk-2xk-Lw0kw2kw1kwLkdkk+-LMS ALGORITHM6C.3.2 加权矢量的收敛性加权矢量的收敛性LMS2KE LMSWWK K 2KKKXEE 2WXXXdETKKKK )(2)(2dxdxRRWRWR K 算法主要关心的是对使算法主要关心的是对使最小的最佳加权矢量解的收敛性。最小的最佳加权矢量解的收敛性。算法的收敛性，先证明梯度估计的无偏

5、性算法的收敛性，先证明梯度估计的无偏性时，梯度估计时，梯度估计的期望值的期望值因此因此是真实梯度是真实梯度的无偏估计。的无偏估计。为检验为检验即当加权矢量保持为常数，即当加权矢量保持为常数，7KKKKXWW21 KW 1 KXKWKXKWEdxRRW1* 21KKKKXEWEWE )(2KTKKKWXEXdEWE KWKX 21KKKKKWREXdEWEWE *2)2(RWWERIK 将将用到最陡下降算法中，即用到最陡下降算法中，即加权矢量加权矢量仅仅是过去输入矢量仅仅是过去输入矢量的函数。的函数。独立于独立于 对于满足上述条件的平稳输入过程，在足够数目的迭代后加权矢量对于满足上述条件的平稳输

6、入过程，在足够数目的迭代后加权矢量可以证明是收敛于维纳最佳解可以证明是收敛于维纳最佳解 利用前述假设，利用前述假设，与与相互独立，则相互独立，则假设连续的输入矢量是在时间上相互独立的，则假设连续的输入矢量是在时间上相互独立的，则K 8)21(0VEVEKK K121 i 01max 经过座标位移和旋转至主轴系统，则有经过座标位移和旋转至主轴系统，则有 当无边界的增加当无边界的增加由前节推导可知，当且仅当由前节推导可知，当且仅当 或或时可以保证收敛。时可以保证收敛。加以限制，以使加权矢量的平均值收敛到加以限制，以使加权矢量的平均值收敛到的范围内，的范围内，的大小决定了自适应的速度和加权矢量中的大

7、小决定了自适应的速度和加权矢量中时，期望加权矢量到达最佳解。时，期望加权矢量到达最佳解。由此，对调节因子由此，对调节因子在在最佳加权矢量。最佳加权矢量。的噪声。的噪声。 9max R irt maxRtr R)1(2nrELRt inPL)1( 10Rtr PinL)1(10 R不可能大于不可能大于的对角元素之和，即的对角元素之和，即的对角元素之和的对角元素之和因此，加权矢量均值的收敛条件为：因此，加权矢量均值的收敛条件为：横向滤波器横向滤波器信号功率的估计要比估计信号功率的估计要比估计实际上由于噪声起伏，在收敛时会造成额外的均方误差。实际上由于噪声起伏，在收敛时会造成额外的均方误差。对于横向

8、自适应滤波器，对于横向自适应滤波器，一般形式一般形式的特征值容易得多。的特征值容易得多。10 nmseT nmse nnmse 41 mseT )1()1(2 LNLNTmsemseLMS算法是基于单个数据输入观测，故用输入样本表示算法是基于单个数据输入观测，故用输入样本表示的时间常数的时间常数与与相同，即相同，即对于一般自适应算法，每次迭代所需的数据样本用以测量对于一般自适应算法，每次迭代所需的数据样本用以测量每一个梯度分量，自适应时间常数定义为每一个梯度分量，自适应时间常数定义为。 nmsenmseT LMS算法自适应学习曲线是若干指数函数之和，其时间常数算法自适应学习曲线是若干指数函数之

9、和，其时间常数11Kmin6mseT120mseT典型的学习曲线典型的学习曲线12C.3.3 梯度估计对自适应过程的影响梯度估计对自适应过程的影响v理论上，自适应算法中要求精确地测量梯度矢量，以便在每次理论上，自适应算法中要求精确地测量梯度矢量，以便在每次迭代中使用。迭代中使用。v在大多数应用中，精确测量是得不到的，而只能根据有限的样在大多数应用中，精确测量是得不到的，而只能根据有限的样本进行估计，这样的估计是有噪声的，因此可以看作实际梯度本进行估计，这样的估计是有噪声的，因此可以看作实际梯度加上噪声。加上噪声。v以有噪声的梯度估计为基础的自适应过程将使加权矢量解被噪以有噪声的梯度估计为基础的

10、自适应过程将使加权矢量解被噪声污染，并导致性能上的损失。声污染，并导致性能上的损失。v有噪声梯度估计对收敛性能的影响程度随所采用的自适应算法有噪声梯度估计对收敛性能的影响程度随所采用的自适应算法不同而不同。不同而不同。13 由于每次迭代中的梯度估计是有噪声的，所以其加权轨迹由于每次迭代中的梯度估计是有噪声的，所以其加权轨迹是抖动的，也就是说，它们不是一直沿着真实的梯度方向下是抖动的，也就是说，它们不是一直沿着真实的梯度方向下降，收敛过程是不确定的。降，收敛过程是不确定的。w0w10w*w14KWW KNK KKKKKNRVN 2K KWW KKKWW 1 *WKKKVV 1 )2(KKKNRV

11、V KKNVRI )2( 在最陡下降法中，在最陡下降法中，设在设在K次迭代中，即次迭代中，即时梯度估计时梯度估计（L+1维矢量）维矢量）为为为为时的真实梯度时的真实梯度 座标平移到座标平移到处处 则梯度估值则梯度估值噪声矢量为噪声矢量为15VQVQVT1 KKNQN1 KKNQN KKKNQVQRVQ )21(1KKKNVV )21(111001)2()21( nKnKnKKNIVV max10 KV K10)2( nKnnKNIV 座标旋转座标旋转 迭代可得迭代可得 若若满足收敛稳定条件，即满足收敛稳定条件，即则则 第一项趋于零，则第一项趋于零，则时的稳态解为时的稳态解为 这是最陡下降法梯度

12、噪声对加权矢量稳态解的影响。这是最陡下降法梯度噪声对加权矢量稳态解的影响。16covKV covTKKKVVEV 21 )21()21(KKTKKVNEVVE )21(2TKKKKNNENVE covcov21 22KKNV cov4cov12KKNV 协方差协方差为为 17)()(21 vvv)(covTKKKNNEN QNNEQTKK)(1 QEQTKKKK)()(1 INNK2min2cov QVQVKKcovcov1 2122min4)( NRR 若设梯度估计为若设梯度估计为 由于梯度估值的取样相互独立由于梯度估值的取样相互独立，故估值的误差也相互独立且故估值的误差也相互独立且具有相同

13、的方差。具有相同的方差。 当自适应过程收敛于最佳加权矢量附近时，可近似得到梯度噪当自适应过程收敛于最佳加权矢量附近时，可近似得到梯度噪声的协方差为声的协方差为 )()(21(var(var41var2222 vvNvvv18 NkrkrN11 rkrrEE 424432122 de222 kE222)(varrrrrrEE NkNlrrlkEN1122)(1 lkEElkEErrlrkrrkrlk,)(222 NNNNNrrrrrr2222222)(1var NNN2422422var 其中由其中由 故故19KKkKNVIV )2(1101)2( nKnnKNIV cov)1(4)(cov21

14、KKNV INNK22mincov QVQVKKcovcov1 )1(4)(2212min NR 在牛顿算法时，类似地有在牛顿算法时，类似地有迭代可得迭代可得 K时的稳态解为时的稳态解为 20LMSKKKN 0 K*WWKKKKKXN 2 4cov2TKKKTKKKXXENNEN *WW 2K KXRXXEENTKKKKmin244cov min11114cov)(EcovcovQNQNQNQNQNKTKKKK算法时的梯度估计噪声对自适应过程的影响算法时的梯度估计噪声对自适应过程的影响 当当，当当， 与与近似不相关，则近似不相关，则 座标旋转座标旋转（1）加权矢量解中的噪声）加权矢量解中的噪声

15、21KKKNVV )21(1cov111 KKKVVEVcov)(4cov12KKNV 12min)( 1 IVKmin1mincov IQVQVKKmin1covcov （2）噪声对加权矢量解起伏的影响）噪声对加权矢量解起伏的影响因为因为，近似有，近似有22C.3.4 失调失调KVmin min minKTKKRVVEEexcessMSE 20nknLnKKVEVVEexcessMSE 在自适应过程中，如果不考虑噪声的影响，那么自适应算在自适应过程中，如果不考虑噪声的影响，那么自适应算法将使加权矢量收敛于均方误差最小值上的一个稳态解，并且法将使加权矢量收敛于均方误差最小值上的一个稳态解，并且

16、的协方差将等于零，均方误差的协方差将等于零，均方误差 但在实际自适应过程中，梯度估计噪声的存在使得稳态加但在实际自适应过程中，梯度估计噪声的存在使得稳态加权矢量解在最小点附近随机地变化，即在权矢量解在最小点附近随机地变化，即在“碗的侧壁上爬行碗的侧壁上爬行”，结果使得存在附加的均方误差，而且结果使得存在附加的均方误差，而且的稳态值大于的稳态值大于 定义附加均方误差为定义附加均方误差为此式只适用于自适应瞬变结束之后的稳态过程情况。此式只适用于自适应瞬变结束之后的稳态过程情况。2324 0011112nmmKmTnKnNrNrEexcessMSE 21 r 011102nmKTnKmmnNNErr

17、 011122nnKTnKnNNEr 0,111 nKTnKNNEnm 0122nKTKnNNEr LmmKmnEr021221 LmmN02min21)1(4 v 牛顿法牛顿法 25avLmmL 1)1(10min2 avP 21 )1( LNTmse NPLexcessMSEavav81)1(min mseavavPTL81)1(min2 令令, 而而 ，可近似求得可近似求得 扰动扰动 26 011102)2(nmKmnTnKmNINEexcessMSE LmmavNPexcessMSE0min114 nn 21 nnmseLNT )1( nmssenTLN 2)1( avmsseavTL

18、N 12)1( avmseTPLexcessMSE 18)1(min2 v 最陡下降法最陡下降法类似可得类似可得又又,可得可得 在稳态缓慢收敛时，在稳态缓慢收敛时，很小而很小而很大，故近似可得很大，故近似可得 27IVEVVEVLnnKTKKKmin02cov 20nknLnKTKVEVVEMSEexcess min0minRtrnLn 4141RtLrnnmse avmsenmsenLnrLRt 1411410avmseLexcessMSE 14)1(minv LMS算法算法 由由 28Mmin excessMSEM mseavavPTLM81)1(2 avmseTPLM 18)1(2avm

19、seLM 141另一种测量实际性能和最佳性能之差的量称为误调另一种测量实际性能和最佳性能之差的量称为误调，定义为，定义为牛顿法牛顿法最陡下降法最陡下降法LMS算法算法 结论：结论：1. LMS算法失调较小，且随加权数线性增加，自适应速度更快；算法失调较小，且随加权数线性增加，自适应速度更快；2. 愈大，失调愈大，收敛快；愈大，失调愈大，收敛快； 愈小，失调愈小，收敛慢。愈小，失调愈小，收敛慢。29C.3.5 LMS自适应递归滤波器自适应递归滤波器 自适应横向滤波器结构简单、易于实现，但为达到较好性能，自适应横向滤波器结构简单、易于实现，但为达到较好性能，需高阶需高阶FIR滤波，计算量较大。滤波

20、，计算量较大。递归结构的递归结构的IIR滤波器能够降低阶数，减少计算量，并具有锐截滤波器能够降低阶数，减少计算量，并具有锐截止等性能。止等性能。nkLnnnkLnnkybxay 10一般地，递归滤波器表示为一般地，递归滤波器表示为30自适应递归滤波器的原理结构自适应递归滤波器的原理结构31 LnnnzazA0)( LnnnzbzB1)()(1)()(zBzAzH 设设传输函数传输函数自适应递归滤波器存在二个缺点：自适应递归滤波器存在二个缺点：1. 在自适应过程中，极点可能移到单位圆外，导致滤波器不稳定；在自适应过程中，极点可能移到单位圆外，导致滤波器不稳定；2. 性能曲面超过二次，有局部极小点

21、，搜索最小点复杂。性能曲面超过二次，有局部极小点，搜索最小点复杂。32 TLkkkLkkkKyyyxxxU ,11 TLkkkLkkkKbbbaaaW,2110 KTKKKKKUWdYd KKKKKKWW 2)(2 TLKKKKLKKKKKbbaa ,210TLKKKKLKKKKKbybyayay ,210定义定义 信号矢量信号矢量 加权矢量加权矢量则则LMS算法：算法：33 Llnlklnknknkaybxay1 Lllknlnkbx1, Llnlklnknknkbybyby1 Lllknlnkby1, nknk ,kkyx ,)(1)(zBzzHknn TLkkLkkKK ,210 令令分

22、别相对分别相对的传输函数，的传输函数，则则 Ln 034KKKMWW 1 LdiagM ,1 0 nkb加权矢量的迭代关系加权矢量的迭代关系 递归自适应递归自适应LMS算法在算法在 即非递归自适应即非递归自适应LMS算法算法 自适应自适应IIR滤波器等效双输入滤波器等效双输入自适应自适应FIR滤波器，性能有类似滤波器，性能有类似35C.3.6 LMS自适应格型滤波器自适应格型滤波器kxLkkxx 1 LlllfzbzH11)(Lkx 1 Lkkxx LllLlLbzbzzH1)(格型结构格型结构前向预测：前向预测：用其前用其前L个采样个采样来预测，输出前向预测误差。来预测，输出前向预测误差。后

23、向预测：后向预测：用其后用其后L个采样个采样来预测，输出后向预测误差。来预测，输出后向预测误差。传输函数传输函数传输函数传输函数36+z-1+z-1.z-1+f0(n)f1(n)f2(n)fm-1(n)fm(n)g0(n)g1(n)g2(n)gm(n)r1r1r2r2rmrmxn格型结构：由若干个格型单元级联而成格型结构：由若干个格型单元级联而成可以证明：自适应递归滤波器的一般形式可以转换为格型结构。可以证明：自适应递归滤波器的一般形式可以转换为格型结构。37)1()()(11 ngrnfnfmmmmnxnf )(0)1()()(11 ngnfrngmmmmnxng )(0)()()(111z

24、GzrzFzFmmmm )()(0zXzF )()()(111zGzzFrzGmmmm )()(0zXzG 在在LMSLMS自适应格型滤波器中，采用相同的前后向反射系数自适应格型滤波器中，采用相同的前后向反射系数r rm m后向预测误差后向预测误差Z变换变换，前向预测误差前向预测误差定义在定义在n时刻、第时刻、第m级格型单元中级格型单元中38)()()()()(0zFzFZXzFzAmmm )()()()()(0zGzGZXzGzBmmm )()()(111zBzrzAzAmmmm 1)(0 zA)()()(111zBzzArzBmmmm 1)(0 zB前向滤波器传输函数前向滤波器传输函数 后

25、向滤波器传输函数后向滤波器传输函数 得到得到，即格型结构表示即格型结构表示39)(ngm)()(1 zAzzBmmm )()(22ngEnfEmm 可以证明：可以证明：（2）格型滤波器只对新增一级滤波系数独立调节使输出均方误差）格型滤波器只对新增一级滤波系数独立调节使输出均方误差 最小，而不需调节前面各级系数，相对横向滤波器各级系数最小，而不需调节前面各级系数，相对横向滤波器各级系数 联合调整，具有更快的收敛性能；联合调整，具有更快的收敛性能；，互为反转，即若前向传递函数零点在单位，互为反转，即若前向传递函数零点在单位圆内，则后向传递函数零点在单位圆外；圆内，则后向传递函数零点在单位圆外；，即

26、前后向预测均方残差恒等。，即前后向预测均方残差恒等。（1）各级后向预测误差）各级后向预测误差 正交，即前后级之间互相解耦，正交，即前后级之间互相解耦，系统最小化可转化为一系列独立的每一级局部最小化问题；系统最小化可转化为一系列独立的每一级局部最小化问题；（3）（4）40 0)()(22 mmmmrngErnfE)()()1()(22KgKfKEmmm 考虑使前向和后向预测误差的均方值同时最小的滤波器考虑使前向和后向预测误差的均方值同时最小的滤波器设计准则，即设计准则，即定义误差函数定义误差函数LMS自适应格型滤波器自适应格型滤波器 是前向和后向预测误差的加权，是前向和后向预测误差的加权，104

27、1)()()(KEKnWKEmnm )(nW)(nEm0)()( nrnEmm)(nrm加权误差函数加权误差函数为权系数，且满足为权系数，且满足最小，则最小，则即可求得反射系数即可求得反射系数的最佳值的最佳值欲使欲使00 ，nW(n)00 ，nW(n)42)(/ )()(1nDnCnrmmm )1()()0()1()(11 ngnfWnCnCmmmm)1()1()()0()1()(2121 ngnfWnDnDmmmm )(nW1111)( zzW 1 01 11 Makhoul &Cosell最佳表达式：最佳表达式：其中其中选择加权函数选择加权函数使其使其Z变换变换 称为衰落因子，称为

28、衰落因子，时自适应快，时自适应快， LMS自适应格型算法较自适应格型算法较Widrow-Hoff的的LMS算法复杂，算法复杂，但收敛速度较快。但收敛速度较快。时自适应慢。时自适应慢。43C.3.7 归一化LMS算法KKTKXWd1 KKKWWW 11KKKKXXW 211 l 归一化归一化LMS滤波器与一般滤波器与一般LMS滤波器结构相同，收敛更快滤波器结构相同，收敛更快l 归一化归一化LMS滤波器可减小梯度估计噪声放大对性能的影响滤波器可减小梯度估计噪声放大对性能的影响归一化归一化LMS滤波器设计要求：滤波器设计要求：（1）使加权向量的变化）使加权向量的变化的范数最小的范数最小（2）满足约束条件）满足约束条件根据最小均方准则，得到根据最小均方准则，得到KKKKKXWW 1是收敛因子常数是收敛因子常数XKK ,2 引入收敛因子常数引入收敛因子常数 ，则有，则有其中其中44C.3.8 LMS滤波器的统计特点KKKKXWW21 102KnKTnnKTKKXXXWY l输入向量输入向量X1，X2，XK相互统计独立相互统计独立lK时刻输入向量时刻输入向量XK与过去的希望响应与过去的希望响应d1，d2，dK-1