球的习题课(成稿)与向量法解立体几何中的探索性问题与翻折问题

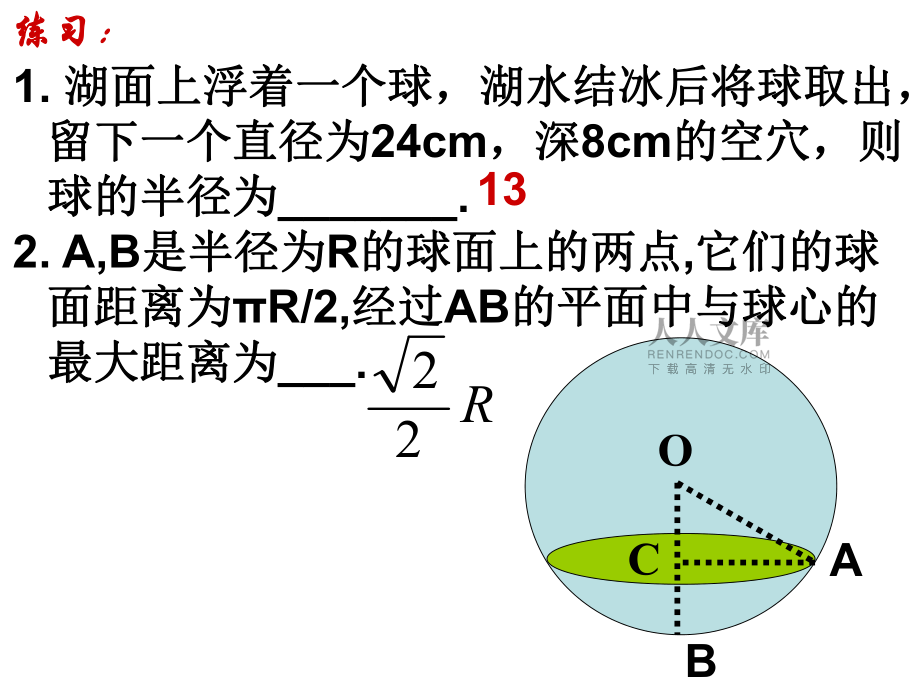
1、球的习题课OCAB练习：练习：1. 湖面上浮着一个球，湖水结冰后将球取出，湖面上浮着一个球，湖水结冰后将球取出，留下一个直径为留下一个直径为24cm，深，深8cm的空穴，则的空穴，则球的半径为球的半径为_.2. A,B是半径为是半径为R的球面上的两点的球面上的两点,它们的球它们的球面距离为面距离为R/2,经过经过AB的平面中与球心的的平面中与球心的最大距离为最大距离为_.R22133. 地球半径用地球半径用R表示表示,在赤道上有在赤道上有东经东经 和西经和西经 的的A,B两两点点,试求试求A,B两点间的球面距离两点间的球面距离.01450125OABR2OO1AB2.设地球的半径为设地球的半径

2、为R，地球上地球上A、B两点都在两点都在北纬北纬45的纬线上，的纬线上，A、B两点的球面距离两点的球面距离是是 , A在东经在东经200， 求求B点的位置。点的位置。R3变式练习变式练习 1. 甲乙两地在甲乙两地在北纬北纬450圈上，圈上，且它们分别位且它们分别位于东经于东经690与西经与西经210 ，求甲乙在，求甲乙在北纬北纬45圈上的劣弧长与其球面距离之比。圈上的劣弧长与其球面距离之比。4:23例例3.在半径为在半径为1的球面上有三点的球面上有三点A,B,C, A和和B, A和和C的球面距离都为的球面距离都为 ,B和和C的球面距的球面距离为离为 ,过过A,B,C三点作截面三点作截面.求球心

3、到截面求球心到截面的距离的距离.23ABCO 变式练习变式练习 已知已知A,B,C是半径为是半径为R的球面上三点的球面上三点, , 试求试求RACBCAB22OABCVCOABP24810R结论：结论：. .长方体的外接球直径长方体体对角线长方体的外接球直径长方体体对角线. .正方体的内切球直径正方体棱长正方体的内切球直径正方体棱长. .棱长为棱长为a a的正四面体的内切球半径的正四面体的内切球半径 外接球半径外接球半径a46a126 1.两个球的体积之比是：，两个球的体积之比是：，求它们的表面积之比求它们的表面积之比_. 2. 在球面上有在球面上有4个点个点P,A,B,C,若若PA, PB,

4、 PC两两垂直两两垂直,且且PA=PB=PC=a,则这个球的表面积为则这个球的表面积为_.23 a变式练习变式练习4：93一个四面体的所有棱长都为，一个四面体的所有棱长都为，四个顶点在同一个球面上，则此球表面四个顶点在同一个球面上，则此球表面积为积为（高考）（高考） 233463MNCEA 4.一个正方体内接于球一个正方体内接于球,过球心过球心O作作一个截面一个截面,则截面可能的图形是则截面可能的图形是( ) A.(1)(3) B.(2)(4) C.(1)(2)(3) D.(2)(3)(4).(1) (2) (3) (4)C二、球与多面体的接、切定义1：若一个多面体的各顶点都在一个球的球面上，

5、 则称这个多面体是这个球的内接多面体， 这个球是这个多面体的外接球。定义2：若一个多面体的各面都与一个球的球面相切， 则称这个多面体是这个球的外切多面体， 这个球是这个多面体的内切球。一、复习球体的体积与表面积343VR 球球24SR 球球面面解决“接切”问题的关键是画出正确的，把空间“接切”转化为平面“接切”问题：有三个球：有三个球,一球切于正方体的各面一球切于正方体的各面,一球切一球切于正方体的各侧棱于正方体的各侧棱,一球过正方体的各顶点一球过正方体的各顶点,求求这三个球的体积之比这三个球的体积之比.画出正确的截面：(1)中截面；(2)对角面找准数量关系21ar aaaa2ar222aa2

6、ar2331. 已知长方体的长、宽、高分别是 、 、1 ，求长方体的外接球的体积。35A1AC1CO变题：2. 已知球O的表面上有P、A、B、C四点，且PA、PB、PC两两互相垂直，若PA=PB=PC=a，求这个球的表面积和体积。沿对角面截得：ACBPO半球的半径为R，一正方体的四个顶点在半球的底面上，另四个顶点在球面上，求正方体的棱长：正四面体：正四面体ABCD的棱长为的棱长为a，求，求其内切球半径其内切球半径r与外接球半径与外接球半径R.：若正四面体变成正三棱锥，方法：若正四面体变成正三棱锥，方法是否有变化？是否有变化？1、内切球球心到多面体各面的距离均相等，外接球球心到多面体各顶点的距离

7、均相等2、正多面体的内切球和外接球的球心重合3、正棱锥的内切球和外接球球心都在高线上，但不重合4、基本方法：构造三角形利用相似比和勾股定理5、体积分割是求内切球半径的通用做法O1ABEO O1ABEO 1例 、正三棱锥的高为 1，底面边长为内有一个球与四个面都相切，求棱锥的全面积和球的表面积。62232过侧棱AB与球心O作截面( 如图 )在正三棱锥中，BE 是正BCD的高O1 是正BCD的中心，且AE 为斜高62BC 21 EO3AE 且且 26243362213S 全全3669 O1ABEO O1ABEO 123例 、正三棱锥的高为 1，底面边长为内有一个球与四个面都相切，求棱锥的全面积和球

8、的表面积。62设内切球半径为 r，则 OA = 1 r作 OF AE 于 FF Rt AFO Rt AO1E 312rr 26 r 6258S球球O1ABEO 13233sin 36cos 在 Rt AO1E 中 sincos12tan23 在 Rt OO1E 中26OO1 6258S球球例 、正三棱锥的高为 1，底面边长为内有一个球与四个面都相切，求棱锥的全面积和球的表面积。62 1624331V2BCDA 26r 6258S球球例 、正三棱锥的高为 1，底面边长为内有一个球与四个面都相切，求棱锥的全面积和球的表面积。62OAB CD设球的半径为 r，则 VA- BCD = VO-ABC + VO- ABD + VO-ACD + VO-BCD32 全全Sr31 r3223 内切球内