大学物理(下)40学时期末复习PPT课件

1、大学物理大学物理( (下下)40)40学时学时期末复习期末复习2一、理想气体的状态方程一、理想气体的状态方程pVRT（91）pnkT（92）8.31/(mol K)RJ普适气普适气体常量体常量molAMNNM气体的气体的摩尔数摩尔数23-16.02 10 molAN 阿伏伽德罗常量阿伏伽德罗常量NnV单位体积内的分子数，单位体积内的分子数，分子数密度分子数密度231.38 10J/KARkN玻尔兹曼常量玻尔兹曼常量3二、理想气体压强和温度公式二、理想气体压强和温度公式212ktm分子的平均平动动能分子的平均平动动能理想气体的理想气体的压强公式压强公式理想气体的理想气体的温度公式温度公式2kt1

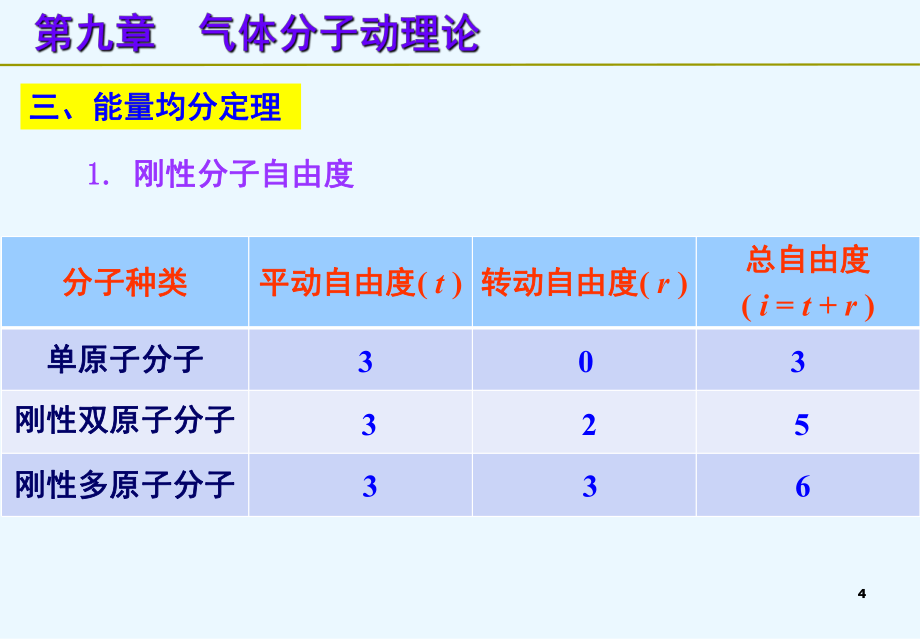
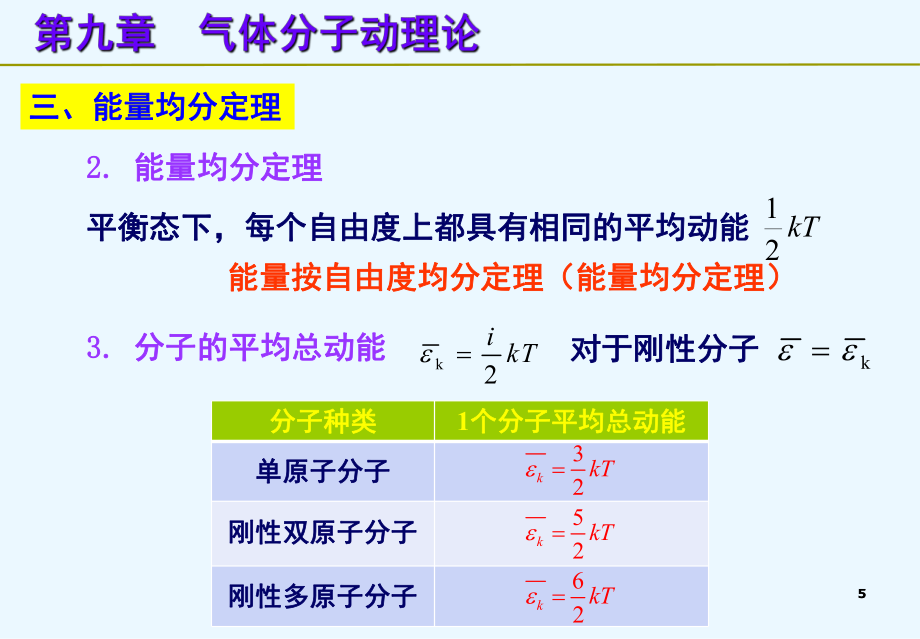
2、322mkTkt23pn4 4三、能量均分定理三、能量均分定理分子种类分子种类平动自由度平动自由度( t ) 转动自由度转动自由度( r )总自由度总自由度( i = t + r )单原子分子单原子分子刚性双原子分子刚性双原子分子刚性多原子分子刚性多原子分子 3 0 3 3 2 5 3 3 61. 1. 刚性分子自由度刚性分子自由度5 5三、能量均分定理三、能量均分定理平衡态下，每个自由度上都具有相同的平均动能平衡态下，每个自由度上都具有相同的平均动能 kT21能量按自由度均分定理（能量均分定理）能量按自由度均分定理（能量均分定理）2. 2. 能量均分定理能量均分定理3. 3. 分子的平均总动

3、能分子的平均总动能k2ikTk对于刚性分子对于刚性分子分子种类分子种类1个分子平均总动能个分子平均总动能单原子分子单原子分子刚性双原子分子刚性双原子分子刚性多原子分子刚性多原子分子32kkT52kkT62kkT6 6三、能量均分定理三、能量均分定理4. 4. 理想气体的内能理想气体的内能1 1个个气体分子的内能气体分子的内能0()2AiENkT一定质量理想气体的内能一定质量理想气体的内能mol2MiERTM1 1mol 理想气体的内能理想气体的内能2ikT2iRT分子种类分子种类理想气体的内能理想气体的内能单原子分子单原子分子刚性双原子分子刚性双原子分子刚性多原子分子刚性多原子分子mol32M

4、ERTMmol52MERTMmol62MERTM7 7四、速率分布律四、速率分布律d( )dNfN表示表示速率分布在速率分布在 附近单位速率区间内的分附近单位速率区间内的分子数占总分子数的百分比子数占总分子数的百分比，称，称速率分布函数速率分布函数。 速率分布在速率分布在 间隔内的分子数间隔内的分子数dN 占总分子数占总分子数N的百分比的百分比d d( )dNfN表示表示 1归一化条件归一化条件0( )df 21( )df速率分布在速率分布在 间隔内的分子数占总分子数的百分比可表示为间隔内的分子数占总分子数的百分比可表示为12 21( ), ( ), ( )ggg( )( ) ( )doggf

5、其平均值为其平均值为如某个物理量是关于速率如某个物理量是关于速率 的函数的函数 ，如，如()g8 8四、速率分布律四、速率分布律三种统计速率三种统计速率2kTpm21.41molmolRTRTMM1.最概然速率（最概然速率（ ） p2.平均速率平均速率( )0( )df881.60molmolkTRTRTmMM2331.73molmolkTRTRTmMM3.方均根速率方均根速率( )2220( )df2（）p9 9五、气体分子的平均碰撞频率和平均自由程五、气体分子的平均碰撞频率和平均自由程1.1.平均碰撞频率平均碰撞频率22Zdn2.2.平均自由程平均自由程212Zd n22kTd pnkTp

6、 与分子的有效直径的平方、分子数密度成反比，与分子的有效直径的平方、分子数密度成反比，但与平均速率无关。但与平均速率无关。当温度一定时当温度一定时, ,平均自由程与气体压强成反比。平均自由程与气体压强成反比。1010312TTT温度温度，速率大的分子数，速率大的分子数同一气体不同温度下速率分布比较同一气体不同温度下速率分布比较( )fO3T2T1T2()pf1()pf2p3()pf1p3p同一温度下不同种气体速率分布同一温度下不同种气体速率分布比较比较312mmm分子质量越小，速率大的分子数分子质量越小，速率大的分子数越多越多2kTpm( )fO3m2m1m1p2p3p1111解解 (1) 氢

7、气是双原子分子，自由度氢气是双原子分子，自由度i = 5，平动自由度，平动自由度t = 376kt331.1 106.6 10 (J)55EEAmolMNNM621ktktk23A3mol6.6 108.24 10(J)2.66 6.02 102 10tEEMNNMkt32kT21kt2322 8.24 10398(K)33 1.38 10Tk平均平动动能总和平均平动动能总和 (2) 容器内氧气的摩尔分子数为容器内氧气的摩尔分子数为 分子的平均平动动能分子的平均平动动能 (3)71.1 10 JE 12P148. 3 体积为体积为V 的房间与大气相通，大气压强为的房间与大气相通，大气压强为p0

8、，开始时室内，开始时室内与室外温度均为与室外温度均为T0，现使室内温度降为，现使室内温度降为T，则房中气体内能的增量，则房中气体内能的增量是多少？摩尔数的增量是多少？是多少？摩尔数的增量是多少？解解 设初态房中气体质量为设初态房中气体质量为M0，末态质量为，末态质量为M，室内与大，室内与大气相通，故过程中压强不变气相通，故过程中压强不变00molmol022MMiiERTRTMM 0molmolMMMM （2）摩尔数的增量）摩尔数的增量000p Vp VRTRT0011p VRTT（1）内能的增量内能的增量000molMp VRTM初态初态00molmolMMRTRTMM0molMp VRTM

9、末态末态1213P148. 4 若对一容器中的刚性分子理想气体进行压缩，并同时对它若对一容器中的刚性分子理想气体进行压缩，并同时对它加热，当气体温度从加热，当气体温度从 升高到升高到 时，其体积减少为二分时，其体积减少为二分之一，求下列各量变化前后之比：之一，求下列各量变化前后之比：(1) 压强；压强；(2) 分子的平均动能；分子的平均动能；(3) 方均根速率。方均根速率。解解 (1) 根据理想气体状态方程根据理想气体状态方程 得得(2)13222111TVpTVp21 212 1273 177231(27327)pVTpV T027 C0177 C2221114503230022kkikTT

10、iTkT(3)22mol222111mol3450623300RTMTRTTM1414一、内能一、内能 功功 热量热量理想气体的内能理想气体的内能体积功体积功21dVVWp VddWp V热量热量mmolMQCTM,2V mmolmolMiMERTCTMM二、热力学第一定律二、热力学第一定律21QEEW2molMiR TME做功和热传递都可以改变系统内能。做功和热传递都可以改变系统内能。1515三、理想气体的等值过程三、理想气体的等值过程1.1.等体过程等体过程气体对外不做功气体对外不做功0W 21mol()2MiR TTM21VQEE2.2.等温过程等温过程1mol2lnpMRTMp2mol

11、1lnVMRTMV21dVTTVWQp V21mol1dVVMRTVMV内能保持不变内能保持不变0E3.3.等压过程等压过程气体对外做功气体对外做功 21()ppQEEW21dVpVWp V21()p VV21mol()MR TTM2121molmol()()2MiMR TTR TTMM21mol2()2MiR TTM1616三、理想气体的热熔三、理想气体的热熔mddQCT,mddVVQCT2iERT理想气体理想气体,mdd22ViiCRTRTddET,mddppQCT对理想气体对理想气体2121()()2PiQR TTR TT,m222piiCRRR,mVCR定义定义,m,m2pVCiCi比

12、热容比比热容比或或绝热比绝热比1.1.气体摩尔热熔气体摩尔热熔2.2.定体摩尔热熔定体摩尔热熔3.3.定压摩尔热熔定压摩尔热熔1717四、绝热过程四、绝热过程0Q 21,m21mol()()QVMWEECTTM 绝热过程方程：绝热过程方程：1pV常量21常量TV13pT常量1818过程方程过程方程功功热量热量内能增量内能增量等体等体过程过程等压等压过程过程等温等温过程过程绝热绝热过程过程pT常量VT常量pV 常量pV常量1VT常量,m21mol()VMECTTM,m21mol()VVMQCTTM21()pWp VV21mol()MR TTM,m21mol()ppMQCTTM,m21mol()V

13、MECTTM0VW 0E0Q 2mol1lnTVMWRTMV1mol2lnpMRTMp,m21mol()VMECTTM QWETTQW理想气体等值过程和绝热过程的有关公式理想气体等值过程和绝热过程的有关公式1pT常量1919五、循环过程五、循环过程 E=01212QQWW正循环正循环1WQ211QQ 逆循环逆循环12WQQ2212QQWQQ六、卡诺循环六、卡诺循环两个两个等温过程等温过程、两个、两个绝热过程绝热过程211cTT T1 1、T2 2分别是高温热源和低温热源的温度分别是高温热源和低温热源的温度212TTTc致冷系数致冷系数开尔文表述：开尔文表述：不可能制成一种不可能制成一种循环动作

14、循环动作的热机，只从的热机，只从单一热源单一热源吸取吸取热量，使之完全变成有用的功而热量，使之完全变成有用的功而不引起其他变化不引起其他变化。克劳修斯表述：克劳修斯表述：热量不可能热量不可能自动地自动地从低温物体传向高温物体。从低温物体传向高温物体。七、热力学第二定律七、热力学第二定律2020一、简谐振动的运动学一、简谐振动的运动学0cos()xAt简谐振动表达式简谐振动表达式0dsin()dxAtt 0cos()2At2202dcos()dxaAtt 20cos()At1.1.振幅振幅AAxA2.2.周期周期T (s)2 T3.3.频率频率 (Hz)12T2反映振动系统能量的多少反映振动系统

15、能量的多少4.4.位相位相决定振动物体运动状态决定振动物体运动状态0t5.5.初相初相0决定振动物体最初的运动状态决定振动物体最初的运动状态2121二、旋转矢量二、旋转矢量 结论：结论：旋转矢量的端点在旋转矢量的端点在x轴上投轴上投影点的运动，就表示影点的运动，就表示简谐运动简谐运动； 矢量端点的速度在矢量端点的速度在x轴上的投影等轴上的投影等于简谐振动的于简谐振动的速度速度； 矢量端点的向心加速度在矢量端点的向心加速度在x轴上的轴上的投影等于简谐振动的投影等于简谐振动的加速度加速度。xo0AtA0t0cos()xAtA旋转矢量旋转矢量2222三、相位关系三、相位关系20100若若则说振动则说

16、振动x2 2比振动比振动x1 1超前。超前。20100若若则说振动则说振动x2 2比振动比振动x1 1滞后。滞后。tOxtOxx2 2、x1 1振动同相位振动同相位2 k 0,1,2,k x2 2、x1 1振动反相位振动反相位21 k 0,1,2,k 两个重要特例两个重要特例同相位同相位 反相位反相位(， 2323四、振幅、初相位的确定四、振幅、初相位的确定00sinA 00cosxA0,A取决于初始条件取决于初始条件. .000,txx)(T, 决定于系统的固有属性决定于系统的固有属性. .000tanx2202oA x0(， 2424五、简谐振动的动力学五、简谐振动的动力学线性回复力线性回

17、复力Fkx 简谐振动的动力学方程简谐振动的动力学方程222d0dxxt1.1.弹簧振子弹簧振子km角频率角频率2mTk周期周期12km频率频率2.2.单摆单摆lg2lTg12gl3.3.复摆复摆mgbJ2JTmgb12mgbJ2525六、简谐振动的能量六、简谐振动的能量222p011cos ()22EkxkAt以弹簧振子为例以弹簧振子为例00cos()sin()xAtAt v22pk21AkAEEE2222k011sin ()22EmmAtv2201sin ()2kAt一个周期内，动能和势能的平均值一个周期内，动能和势能的平均值21142kpEEkAE2626七、简谐振动的合成七、简谐振动的合

18、成1.1.同方向、同频率同方向、同频率1110cos()xAt2220cos()xAtcos()xAt22222011102cos()AAAAA211011020220sincossitnancosAAAA20102 k 0 1 2, k ， ，(1)(1)同相同相 max12AAAA振动加强振动加强 2010(21)k 0 1, 2k ，(2)(2)反相反相 min12AAAA振动减弱振动减弱 2727七、简谐振动的合成七、简谐振动的合成2.2.同方向、不同频率同方向、不同频率拍频拍频 振幅变化的频率振幅变化的频率, , 单位时间内强弱变化的次数单位时间内强弱变化的次数 212T121T12

19、21( )2 cos()2A tAt2828一、机械波的产生和传播一、机械波的产生和传播1.1.产生条件：波源和弹性介质产生条件：波源和弹性介质2.2.分类：横波和纵波分类：横波和纵波横波：横波：介质中质元的振动方向和波的传播方向垂直介质中质元的振动方向和波的传播方向垂直。如绳波如绳波纵波：纵波：介质中质元的振动方向和波的传播方向平行。介质中质元的振动方向和波的传播方向平行。如声波如声波3.3.波面、波线、波前波面、波线、波前在各项同性的均匀介质中，波线和波面相互垂直。在各项同性的均匀介质中，波线和波面相互垂直。12T4.4.波速、波长和频率的关系波速、波长和频率的关系2929二、平面简谐机械

20、波的波动表达式二、平面简谐机械波的波动表达式0cos()xyAtu0cos2 ()txAT0cos 2xAt22,uTT 1、已知坐标原点、已知坐标原点O的振动表达式的振动表达式2、已知、已知x0处质点的振动表达式处质点的振动表达式00( , )cos()xxxy x tAtu注意：波速注意：波速u恒取正值。恒取正值。3030三、波的能量三、波的能量波动是能量传递的一种方式波动是能量传递的一种方式 。平均能量密度平均能量密度 22021d1AtwTwT能流密度（波的强度）能流密度（波的强度）2212PIwuA uS单位：单位：2/mW3131四、波的衍射和干涉四、波的衍射和干涉 当波在传播过程

21、中遇到障碍物时，其传播方向发生改变，能绕过当波在传播过程中遇到障碍物时，其传播方向发生改变，能绕过障碍物的边缘继续前进的现象障碍物的边缘继续前进的现象波的衍射波的衍射。 如果两列如果两列频率相同、振动方向相同、相位差恒定频率相同、振动方向相同、相位差恒定的波相遇，在交的波相遇，在交叠区域的某些位置上，振动始终加强，另在另一些位置上，振动始终叠区域的某些位置上，振动始终加强，另在另一些位置上，振动始终减弱或抵消，这种现象称为减弱或抵消，这种现象称为波的干涉波的干涉P1r2r2S1SP点的振动点的振动 120cos()yyyAt2221122cosAAAAA1211022001211022022s

22、in()sin()tan22cos()cos()rrAArrAA20102()波源波源相位相位差差波程差引波程差引起的相位起的相位差差21rr波程差波程差3232四、波的衍射和干涉四、波的衍射和干涉2010()22k (21)k 其它其它max122AAAAA干涉相长干涉相长min120AAAA干涉相消干涉相消2121AAAAA若若 ， A A1 1= =A A2 2= =A A 则则102022k (0,1,2,)k 即即(21)2k 即即(0,1,2,)k 14II0I3333五、驻波五、驻波 驻波驻波是由两列是由两列振幅相同振幅相同的相干波在同一条直线上的相干波在同一条直线上沿相反方向传

23、播沿相反方向传播时叠加而成的一种特殊干涉现象。时叠加而成的一种特殊干涉现象。cos 21x当当2(0,1,2,)4xkk 即即( )2A xA1. 1. 驻波特点驻波特点 (2 cos2c2os)xtyA振幅最大，振幅最大，波腹波腹2x波腹间距波腹间距( )0A x 振幅最小，振幅最小，波节波节2x波节间距波节间距cos 20 x当当(21) (0,1,2,)4xkk 即即振幅分布振幅分布 2) 12(2kxkx23434五、驻波五、驻波相位分布相位分布 驻波中同一分段驻波中同一分段( (两个相邻波节之间的所有各点，叫两个相邻波节之间的所有各点，叫一分段一分段) )内，内，具有相同的符号，因此

24、这些点具有相同的振动相位。在波节两边，符具有相同的符号，因此这些点具有相同的振动相位。在波节两边，符号相反，其振动相位相反。号相反，其振动相位相反。驻波的能量驻波的能量驻波不传播能量。驻波不传播能量。3535五、驻波五、驻波2. 2. 半波损失半波损失 当当反射点固定反射点固定时时, ,反射点反射点A A是波节是波节, ,反射波与与入射波在反射波与与入射波在A A点是反点是反相位的相位的, ,即有即有的相位突变的相位突变, ,由于由于的相位突变相当于波程差半个波长，的相位突变相当于波程差半个波长，故将入射波在反射时发生反相的现象称之为故将入射波在反射时发生反相的现象称之为“半波损失半波损失”

25、当反射点是当反射点是自由端自由端时时, ,反射点反射点A A是波腹是波腹, ,反射波与入射波在反射波与入射波在A A点是同点是同相位的相位的, , 没有没有相位突变相位突变. .产生半波损失的条件：产生半波损失的条件： 波从波从波疏波疏介质垂直入射到介质垂直入射到波密波密介质上，介质上，反射波反射波产生半波损失。产生半波损失。3636一、热辐射一、热辐射 任何物体在任何温度下都以电磁波的形式向外发射能量的行任何物体在任何温度下都以电磁波的形式向外发射能量的行为称为为称为热辐射热辐射。2.总辐射本领总辐射本领(辐出度辐出度)E(T)0( )( , )dE TeT 温度为温度为T 时，在单位时间内

26、从物体表面的单位面积上发出的波长在时，在单位时间内从物体表面的单位面积上发出的波长在 附近单位波长间隔内的辐射能量。附近单位波长间隔内的辐射能量。1.单色辐射本领单色辐射本领(辐出度辐出度)e(,T)3( W/m )单位：瓦单位：瓦/米米3 温度为温度为T 时，在单位时间内从物体表面的单位面积上发出的总辐射能时，在单位时间内从物体表面的单位面积上发出的总辐射能量量辐射总功率辐射总功率( )d( )SPE TSE T S2( W/m )单位：瓦单位：瓦/米米23737二、黑体辐射两个实验规律二、黑体辐射两个实验规律1.斯特藩斯特藩玻耳兹曼定律玻耳兹曼定律4( )E TT8245.67 10 W/

27、mK（）2.维恩位移定律维恩位移定律bTm32.898 10 m Kb三、普朗克能量子假设三、普朗克能量子假设0=h 能量子能量子 =n0 （n 取正整数，称为量子数）取正整数，称为量子数）346.626 10()hJ s普朗克常量普朗克常量3838三、光电效应三、光电效应（2） 饱和电流饱和电流 im01. 实验规律实验规律（1） 截止频率（红限频率）截止频率（红限频率）0（3） 遏止电压遏止电压从阴极逸出的光电子有初动能从阴极逸出的光电子有初动能212ammeU00()aUKK （4） 驰豫时间驰豫时间得到得到2012mmeKeK212mhmW2. 爱因斯坦光电效应方程爱因斯坦光电效应方程

28、3939四、光的波粒二象性四、光的波粒二象性h光子能量光子能量光子质量光子质量22hhmccchpm c光子动量光子动量2000(1 cos )2sin2hhm cm c 五、康普顿效应五、康普顿效应康普顿波长康普顿波长1202.426 10mchm c4040六、德布罗意波六、德布罗意波hmcE2hpm德布罗意公式德布罗意公式七、波函数七、波函数i-0( , )eEt pxx t 341.05 10J s2h约化普朗克常量约化普朗克常量自由粒子波函数自由粒子波函数1. 波函数的统计诠释波函数的统计诠释表示在表示在t 时刻时刻, 粒子在空间粒子在空间 处单位体积内出现的概率处单位体积内出现的概

29、率, 也称概率密度也称概率密度r2,r tr tr t 波函数的模方波函数的模方2. 波函数的波函数的标准标准条件：条件：单值、有限、连续单值、有限、连续3. 波函数的波函数的归一化归一化条件条件2,d1r tV4141八、不确定关系八、不确定关系九、薛定谔方程九、薛定谔方程2xxp 2Et 2222222( , )( , )( , )i2pr tEr tr tmxyzt含时薛定谔方程含时薛定谔方程 222222220pmrEErrxyz定态薛定谔方程定态薛定谔方程 222d20dpxmEExxx一维定态薛定谔方程一维定态薛定谔方程4242十、一维无限深势阱十、一维无限深势阱1. 1. 势能函数势能函数阱内阱内 （0 0 xa) ) 0pEx 阱外阱外 ( (x0 a) ) pEx 2. 2. 波函数波函数 2sin1,2,3,.0nnxxnxaaa（1 1）能量