第二章杆件的内力分析

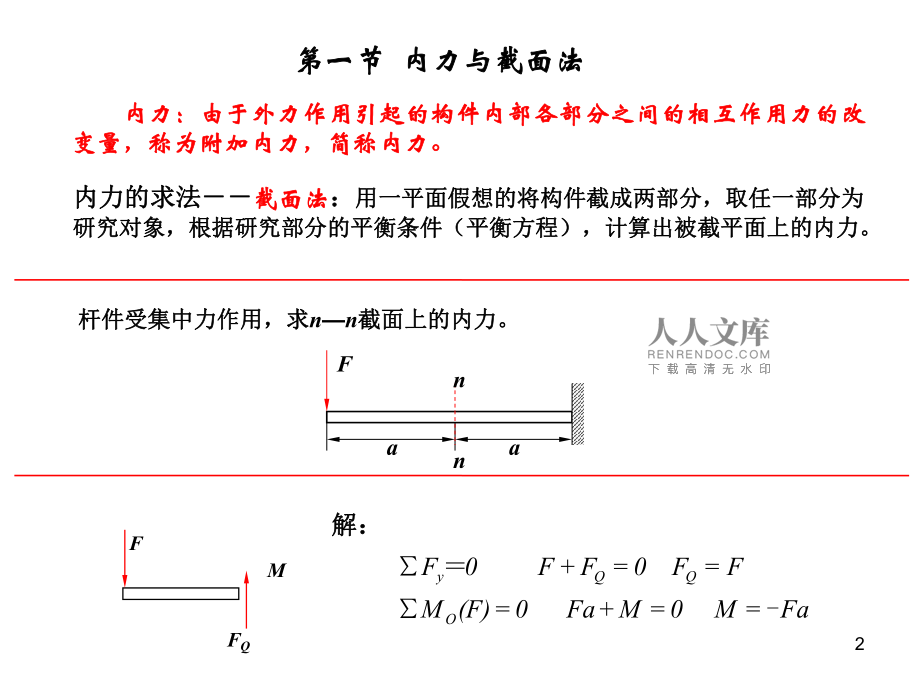
1、1本章重点本章重点第二章第二章 杆件的内力分析杆件的内力分析第一节第一节 内力与截面法内力与截面法第二节第二节 直杆轴向拉伸直杆轴向拉伸（压缩压缩）时的内力和内力图时的内力和内力图第三节第三节 圆轴扭转时的内力及内力图圆轴扭转时的内力及内力图第四节第四节 梁弯曲时的内力及内力图梁弯曲时的内力及内力图第五节第五节 复杂情况下的内力及内力图复杂情况下的内力及内力图杆件拉伸或压缩、扭转、弯曲时横截面上内杆件拉伸或压缩、扭转、弯曲时横截面上内力的计算和内力图的绘制力的计算和内力图的绘制. .2内力：内力：由于外力作用引起的构件内部各部分之间的相互作用力的改由于外力作用引起的构件内部各部分之间的相互作用

2、力的改变量，称为附加内力，简称内力。变量，称为附加内力，简称内力。内力的求法内力的求法截面法截面法：用一平面假想的将构件截成两部分，取任一部分为用一平面假想的将构件截成两部分，取任一部分为研究对象，根据研究部分的平衡条件（平衡方程），计算出被截平面上的内力。研究对象，根据研究部分的平衡条件（平衡方程），计算出被截平面上的内力。第一节第一节 内力与截面法内力与截面法杆件受集中力作用，求杆件受集中力作用，求nn截面上的内力。截面上的内力。aannFFQMF解：解：Fa M0MFa 0(F)MFF0FF 0FOQQy-=+=+3一、实例一、实例以拉、压为主要变形的构件称为杆。以拉、压为主要变形的构件

3、称为杆。第二节第二节 直杆轴向拉伸直杆轴向拉伸（压缩压缩）时的内力和内力图时的内力和内力图受力简图受力简图: :拉伸拉伸FF压缩压缩 作用在杆件上的作用在杆件上的外力外力的作用线与杆件的作用线与杆件轴线轴线重合，杆件主要变形是重合，杆件主要变形是沿轴线沿轴线方向的伸长或缩短方向的伸长或缩短。FF二、拉压杆的受力和变形特点：二、拉压杆的受力和变形特点：41 1、轴力、轴力FN：拉、压杆横截面上的内力：拉、压杆横截面上的内力FFmm0FF 0FNxFFN2 2、截面法、截面法求轴力求轴力或取截面右段：或取截面右段：三、拉、压杆的内力三、拉、压杆的内力轴力轴力FNFFNFFNFFN四、轴力正负号规定

4、：四、轴力正负号规定：使杆受拉时轴力为正、杆受时压为负。使杆受拉时轴力为正、杆受时压为负。五、五、轴力图轴力图：表示轴力沿杆件轴线的变化规律的图形。表示轴力沿杆件轴线的变化规律的图形。取取x轴平行于杆件轴线（作为基线），轴平行于杆件轴线（作为基线），y y轴为内力方向。轴为内力方向。轴力为正轴力为正(+)(+)FFN轴力为负轴力为负( () )xFN大部分情况下会省略坐标轴，作成这样的图：大部分情况下会省略坐标轴，作成这样的图：FN5 已知已知F1=10kN；F2=20kN； F3=35kN；F4=25kN;试求杆件的试求杆件的轴力并画出轴力图轴力并画出轴力图。F1F3F2F4ABCDF1F3

5、ABCDFN111F1F2ABCDFN222F1F3F2FN3ABC33011FF 0 FNxkNFFN1011解：各段的轴力。解：各段的轴力。AB段段kNFFFN10212BC段段0 0122FFFFNx003213FFFF FNxkNFFFFN253213CD段段轴力图轴力图101025FNxFN(kN)+_6 已知已知F1=10kN；F2=20kN； F3=35kN；F4=25kN; ;试画出图示杆件试画出图示杆件的轴力图的轴力图。解：解： 轴力图轴力图F1F3F2F4ABCD101025FN(kN)+_任一截面上的轴力，等于截面一侧所有外力的代数和。任一截面上的轴力，等于截面一侧所有外

6、力的代数和。7第三节第三节 圆轴扭转时的内力及内力图圆轴扭转时的内力及内力图汽车传动轴汽车传动轴一、实例一、实例汽车方向盘汽车方向盘丝锥攻丝丝锥攻丝以扭转为主要变形的杆件称为轴。以扭转为主要变形的杆件称为轴。 外力偶作用在垂直于杆件轴线的平面内外力偶作用在垂直于杆件轴线的平面内, ,使杆使杆件件的横截面绕轴的横截面绕轴线产生转动，圆轴表面的直线线产生转动，圆轴表面的直线( (母线母线) )变形后变为螺旋线。变形后变为螺旋线。 二、扭转轴的受力和变形特点：二、扭转轴的受力和变形特点：g g ：剪切角：剪切角j j ：扭转角：扭转角MeMej jg g母线母线螺旋线螺旋线81.1.直接计算直接计算

7、2.2.已知电机输出功率为已知电机输出功率为P（kW），转速为转速为 n（转（转/ /分钟）分钟）三、外力偶矩的计算三、外力偶矩的计算)mN(nP9549MM=Pee=四、扭矩和扭矩图四、扭矩和扭矩图截面法求扭矩截面法求扭矩exexMM 0M M M0扭矩正负规定扭矩正负规定( (右手螺旋法则右手螺旋法则) )：右手拇：右手拇指指向外法线方向为正指指向外法线方向为正(+)(+), ,反之负反之负(-)(-)。MemmMemmMeMxmmMxMe扭矩图扭矩图：表示扭矩沿轴线的变化规律的图形。表示扭矩沿轴线的变化规律的图形。9 已知转速已知转速n = 300r/min, ,主动轮主动轮A输入功率输

8、入功率PA=45kw , ,三个从动轮三个从动轮输出功率分别为输出功率分别为PB=10kw , PC =15kw ,PD =20kw 。绘制轴的扭矩图。绘制轴的扭矩图。解解: :计算外力偶矩：计算外力偶矩：mNM1432300/ )459549(AmNM318300/ )109549(BmNM637300/ )209549(DmNM477300/ )159549(C+_637N.m795N.m318N.m作业：作业：21(b), (d), 2(b), 310第四节第四节 梁弯曲时的内力及内力图梁弯曲时的内力及内力图起重机大梁起重机大梁一、实例一、实例火车轮轴火车轮轴车削工件车削工件杆件受垂直于

9、杆轴的横向力或通过杆轴平面内的外力偶作用，其杆件受垂直于杆轴的横向力或通过杆轴平面内的外力偶作用，其主要变形是主要变形是使杆的轴线弯曲成曲线。使杆的轴线弯曲成曲线。以弯曲为主要变形的杆称为梁。以弯曲为主要变形的杆称为梁。二、平面弯曲二、平面弯曲(梁的受力和变形特点的简化梁的受力和变形特点的简化)1.具有纵向对称面。具有纵向对称面。2.梁的外力，外力偶作用在梁的纵向对称面内。梁的外力，外力偶作用在梁的纵向对称面内。3.梁的中心线弯曲变形后在纵向对称面内成连梁的中心线弯曲变形后在纵向对称面内成连续光滑的挠曲线。续光滑的挠曲线。113. .简支梁简支梁1. .外伸梁外伸梁2. .悬臂梁悬臂梁三、三、

10、简单梁的基本形式简单梁的基本形式车削工件简化车削工件简化火车轮轴简化火车轮轴简化ABCFFAFBABFFAFBMqAFFAMqMA简单梁的支座一般可以简化为固定铰支座简单梁的支座一般可以简化为固定铰支座可动铰支座和固定端三种可动铰支座和固定端三种基本形式，基本形式，作用在其上的载荷作用在其上的载荷可以简化为集中载荷可以简化为集中载荷分布载荷和集中力偶三种。分布载荷和集中力偶三种。ABxCF2F1F3aFAyFQMFN12 0 xF0N F 0yF 0)(FCM)(1axFxFMAy剪力剪力FQ ，和横截面相切。，和横截面相切。弯矩弯矩M ，纵向对称面内的力偶。，纵向对称面内的力偶。四、四、梁的

11、内力梁的内力-剪力和弯矩剪力和弯矩梁的内力称为梁的内力称为剪力和弯矩剪力和弯矩。ABxCF2F1F3mm1FFFAyQBCF2F3FByFQM剪力对梁段内任意一点的矩为剪力对梁段内任意一点的矩为顺时针顺时针转向时转向时为正，为正，反之反之为负。为负。弯矩使得梁段呈弯矩使得梁段呈上凹为正，反之为负。上凹为正，反之为负。五、五、剪力和弯矩的符号剪力和弯矩的符号FQFQMM+MM上凹为正上凹为正上凸为负上凸为负MMFN或或右半段右半段左半段左半段左半段左半段右半段右半段13 求图示简支梁求图示简支梁E截面的内力。截面的内力。ABaC2Faa1.5aEMe=FaABaC2Faa1.5aEMe=FaFA

12、yFByFQEMEFAy2FAE 0AM0aFFaaFBy233FFBy35FFAy 0yF0352QFFFE 0EM23233522aFaFaFME3QFFE 0yF02FFFByAy0222335EMaFaF解：确定支反力解：确定支反力截面法截面法确定确定内力内力14ABq4lCM=2ql2F=2ql已知已知F = 2ql，M = 2ql 2，求简支梁跨中点截面，求简支梁跨中点截面C上的剪力和弯矩。上的剪力和弯矩。1.剪力等于截面一侧所有的外力的代数和。剪力等于截面一侧所有的外力的代数和。2.弯矩等于截面一侧所有的外力对截面上的点之矩的代数和。弯矩等于截面一侧所有的外力对截面上的点之矩的代

13、数和。解解:支座反力支座反力C截面上的剪力和弯矩。截面上的剪力和弯矩。 ql3F0l 2l 4ql 3FMl 4F0FMAAB=+= - ）（ql3F0ql4FFFFBBAy=+= - 022Q422 2 qllqlFMqlqlF FBCBCABq4lCM=2ql2F=2qlFAFBqBFBFQCCMC15六、剪力和弯矩方程，剪力弯矩图六、剪力和弯矩方程，剪力弯矩图剪力、弯矩图：剪力、弯矩图：表示剪力、弯矩沿轴线的变化规律的图形。表示剪力、弯矩沿轴线的变化规律的图形。 以横坐标以横坐标x表示横截面在梁轴线上的位置，则各横截面上剪力和弯矩都可表示为表示横截面在梁轴线上的位置，则各横截面上剪力和弯

14、矩都可表示为x的函数，的函数， FQ = FQ (x) ，M = M (x)。这。这称为梁的剪力方程和弯矩方程，它们一般是称为梁的剪力方程和弯矩方程，它们一般是x的分段函数，有集中力、集中力偶、分布力的点为函数分段点。的分段函数，有集中力、集中力偶、分布力的点为函数分段点。悬臂梁受均布载荷作用悬臂梁受均布载荷作用。试写出剪力和弯矩方程，并画出剪力图和弯矩图。试写出剪力和弯矩方程，并画出剪力图和弯矩图。qlqxFQMFQql(+)Mql2/2(+)解：任选一截面解：任选一截面x ，剪力和弯矩方程，剪力和弯矩方程 lxqxxF0Q lxqxxM02/2qlFmaxQ2/2maxqlM qllFFQ

15、Q00（由特殊点内力值，作剪力弯矩图）（由特殊点内力值，作剪力弯矩图） 8/2 002qllMM 2/2qllM最大剪力和弯矩分别为最大剪力和弯矩分别为16 图示简支梁图示简支梁C点受集中力作用。试写出剪力和弯矩方程，并画出剪力图和点受集中力作用。试写出剪力和弯矩方程，并画出剪力图和弯矩图。弯矩图。ABlCFabx1x2RAyRByFb/lFa/lFQ(+)(-)(+)Fab/lM解：约束反力解：约束反力剪力和弯矩方程剪力和弯矩方程AC： axlFbxF11Q0/ axlFbxxM1110/CB：lxalFaxF22Q/ lxalxlFaxM222/剪力、弯矩图剪力、弯矩图 lFabaM/0M

16、(l)M(0)l /FaF, l /FbFByAyABlCFab17简支梁简支梁C点受集中力偶作用。写出剪力和弯矩方程并画剪力图和弯矩图。点受集中力偶作用。写出剪力和弯矩方程并画剪力图和弯矩图。ABlCMabABlCMabx1x2RAyRByM/l(+)FQ(+)(-)Ma/lMb/lM解：约束反力解：约束反力剪力和弯矩方程剪力和弯矩方程AC： axlMxF11Q0/ axlMxxM1110/CB：bxlMxF22Q0/bxl/MxxM2220特殊点内力值，特殊点内力值，作作图图00）（）（lMM / /lMbCMlMaCM）（）（l /MF, l /MFByAy18简支梁受均布载荷作用简支梁

17、受均布载荷作用, ,写出剪力和弯矩方程，并画剪力图和弯矩图。写出剪力和弯矩方程，并画剪力图和弯矩图。ABqlABqlxFAyFByMql2/8(+)解：约束反力解：约束反力剪力和弯矩方程剪力和弯矩方程 lxqx/qlxFQ02 lxqxqlxxM02/2/2特殊点内力，作剪力弯矩图特殊点内力，作剪力弯矩图 8/2/ 002qllMlMM 2/2/0QQqllFqlF2/qlFFByAyFQql/2ql/219外伸梁受载如图，作剪力、弯矩图。外伸梁受载如图，作剪力、弯矩图。ABDqa4aaq（+） M 81qa2/32qa2FAyFByABDqa4aaq FQ9qa/47qa/4qa（+）（）q

18、aFqaFByAy43,49解：约束力解：约束力剪力图剪力图, ,弯矩图。弯矩图。 剪力和弯矩方程剪力和弯矩方程AB：BC21121qxxFMqxFFAyAyQxaqMqxF22Qa49x0qxFFAyQ122max32/81qaMqaMB20外伸梁受载如图，作剪力、弯矩图。外伸梁受载如图，作剪力、弯矩图。ABCF=6kN3m2mM=6kN/m3mDq=2kN/m5kNF13kNFBA,解：约束力解：约束力剪力图剪力图, ,弯矩图弯矩图 剪力和弯矩方程剪力和弯矩方程CA：AD：x211)2x(qFFFA2Q-=22352152xxqxxFMxFqxFB3BQ.5x0 x2FQ25325. 65

19、 . 2, 63, 00, 052）（）（）（）（，）（）（333221MMMM12M2MABCF=6kN3m2mM=6kN/m3mDq=2kN/mFAFBx6FxM6kN=FFQ-11=5）（，）（0F7x2112F3Q2QDB：7561266.255x230 x11x)2x(q21Fx)2x(FM22A2-+=21七、载荷集度七、载荷集度q(x)与剪力和弯矩间的关系与剪力和弯矩间的关系)(d)(dd)(dQ22xqxxFxxM（1）在梁的某一段内，若无分布载荷作用，即）在梁的某一段内，若无分布载荷作用，即q=0，在该段梁上，在该段梁上FQ=常数，常数，剪力图是平行于剪力图是平行于x轴的直线

20、。轴的直线。M(x)是是 x的线性函数，其弯矩图为一倾斜直线。的线性函数，其弯矩图为一倾斜直线。FQ0，弯矩图向右上斜，弯矩图向右上斜，FQ0，FQ(x)向右上斜，弯矩图为下凸的曲线；向右上斜，弯矩图为下凸的曲线；q0，FQ(x)向右下向右下斜，弯矩图为向上凸曲线。斜，弯矩图为向上凸曲线。 （3 3）在集中力作用处，剪力发生突变，突变值等于该集中力的大小。在集中力作用处，剪力发生突变，突变值等于该集中力的大小。 （4 4）在集中力偶作用处，弯矩发生突变，突变值等于该集中力偶的大小。在集中力偶作用处，弯矩发生突变，突变值等于该集中力偶的大小。 22 外伸梁及其所受载荷如图，试作梁的剪力图和弯矩图

21、外伸梁及其所受载荷如图，试作梁的剪力图和弯矩图。 ABF=6kNM=6kN.mq= 6kN/mCD2m2m4mFCFB解：支座反力解：支座反力 kNF,kNFBC1725剪力图剪力图突变点的弯矩数值。突变点的弯矩数值。AC 段：斜向右下的直线，段：斜向右下的直线，CB 段：剪力为零处为极值点。段：剪力为零处为极值点。D处有集处有集中力偶，弯矩图有向上的突变。中力偶，弯矩图有向上的突变。弯矩图弯矩图m.x Fx q F BQE83200 mkN 2M mkN 14M mkN 12MEDC08. 4，2.8317196FQ12142020.08MABF=6kNM=6kN.mq= 6kN/mCD2m

22、2m4m23解：支座反力解：支座反力 剪力图剪力图弯矩图弯矩图AC段段:斜向右上的直线；斜向右上的直线；DC段段:水平线；水平线；DB段段:二次曲线顶点以右部分；二次曲线顶点以右部分；BE段段:二次曲线顶点以左部分二次曲线顶点以左部分;D处有一集中力偶，处有一集中力偶，M使梁向下弯，使梁向下弯，弯矩图弯矩图有一向下的突变。有一向下的突变。作图所需点的弯矩值：作图所需点的弯矩值：+_+qlqlql_+ql2/2ql2qlF,qlFBA220022/qlM,MqlM,MBDCAABF=qlM=ql2qCD1m2mFAFB1mABF=qlM=ql2qCD1m2m1m外伸梁受载如图，作剪力、弯矩图。外

23、伸梁受载如图，作剪力、弯矩图。 24ABqaCDqaaaABqaCDqaaaFByFAyMAAqaFAyMAFDyBCDqFByFDy解解: :约束反力约束反力2/qaFDy2/qaFAy2/2qaMA取取DBC为研究对象为研究对象取整体为研究对象取整体为研究对象2/3qaFBy（+ +）（+ +）（- -）FQqa/2qa/2qa（- -）（- -）Mqa2/2qa2/2组合梁受载荷如图，作剪力、弯矩图。组合梁受载荷如图，作剪力、弯矩图。作业：作业：25(a), (c), (d)25试根据剪力图作出结构的支承（设支承在试根据剪力图作出结构的支承（设支承在AC截面）和载荷图（梁上无集中力偶作用

24、）截面）和载荷图（梁上无集中力偶作用） CFFAlllC45kNA2m1m+_FQ1530AC_+_FQF/3F/32F/3AC已知梁的弯矩图，试画出其剪力图，并在梁上加上所受的载荷（设支承在已知梁的弯矩图，试画出其剪力图，并在梁上加上所受的载荷（设支承在AB截面）截面） 。 MFl/2Fl/2+_MFlFl+_F_FF+_FFF_ABl/2l/2MC2FCDABl2FlllFMCDABl/3l/3l/3FFl/3MFl/326一、平面曲杆一、平面曲杆 轴线为连续、光滑平面曲线的构件称为轴线为连续、光滑平面曲线的构件称为平面曲杆平面曲杆。二、用截面法求曲杆内力二、用截面法求曲杆内力曲杆的内力（

25、由平衡方曲杆的内力（由平衡方程求得）程求得）: : 用通过曲线曲率中心的法截面用通过曲线曲率中心的法截面m-m截曲杆，取截面右截曲杆，取截面右侧（也可以取左侧）为研究对象，画出各内力：侧（也可以取左侧）为研究对象，画出各内力：轴力轴力 FN（ j j ）,沿截面处轴线的切线，拉为正；剪力沿截面处轴线的切线，拉为正；剪力FQ (j j )，和截，和截面相切，对曲杆内一点取矩，顺转为正；弯矩面相切，对曲杆内一点取矩，顺转为正；弯矩M（ j j ），在，在曲杆轴线平面内，使曲杆曲率增加曲杆轴线平面内，使曲杆曲率增加( (半径变小半径变小) )为正。为正。第五节第五节 复杂情况下的内力及内力图复杂情况

26、下的内力及内力图jmmFR jjsinFFN cosFFjj jjsinFRM三、平面刚架：三、平面刚架： 由几根直杆组成，而各杆在其联接处的夹角不能改变由几根直杆组成，而各杆在其联接处的夹角不能改变，这种联接点称为这种联接点称为刚节点刚节点。有刚节点的框架称为刚架。有刚节点的框架称为刚架。各直杆和外力均在同一平面内的刚架为平面刚架各直杆和外力均在同一平面内的刚架为平面刚架。平面刚。平面刚架的内力一般有轴力、剪力和弯矩，架的内力一般有轴力、剪力和弯矩，内力符号的规定同曲杆内力符号的规定同曲杆，只是将，只是将弯矩图画在受压弯矩图画在受压一侧一侧。 刚架的研究方法是视刚架为几根直杆的组合，从刚架的

27、一端开始，分段作出其内刚架的研究方法是视刚架为几根直杆的组合，从刚架的一端开始，分段作出其内力图。力图。FQ(j j)FN(j j)M(j j)j jmFm27 已知平面刚架上的均布载荷集度已知平面刚架上的均布载荷集度q,长度长度l，试：画出刚架的内力图。，试：画出刚架的内力图。qBCAllqBCAllql/2qlql/2x1x2解：约束力。解：约束力。各段的内力方程各段的内力方程竖杆竖杆AB：横杆横杆BC：lxqxqlxM2222202/2/lxqxxFQ2220lxqlxFN2202/ lxqlxxM11102/ lxqlxFQ1102/(+)ql/2FN:轴力图轴力图qlql/2(+)(-)FQ:剪力图剪力图ql2/2M :弯矩图弯矩图28四、复杂载荷（四、复杂载荷（组合变形组合变形）作用下杆件的内力和内力图）作用下杆件的内力和内力图 当杆件的受力较为复杂时，可先将外力向杆件的轴线简化，当杆件的受力较为复杂时，可先将外力向杆件的轴线简化，将力向沿轴线和垂直将力向沿轴线和垂直于轴线的方向分解于轴线的方向分解，再把构件上的外力划分成几组简单载荷，其中，再把构件上的外力划分成几组简单载荷，其中每一种载荷对应着每一种载荷对应着一种基本变形一种基本变形, ,分别作出各基本变形内力图分别作出各基本变形内力图。 皮带轮轴皮