立体几何证明方法汇总

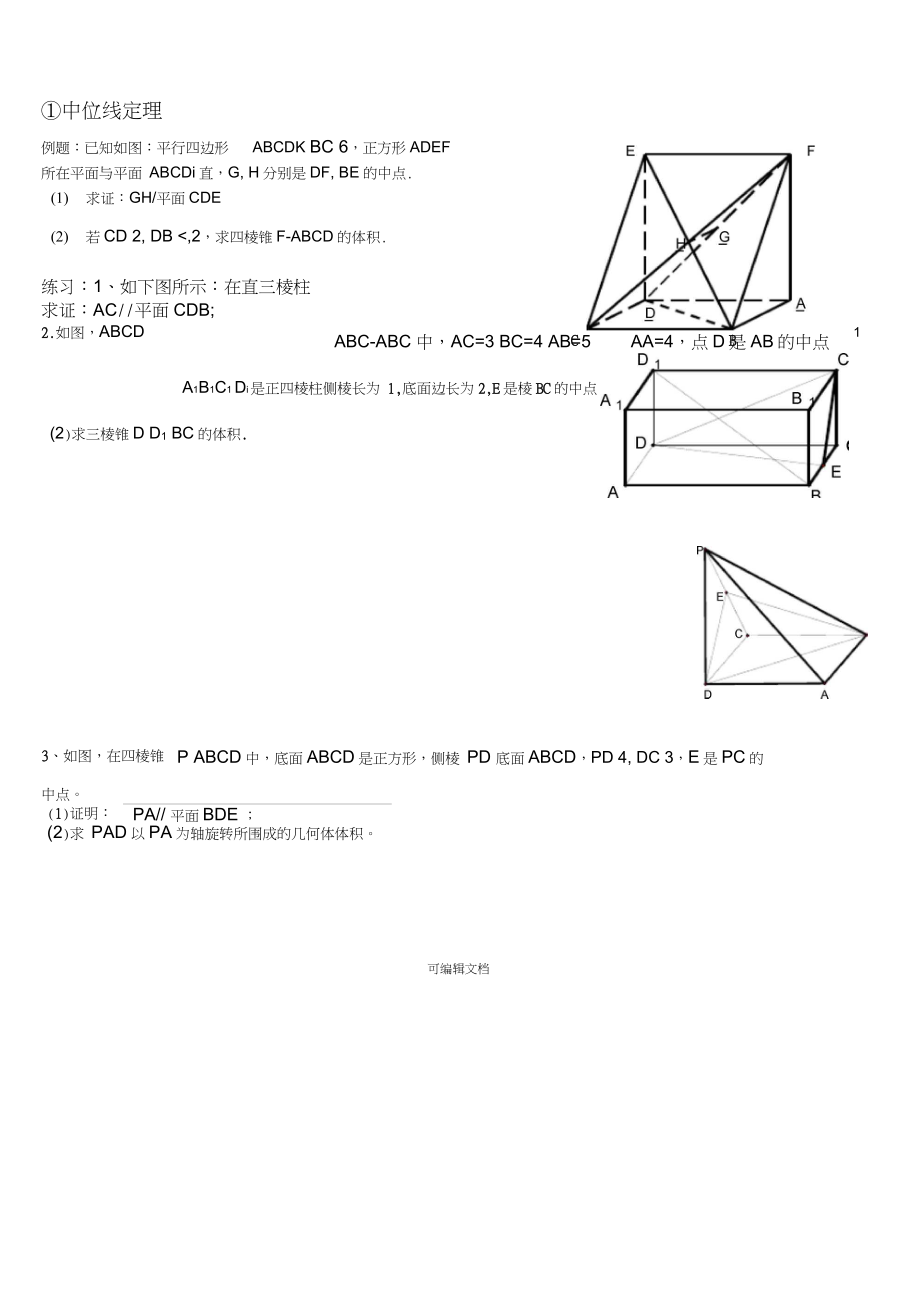
1、中位线定理例题：已知如图：平行四边形ABCDKBC 6，正方形ADEF所在平面与平面ABCDi直，G, H分别是DF, BE的中点.(1)求证：GH/平面CDE(2)若CD 2, DB ,2，求四棱锥F-ABCD的体积.求证：AC/平面 CDB;P ABCD中，底面ABCD是正方形，侧棱PD底面ABCD，PD 4, DC 3，E是PC的中点。(1 1)证明：PA/平面BDE；(2)求PAD以PA为轴旋转所围成的几何体体积。可编辑文档练习：1、如下图所示：在直三棱柱ABC-ABC 中，AC=3 BC=4 AB=5AA=4，点 D 是 AB 的中点2.2.如图，ABCDA1B1C1Di是正四棱柱侧

2、棱长为 1,1,底面边长为 2 2,E,E 是棱 BCBC 的中点。(1 1)求证：BDi平面CiDE；(2)求三棱锥D D1BC的体积. .3 3、如图，在四棱锥C CB B1例 2、如图，在矩形ABCD中，AB 2BC, ,P,Q分别为线段AB,CD的中点，EP丄平面ABCD. .求证：AQ/平面CEP；（利用平行四边形）如图，已知 P 是矩形 ABCD 所在平面外一点，PD 平面 ABCD, M N 分别是 AB PC 中点。求证:MN / 平面 PAD 如图，已知 ABAB 平面 ACDACD DE/ABDE/AB , ACDACD 是正三角形， AD=AD= DE=DE= 2AB2A

3、B 且 F F 是 CDCD 的中点. .求证：AF/AF/平面 BCEBCE练习：如图，PAPA 垂直于矩形 ABCDABCD 所在的平面,E E、F F 分别是 ABAB PDPD 的中点。求证： AF/AF/平面 PCEPCEPFGAEBC的交点.求证：Ci 面E EF FD DC C练习：1 1、如图所示，四棱锥P ABCD中，底面ABCD为正方形,PD平面ABCD,PD AB 2,E,F,G分别为PC、PD、BC的中点.(1 1)求证：；PA/ 面 EFG；面面平行-线面平行例题 4 4、如图，矩形 ABCDABCD 和梯形 BEFCBEFC 所在平面互相垂直， BE/CFBE/CF

4、 , 面 ABE/ABE/平面 CDFCDF(IIII )求证：AE/AE/平面 DCFDCF；(利用面面平行- -线面平行)比例关系例题 3 3、P P 是平行四边形 ABCDABCD 平面外一点,例关系) )M M N N 分别是 PBPB BCBC 上的点，且BM BN, ,求证：MN平面 PCDPCD 利用比PM NC练习：如图，四边形ABCD为正方形，EA平面ABCD,EF/AB,AB = 4,AE = 2, EF =1. .(n)若点M在线段AC1上，且满足CM -CA, ,求证：EM/平面FBC;4BCF=BCF=CEF=CEF=90可编辑文档4 4、(20122012 山东文)

5、如图，几何体E ABCD是四棱锥，ABD为正三角形， CBCB CD,ECCD,EC BDBD . .( (I) )求证：BE DE；( (n) )若/BCD 120,M为线段AE的中点,求证：DM/平面BEC. .(2)求三棱锥P EFG的体积.2 2、如图，在直三棱柱ABC AB1C1中，ACB 90,E，F，G分别是AA1,AC，BBl的中点，且CG ClG. .( (I) )求证：CG/平面BEF；3 3、如图所示, ,正方形ADEF与梯形ABCD所在的平面互相垂直, ,ADCD, AB/CD, CD2 AB 2 AD. .在EC上找一点M，使得BM /平面ADEF, ,请确定M点的位

6、置，并给出证明.BiGC CB B可编辑文档例题：如图，已知四棱锥P ABCD。若底面ABCD为平行四边形，E为PC的中点，在DE上取点F,过AP和点F的平面与 平面BDE的交线为FG，求证：AP/FG。练习：1 1、如图，在四棱锥P ABCD中，侧面PAD是正三角形，且与底面ABCD垂直，底面ABCD是边长为 2 2 的菱形,BAD 60，N是PB中点，过A N D三点的平面交PC于 M M .求证：AD/MN;2 2、（20122012 浙江高考）如图，在侧棱锥垂直底面的四棱锥ABCD-AQD 中，AD/ BCAD 丄 ABAB=2 AD=2,AD=2, BC=4,AA=2BC=4,AA=

7、2,E E 是 DDDD 的中点，F F 是平面 BCEBCE 与直线AA的交点。（1 1）证明：EF/EF/ AiDAiD;证明：连 AC 与 BD,设交点为 0,连 0EC C可编辑文档(K2ogEB)可编辑文档3.3.如图，四边形 ABCDABCD 是矩形，平面 ABCDABCD 平面 BCEBCE BEBE EC.EC.(1)求证：平面 AECAEC 平面 ABEABE ( (面面垂直性质) )BF1(2)点 F F 在 BEBE 上，若 DE/DE/平面 ACFACF 求 的值。(线面平行的性质 )BE2例、如图，在正方体ABCD AB1C1D1中，E、F、G分别是AB、AD、CiD

8、i的中点. . 求证：平面D1EF/平面BDG. .练习：如图所示，在正方体 ABCD-ABCD-A1B1C1D1中，E E、F F、G G H H 分别是 BCBC CCCC、CQCQ、AAAA 的中点. .求证:(1) EG/平面 BBDD; (2)平面 BDF/ 平面 BiDH.例题：已知在正方体 ABCD-ABCD-AiB1C1D1中，E,FE,F 分别是C1D1和D1A1上的点，点 P P 在正方体外，平面 PEFPEF 与正方体相交于 AC,AC,求证：EF /平面 ABCD可编辑文档菱形的对角线互相垂直：例题。已知 E E, F F 分别是正方形 ABCDABCD 边 AD,AD

9、, ABAB 的中点，EFEF 交 ACAC 于 M M GCGC 垂直于 ABCDABCD 所在平面。 求证：EFEF 丄平面 GMCGMC练习：如图ABCDABCD- -AiBiCiDi是底面为正方形的长方体，求证：（1 1） BDBD 平面ACCiA等腰三角形底边的中线垂直底边例 1、如图，在三棱锥P ABC中，AC BC 2,AP BP AB,PC AC求证：PC AB；P PA AD DB BC C（2）BD AC1ACB90,P P可编辑文档练习：1、在三棱锥 A-BCD 中，AB=AC,BD=D（求证：BC AD圆的直径所对的圆周角为直角例题 3 3、如图 ABAB 是圆 0 0

10、 的直径，C C 是圆周上异于 A A、B B 的任意一点，PA平面 ABCABC（ 1 1）图中共有多少个直角三角形？（ 2 2）若AH PC, ,且 AHAH 与 PCPC 交于 H,H,求证：AHAH 平面 PBC.PBC.利用勾股定理例 4 4、在长方体ABCD中，底面ABCD是边长为 1 1 的正方形，侧棱B BAA!2，E E 是侧棱BB1的中点。求证：AE平面AD；证明：ABCDA.BQ.D,为长方体，练习：如图，四棱锥 P-ABCD 的底面是边长为 1的正方形，D1C1PA CD, PA 1, PD .2,求证：（1）PA 平面 ABCD（2） 求四棱锥 P-ABCD 的体积.

11、AB可编辑文档间接法，用线面垂直的性质定理（丨b,b lb）例题：如图，四棱锥 P-ABCDP-ABCD 中，底面 ABCDABCD 为平行四边形，DAB 60,AB 2AD, PD 底面 ABCD，证明：PA BD; ;练习 1如图，在直三棱柱ABC A1B1C1中，AC=3 3,BG4, AB=5 5,AA14,点D是AB的中点。（i）求证：AC BC1；练习 2 2:如图，四边形ABCD为矩形，BC平面ABE,F为CE上的 点，且BF平面ACE. .求证：AE BE;证明：因为BC平面 ABE,AE平面 ABE,例 1 1 如图，AB是OO的直径,PA垂直O 0所在的平面,C是圆上不同于

12、A,B的任意一点，求证：平面PACL平面PBCP PC0 0可编辑文档练习 1 1：如图，棱柱ABC A1B1C1的侧面BCC1B1是菱形，A1B可编辑文档2、如图，在直三棱柱ABC A1B1C1中，E、F 分别是A1B、A1C的中点，点 D 在BQ上，A1D B1C求证：(1)EF/平面 ABC (2)平面AFD平面BB1C1C.3 3、如图，ABCD是正方形，S S 从平面ABCDBKBKSCSC 于 K K，连结 求证(1 1)平面SBCL平面KBDPABCD，侧面PADL底面ABCD侧棱PA= PD O为AD中点，求证：PCL平面ABCD例 2 2:如图，在四棱锥P ABCD中，底面A

13、BCD是DAB平面PAD垂直于底面ABCD(1) 若G为AD的中点，求证：BG平面PAD；(2) 求证：AD PB;练习：1 1、如图 ABAB 是圆 0 0 的直径，C C 是圆周上异于AB B 的任意一点，PA平面 ABCABC (1 1)图中共有多少个直角三角 形？ ( 2 2)若AH PC, ,且 AHAH 与 PCPC 交于 H,H,求证：平面 PACPAC 平面 PBC.(3)PBC.(3) AHAHDKDK例 1 1 :如图，在四棱锥600且边长为a的菱形，侧面PAD是等边三角形，且平面 PBCPBCD DC CH H0 0可编辑文档2 2、在四棱锥P ABCD中，平面 PAD!

14、PAD!平面 ABCDABCD AB=ADAB=AD / BAD=60BAD=60 , E E、F F 分别是 APAP ADAD 的中点. . 求证：平面 BEFBEF!平面 PADPAD3 3、如图，正方形 ABCDABCD 所在平面与以 ABAB 为直径的半圆 0 0 所在平面 ABEFABEF 互相垂直, 点，求证：。1直线 AP!AP!平面 PBCPBC 平面 PBCLPBCL 平面 APCAPC4 4、如图，三角形 ABC 中, AC=BC 二AB, ABED 是边2丄底面 ABC 且，若 G F 分别是 EC BD 的中点，（I）求证：GF/底面 ABC5 5、如图，A B, C

15、，D 为空间四点在 ABC 中，（U）求几何体 ADEBC 勺体积 V。长为a的正B BP P 为半圆周上异于 A A，B B 两点的任可编辑文档AB 2, AC BC2.等边三角形 ADB 以 AB 为轴运动.（I）当平面 ADB 平面 ABC 时，求 CD ;可编辑文档的中点.(1)求证：0D/平面 PAC (2)求证：平面 PAB 丄平面 ABC ;(3)求三棱锥 A PBC 的体积.2 2、如图,长方体ABCD A1B1C1D1中，AB AA11, ,AD 2, ,E是BC的中点(I)(I)求证：平面A,AE平面D1DE; (II)(II)求三棱锥A A1DE的体积. .五、体积问题1

16、.如图，ABCD A.B.C.D,是正四棱柱侧棱长为(1) 求证：BDi/平面CiDE;(2) 求三棱锥D DiBC的体积.1,底面边长为 2，E 是棱 BC 的中点练习 1 1：三棱锥 P ABC 中,PAC 和 PBC 都是边长为 2 的等边三角形，AB2,0、D 分别是 AB PBA A1D D1可编辑文档几何体的棱AG上的中点。（I）求出该几何体的体积；（3 3）（n）求证：直线BC,/ /平面 AB,D:（川）求证：3、如图，在四棱锥 P-ABCD 中，PD 垂直于底面 ABCD，底面 ABCD 是直角梯形，DC / AB, BAD 90,且AB 2AD 2DC 2PD 4 （单位：

17、cm），E为PA的中点。（1）如图，若主视方向与AD平行，请作出该几何体的左视图并求出左视图面积:（2）证明：DE/平面 PBC；P4 4、已知某几何体的直观图（图 1 1）与它的三视图（图 2 2），其中俯视图为正三角形，其它两个视图是矩形. .已知D是这个A AiA AC CiB BiB B百I可编辑文档5 5、已知某个几何体的三视图如图（主视图的弧线是半圆）（I）求这个组合体的体积；（H）若组合体的底部几何体记为ABCD A1B1C1D1，其中A1B1BA为正方形（ i i ）求证：AiB 平面 ABiCiD； （iiii ）求证：P为棱AiBi上一点，求AP PCi的最小值. .，根据

18、图中标出的数据,可编辑文档六:等体积法求高（距离）：h如：三棱锥 VFBECI= VBEFCiis sBECih= =is sEFCiBEBE33例题（20i020i0 广东文数）如图，弧 AECAEC 是半径为a的半圆，ACAC 为直径，点 E E 为弧 ACAC 的中点，点 B B 和点 C C 为线段 ADAD 的三等分点，平面 AECAEC 外一点 F F 满足 FCFC 平面 BED,FBBED,FB5a（i i）证明：EBEB FDFD （2 2）求点 B B 到平面 FEDFED 的距离AD可编辑文档练习 1 1:已知 ABC-AABC-A1B B1C C1是正三棱柱，棱长均为5

19、, E E、F F 分别是 ACAC A A1C C1的中点,(1(1)求证：平面 ABFABF /平面 BECBEC(2(2)求点 A A 到平面 BECBEC,间的距离点D到平面PBC的距离.AE AFADB 6oO，E，F分别是AC，AD上的动点且7C=AF=，(0 1)(1)求证：不论 为何值，总有EF 平面 ABC;1(2)若=,求三棱锥A-BEF的体积.2ABCD是菱形,作与PD平行的平面交PB与点E,ABCD的两对角线交点为F.(I)求证:边长为ACDE;BCD 60(n)若EF经过AC.3，求3 3、如图 4 4,在四棱锥P ABCD中，平面PAD平面ABCD,AB /DC PAD是等边三角形，已知BD 2AD 4,AB2 DC2.5.(1 1)求证：BD平面PAD;(2 2)求三棱锥A PCD