线性体系随机振动反应分析

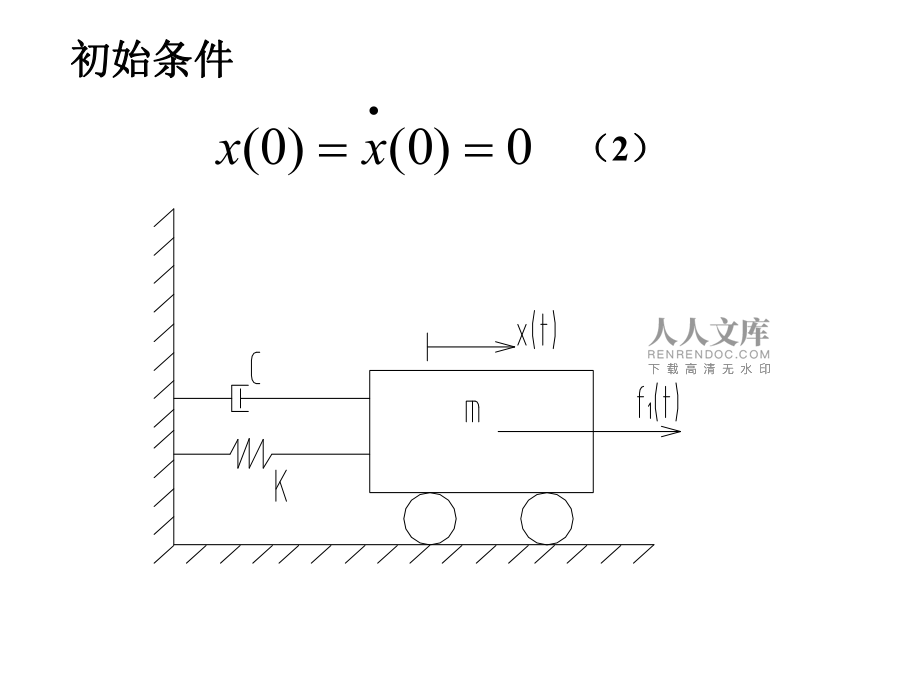
1、线性体系随机振动反应分析线性体系随机振动反应分析 研究线性体系在平稳或非平稳随机干扰下的反应，初研究线性体系在平稳或非平稳随机干扰下的反应，初始条件可以确定的，也可以是随机的。始条件可以确定的，也可以是随机的。1、单自由度线性体系的随机反应分析、单自由度线性体系的随机反应分析基本方程：基本方程： (1)式中式中 是描述质点运动的位移是描述质点运动的位移； )(2200tfxxx mkc2mk0mtftf/ )()(1ckm,分别为结构体系的阻尼比和固有圆频率分别为结构体系的阻尼比和固有圆频率； )(tx和和；为体系的质量，弹簧刚度和粘滞阻尼系数。为体系的质量，弹簧刚度和粘滞阻尼系数。 初始条件

2、初始条件 0)0()0(xx （2）1）时域分析）时域分析 Duhamel积分法：将整个荷载时程看作是由积分法：将整个荷载时程看作是由一体系连续的短持续时间脉冲组成。先求短一体系连续的短持续时间脉冲组成。先求短脉冲作用下的反应，然后用叠加原理求得总脉冲作用下的反应，然后用叠加原理求得总反应反应 微冲量微冲量 dssf)(s设设 时刻的单位脉冲时刻的单位脉冲 的反应的反应 则则 在微冲量作用下的反应为在微冲量作用下的反应为 )(st )(sthdssfsthtdx)()()( （3） 总反应为总反应为tdssfsthtx0)()()(（4） 也称为脉响函数。也称为脉响函数。 时时 （脉冲发生前无

3、响应）（脉冲发生前无响应）考虑考虑 的情况，故当的情况，故当 时，时，)(2200thhh1)2(20000dthhh)(sthst 0)( sth0s)()(ttf（5） （6）两端作跨零积分，有两端作跨零积分，有1)2(20000dthhh（7） 利用（利用（6），得），得00200000000000000000)(022)(2)0(dtthhdhthhhhddth故故 （8）作用一个单位脉冲，产生初速度）作用一个单位脉冲，产生初速度1)0(h相当于相当于 ）（及）齐次化（101)0(, 0)0(902200hhhhh的解的解 从而从而 )11(000sin)exp(1)(0ttttthd

4、d201d式中式中 2）频域分析法）频域分析法tiefxxx0202（12） 初始条件：初始条件： 0)0()0(xx设设 tiAetx)(则则 titiefAeii020022)(（14） 故故 tiefHtx0)()(（15） 式中式中 022021)(iH（16） 称为体系的频响函数或传递函数，它表称为体系的频响函数或传递函数，它表示在干扰示在干扰 下反应下反应 的振幅放大率，是线性体系的振幅放大率，是线性体系的固有频率特性。的固有频率特性。 对任意函数对任意函数 ，可用，可用Fourier变换表示成变换表示成)(H)(tf)(tx)(tfdtetffti)(21)(（17） dteft

5、fti)()(（18） 逆变换逆变换 即即 在任意荷载作用下，在任意荷载作用下，dtefHtxti)()()(（19）3）脉动函数和频响函数的关系）脉动函数和频响函数的关系 设设 是单位脉冲时，它的是单位脉冲时，它的Fourier变换变换由式（由式（17），可求得为），可求得为)()(ttf21)(21)(dtetfti（20） 代入式（代入式（19），则得单位脉冲作用下得反应函数为），则得单位脉冲作用下得反应函数为 deHthti)(21)(（21） 即：即： 除除 处，脉响函数处，脉响函数 和频响函数和频响函数 是是Fourier变换时变换时 21)(th)(HdtethHti)()(（2

6、2） 2平稳随机干扰下的反应平稳随机干扰下的反应 )(2200tFXXXs（23） FX,0)0()0(XX大写字母大写字母 为随机变量为随机变量 （24） 初始条件初始条件： 反应谱 单自由度弹性体系的地震反应 反应谱的定义 反应谱的性质 反应谱的影响因素及规律单自由度弹性体系的地震反应 单自由度弹性体系mk cxg(t)xg(t)m(x+xg)cxkx 运动微分方程 受力分析 恢复力虎克定律 阻尼力瑞雷阻尼 惯性力牛顿第二定律 方程建立达朗贝尔原理 运动微分方程的解答gxxxx 220)(kxxcxxmg 运动微分方程的解答 通解（自由振动） 特解（强迫振动）Duhamel 积分 全解=通

7、解+特解 特解 位移txxtxetxdddtsin)0()0(cos)0()(dtextxdttgd)(sin)(1)()(0 txxtxetxdddtsin)0()0(cos)0()(dtexdttgd)(sin)(1)(0 21d运动微分方程的解答 设初始位移和初始速度为零，则有 速度 绝对加速度 dtextxdtgtd)(sin)(1)()(0 dttextxdddtgt)(sin)(cos)()()(0 dtextxtxddtgtdg)(sin)1 ()()()(222)(0 dtexdtgt)(cos)(2)(0 运动微分方程的解答 最大反应及简化三点近似关系： max)(txSdm

8、ax)(txSVmax)()(txtxSga dVaSSS2反应谱的定义 单自由度弹性体系在给定地震作用下某种反应量的最大值与体系自振周期之间的关系曲线Sa(, T1)Sv(, T1)Sd(, T1)xg(t)Duhamel 积分s(t)= f(xg, , T1)MaxT1TiSa(, Ti)Sv(, Ti)Sd(, Ti)Duhamel 积分s(t)= f(xg, , Ti)MaxTSyT1Ti 问题反应谱到底反映了结构的特性还是地震动的特性？反应谱的性质 结构反应特点 低频（长周期）系统（=10Hz） SaPGA （有效峰值加速度） 反应谱性质 反应谱由中频段的放大区和两端的极限区三部分构

9、成 伪谱的性质T高频中频低频动力放大系数Ba=Sa/PGABv=Sv/PGV Bd=Sd/PGDdVaSSS2反应谱的影响因素及规律 地震动方面 震级 震级越大，长周期成分越丰富，反应谱峰点周期越后移 震中距 震级越大，长周期成分越丰富，反应谱峰点周期越后移 场地 场地越软，峰值越大，反应谱峰点周期越后移 结构方面 阻尼比 阻尼比越大，反应越小，曲线越平滑 结构周期 三段特性持时特性 一般特征 多种定义 简要评价-2.5-1.5-0.50.51.52.50510152025303540t (s)a(t) (m/s2)设计地震动反应谱（2010规范） 水平地震影响系数back 水平地震影响系数曲

10、线GkGgPGAPGASgmmSFaaT(s)max0.45max0 0.1Tg 5 Tg6.0max2)(TTgmax12)5(2 . 0gTT1.建筑阻尼比取0.05；2.建筑阻尼比不等于0.05时；衰减指数直线下降段斜率调整系数 小于0时取0 3.阻尼调整系数 当小于0.55时取0.55这里 为阻尼比63 . 005. 09 . 032405. 002. 016 . 108. 005. 012设计地震动反应谱back1、水平地震影响系数最大值烈度6789多遇地震1836（55）72（110）140罕遇地震125220（310）400（510）620烈度6789多遇地震0.040.08（0.12）0.16（0.24）0.32罕遇地震0.280.50（0.72）0.90（1.20）1.40注：括号内数值分别用于设计基本加速度为0.15g和0.30g的地区注：括号内数值分别用于设计基本加速度为0.15g和0.30g的地区2、时程分析用的地震