


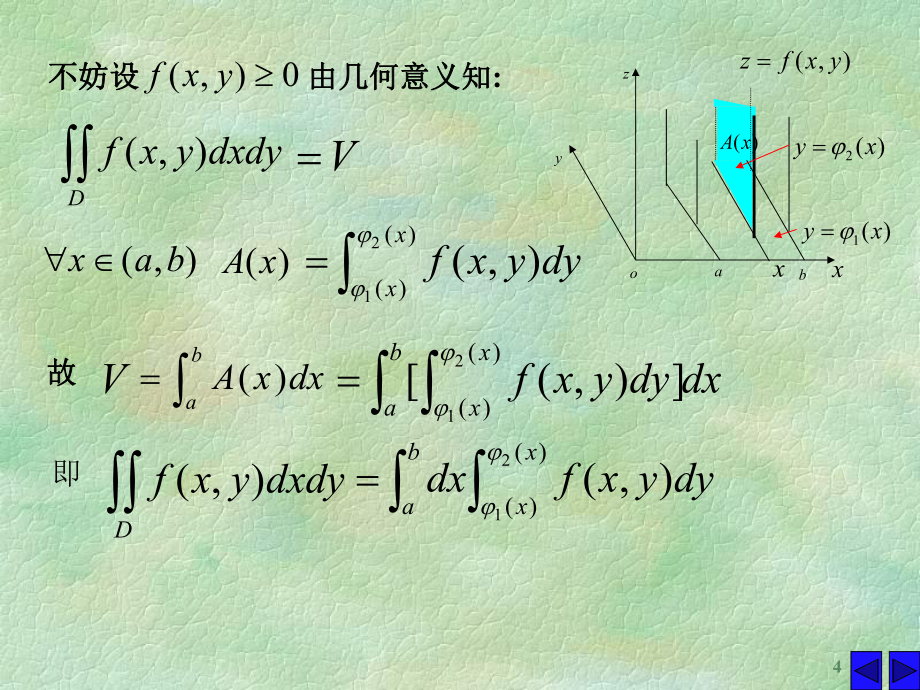

版权说明:本文档由用户提供并上传,收益归属内容提供方,若内容存在侵权,请进行举报或认领
文档简介
1、16.8 6.8 二重积分的计算二重积分的计算:把:把二重积分二重积分化为化为两次定积分两次定积分来计算来计算2Ddyxf),(Ddxdyyxf),(dxdydiiniidyxf),(lim10yxikjyx 面积元素面积元素Ddyxf),(i6.8.1 在直角坐标系下二重积分的计算在直角坐标系下二重积分的计算3)()(,),(:21xyxbxayxDDdxdyyxf),(dx先先y后后x的两次积分的两次积分.记作记作:Ddxdyyxf),(baxxdyyxfdx)()(21),(1.积分区域积分区域D为为:X型区域型区域xyoab)(1xy)(2xyx abdyyxf),()(1x)(2x4
2、x)(xA不妨设不妨设0),(yxf由几何意义知由几何意义知:V),(bax)(xA故故VbadxxA)(dxdyyxfbaxx )()(21),(即Ddxdyyxf),(baxxdyyxfdx)()(21),(Ddxdyyxf),(yxzoab),(yxfz )(1xy)(2xy)()(21),(xxdyyxf5)()(,),(:21yxydycyxD2.积分区域积分区域D为为Y型区域型区域dcyydxyxfdy)()(21),(先先y后后x的两次积分的两次积分.Ddxdyyxf),(xyocd)(2yx)(1yxyDdxdyyxf),(dycddxyxf),()(1y)(2y6dcbadx
3、yxfdy),(Ddxdyyxf),(说明说明badcdyyxfdx),(3).如果平行于坐标轴的直线与积分区域如果平行于坐标轴的直线与积分区域D的的边界交点多于两点边界交点多于两点, 则作辅助线把则作辅助线把D分为若干分为若干X-区域区域或或Y-型区域型区域.Ddxdyyxf),(badxxf)(1dcdyyf)(2dycbxayxD,),(:1).积分区域积分区域D为为 矩形矩形2).若被积函数若被积函数 f (x,y) = f1(x) f2(y) ,dycbxayxD,),(: 积分区域积分区域D为为 矩形矩形7步步 骤:骤:(2)写出区域)写出区域D上的点的坐标满足的不等式,上的点的坐
4、标满足的不等式, 从而定出积分的上下限从而定出积分的上下限.2.在在 x 轴上轴上 a , b 内任取一点内任取一点 x ,做做 x 轴的垂线,垂线落在轴的垂线,垂线落在 D 内的线段,内的线段,y 从从 1(x) 到到 2(x)说明说明二重积分化为两次积分时,二重积分化为两次积分时,确定积分限确定积分限是关键是关键.(1)画出区域)画出区域D的图形的图形1. x 从从 a 到到 b,例:若例:若D为为X-区域区域Ddxdyyxf),(baxxdyyxfdx)()(21),()()(,),(:21xyxbxayxDxyoab)(1xy)(2xyx 8例例1. 化二重积分化二重积分Ddxdyyx
5、f),(为两次积分为两次积分.xyxxyD1, 2,:解解:画草图画草图,xyxxyxD1,21),(:或或21DDD21, 121),(:1xyyyxD2, 21),(:2xyyyxD21/ 1),(xxdyyxfdx2/112/1),(ydxyxfdy221),(ydxyxfdyDdyxf),(xyo12D1D2D12219yydxyxfdyI2202),(xyo42yx22yx DyxyyyxD2,20),(:2xxdyyxfdx2/40),(解解:xyxxyxD2,40),(:或或I例例2. 交换积分次序交换积分次序10解解21DDDyxyyxD20, 10),(:1yxyyxD30,
6、 31),(:2xyo1231D2Dyx 3yx2xyxxyxD32,20),(:2032/),(xxdyyxfdx1020),(ydxyxfdyI+ydxyxfdy3031),(例例3. 交换积分次序交换积分次序I11例例4. 计算计算Dxydxdy其中其中D是由直线是由直线xyxy, 2, 1所围所围.解解: 画草图画草图,Dxydxdyxxydydx121dx21212) 1(21dxxx89另解另解:2,21),(:xyyyxDDxydxdy221yxydxdy21dyxyxyxD1 , 21),(:212)4(21dyyyxyo112xyD2891212xxy2221yxy12xyo
7、241) 1, 1 ( )2 , 4(D2例例5. 计算计算Dxydxdy其中其中D由由2,2xyxy所围所围.解解:画草图画草图2, 21),(:2yxyyyxDDxyd2212yyxdxydydyxyyy2122221dyyyy)2(2142128551D2DDxyd1Dxyd2Dxyd另解:另解:xxydyxdx10 xxydyxdx24185513dxdyxxDsin解解:画草图画草图,xyxxyxD2, 10),(:xxdyxxdx2sin10dxxxxx)(sin21010)sin(sindxxxx1sin1xyxyD,:2所围所围.例例6. 计算计算dxdyxxDsin注意注意选
8、择积分次序的原则:选择积分次序的原则:1.积分区域积分区域, 尽量避免分块尽量避免分块;2.被积函数被积函数, 第一次积分易积第一次积分易积.1xyo1dxdyxxDsin或或:yydxxxdysin10不能计算不能计算14例例7. 用二重积分计算由用二重积分计算由2,2xyxy所围成的图形的面积所围成的图形的面积.解解: 画草图画草图,2, 21),(:2xyxxyxDDdxdy2212xxdydx212)2(dxxx29 xyo1 22xyD2xyA面面积积或或212)2(dxxx29 A面面积积15例例8. 求两个底圆半径等于求两个底圆半径等于R 的直交圆柱所围成的立体的体积的直交圆柱所
9、围成的立体的体积.解解. 建立坐标系如图建立坐标系如图,两圆柱面的方程为两圆柱面的方程为:,222Ryx.222Rzx由对称性知由对称性知,所求体积为第一卦限部分的所求体积为第一卦限部分的8倍倍.1VDzdxdyDdxdyxR22dyxRdxxRR220220RdxxR022)(332R所求体积所求体积18VV 3316RyxRR22xRy xyzoRRDor M),(r在极坐标系中在极坐标系中M点的极坐标点的极坐标),(rM极极径径 r极极角角 常常数数 r代表以极点为圆心的圆代表以极点为圆心的圆常常数数 代表从极点出发的一条射线代表从极点出发的一条射线)00( ,极点极坐标系极坐标系2、在
10、极坐标系下二重积分的计算、在极坐标系下二重积分的计算在直角坐标系中在直角坐标系中 rdrddxdy cosrx sinry Drdrdrrf)sin,cos(dxdyyxfD),(xoryyx M),(yx),(r),(yxM在极坐标系中在极坐标系中),(rM22yxr xytan 1.极点在区域之外极点在区域之外.)()(,),(:21rrrrDdxdyyxfD),(rdrrrfd)sin,cos(oDA)(2rr)(1rrDrdrdrrf)sin,cos(dxdyyxfD),(Drdrdrrf)sin,cos()(2r)(1r2. 极点在区域的边界上极点在区域的边界上.)(0 ,),(:r
11、rrDDdxdyyxf),()(0)sin,cos(rrdrrrfd3. 极点在区域之内极点在区域之内.)(0 ,20),(:rrrDDdxdyyxf),()(020)sin,cos(rrdrrrfdDAo)(rr AoD)(rr 一般一般,积分区域为圆形、扇形或环形时,积分区域为圆形、扇形或环形时,)(),(),(22xyfyxfyxf或者被积函数为或者被积函数为 利用极坐标计算比较简单利用极坐标计算比较简单.解解. 画草图画草图例例1. 计算计算, 422yx所围第一象限部分所围第一象限部分., D由圆周由圆周122 yx及直线及直线0,yxy21 ,40),(:rrDDdxdyyx)(2
12、221340drrdd4016151212oxyxy DDrdrdr241214rDdxdyyx)(22, 例例2. 计算计算Dyxdxdye221:22 yxD解解: 画草图画草图.10 ,20),(:rrDDyxdxdye2210202rdredrder20102)21()1 (1ede201)2121(Drrdrde2xyD122解解: 画草图画草图.cos20 ,22),(:rrDDdxdyyx22cos20222drrd例例3. 计算计算Ddxdyyx22xyxD2:22,xyD2o223cos38d203cos316d.932xyx222cos22rr cos2rDrdrdr解解. 画草图画草图例例4.计算计算Ddxdyxyarctan, 922 yx所围第一象限部分所围第一象限部分.,D由圆周由圆周122 yx及直线及直线0,yxy31 ,40),(:rrDDdxdyxyarctan3140rdrdDrdrd404d82D1313oxyxy 例例5. 求球体求球体22224azyx被圆柱面被圆柱面)
温馨提示
- 1. 本站所有资源如无特殊说明,都需要本地电脑安装OFFICE2007和PDF阅读器。图纸软件为CAD,CAXA,PROE,UG,SolidWorks等.压缩文件请下载最新的WinRAR软件解压。
- 2. 本站的文档不包含任何第三方提供的附件图纸等,如果需要附件,请联系上传者。文件的所有权益归上传用户所有。
- 3. 本站RAR压缩包中若带图纸,网页内容里面会有图纸预览,若没有图纸预览就没有图纸。
- 4. 未经权益所有人同意不得将文件中的内容挪作商业或盈利用途。
- 5. 人人文库网仅提供信息存储空间,仅对用户上传内容的表现方式做保护处理,对用户上传分享的文档内容本身不做任何修改或编辑,并不能对任何下载内容负责。
- 6. 下载文件中如有侵权或不适当内容,请与我们联系,我们立即纠正。
- 7. 本站不保证下载资源的准确性、安全性和完整性, 同时也不承担用户因使用这些下载资源对自己和他人造成任何形式的伤害或损失。
最新文档
- GB 14930.2-2025食品安全国家标准消毒剂
- 湖北工程职业学院《土木工程施工技术与组织课程设计》2023-2024学年第二学期期末试卷
- 山东轻工职业学院《电影摄影技巧》2023-2024学年第二学期期末试卷
- 乌兰察布职业学院《数理统计理论与方法国际2》2023-2024学年第二学期期末试卷
- 食堂食品原材料采购合同书
- 中对照装饰施工合同
- 尾矿库工程承包合同
- 客厅吊灯灯具买卖合同
- 衣柜购销合同
- 并购居间服务合同
- 南开一模试题及答案物理
- 茶叶生产关键影响因素与高产栽培技术研究
- 施工质量奖惩考核实施细则
- 人教版五年级音乐下册(简谱)第二单元《阿喽喽》教学设计
- 2025年入团考试练习试题(100题)附答案
- JGJ/T235-2011建筑外墙防水工程技术规程
- (正式版)HG∕T 21633-2024 玻璃钢管和管件选用规定
- 浙江省宁波市鄞州区2023 学年第二学期八年级科学期中考试试卷
- 中华民族共同体概论课件专家版2第二讲 树立正确的中华民族历史观
- 国家开放大学《人文英语3》章节测试参考答案
- 幼儿绘本故事之十二生肖

评论
0/150
提交评论