函数的单调性 (中职)（课堂PPT）

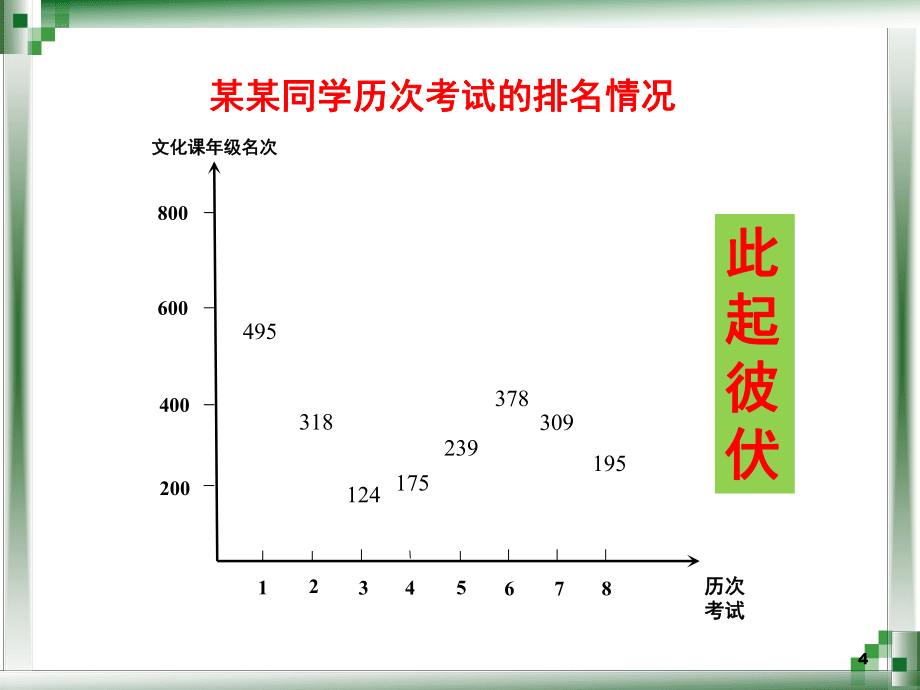
1、1授课教师：潘健林授课教师：潘健林富阳区职业高级中学数学组富阳区职业高级中学数学组22012201320142015201620172018300600900120015001800销售额（亿）销售额（亿）年份年份2100历年来双历年来双“11”天猫天猫 淘宝成交额变化图淘宝成交额变化图蒸蒸蒸蒸日日上上191350571912120716822135320132014201520162017200400600800销售额（亿）销售额（亿）年份年份娃娃哈哈集团近年销售额变化图哈哈集团近年销售额变化图每每况况愈愈下下783728677575529412345200400600800文化课年级名次文

2、化课年级名次历次历次考试考试某某同学历次考试的排名情况某某同学历次考试的排名情况此此起起彼彼伏伏4953181241752396783783091955画出函数y=x+1、y=-x+1、y=x2图像，并且观察函数的图像当自变量从左到右变化时，图像有什么样的变化规律.6xyy=x+1O11第一个函数图像第一个函数图像从左至右图象从左至右图象呈呈_趋势趋势. .上升上升7xyy=x+1O11第一个函数图像第一个函数图像从左至右图象从左至右图象呈呈_趋势趋势. .上升上升y=-x+1xyO11第二个函数图像第二个函数图像从左至右图象从左至右图象呈呈_趋势趋势. .下降下降8xyy=x+1O11第一个

3、函数图像第一个函数图像从左至右图象从左至右图象呈呈_趋势趋势. .上升上升y=-x+1xyO11第二个函数图像第二个函数图像从左至右图象从左至右图象呈呈_趋势趋势. .下降下降第三个函数图像第三个函数图像xyy=x2O11从左至右图象从左至右图象呈呈_趋势趋势. .局部下降或上升局部下降或上升910 xyy=x2O11图像从左到右逐渐上升图像从左到右逐渐上升图像从左到右逐渐下降图像从左到右逐渐下降自变量自变量x增大增大,自变量自变量x增大增大,在定义域内的某个区间上在定义域内的某个区间上因变量因变量y也增大也增大因变量因变量y反而减小反而减小11 函数单调性定义函数单调性定义 函数函数 ，定义

4、域为，定义域为A，区间，区间 ( )yf xIA 如果在区间如果在区间I I内内随着自变量随着自变量 的增大，因变量的增大，因变量 也也增大增大 ，那么我们称函数在区间，那么我们称函数在区间I I上是上是增函数增函数 xy 如果在区间如果在区间I I内内随着自变量随着自变量 的增大，因变量的增大，因变量 减小减小 ，那么我们称函数在区间，那么我们称函数在区间I I上是上是减函数减函数 xy12对区间对区间I内内 x1，x2 ，当当x1x2时，时， 有有f(x1)f(x2)xx1x2都都yf(x1)f(x2)O设函数设函数y=f(x)的定义域为的定义域为A,区间区间I A. 当当x1x2时，时，

5、都有都有f(x1 ) f(x2 )，定义定义MN任意任意两个自变量的值两个自变量的值x1,x2，区间区间I内内随着随着x的增大，的增大，y也增大也增大区间区间I上从左到右上从左到右图象逐渐上升图象逐渐上升IxIy如果对于如果对于区间区间I上的上的任意任意 I 称为称为 f (x)的的单调单调增区间增区间. 那么就说那么就说 f (x)在区间在区间I上上是单调是单调增函数增函数，13Oxyx1x2f(x1)f(x2)类比增函数的研究方法定义减函数类比增函数的研究方法定义减函数. .xOyx1x2f(x1)f(x2)设函数设函数y=f(x)的定义域为的定义域为A,区间区间I A. 如果对于属于定义

6、域如果对于属于定义域A内内某个区间某个区间I上上的的任意任意两个自变量的值两个自变量的值x1,x2，设函数设函数y=f(x)的定义域为的定义域为A,区间区间I A. 如果对于属于定义域如果对于属于定义域A内内某个区间某个区间I上上的的任意任意两个自变量的值两个自变量的值x1,x2， 那么就说在那么就说在f(x)这个区间上是这个区间上是 函数函数，I称为称为f(x)的的单调单调 区间区间.增增增增当当x1x2时，时，都有都有f(x1 ) f(x2 )，当当x1x2时，时，都有都有f(x1 ) f(x2 )，减减减减 那么就说在那么就说在f(x)这个区间上是这个区间上是 函数函数，I称为称为f(x

7、)的的单调单调 区间区间.增增增增单调区间单调区间14在区间I内任取两个实数x1，x2大小相同大小相同大小相反大小相反递增递增递减递减当当x1x2时，时，都有都有f(x1 ) f(x2 )，当当x1 f(x2 )，同增同增异减异减强强调调上升趋势所对应的x的范围用区间区间表示 叫做增区间增区间；下降趋势所对应的x的范围用区间区间表示 叫做减区间减区间。15( )yf x例题例题1：根据图像指出：根据图像指出 单调增区间和单调减区间单调增区间和单调减区间单调单调增增区间是：区间是：单调单调减减区间是：区间是： 2,1,3,5 5, 2,1,316练习练习1 给出函数给出函数 y = f (x)

8、的图象，如图所示，根据的图象，如图所示，根据图象说出这个函数在哪些区间上是增函数？哪些区图象说出这个函数在哪些区间上是增函数？哪些区间上是减函数？间上是减函数？解：函数在区间解：函数在区间- -1，0，2，3上是减函数；上是减函数； 在区间在区间0，1，3，4上是增函数上是增函数23x14-1Oy练习练习2 请根据图像说明函数请根据图像说明函数 的单调性。的单调性。 1711xx2112 xxx x证明：设证明：设 任意任意x1，x2 (0,+),且且x1x2 ，则，则f (x)- f (x)例例2求证：函数求证：函数 f (x) = 在区间在区间(0，)上是减函数上是减函数1x1221121

9、21200()()0()()1( )xxxxx xf xf xf xf xf xx且即在（0,+ ）上为减函数取值取值作差作差变形变形定号定号下结论下结论18练习练习 证明函数证明函数 f(x) = 3x4在区间在区间(，+)是增函数是增函数证明：设任意证明：设任意 x1，x2 R且且x1x2，则，则 f(x1) f(x2) = (3x1+4) (3x2+4) = 3(x1 x2)121212120()()0()()( )34xxxxf xf xf xf xf xx即在（- ,+ ）上为增函数下结论下结论19判断判断2 2：函数：函数 f ( (x) )在区间在区间11，22上满足上满足 f

10、(1)(1)f(2)(2)，则函数，则函数 f ( (x) )在在1，2上是增函数上是增函数.( ).( )yxO12f(1)f(2) 判断判断1 1：函数函数 f (x)= x2 在在 是单调增函数；是单调增函数；( ), xyo2yx（1）函数单调性是针对定义域）函数单调性是针对定义域A内的某个内的某个子区间子区间I I而言的，而言的，是一个局部性质是一个局部性质,在整个定义域上不一定具有单调性在整个定义域上不一定具有单调性;（2） 、 在区间在区间I I内取任意值，不能用特殊值来代替内取任意值，不能用特殊值来代替.1x2x201.1.增函数减函数定义增函数减函数定义xOyx1x2f(x1)f(x2)齐心协力齐心协力携手共进携手共进勾心斗角勾心斗角背道而驰背道而驰