2017年高考新课标Ⅰ卷理数(解析版)

1、2017年普通高等学校招生全国统一考试（全国I 卷）理科数学注意事项：1答卷前，考生务必将自己的姓名、准考证号填写在答题卡上，2回答选择题时，选出每小题答案后，用铅笔把答题卡上对应的答案标号涂黑，如需 改动，用橡皮擦干净后，再选涂其他答案标号。回答非选择题时，将答案写在答题卡上。写 在本试卷上无效。3考试结束后，将本试卷和答题卡一并交回。一、 选择题：本题共12 小题，每小题5 分，共 60 分。在每小题给出的四个选项中，只有一项是符合题目要求的。1. 已知集合A x x 1 ， Bx 3x 1 ，则（）AABxx0BABRCABx x1DAB【答案】A【解析】A x x 1 ， Bx 3x

2、1 x x 0 A B xx 0 ， A B xx 1 ，选A2. 如图，正方形ABCD 内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白第 10 页 共 15 页色部分位于正方形的中心成中心对称，在正方形内随机取一点，则此点取自黑色部分的概率是（）AC812B设正方形边长为2，则圆半径为1则正方形的面积为2 2 4，圆的面积为 D42则此点取自黑色部分的概率为2 48故选 B3. 设有下面四个命题（）p1 ：若复数z 满足 1 R ，则 z R ；zp2：若复数z满足z2R ，则 z R ；p3 ：若复数z1 ，z2 满足z1z2R ，则 z1z2；p4：若复数zR ，则z RAp

3、1， p3Bp1，p4Cp2，p3Dp2 ，p4【答案】B1 1 a bi【解析】p1 : 设 z a bi ，则22 R ，得到 b 0 ，所以 z R .故P1 正确；1z a bi a b1p2: 若z21 ，满足 z2 R ，而 z i ，不满足z2 R ，故p2 不正确；p3: 若z1 1，z22，则z1z22，满足z1z2R ，而它们实部不相等，不是共轭复数，故p3 不正确；p4 : 实数没有虚部，所以它的共轭复数是它本身，也属于实数，故p4正确；4. 记Sn为等差数列an的前n项和，若a4a524，S648，则an的公差为（）C 4D 8A 1B 2Ca4 a5 a1 3d a1

4、 4d 2465S6 6a1d 486122a1 7d 24 联立求得16a1 15d 48 3 得 21 15 d 246d 24d4选C5. 函数 f x 在 ， 单调递减，且为奇函数若 f 11， 则满足 1 f x 2 1 的x 的取值范围是（）A2， 2B1， 1C0， 4D1， 3【答案】D【解析】因为 f x 为奇函数，所以f 1 f 11 ，于是1f x 2 1 等价于 f 1 f x 2 f 1 |又 f x 在 ， 单调递减1 x 2 11 x 3故选 D6.1x121 x 6展开式中x2 的系数为A 15B 20C.166161+ 21 x 1 1 x 2 1 xxx对

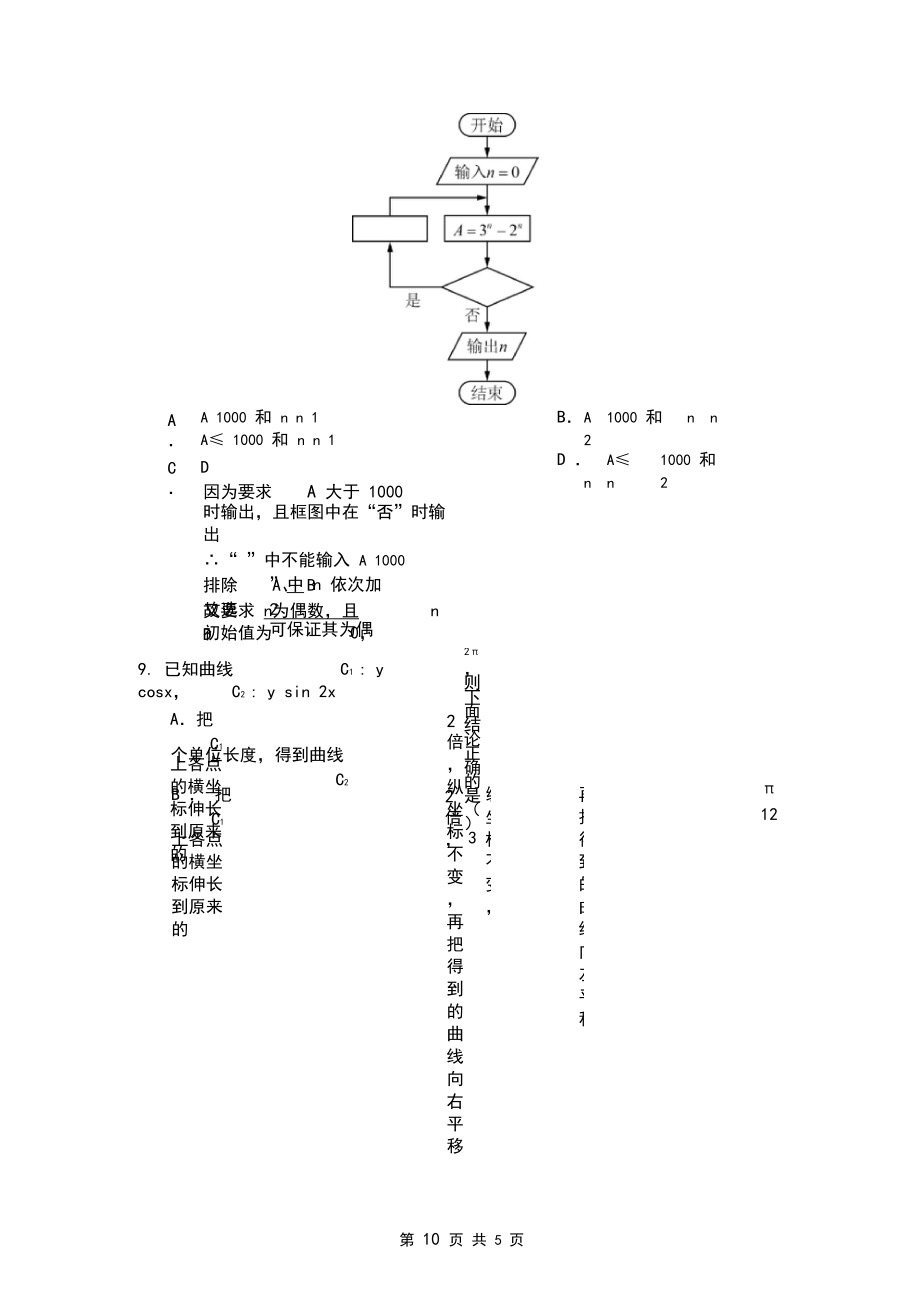
5、1 x 6的 x2 项系数为C62 625 15164对 2 1 x 的 x2项系数为C6=15，x x2 的系数为15 15 30C 30D 35故选 C7. 某多面体的三视图如图所示，其中正视图和左视图都由正方形和等腰直角三角形组成，正方形的边长为2 ，俯视图为等腰直角三角形、该多面体的各个面中有若干是梯形，这些梯形的面积之和为C 14D 16该立体图平面内只有两个相同的梯形的面S梯2 4 2 2 6S全梯6 2 128. 右面程序框图是为了求出满足 空白框中，可以分别填入故选 B3n 2n 1000的最小偶数n ， 那么在和两个ACA 1000 和 n n 1A 1000 和 n n 1

6、DBA1000 和nn2D A1000 和nn2因为要求A 大于 1000 时输出，且框图中在“否”时输出“ ”中不能输入 A 1000排除A、 B又要求 n为偶数，且n 初始值为0，”中 n 依次加 2 可保证其为偶故选 D9. 已知曲线C1 : y cosx，C2 : y sin 2x2 ，则下面结论正确的是（）3A把C1 上各点的横坐标伸长到原来的2 倍，纵坐标不变，再把得到的曲线向右平移个单位长度，得到曲线C2B 把C1 上各点的横坐标伸长到原来的2 倍，纵坐标不变，再把得到的曲线向左平移12个单位长度，得到曲线C2C 把C1 上各点的横坐标缩短到原来的1倍，2纵坐标不变，再把得到的曲

7、线向右平移个单位长度，得到曲线C2D 把C1 上各点的横坐标缩短到原来的2 倍，纵坐标不变，再把得到的曲线向左平移12个单位长度，得到曲线C2D2C1 : y cosx， C2 : y sin 2x 123首先曲线C1 、 C2 统一为一三角函数名，可将C1 : y cosx用诱导公式处理y cosx cos x22sin xsin x2 横坐标变换需将1 变成2 ，C 1上各点横 坐 标缩 短它原 来 1即 y sin x2 y sin 2x sin 2 x2242y sin 2x sin2 x 33注意 的系数，在右平移需将2 提到括号外面，这时x 平移至 x ，43根据“左加右减”原则，

8、“x ”到“ x ”需加上 ，即再向左平移 431212l2 ，直线l1 与 C 交于 A、210. 已知 F 为抛物线C ： y 4x 的交点，过F 作两条互相垂直l1 ，B 两点，直线l 2 与 C 交于 D ， E 两点，AB DE 的最小值为（）AB 14C 12D 10AK2 垂直x轴16AAF cos GF AK1 （几何关系）易知 AK1 AF （抛物线特性）GP P2PP2PAF cos P AFAFP ， BF1 cosP1 cosAB12P cos22Psin2又 DE 与 AB 垂直，即DE 的倾斜角为DE2Psin2 22P cos2而 y2 4x，即 P 2AB DE

9、 2P sin12cos12sin2cos244sin2 cos2sin cos4sin224126 16 ，当 取等号sin 24即 AB DE 最小值为16 ，故选A11. 设 x， y， z为正数，且2x 3y 5z，则（）A 2x 3y 5zB 5z 2x 3yC 3y 5z 2xD 3y 2x 5zD取对数：xln 2 y ln3 ln5x ln3 3y ln2 2 2x 3yxln 2 zln 5xln55则zln222x5z3y2x 5z，故选 D12. 几位大学生响应国家的创业号召，开发了一款应用软件，为激发大家学习数学的兴趣，他们推出了 “解数学题获取软件激活码”的活动， 这

10、款软件的激活码为下面数学问题的答案： 已知数列1, 1, 2, 1, 2, 4, 1, 2, 4, 8, 1, 2, 4, 8, 16， ,， 其中第一项是20，接下来的两项是20， 21，在接下来的三项式26， 21， 22 ，依次类推，求满足如下条件的最小整数N ： N 100 且该数列的前N 项和为2的整数幂那么该款软件的激活码是（）A 440B 330C 220D 110【答案】A【解析】设首项为第1 组，接下来两项为第2 组，再接下来三项为第3 组，以此类推设第 n 组的项数为n ，则 n 组的项数和为n 1 n2n1 n由题， N 100 ，令100 n 14 且 n N* ，即N

11、 出现在第13 组之后2第 n 组的和为1 22n 112n 组总共的和为2 1 2n n 2n 2 n12n1 n若要使前N 项和为 2 的整数幂，则N项的和 2k 1 应与 2 n 互为相反2数即 2k 1 2 n k N*， n 14k log2 n 3 n 29 ， k 529 1 29则 N5 4402故选 A二、 填空题：本题共4 小题，每小题5 分，共 20 分。13. 已知向量a ， b 的夹角为60 ， a 2， b 1 ，则 a 2b 【答案】2 3【解析】a 2b2 (a 2b)2 a2 2 a 2b cos60 2 b 2 22 2 2 2 1 224 4 4 12 a

12、 2b 12 2 3x 2y 114. 设 x， y满足约束条件2x y 1 ，则 z 3x 2y的最小值为xy0【答案】5x 2y 1不等式组2x y 1 表示的平面区域如图所示xy0由 z 3x 2y 得 y 3x z ，22求 z 的最小值，即求直线y 3 x z 的纵截距的最大值22y x z 过图中点A时，纵截距最大222x y 1x 2y 1解得 A点坐标为( 1,1)，此时 z 3 ( 1) 2 1522xy15. 已知双曲线C : 22 ， ( a 0 ， b 0 ) 的右顶点为A， 以 A为圆心，b 为半径作圆A，a2 b2圆 A与双曲线C 的一条渐近线交于M ， N 两点，

13、若MAN 60 ，则 C 的离心率为3 如图，AN AM bOA a ，MAN60 ， APb， OP OA2 PA2a23b2APtanOP3b23b24b又 tana1b2ba，解得a2 3b216. 如图，圆形纸片的圆心为O ，半径为5cm ，该纸片上的等边三角形ABC 的中心为O ，D 、 E、 F 为元 O 上的点， DBC ， ECA， FAB 分别是一BC ， CA ， AB为底边的等腰三角形，沿虚线剪开后，分别以BC ， CA ， AB 为折痕折起 DBC ， ECA， FAB ，使得 D ， E ， F 重合，得到三棱锥当 ABC 的边长变化时，所得三棱锥体积（单位：cm ）

14、的最大值为4 15由题，连接OD ，交 BC 与点 G ，由题，OD BC3OG3 BC，即OG 的长度与BC 的长度或成正比6设 OG x ，则BC 2 3x， DG 5 x三棱锥的高hDG2 OG225 10x x2 x 25 10x12S ABC 2 3 3x 3 3x 21则VS ABC h3x225 10x = 325x4 10x545534令 f x 25x4 10x5， x (0, )， f x 100x3 50x4令 f x 0 ，即 x4 2x3 0， x 2则 f x f 280则 V 380 45 体积最大值为4 15 cm31 ) ABC 面积 S3sinA2a3sin

15、 A1 bcsinA2三、 解答题：共 70 分。 解答应写出文字说明、证明过程或演算步骤。第 17-21 题为必考题，每个试题考生都必须作答。第22、 23 题为选考题，考生根据要求作答。（一）必考题：共60 分。a217. ABC 的内角 A， B， C的对边分别为a， b ， c，已知 ABC 的面积为3sin A（ 1）求sin B sin C ；（ 2）若6cos B cos C 1 ， a 3 ，求 ABC 的周长【解析】本题主要考查三角函数及其变换，正弦定理，余弦定理等基础知识的综合应用.1.且 S bcsinA2a23bcsin2232由正弦定理得sin A sin Bsin

16、Csin A ，22sin A 0 得 sinBsinC .3212)由(1)得 sin Bsin C ， cosB cosC36ABC1 cosA cos B C cos B C sin BsinC cosB cosC又 A0， 31 A 60 ， sin A ， cosA 22由余弦定理得a2 b2 c2 bc 9aa由正弦定理得b sin B ， c sin CsinAsin A2a bcsin Bsin C 8sin2 A 得 b c33a b c 333 ，即 ABC 周长为 33318. （ 12 分）如图，在四棱锥CDP 90 P ABCD 中， AB CD 中，且BAP（1）证

17、明：平面PAB平面PAD ；（2）若PA PD ABDC， APD90 ，求二面角（ 1 ）证明：BAP CDP 90 PA AB ， PD CD又 AB CD ， PD AB又 PD PA P ， PD 、 PA 平面 PAD AB 平面 PAD ，又 AB 平面 PAB平面 PAB 平面 PAD（ 2）取AD 中点 O ， BC 中点 E ，连接PO ， OEABCD四边形ABCD 为平行四边形OEAB由（1 ）知，AB平面PADOE平面PAD ，又PO 、 AD 平面 PAD OE PO ， OE AD又 PA PD ， PO AD PO 、 OE 、 AD 两两垂直以 O 为坐标原点，

18、建立如图所示的空间直角坐标系O xyz设 PA 2 ， D 2， 0， 0 、 B 2， 2， 0 、 P 0， 0， 2 、 C2， 2， 0 ， PD 2， 0，2 、 PB 2 ， 2，2 、 BC 2 2， 0， 0设 n x , y , z 为平面 PBC 的法向量n PB 0，得n BC 02x 2y 2z 02 2x 0第 11 页 共 23 页令 y 1 ，则 z 2 ， x 0，可得平面PBC 的一个法向量n 0 , 1 , 2 APD 90 ， PD PA又知 AB 平面 PAD ， PD 平面 PAD PD AB ，又 PA AB A PD 平面PAB即 PD 是平面PA

19、B 的一个法向量，PD 2 , 0 , 2cos PD , nPD n 2PD n 2 3A PB C 为钝角，所以它的余弦值为3319. （ 12 分）为了抽检某种零件的一条生产线的生产过程，实验员每天从该生产线上随机抽取16 个零件，并测量其尺寸（单位：cm ） 根据长期生产经验，可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布N ，2 （ 1） 假设生产状态正常，记 X 表示一天内抽取的16 个零件中其尺寸在3 ，3之外的零件数，求P X 1 及 X 的数学期望；（ 2）一天内抽检零件中，如果出现了尺寸在3 ，3 之外的零件，就认为这条生产线在这一天的生产过程可能出现了异常情况，

20、需对当天的生产过程进行检查（ I ）试说明上述监控生产过程方法的合理性：（ II）下面是检验员在一天内抽取的16 个零件的尺寸：9.951 0 .1 29.969.9610.019.929.981 0 . 0410.269.911 0 .1 310.029.2210.0410.059.95s 1 16 xi x 2116 xi2 16x20.212 ，其中xi 为16i1 i16 i1 iii 1， 2， 1616经计算得xxi9.97i1抽取的第i 个零件的尺寸，用样本平均数x作为 的估计值?，用样本标准差s作为的估计值?，利用估计值判断是否需对当天的生产过程进行检查，剔除? 3 ?， ?

21、3? 之外的数据，用剩下的数据估计和 （精确到0.01 ） 附：若随机变量Z 服从正态分布N ，2 ,则P 3 Z 30.997 40.997 416 0.9592，0.008 0.09 （ 1 ） 由题可知尺寸落在3 ，3 之内的概率为0.9974，落在3 ，3 之外的概率为0.0026 P X0C106 10.99740 0.9974160.9592P X11 P X 01 0.95920.0408由题可知X B 16， 0.0026E X 16 0.0026 0.0416（ 2）（ i ）尺寸落在3 ，3 之外的概率为0.0026，由正态分布知尺寸落在3 ，3 之外为小概率事件，因此上述

22、监控生产过程的方法合理（ ii ）39.97 3 0.212 9.33439.97 3 0.212 10.6063 ，39.334， 10.6069.229.334， 10.606 ， 需对当天的生产过程检查因此剔除9.22997 16 922剔除数据之后：9.97 16 9.22 10.02 152222222 9.9510.0210.12 10.029.9610.029.96 10.0210.0110.02222229.9210.029.98 10.0210.0410.0210.26 10.029.9110.021152222210.13 10.0210.02 10.0210.04 10.

23、0210.05 10.029.95 10.02 0.0080.008 0.0920. （ 12 分）P4 1，3 4222C ：x2y21 a b 0 ， 四点P11 ， 1 ，P20，1 ，P31，ab2（ 1）求（ 2）设直线 和为C 上C 的方程；l 不经过P2点且与C 相交于 A、 B 两点，若直线P2A与直线P2 B 的斜率的1 ，证明：l 过定点（ 1 ）根据椭圆对称性，必过P3 、P4又P4 横坐标为1 ，椭圆必不过P1，所以过P2，P3，P4 三点将P2 0， 1 ， P311b213 ，解得141221ab3代入椭圆方程得2代入椭圆方程得22a 4， b 1C 的方程为：2）

24、 当斜率不存在时，设kP2 AkP2ByA 1yA1mm得 m 2 ，此时 l 过椭圆右顶点，不存在两个交点，故不满足 当斜率存在时，设A x1 ， y1 ， B x2 ， y2l y kx b b 1y kx b联立 22x 4y 4 08kbx1 x22 ， x1 x221 4k1 4k21 4k2 x2 8kbx 4b2 4 04b2 4y11则k P2 Ak P2Bx1y21x2kx1bx2x1kx2bx1x2x1x2228kb2 8k 8kb2 8kb1 4k24b2 41 4k28k b 14b 1 b 11， 又 b 1b 2k 1 ，此时64k ，存在 k 使得0成立l 的方程

25、为y kx 2k 1当 x 2 时， y 1所以 l 过定点 2 ，1 21. （ 12 分）2xx已知函数f x ae a 2 e x （ 1）讨论 f x 的单调性；（ 2）若f x 有两个零点，求a的取值范围【解析】（ 1 ）由于f xae2xa 2 ex x故 f x2ae2xa 2 ex 1aex 1 2ex 1 当 a 0时，aex 1 0， 2ex 1 0从而 f x 0恒成立f x 在 R 上单调递减 当 a 0时，令 f x0，从而aex 1 0，得 x ln ax， lnalnalna，f x0fx单调减极小值单调增综上，当a 0 时，f （x） 在R 上单调递减；当 a

26、0 时，f（x） 在（, ln a）上单调递减，在（ ln a, ）上单调递增（ 2）由（1）知，当 a 0时， f x 在 R 上单调减，故f x 在 R 上至多一个零点，不满足条件1当 a 0时， fmin f ln a 1 ln a a1令ga1lna a第 10 页 共 # 页ln 1 lna a3lnf ln( 1) eaa eln a3a 2 ln 3 1313aa2 la3n1a31ln 3 10 a3故 f x 在 1 ， ln a 上有一个实根，而又ln a 1第 11 页 共 29 页故 f x 在 ln a， ln a31 上有一个实根又 f x 在 ， ln a 上单调

27、减，在ln a， 单调增，故f x 在 R 上至多两个实根3又 f x 在 1 ， ln a 及 ln a ， ln 3 1 上均至少有一个实数根，故f x 在 Ra上恰有两个实根综上， 0 a 1 10 分。请考生在第22、 23 题中任选一题作答。如果多做，则按所做的第22. 选修4-4：坐标系与参考方程x 3cos ，为参数） ，直线 l 的参数在直角坐标系xOy 中，曲线C 的参数方程为y sin ，t 为参数） xa 4t，方程为y1 t，（ 1）若a1 ，求 C 与 l 的交点坐标；（ 2）若C 上的点到l 距离的最大值为17 ，求 a （ 1） a 1 时，直线l 的方程为x 4y 3 02C 的标准方程是xy2 1 ，9x 4y 3 0联立方程x22 ，解得：9y1x3y021 x或2524 y25则 C 与 l 交点坐标是3，