高等数学：8-6 微分法在几何上的应用

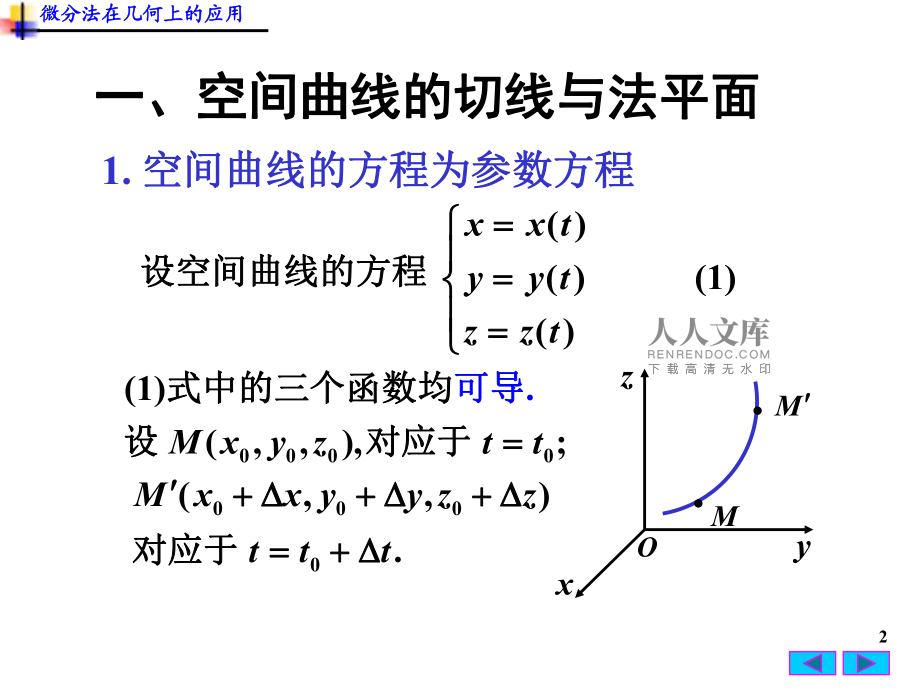
1、1小结小结 思考题思考题 作业作业空间曲线的切线与法平面空间曲线的切线与法平面曲面的切平面与法线曲面的切平面与法线第六节第六节 微分法在几何上的微分法在几何上的应用应用第八章第八章 多元函数微分法及其应用多元函数微分法及其应用2设空间曲线的方程设空间曲线的方程)1()()()( tzztyytxx(1)式中的三个函数均式中的三个函数均可导可导.M.),(0000tttzzyyxxM 对应于对应于;),(0000ttzyxM 对应于对应于设设M 1. 空间曲线的方程为参数方程空间曲线的方程为参数方程一、空间曲线的切线与法平面一、空间曲线的切线与法平面微分法在几何上的应用微分法在几何上的应用Oxy

2、z3考察割线趋近于极限位置考察割线趋近于极限位置 xxx0t t t 上式分母同除以上式分母同除以, t MM 割线割线 的方程为的方程为MM ,000zzzyyyxxx yyy0zzz 0切线的过程切线的过程微分法在几何上的应用微分法在几何上的应用Oxyz4,0,时时即即当当 tMM曲线在曲线在M处的切线方程处的切线方程)()()(000000tzzztyyytxxx 切向量切向量法平面法平面0)()()(000000 zztzyytyxxtx切线的方向向量称为曲线的切向量切线的方向向量称为曲线的切向量.过过M点且与切线垂直的平面点且与切线垂直的平面.MM 微分法在几何上的应用微分法在几何上

3、的应用Oxyz000( ( ),( ),( )Tx ty tz t5设曲线直角坐标方程为设曲线直角坐标方程为,)()(100000 xzzzxyyyxx . 0)()()(100000 zzxzyyxyxx法平面方程为法平面方程为2. 空间曲线的方程为空间曲线的方程为曲线的参数方程是曲线的参数方程是由前面得到的结果由前面得到的结果,在在M(x0, y0, z0)处处,令令)(),(xzzxyy )()(xzzxyyxx切线方程为切线方程为x为参数为参数,两个柱面两个柱面的交线的交线微分法在几何上的应用微分法在几何上的应用)()()(000000tzzztyyytxxx 6.0处的切线与法平面方

4、程处的切线与法平面方程在在 t: 求曲线求曲线 ttuezttyuuex301cossin2dcos解解2, 1, 0 zyx,costext ,sincos2tty tez33 , 1)0( x, 2)0( y3)0( z切线方程切线方程322110 zyx法平面方程法平面方程0)2(3)1(2 zyx0832 zyx)()()(000000tzzztyyytxxx 0)()()(000000 zztzyytyxxtx例例即即,0时时当当 t微分法在几何上的应用微分法在几何上的应用7例例 在抛物柱面在抛物柱面 与与 的交线上的交线上, 求对应求对应 的点处的的点处的切向量切向量.x为参数为参

5、数,于是于是 , 1 x,12xy xz24 212xz 26xy 21 x解解 22126xzxyxx所以交线上与所以交线上与21 x对应点的切向量为对应点的切向量为: T).12, 6, 1(交线的参数方程为交线的参数方程为取取微分法在几何上的应用微分法在几何上的应用8设空间曲线方程为设空间曲线方程为,0),(0),( zyxGzyxF3.空间曲线的方程为空间曲线的方程为确定了隐函数确定了隐函数(此曲线方程仍可用方程组此曲线方程仍可用方程组 两边分别对两边分别对.)()( xzzxyy )()(xzzxyyxx,0)(),(,(0)(),(,( xzxyxGxzxyxF表示表示.)x求全导

6、数求全导数:两个曲面两个曲面的交线的交线微分法在几何上的应用微分法在几何上的应用9 xydd 利用利用2.结果结果, 0dddd xzGxyGGzyxzyzyGGFFxzxzGGFFzyzyGGFFyxyxGGFF)()(100000 xzzzxyyyxx 两边分别对两边分别对,0)(),(,(0)(),(,( xzxyxGxzxyxFx求全导数求全导数 0dddd xzFxyFFzyx)()(100000 xzzzxyyyxx 微分法在几何上的应用微分法在几何上的应用ddzx10. 0)()()(000000 zzGGFFyyGGFFxxGGFFyxyxxzxzzyzy法平面方程为法平面方程

7、为,000000yxyxxzxzzyzyGGFFzzGGFFyyGGFFxx 切线方程为切线方程为,0),(0),( zyxGzyxF在点在点 M(x0, y0, z0)处的处的微分法在几何上的应用微分法在几何上的应用11解解的的在点在点求曲线求曲线)2 , 3, 1(80222222Pzyxzyx 例例 切线方程和法平面方程切线方程和法平面方程.法一法一 直接用公式直接用公式;8),(222 zyxzyxF令令222),(zyxzyxG ,2xFx ,2yFy ;2zFz ,2xGx ,2yGy .2zGz 微分法在几何上的应用微分法在几何上的应用12. 0)()()(000000 zzGG

8、FFyyGGFFxxGGFFyxyxxzxzzyzy法平面方程法平面方程,000000yxyxxzxzzyzyGGFFzzGGFFyyGGFFxx 切线方程切线方程微分法在几何上的应用微分法在几何上的应用13切线方程切线方程 1x0dd2dd22 xzzxyyx33dd0 Pxy0dd0 Pxz 法二法二 将所给方程的两边对将所给方程的两边对x求导求导的的在点在点求曲线求曲线)2 , 3, 1(80222222Pzyxzyx 切线方程和法平面方程切线方程和法平面方程.法平面方程法平面方程0)2(0)3(33)1(1 zyx. 0633 yx xzzxyyxdd2dd22 3 y2 z133 0

9、微分法在几何上的应用微分法在几何上的应用14设曲线设曲线)(),(),(tzztyytxx 证证)()(txXtx 因原点因原点)0 , 0 , 0(0)()()()()()( tztztytytxtx即即0 于是于是 )()()(222tztytx证明此曲线必在以原点为证明此曲线必在以原点为的的法平面都过原点法平面都过原点,在任一点在任一点中心的某球面上中心的某球面上.曲线过该点的法平面方程为曲线过该点的法平面方程为),(),(),(tztytx故有故有)()(tyYty )()(tzZtz 0 C)()()(222tztytx 微分法在几何上的应用微分法在几何上的应用 在法平面上在法平面上

10、,任取曲线上一点任取曲线上一点0)()()(000000 zztzyytyxxtx15yxzO 0),( zyxF 今在曲面今在曲面上任取一条上任取一条1. 设曲面设曲面的方程为的方程为0),( zyxF的情形的情形隐式方程隐式方程二、曲面的切平面与法线二、曲面的切平面与法线微分法在几何上的应用微分法在几何上的应用),(000zyxM ,),(000 zyxM 函数函数),(zyxF的偏导数在该点连续且不同的偏导数在该点连续且不同 时为零时为零. ,0tt )(),(),(000tztytx 且且点点M 对应于参数对应于参数 不全为零不全为零.过点过点M 的的曲线曲线,设其参数设其参数方程为方

11、程为),(),(),(tzztyytxx 16微分法在几何上的应用微分法在几何上的应用),(),(),(000tztytxT yxzO 0),( zyxF),(000zyxM T 由于曲线由于曲线在曲面在曲面上上, 所以所以, 0)(),(),( tztytxF 在恒等式两端对在恒等式两端对t 求全导数求全导数, 并令并令,0tt 则得则得 )(),(0000txzyxFx 若记向量若记向量),(),(),(000000000zyxFzyxFzyxFnzyx 曲线曲线在点在点M处切线的方向向量记为处切线的方向向量记为 则则式可改写成式可改写成, 0 Tn即向量即向量 Tn与与垂直垂直. . 0

12、)(),()(),(00000000 tzzyxFtyzyxFzyn17 因为曲线因为曲线是曲面是曲面上过点上过点M的的任意任意一条曲一条曲线线,所有这些曲线在点所有这些曲线在点M的切线都与同一向量的切线都与同一向量垂直垂直, 因此这些切线必共面因此这些切线必共面,称为曲面称为曲面在点在点M的的n微分法在几何上的应用微分法在几何上的应用yxzO 0),( zyxF),(000zyxM n过点过点M且垂直于切且垂直于切法线法线, ,又是法线的方向向量又是法线的方向向量.向量向量n称为曲称为曲法向量法向量. .切平面切平面,由切线形成的这一由切线形成的这一平面平面,平面的直线称为曲面平面的直线称为

13、曲面在在点点M的的面面在在点点M的的n18),(),(),(000000000zyxFzyxFzyxFnzyx 曲面在曲面在M(x0, y0 , z0)处的法向量处的法向量:微分法在几何上的应用微分法在几何上的应用切平面方程为切平面方程为0)(,()(,()(,(000000000000 zzzyxFyyzyxFxxzyxFzyx法线方程为法线方程为),(),(),(000000000000zyxFzzzyxFyyzyxFxxzyx 所以曲面所以曲面上在点上在点M的的19解解,3),(33azxyzzyxF 令令切平面方程切平面方程法线方程法线方程; 0 azx1010azayx ),0(),

14、(aazyxFFFn )3, 0 ,3(22aa 例例处的切平面处的切平面上点上点求曲面求曲面), 0(333aaazxyz ).0( a和法线方程和法线方程,3yzFx ,3xzFy ,332zxyFz )1 , 0 , 1(. ayazx0)(1)(0)0(1 azayx切平面方程为切平面方程为0)(,()(,()(,(000000000000 zzzyxFyyzyxFxxzyxFzyx法线方程为法线方程为),(),(),(000000000000zyxFzzzyxFyyzyxFxxzyx 0),(: zyxF曲面方程曲面方程MzyxFFFn),(, 曲面在曲面在M处的法向量处的法向量:微

15、分法在几何上的应用微分法在几何上的应用20842232222 yzxzxyzyx在曲面在曲面上求一点的坐标上求一点的坐标,使此点处的切平面平行于使此点处的切平面平行于yOz平面平面.解解 设所求点为设所求点为),(zyx则切平面的法向量为则切平面的法向量为)32,22,(zyxzyxzyx 由题意由题意, n)32,22,(zyxzyxzyx )0 , 0 , 1(由此得由此得022 zyx. 0,2 zyx所求之点所求之点:).0 , 2, 4()0 , 2 , 4( 及及 032 zyx),(2zyx n)(),22(2zyx )32(2zyx 微分法在几何上的应用微分法在几何上的应用21

16、2. 曲面方程形为曲面方程形为 的情形的情形),(yxfz 曲面在曲面在M处的处的切平面方程切平面方程为为, 0)()(,()(,(0000000 zzyyyxfxxyxfyx曲面在曲面在M处的处的法线方程法线方程为为.1),(),(0000000 zzyxfyyyxfxxyx,),(),(zyxfzyxF 令令,xxfF . 1 zF,yyfF 或或,)(,()(,(0000000zzyyyxfxxyxfyx )1,( yxffn显式方程显式方程微分法在几何上的应用微分法在几何上的应用),(),(),(000000000zyxFzyxFzyxFnzyx 22 例例过过上所有点处的切平面都上所

17、有点处的切平面都证明曲面证明曲面xyxez .一定点一定点 证证,),(000是曲面上任一点是曲面上任一点设设zyx0000 xyexz 则法向量为则法向量为切平面方程切平面方程为为0)()()()1(000000000 zzyyexxexyxyxy),(yxfz )1,( yxffn,)1(0000 xyexy n)(,00 xye1 微分法在几何上的应用微分法在几何上的应用230)1()1(000000000000000 zyexexyzyexexyxyxyxyxy0 0)()()()1(000000000 zzyyexxexyxyxy, 0)1(000000 zyexexyxyxy所以这

18、些平面都过所以这些平面都过00 0 xyxez 原点原点.过过上所有点处的切平面都上所有点处的切平面都证明曲面证明曲面xyxez .一定点一定点微分法在几何上的应用微分法在几何上的应用24微分法在几何上的应用微分法在几何上的应用 2003年考研数学年考研数学(一一), 3分分04222 zyxyxz与平面与平面曲面曲面平行的切平面的方程是平行的切平面的方程是( ).542 zyx25 例例 证证, 0)().( aufczbyfaxz可微可微证明曲面证明曲面)均为常数均为常数、cb的所有的所有切平面都与一常向量切平面都与一常向量平行平行.则曲面在任一点处的则曲面在任一点处的法向量法向量:,az

19、czbyfaxzyxF )(),(令令则则),( A nAbczbyfbcczbyfbcb )()(, 0 即即nA 所以所以,所有的切平面均与所有的切平面均与),(bcab 常向量常向量平行平行.0),(: zyxF曲面方程曲面方程MzyxFFFn),(, 曲面在曲面在M处的法向量处的法向量:1)( czbyf c n)(),(czbyfb ,ab取取, c b微分法在几何上的应用微分法在几何上的应用26 例例 0523zyxzyx8522222 zyx 证证85222),(22 zyxzyxF令令过直线过直线L的平面束方程为的平面束方程为523 zyx即即05)1()2()3( zyx 其

20、其法向量法向量为为)1, 2,3( ,4xFx 2 zF,4yFy 0)( zyx 微分法在几何上的应用微分法在几何上的应用求过直线求过直线L且与曲面且与曲面相切之切平面方程相切之切平面方程.27设曲面与切平面的切点为设曲面与切平面的切点为),(000zyx则则过直线过直线L的平面束方程其的平面束方程其法向量法向量为为,4xFx 2 zF,4yFy ,85222),(22 zyxzyxF tyx 21424300 05)1()2()3(000 zyx 8522202020 zyx, 3, 121 tt因而因而7, 321 微分法在几何上的应用微分法在几何上的应用)1, 2,3( 28过直线过直

21、线L的平面束方程为的平面束方程为523 zyx0)( zyx 故故所求切平面方程为所求切平面方程为7, 321 523 zyx0)(3 zyx或或523 zyx0)(7 zyx即即526 zyx或或56510 zyx微分法在几何上的应用微分法在几何上的应用298),(222 zyxzyxF令令)2 , 3, 1(2 )2 , 3, 1( 解解的的在点在点求曲线求曲线)2 , 3, 1(80222222Pzyxzyx 切线方程和法平面方程切线方程和法平面方程.应应同时垂直于同时垂直于2222228zyxzyx 和和曲面曲面 分析分析)2,3, 1()2 ,2 ,2(zyx 1n曲线在点曲线在点

22、处切线向量处切线向量 s)2 , 3, 1(0P.210nnP和和的法向量的法向量在点在点微分法在几何上的应用微分法在几何上的应用 例例 当空间当空间曲线方程为曲线方程为一般式时一般式时,求切向量曾求切向量曾采用了采用了推导推导法法.现采用现采用向量代数法向量代数法求切向量求切向量3012/snn)2, 3, 1()2 , 3, 1( )0, 4, 34( )0 ,33, 1( 令令222),(zyxzyxG )2,3, 1()2,2,2(zyx )2, 3, 1(2 )2, 3, 1( 的的在点在点求曲线求曲线)2 , 3, 1(80222222Pzyxzyx 切线方程和法平面方程切线方程和

23、法平面方程.)2 , 3, 1( 1n 2n微分法在几何上的应用微分法在几何上的应用31)(,()(,(0000000yyyxfxxyxfzzyx 的全微分的全微分在点在点函数函数),(),(00yxyxfz 因为曲面在因为曲面在M处的切平面方程处的切平面方程:全微分的几何意义全微分的几何意义,),(),(00的全微分的全微分在点在点yxyxfz 表示表示处的处的在点在点曲面曲面),(),(000zyxyxfz 切平面上的点的竖坐标的增量切平面上的点的竖坐标的增量.切平面切平面上点的上点的竖坐标竖坐标的增量的增量微分法在几何上的应用微分法在几何上的应用32),(00yxffxx ),(00yx

24、ffyy 其中其中,1cos22yxxfff ,1cos22yxyfff .11cos22yxff (, 1)(,1)xyxyffnff 或法向量法向量 ,若若表示曲面的法向量的方向角表示曲面的法向量的方向角,并假定并假定法向量的方向是向上法向量的方向是向上的的,即使得它与即使得它与z 轴的正向所成的角轴的正向所成的角 是是锐角锐角, 则法向量的则法向量的方向余弦为方向余弦为n微分法在几何上的应用微分法在几何上的应用33因为因为(第三个分量为负第三个分量为负), 求旋转抛物面求旋转抛物面 在任意点在任意点P(x, y, z)处处向上向上的法向量的法向量(即与即与z轴夹角为锐角轴夹角为锐角的法向

25、量的法向量).122 yxz解解, 1),(22 yxyxf而而Pyxff)1,( )1,2 ,2( yx).1 ,2,2(yx 为为向下向下的法向量的法向量故故向上向上的法向量应为的法向量应为:微分法在几何上的应用微分法在几何上的应用341993年研究生考题年研究生考题,填空填空,3分分轴旋转一周轴旋转一周绕绕由曲线由曲线yzyx 0122322)2, 3, 0(解解12233222 yzx令令12323),(222 zyxzyxF)2,3,0(),(zyxFFF )26, 34, 0( )3, 2, 0(51 )2,3,0()6 ,4 ,6(zyx )3, 2, 0(51n|0nnn 微分法在几何上的应用微分法在几何上的应用得到