第三讲：线性规划

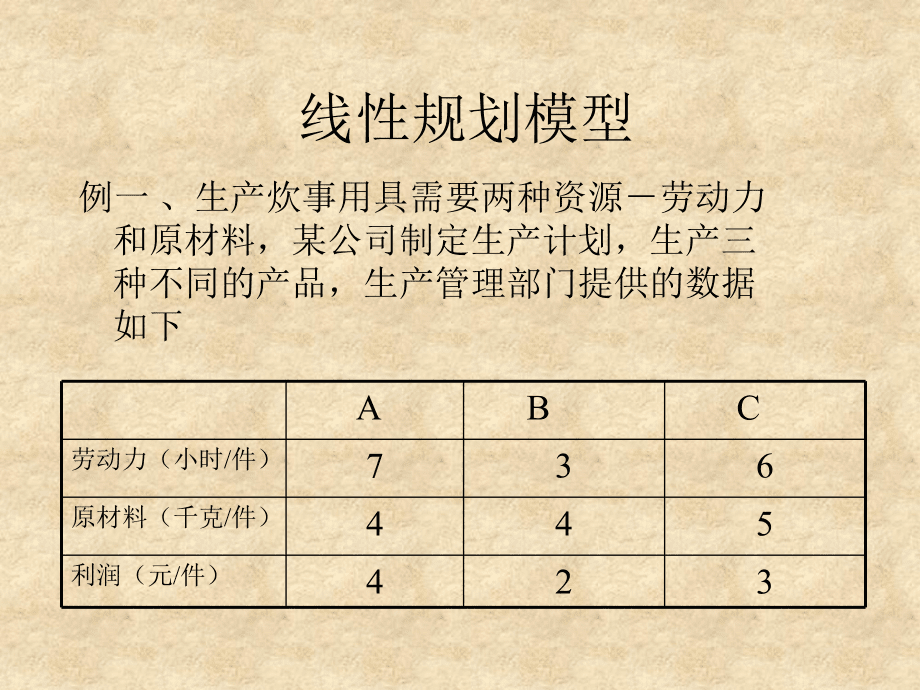
1、 线性规划 优化问题，一般是指用“最好”的方式，使用或分配有限的资源，即劳动力、原材料、机器、资金等，使得费用最小或利润最大. 建立优化问题的数学模型 1) 确定问题的决策变量 2) 构造模型的目标函数和允许取值的范围，常用一组不等式来表示.T1min(max)( ),(,)s.t.( )0,1,2,nizf xxxxgxim或（1）（2）由（1）、（2）组成的模型属于约束优化，若只有（1）式就是无约束优化，f(x)称为目标函数，g(x)称为约束条件若目标函数f(x)和约束条件g(x)都是线性函数，则称该模型是线性规划. 线性规划模型例一 、生产炊事用具需要两种资源劳动力和原材料，某公司制定生

2、产计划，生产三种不同的产品，生产管理部门提供的数据如下 A B C劳动力（小时/件）736原材料（千克/件）445利润（元/件）423每天供应原材料200kg，每天可使用的劳动力为150h. 建立线性规划模型，使总收益最大，并求各种产品的日产量. 解解 第一步,确定决策变量. 用 分别表示A, B, C三种产品的日产量 第二步, 约束条件 原材料： 劳动力： 第三步，确定目标函数 AxBxCx445200ABCxxx736150ABCxxx423ABCZxxx例2 一家广告公司想在电视、广播上做广告，其目的是尽可能多的招来顾客，下面是调查结果： 电视无线电 广播杂志白天最佳时间一次广告费用（千

3、元）40753015受每次广告影响的顾客数（千人）400900500200受每次广告影响的女顾客数（千人）300400200100这家公司希望广告费用不超过800（千元）还要求：1）至少要有200万妇女收看广告；2）电视广告费用不超过500（千元） 3）电视广告白天至少播出3次，最佳时间至少播出2次；4）通过广播、杂志做的广告要重复5到10次.123412341234121234m ax400900500200407530158003004002001002000. .40755003,2,510,510Zxxxxxxxxxxxxs txxxxxx令 分别白天，最佳电视、广播、杂志广告次数 1

4、234,xxxx，线性规划问题的求解在理论上有单纯形法，在实际建模中常用以下解法： 1. 图解法 2. LINGO 软件包； 3. Excel中的规划求解； 4. MATLAB软件包.3.2 用用MATLAB优化工具箱解线性规划优化工具箱解线性规划min z=cX s.t.AXb1. 模型：命令：x=linprog（c, A, b） 2. 模型：min z=cX s.t.AXbbeqXAeq命令：x=linprog（c，A，b，Aeq,beq）注意：若没有不等式： 存在，则令A= ，b= .bAX 3. 模型：min z=cX s.t.AXbbeqXAeqVLBXVUB命令：1 x=linpr

5、og（c，A，b，Aeq,beq, VLB，VUB） 2 x=linprog（c，A，b，Aeq,beq, VLB，VUB, X0） 注意：1 若没有等式约束: , 则令Aeq= , beq= . 2其中X0表示初始点 beqXAeq4. 命令：x,fval=linprog()返回最优解及处的目标函数值fval.问题一问题一 ： 任务分配问题：某车间有甲、乙两台机床，可用于加工三种工件.假定这两台车床的可用台时数分别为800和900，三种工件的数量分别为400、600和500，且已知用三种不同车床加工单位数量不同工件所需的台时数和加工费用如下表.问怎样分配车床的加工任务，才能既满足加工工件的要

6、求，又使加工费用最低？ 单位工件所需加工台时数 单位工件的加工费用 车床类 型 工件1 工件2 工件3 工件1 工件2 工件3 可用台时数 甲 0.4 1.1 1.0 13 9 10 800 乙 0.5 1.2 1.3 11 12 8 900 两个引例两个引例解解 设在甲车床上加工工件1、2、3的数量分别为x1、x2、x3，在乙车床上加工工件1、2、3的数量分别为x4、x5、x6,可建立以下线性规划模型： 解答问题二：问题二： 某厂每日8小时的产量不低于1800件.为了进行质量控制，计划聘请两种不同水平的检验员.一级检验员的标准为：速度25件/小时，正确率98%，计时工资4元/小时；二级检验员

7、的标准为：速度15件/小时，正确率95%，计时工资3元/小时.检验员每错检一次，工厂要损失2元.为使总检验费用最省，该工厂应聘一级、二级检验员各几名？解解 设需要一级和二级检验员的人数分别为x1、x2人,则应付检验员的工资为：212124323848xxxx因检验员错检而造成的损失为：21211282)%5158%2258(xxxx故目标函数为：故目标函数为：2121213640)128()2432(minxxxxxxz约束条件为：0, 0180015818002581800158258212121xxxxxx线性规划模型：线性规划模型：213640minxxz12121253459s.t.

8、150,0 xxxxxx 解答返 回线性规划模型的一般形式线性规划模型的一般形式11min,1,2,., .s.t.0,1,2,., .ni iinik kikiucxa xb inxin 目标函数和所有的约束条件都是设计变量目标函数和所有的约束条件都是设计变量的线性函数的线性函数.min. s.tucxAxbvlbxvub矩矩阵阵形形式式：实际问题中实际问题中的优化模型的优化模型T1min(max)( ),(,)s.t.( )0,1,2,nizf xxxxg xim或x是决策变量是决策变量f(x)是目标函数是目标函数gi(x) 0是约束条件是约束条件数学规划数学规划线性规划线性规划(LP)二

9、次规划二次规划(QP)非线性规划非线性规划(NLP)纯整数规划纯整数规划(PIP)混合整数规划混合整数规划(MIP)整数规划整数规划(IP)0-1整数规划整数规划一般整数规划一般整数规划连续规划连续规划 优化模型的分类优化模型的分类解解 编写编写M文件文件xxgh1.m如下：如下：c=-0.4 -0.28 -0.32 -0.72 -0.64 -0.6; A=0.01 0.01 0.01 0.03 0.03 0.03;0.02 0 0 0.05 0 0;0 0.02 0 0 0.05 0;0 0 0.03 0 0 0.08; b=850;700;100;900; Aeq=; beq=; vlb=

10、0;0;0;0;0;0; vub=;x,fval=linprog(c,A,b,Aeq,beq,vlb,vub) To MATLAB (xxgh1)解解: 编写编写M文件文件xxgh2.m如下：如下： c=6 3 4; A=0 1 0; b=50; Aeq=1 1 1; beq=120; vlb=30,0,20; vub=; x,fval=linprog(c,A,b,Aeq,beq,vlb,vub)To MATLAB (xxgh2)123m in( 634 )xzxx32120030 xxx1231111 2 0s .t. 0105 0 xxxs.t.Xz8121110913min 900800

11、3 . 12 . 15 . 000000011 . 14 . 0X改写为：例例3 问题一的解答 问题问题编写编写M文件文件xxgh3.m如下如下:f = 13 9 10 11 12 8;A = 0.4 1.1 1 0 0 0 0 0 0 0.5 1.2 1.3;b = 800; 900;Aeq=1 0 0 1 0 0 0 1 0 0 1 0 0 0 1 0 0 1;beq=400;600;500;vlb = zeros(6,1);vub=;x,fval = linprog(f,A,b,Aeq,beq,vlb,vub)To MATLAB (xxgh3)结果结果:x = 0.0000 600.00

12、00 0.0000 400.0000 0.0000 500.0000fval =1.3800e+004 即在甲机床上加工600个工件2,在乙机床上加工400个工件1、500个工件3，可在满足条件的情况下使总加工费最小为13800.例例2 问题二的解答 问题问题 213640minxxz s.t. )45(3521xx改写为：编写编写M文件文件xxgh4.m如下：如下：c = 40;36;A=-5 -3;b=-45;Aeq=;beq=;vlb = zeros(2,1);vub=9;15; %调用linprog函数：x,fval = linprog(c,A,b,Aeq,beq,vlb,vub)To MATLAB (xxgh4)结果为：结果为：x = 9.0000 0.0000fval =360即只需聘用9个一级检验员. 注：注：本问题应还有一个约束条件：x1、x2取整数.故它是一个整数线性规划整数线性规划问题.这里把它当成一个线性规划来解，求得其最优解刚好是整数：x1=9，x2=0，故它就是该整数规划的最优解.若用线性规划解法求得的最优解不是整数，将其取整后不一定是相应整数规划的最优解，这样的整数规划应用专门的方法求解.返 回实验作业实验作业 某厂生产