人教版八年级上册数学课件 12.2 第2课时 “边角边”(共24张PPT)

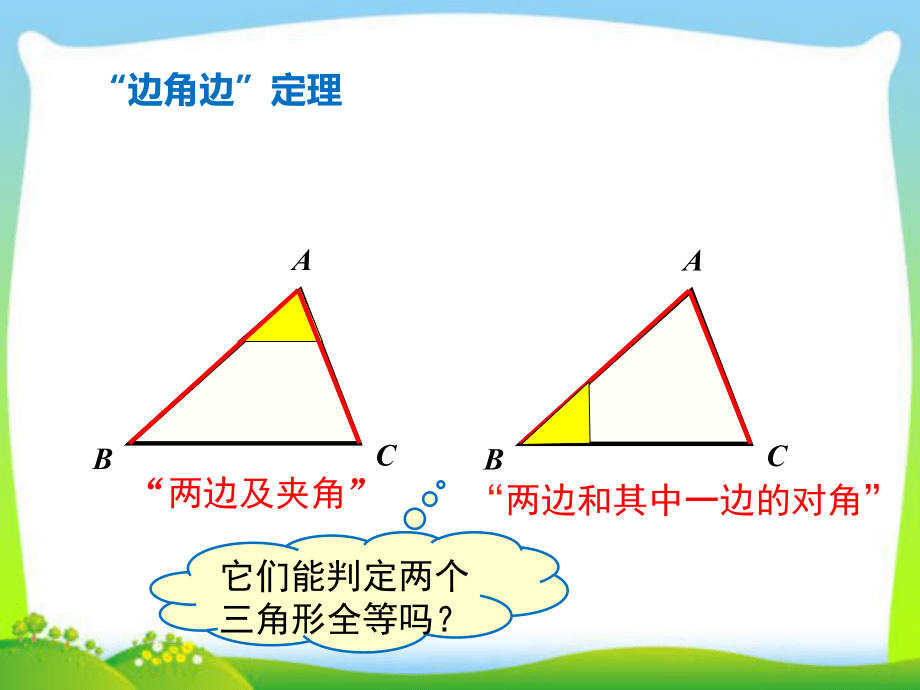
1、第2课时 边角边葫芦岛第六初级中学葫芦岛第六初级中学“边角边”定理ABCABC“两边及夹角”“两边和其中一边的对角”它们能判定两个三角形全等吗？ 动手试一试：动手试一试：尺规作图画出一个ABC，使ABAB，ACAC，AA （即使两边和它们的夹角对应相等）. 把画好的ABC剪下，放到ABC上，它们全等吗？A B C SASSAS能否判定的两个三角形全等能否判定的两个三角形全等? ?A B C A D E B C 作法：（1）画DAE=A；（2）在射线AD上截取AB=AB,在射线AE上截取AC=AC；（3）连接BC .思考： A B C 与 ABC 全等吗？如何验证？这两个三角形全等是满足哪三个条

2、件？在ABC 和 DEF中，ABC DEF（SAS）文字语言：文字语言： 两边和它们的夹角分别相等的两个三角形全等（简写成“边角边”或“SAS ”） “边角边”判定方法几何语言：几何语言：AB = DE，A =D，AC =AF ，A B C D E F 必须是两边“ 夹 角 ” 如果AB=CB ， ABD= CBD，那么 ABD 和 CBD 全等吗？分析: ABD CBD边:角:边: :AB=CB(已知)ABD= CBD(已知)ABCD(SAS)BD=BD(公共边)证明： 在ABD 和 CBD中，AB=CB，ABD= CBD， ABDCBD ( SAS).BD=BD，例1【变式1】已知：如图,

3、AB=CB,1= 2. 求证:(1) AD=CD； (2) DB 平分 ADC.ADBC1243在ABD与CBD中，证明:ABDCBD（SAS），AB=CB ，1=2 ，BD=BD （公共边），AD=CD，3=4，DB 平分 ADC.ABCD【变式2】已知:AD=CD，DB平分ADC ， 求证:A=C.12在ABD与CBD中，证明:ABDCBD（SAS），AD=CD，1=2，BD=BD （公共边），A=C.DB 平分 ADC，1=2. 如图，有一池塘，要测池塘两端A、B的距离，可先在平地上取一个可以直接到达A和B的点C，连接AC并延长到点D，使CDCA，连接BC并延长到点E，使CECB连接DE

4、，那么量出DE的长就是A、B的距离，为什么?CAEDB例2CAEDB证明：在ABC 和DEC 中，ABC DEC（SAS），），AB =DE（全等三角形的对应边相等）.AC = DC，ACB =DCE （对顶角相等），），CB=EC ， 归纳：归纳：证明线段相等或者角相等时，常常通过证明它们是全等三角形的对应边或对应角来解决.【跟进训练】已知:如图, AB=DB,CB=EB,12，求证:A=D.证明: 12， 1+DBC 2+ DBC(等式的性质)， 即ABCDBE. 在ABC和DBE中, ABDB， ABCDBE， CBEB， ABCDBE(SAS). A=D.1A2CBDE 如图，把一长一

5、短的两根木棍的一端固定在一起，摆出ABC.固定住长木棍，转动短木棍，得到ABD.这个实验说明了什么？B A CDABC和ABD满足AB=AB ,AC=AD,B=B,但ABC与ABD不全等.SSASSA能否判定两个三角形全等？能否判定两个三角形全等？ 画一画：画ABC 和DEF，使B =E =30， AB =DE=5 cm ，AC =DF =3 cm 观察所得的两个三角形是否全等？ ABMCDABCABD结论：有两边和其中一边的对角分别相等的两个三角形不一定全等. 下列条件中，不能证明ABCDEF的是()AABDE，BE，BCEFBABDE，AD，ACDFCBCEF，BE，ACDFDBCEF，C

6、F，ACDF解析：要判断能不能使ABCDEF，应看所给出的条件是不是两边和这两边的夹角，只有选项C的条件不符合，故选C.C方法总结：判断三角形全等时，注意两边与其中一边的对角相等的两个三角形不一定全等解题时要根据已知条件的位置来考虑，只具备SSA时是不能判定三角形全等的例31.在下列图中找出全等三角形进行连线.?308 cm9 cm?308 cm8 cm8 cm5 cm30?8 cm5 cm308 cm?5 cm8 cm5 cm?308 cm9 cm?308 cm8 cm2.如图，AB=DB，BC=BE，欲证ABEDBC，则需要增加的条件是 ( ) A.AD B.EC C.A=C D.ABDE

7、BC D3.如图，点E、F在AC上，AD/BC，AD=CB，AE=CF. 求证：AFDCEB. FABDCE证明：AD/BC， A=C，AE=CF，在AFD和和CEB中，AD=CB，A=C，AF=CE， AFDCEB（SAS）.AE+EF=CF+EF， 即 AF=CE. 4.已知：如图，AB=AC,AD是ABC的角平分线， 求证：BD=CD.证明：AD是ABC的角平分线， BAD=CAD.在ABD和ACD中，AB=AC，BAD=CAD，AD=AD， ABDACD（SAS）. BD=CD.【变式1】已知：如图，AB=AC, BD=CD， 求证： BAD= CAD.证明： BAD=CAD.在ABD

8、和ACD中，ABDACD（SSS），AB=AC，BD=CD，AD=AD， 【变式2】如图，AB=AC, BD=CD，E为AD上一点， 求证： BE=CE.证明： BAD=CAD.在ABD和ACD中，AB=AC，BD=CD，AD=AD， BE=CE.在ABE和ACE中，AB=AC，BAD=CAD，AE=AE， ABDACD（SSS）.ABEACE（SAS）.【拓展】如图，已知CA=CB,AD=BD, M、N分别是CA、CB的中点，求证：DM=DN.在ABD与CBD中，证明:CA=CB ，AD=BD ，CD=CD ，ACDBCD（SSS），连接CD，如图所示.A=B.又M、N分别是CA、CB的中点，AM=BN.在AMD与BND中，AM=BN ，A=B，AD