函数y＝Asin（ωx＋φ）的图象

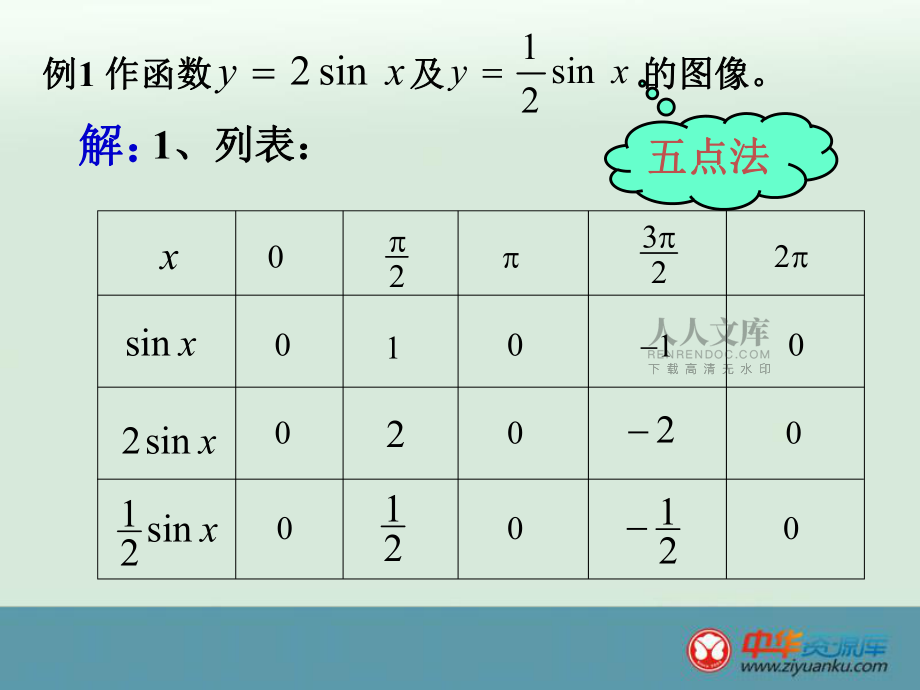
1、函数函数y yAsinAsin（xx）的图象）的图象1、列表：、列表：02322xxsin2xsin21xsin10001002210002210例例1 作函数作函数 及及 的图像。的图像。 xysin21xysin2解：解：五点法五点法yox222312-1-2y=2sinxysinx21y sinx想一想想一想? ?什么发生什么发生了变化了变化2. 描点、作图：描点、作图：归纳总结：归纳总结：函数函数 的图像可以看作是把的图像可以看作是把 的图像上所有的图像上所有点的纵坐标伸长（当点的纵坐标伸长（当A1A1时）或缩短（当时）或缩短（当0A10A0时）或向右（当 0时）平行移动 个单位长度而

2、得到的。)sin(xyxysin|课 堂 练 习1、为得到为得到sin(2x+)，x R，的图，的图像像，只，只需将函数需将函数2sin(2x+)，x R的图的图像像上所有上所有点点( ) (A)横坐标变为原来的倍，纵坐标不变横坐标变为原来的倍，纵坐标不变 (B)横坐标变为原来的倍，纵坐标不变横坐标变为原来的倍，纵坐标不变 (C)纵坐标变为原来的倍，横坐标不变纵坐标变为原来的倍，横坐标不变 (D)纵坐标变为原来的倍，横坐标不变纵坐标变为原来的倍，横坐标不变213213C2、将函数、将函数y=3sinx的图像向右平移的图像向右平移 个单位长度，得到函数的解析式个单位长度，得到函数的解析式为为:

3、。 4)4sin(3xy3、为得到函数、为得到函数sin(2x- ),x R，的图，的图像像，只需将函数只需将函数sin2x, x R，的图，的图像像上所上所有点有点( )(A)向左平移向左平移 个单位长度个单位长度(B)向右平移向右平移 个单位长度个单位长度(C)向左平移向左平移 个单位长度个单位长度(D)向右平移向右平移 个单位长度个单位长度36633B练习：练习：已知函数已知函数y=3sin(x+y=3sin(x+/5)xR/5)xR的图象为的图象为C. C. (1)为了得到函数为了得到函数y=3sin(x-/5)，xR的图象，只的图象，只需把需把C上所有的点上所有的点向右平行移动向右平

4、行移动2/5个单位长度个单位长度 (2)为了得到函数为了得到函数y=4sin(x+/5)，xR的图象，只的图象，只需把需把C上所有的点上所有的点 纵坐标伸长到原来的纵坐标伸长到原来的4/3倍，倍，横坐标不变横坐标不变1. 列表：xx2x2sin424301000123220例例3 作函数作函数 及及 的图像。的图像。 xy21sinxy2sinxyO2122132. 描点：x21siny 对于函数1. 列表：2. 描点：xyO21134xx21x21sin2322042430由例 3 可以看出，在函数 中， 决定了函数 的周期 ，通常称周期的倒数 为频率。 )0(sinxy2T21Tf小结：函

5、数 的图像，可以看作是把 的图像上所有点的横坐标缩短（当 时）或伸长（当 时）到原来的倍（纵坐标不变）而得到的。 )0(sinxyxysin1011问题：函数 的图像能否由函数 的图像变化而得到呢？应该作怎样的变化呢？1, 0)(xfy)(xfy 1101)(xfy 小结：函数 的图像，可以看作是把 的图像上所有点的横坐标缩短（当 时）或伸长（当 时）到原来的 倍（纵坐标不变）而得到的。 1, 0)(xfy解：例4：画出函数 和函数 的简 图。1)62sin(3xyxysin（1）列表xxysin022320001162xx)62sin(x126125321211022321)62sin(3x

6、y0101014121（2）描点和作图）描点和作图问题：可不可以由函数 的图像而得到函数 的图像？如果可以，请给出过程。1)62sin(3xyxysin变换过程变换过程先画出 的图像；xysin从 的图像上各点的横坐标变为原来的 倍,得到函数 的图像；xysin1xysin把所得到的曲线向左（右）平移 个单位长度，得到函数 的图像；|)sin(xy把曲线上各点的纵坐标变为原来的 倍，这时的 曲线就是函数 的图像；A)sin(xAy把图像向上（下）平移 个单位长度，得 的图像.|bbxAy)sin(问题：可不可以由函数 的图像而得到函数 的图像？如果可以，请给出过程。)0,0)(sin(AxAy

7、xysin方法：先画出 的图像；xysin把正弦曲线向左（右）平移 个单位长度，得 到函数 的图像；|)sin(xy使曲线上各点的横坐标变为原来的 倍，得到函数 的图像；1)sin(xy把曲线上各点的纵坐标变为原来的 倍，这时的曲线就是函数 的图像；A)sin(xAy把图像向上（下）平移 个单位长度，得 的图像.|bbxAy)sin(方法二：方法 三：先画出 的图像；xysin把图像上各点的横坐标变为原来的 倍,得到函数 的图像；1xAysin把正弦曲线上各点的纵坐标变为原来的 倍，这时的曲线就是函数 的图像；AxAysin把所得到的曲线向左（右）平移 个单位长度，得到函数 的图像；|)sin

8、(xAy把图像向上（下）平移 个单位长度，得 的图像.|bbxAy)sin(方法四：先画出 的图像；xysin把正弦曲线上各点的纵坐标变为原来的 倍，这时的曲线就是函数 的图像；AxAysin把曲线向左（右）平移 个单位长度，得 到函数 的图像；|)sin(xAy使曲线上各点的横坐标变为原来的 倍，得到函数 的图像；1)sin(xAy把图像向上（下）平移 个单位长度，得 的图像.|bbxAy)sin(课课 堂堂 练练 习习1、为得到为得到sin(x - )，x R，的图，的图像像，只，只需将函数需将函数sin(x)，x R的图的图像像上所有点上所有点( )(A)横坐标变为原来的倍，纵坐标不变横

9、坐标变为原来的倍，纵坐标不变(B)横坐标变为原来的倍，纵坐标不变横坐标变为原来的倍，纵坐标不变(C)纵坐标变为原来的倍，横坐标不变纵坐标变为原来的倍，横坐标不变(D)纵坐标变为原来的倍，横坐标不变纵坐标变为原来的倍，横坐标不变213321212、将函数、将函数y=2sin（x+）的图像上）的图像上所有点的横坐标变为原来的倍，所有点的横坐标变为原来的倍，纵坐标不变，得到的函数的解析纵坐标不变，得到的函数的解析式为式为: 。 5)52sin(2xy3、将函数、将函数y=sinx的图像上所有点的横坐标变为的图像上所有点的横坐标变为原来的倍，纵坐标不变，再将所得函数图原来的倍，纵坐标不变，再将所得函数

10、图像向左平移像向左平移 个单位长度，得到的函数的解个单位长度，得到的函数的解析式为析式为: 。6)6(31sinxy练习1：使函数 图像上每一点的纵坐标保持 不变，横坐标缩小到原来的 倍，然后再将其图像沿 x 轴向左平移 个单位得到的曲线与 的图像相同，则 的表达式为_)(xfy 216xy2sin)(xf解：由题意可得个单位向右平移62sinxy)32sin()6(2sinxxy倍，纵坐标不变横坐标伸长到原来的2)3sin(xy练习2：如下图，它是函数 的图像，根据图中数据，写出该函数解析式。),0, 0)(sin(AxAy |xy55O425解：由图像可知，3)25(2, 5TA于是，32

11、322T所以，)32sin(5xy将最高点坐标)5,4(代入)32sin(5xy得：5)6sin(5),(226Zkk),(32Zkk3取)332sin(5xy该函数的解析式为练习3：如下图，某地一天从6时到14时的温度变化曲线近似满足（1）求这段时间的最大温差；（2）写出这段曲线的函数解析式。bxAy)sin( 时间/h 温度 / 0 C 30 20 10 14 10 6 o y x解：C20)1 (20,10)2(bA20)8sin(1082161686142xyTT)(232681020)68sin(10),10, 6(Zkk即所以因为函数过点14, 6,20)438sin(10,43, 0 xxyk该函数的解析式为则取例例 1 1 求下列函数的最大值、最小值，以及达求下列函数的最大值、最小值，以及达到达到最大值、最小值时到达到最大值、最小值时x x的集合。的集合。)43cos(21)3(21sin34)2(2sin1xyxyxy）（例例 2 2)321sin(2xy(1)(1)求函数求函数 的递增区间。的递增区间。 )654cos(31xy(2)(2)求函数求函数 的递减区间。的递减