2021年2月广东省高三六校第3次联考数学试题和答案

1、2021届广东省六校第三次联考数学试题一、单项选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项 中，只有一项是符合题目要求的。D. xl0<x<4 )1.已知集合4 = "1/<4,8 = *1*>0,则408=(A. x0<x<2 B. xx>-2 C. xl-2<x<0)2.已知复数z满足(l + i)z = (l i),则复数z的模|z|=(第13页共12A. 0B. 1C. 72D. 23.做志愿者参与社区服务是学生参加社会公益活动的主要途径.某个星期日有4名学生志 愿者随机平均分配到A、B两个社区进行垃

2、圾分类宣传活动，则其中甲乙两人都被分配到A社区的概率是（）A1D1A. -D. 一24D- IB. -20展开式中常数项是（）C. 40匹5.使得“X>1 ”成立的一个必要且不充分的条件是（D. -40M )A.%2 > 1B. %3 > 16.已知/(x) =A. 3|log2x|-|sin.v|, 0<x<2/(x-2),x>2B. 4,则/（x）在（0,2乃）上的零点个数是（）C. 5D. 67.随着国家对环保的重视，地方政府积极兴建生活垃圾无害化处理厂。下表是近年 来广东省的数据表：注： 年份代号t从18分别对应年份20122019害化处理厂数量为（

3、/-I）（结果四舍五入）用线性回归方程模型y = a + bt拟合垃圾处理厂数量y与年份代号t的关系，用公式计算得B才7.50,相关系物力0.96, Z»= 620,据此可估计2022年广东市辖区生活垃圾无A. 118B. 126C. 129D. 1348 .已知抛物线V=-4x的焦点为尸，过户的直线1与圆/ + 丁=5交于M.N两点，则 丽丽的值是()A. -4B. -5C. 4D.不确定的二、多项选择题：本题共4小题，每小题5分，共20分。在每小题给出选项中，有 多项符合题目要求，全部选对的得5分，部分选对的得2分，有选错的得。分。9 .已知空间中异而直线4所成的角为60。，若过

4、空间中某点A的直线，与所成的角都 为氏则()A.满足8 = 30直线1有且只有1条 B.满足6 = 60°的直线，有且只有1条C.满足6 =90°的直线，有且只有1条 D. 0 e 30°,90°10 .已知函数/(x) = cos(x + )COS(X),贝Ij ()44A. /(x)是周期为江的周期函数B. /(x)的值域是C.将/")的图像向左平移2个单位长度后，可得一个奇函数的图像4D. /*)在0,|上单调递增11 .若 Ovva v 巳，贝 ij ()2A. ea + b> eh + aB. aeh + a> bea +

5、 beeC. baa + a>anb+bD. asnb+a>bsna+b12 .大衍数列来源于乾坤谱中对易传“大衍之数五十”的推论，主要用于解释中 国传统文化中的太极衍生原理。如图示，数列中的每一项，都代表太极衍生过程中曾 经经历过的两仪数量总和，其前10项依次是0,2,4,8,128,24,32,40,50,，此数列记 为,其前项的和记为5，则()三、填空题：本题共4小题，每小题5分，共20分。13 .函数/（x） = 2x + cosx在点4）处的切线与两坐标轴围成的三角形而积是14 .利用计算机绘制函数图象时可以得到很多美丽的图形，图象形似右图所示的函数称为m型函数，写出一个

6、定义域为-2,2且值域为。,2的m型函数是.（116.已知双曲线E:72工上a2 b2=1的两焦点分别为"，F?,过右焦点F2的直线与双曲线七交15 .九章算术是我国古代数学名著，它在几何学中的研究比西方 早一千多年，书中将四个而都为直角三角形的四而体称为鳖席. 在鳖膈ABCD的四个直角三角形中，8。是RtABAD和 RtABCD的斜边，且所有直角三角形斜边长分别为AO =区 BC =屈,8。= JiZ,它的所有顶点都在球。的球而上，则 球。的体积为.于A3两点，若丽=29且A48G为等腰三角形，则双曲线E的离心率为 四、解答题：本题共6小题，共70分。解答应写出文字说明、证明过程或

7、演算步骤。17. （10 分）在% =2%，4一 =4,心=6这三个条件中任选一个，补充在下面问题中, 若问题中正整数k存在，求k的值；若问题中的正整数k不存在，说明理由.问题：已知等差数列%的前八项和为5“，各项为正的等比数列4的前项和为， 7；=2M=2, $3=4,且，是否存在正整数k使成立？注：如果选择多个条件分别解答，按第一个解答计分.18. （12 分）在AA3C中，内角4仇。的对边分别为。，为c,。= J5csinB+bcosC,点。为A3边上一点，AD = 2BD = 2,CD = W.（1）求B;（2）求MBC的面积.19. （12 分）某企业办有甲乙两个工厂，为了解其工人的

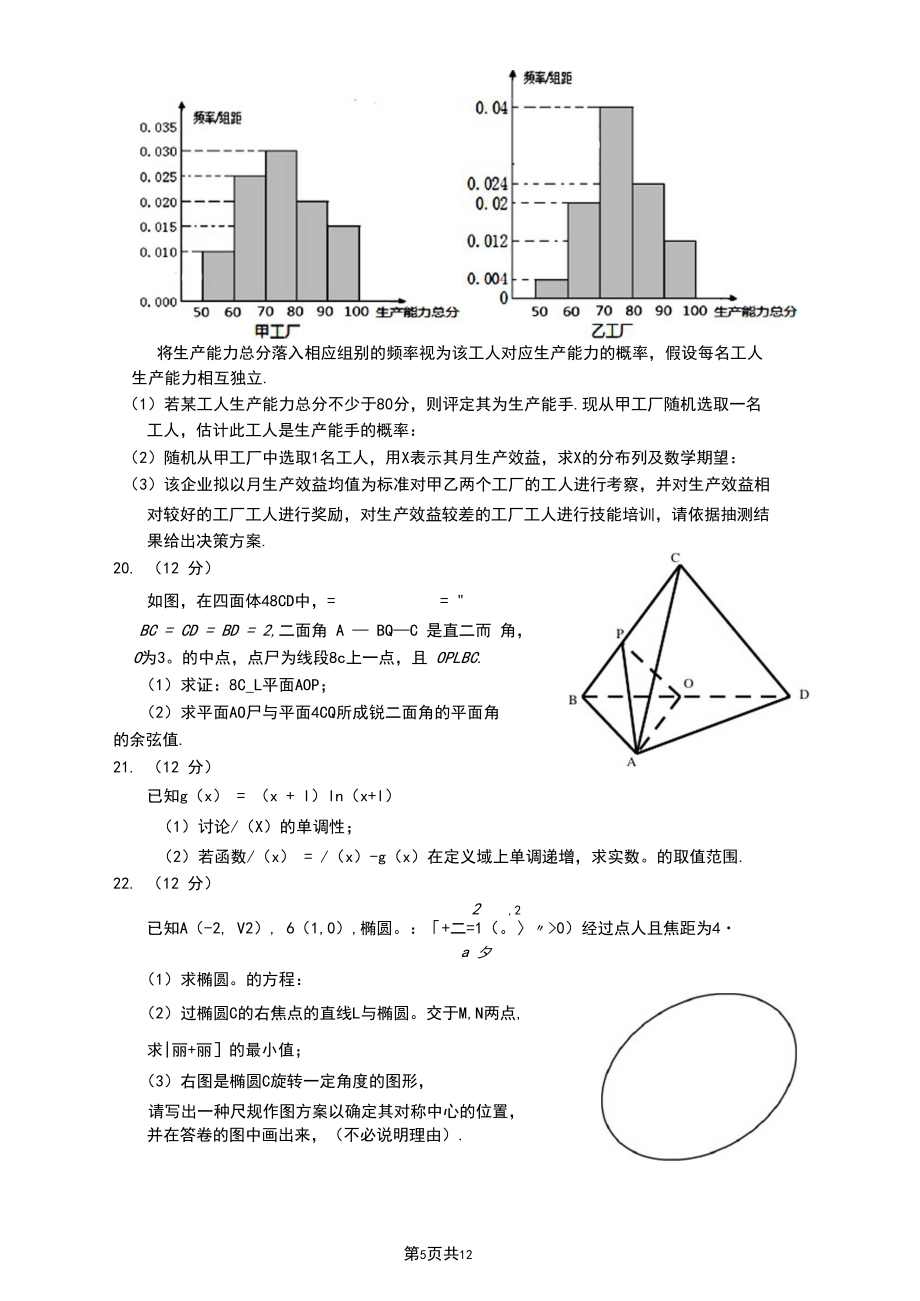
8、生产能力以及生产效益情况，现用分层抽样 的方法，分别从甲乙两个工厂的工人中抽取100名、50名进行测评，并根据5项最重 要的指标评分合计出每名工人的生产能力总分.由测评可知，工人月生产效益与生产能 力密切相关，统计结果如下表：生产能力总分（分）0, 60)60, 70)70, 80)80, 90)90, 100月生产效益阮）1000015000200002500030000工人的生产能力总分测评结果统计如下:将生产能力总分落入相应组别的频率视为该工人对应生产能力的概率，假设每名工人 生产能力相互独立.（1）若某工人生产能力总分不少于80分，则评定其为生产能手.现从甲工厂随机选取一名 工人，估计

9、此工人是生产能手的概率：（2）随机从甲工厂中选取1名工人，用X表示其月生产效益，求X的分布列及数学期望：（3）该企业拟以月生产效益均值为标准对甲乙两个工厂的工人进行考察，并对生产效益相对较好的工厂工人进行奖励，对生产效益较差的工厂工人进行技能培训，请依据抽测结果给出决策方案.20. （12 分）如图，在四面体48CD中，= "BC = CD = BD = 2,二面角 A BQC 是直二而 角，O为3。的中点，点尸为线段8c上一点，且 OPLBC.（1）求证：8C_L平面AOP；（2）求平面AO尸与平面4CQ所成锐二面角的平面角 的余弦值.21. （12 分）已知g（x） = （x +

10、 l）ln（x+l）（1）讨论/（X）的单调性；（2）若函数/（x） = /（x）-g（x）在定义域上单调递增，求实数。的取值范围.22. （12 分）2,2已知A（-2, V2）, 6（1,0）,椭圆。：+二=1（。>0）经过点人且焦距为4a 夕（1）求椭圆。的方程：（2）过椭圆C的右焦点的直线L与椭圆。交于M,N两点, 求|丽+丽的最小值；（3）右图是椭圆C旋转一定角度的图形，请写出一种尺规作图方案以确定其对称中心的位置， 并在答卷的图中画出来，（不必说明理由）.2021届六校第三次联考数学试题答案一、单项选择题：l.A 2.B3. C 4.D5.A6.D7.B8. A二、多项选择题

11、：9.ACD 10.AC 11.ACD 12 ABD三、填空题13. E14 J'(x) = M(2-W)等15.目也 16. * 或担83332x(2-幻，0 < x < 2, 一2x(2 + x)-2<x<0.部分详解： 14 f(x) = 2忖(2凶)(2 < x < 2),或 /(%) = < 或/(x) = J4忖(2-同)其中之一均可.16 .答：或33有两种情况当AB = AF1时，如左图，医却=叫A周=2mM回=2 +14用=2 + 2m 丁卜耳=卜"| = 2。= m /. |/7jB| = 2m,或用=3mijj2

12、 +4(,-4/ 4/ +4,二9/n2cosZfJF.B + cos/G 居 A = 0 =+= 04c？8c，当 AB = BFi时,如右图，后却=m,AF2 = 2见比却= 2a+mAF = 2a+2mvAB =怛用=> a = m ：. FtB = 3m.AF. = 4m/L.n "L. 八 t/2 +4c2-9a14r+4 3一 16/ 八cosZ?.F,B + cosZA F,A = 0=>+= 0】 -4caSeac2 7c V21:.-=. e =3a3四、解答题17 .详解:方案一:选 = 2a2”是等差数列，其前项和为S”，设其公差为d = S = 1

13、, /. an = a + (- 1)4 = 1 + (- 1)",. a4 = 2a21 + 34 = 2(1 + d) /. d = 1 an = n Sn = n(n +1)4分2;等比数列也J的前项和为T“，设其公比为。v7； = 2S = 2, S3=T2l :.b=T= 29T2 =b1 +b2 =S3=6:.b2=4q =a=2" = AM"" = 2 T =如一"=2n+, - 28分A-qT5<2Sk<Tb26-2<k(k + )<2J-20 62vA(A + l)<126, k -4 = 8,9

14、,10所以存在正整数&使2020+7； <2021,攵=8,9,10io分方案二：选"一仇=4.各项为正的等比数列"的前项和为了”，设其公比为d”>00>0.7； = 23 = 2 .二伪=(=2 :.bn = bxqn-x = 2dl.v /?3 -Z?2 = 4 a 2q- - 2q = 4 :.q = 2, q = - (舍去负的)bn = 2H, 7；=徨(24 分i-q.”是等差数列，前项和为S“，设其公差为d.q = S1 = 1, /. an = a + ( 一)d = 1 + ( 一)dS3=T2 S3 = % + a2 + % =

15、 3 + 3" = A + a=6 /. d = 1a” = S” =，( +1)8 分乙7； K2S* <7； =62攵(攵+ 1)<126, AeN* =攵=8,9,10所以存在整数k使2020 KSa+7； <2021 ,攵=8,9010分方案三：选3工=6.各项为正的等比数列，的前项和为了”，设其公比为。也>0国>0.7 = 2S = 2 二4=7 = 2 /. bn =仇 = 2(广',=4+。2+0 =6二2 + 2q + 2q2 =6,q=1, q =-2 (舍去负的)-， 2=2, Tn = nb = 2n4分%是等差数列，前项和

16、为S“，设其公差为d./. q = Si = 1, /. an = % + ( - 1)" = 1 + ( - 1)4S3=T2 S3 = 6 + 42 + % = 3 + 3d =b+b2 = 4；.d =；an = " (/7 + 2)/. Sn = n(n + 5)8 分367； W2Sk<7； ol0wk(k + 5)W12o30"(k + 5)W36, f(k) = k(k + 5),k e N*是单调递增的.且；/(3) = 24J(4) = 36/M = 4.所以存在唯一的正整数k =4使< 25k k 110分18详解口)已知 a =

17、y/3csin B + bcosC ,用正弦定理 =2R,得:2分sin A sin B sinCsin A = V3 sin Csin B + sin BcosC3分: sin A = sin(- A)= sin(B + C)4分=sin BcosC + cosBsin C 5分VJsinBsinC = cosBsinC, SABO , A,B,C e (0,;r),sinC H 0 73 sin B = cosB tan B 、' a B = 6分36(2)在MCD中用余弦定理得 CD2 =BC2+BD2+2BC BD cosB8分/ AD = 2BD = 2,CD = /i, 7

18、 = 8C? +1 - 2BC cos-9 分6/. BC- -出 BC-6 = 0v BC>0 BC = 2、行10 分又 AB = AQ+£)B = 3S18c. = BC - AB -sin B11分2=x2a/3 x3xsin = -12分26219 .详解：(工)根据所给甲工厂频率分布直方图可知，生产能力总分8090的频率为0.02x10=0.2,生产能力总分90100的频率为0015x10=015,将测评生产能力总分落入各组频率视为概率，则从该工厂随机选取一名工人其生产能力总分超过80分概率是0.2+0.15=0.35,即他是生产能手的概率为0.35.3分(2)据甲

19、厂频率分布直方图可知甲工厂工人在各组相应的频率如下表生产能力总分（分）0,60)60,70)70,80)80,90)90,100频率0.10.250.30.20.155分随机从甲工厂中选取1名工人.用X表示其月生产效益.则X的分布列：X阮；1000015000200002500030000概率0.10.250.30.20.156分所以X的数学期望值E(X)二 10000x0.1+15000x0.25+20000x0.3+25000x0.2+30000x0.15=20250(元)8分(3)由(2)知甲工厂工人月生产效益均值即数学期望E(X)=20250(元) 根据频率分布直方图知乙工厂工人生产能

20、力总分频率分布表：由生产能力总分(分)0.60)60J0)皿80)80,90)90,100频率0.040.20.40.240.12此可得乙工厂工人生产效益Y的分布列：丫阮)1000015000200002500030000所概率0.040.20.40.240.12以乙工厂工人月生产效益均值E(Y)二10000x004+15000x0.2+20000x0.4+25000x0.24+30000x0.12=21000 (元)10分因为E(Y)>E(X),所以推断乙工厂工人月均生产效益比甲的好， 所以应对乙工厂工人进行奖励，对甲工厂工人进行技能培训12分20 .详解：(1)证明：.A8 = 8O

21、,。为 5。的中点.A0_L8。1 分又因为直二面角A-BD-C即平面平面5CD,平面ABDC平面BCD= BDAO_L平面8。2分*.e BCu 2面BCD. AO1,3C3分 又因 OP_L 8copnao =。,。尸 u 平面 4OP,AOu 平面 40P, .8。，平面八。尸(2)连接。C= A3 = AO = &, 3。=。= 3。= 2,。为 8。的中点CO _L 3D A O _L 3。.由 A。_L 平面 BCD:. AOI CO 可以分别以。4,。,。为1轴、y轴、z轴建立空间直角坐标 系,如图。6分又= AB = AD =短,BC = CD = BD = 2 :.A

22、O = OB = OD=、OC = 0: 0(0,00), A(l,0,0), B(0,-l,0), D(0,l,0),C(0,0,73)7分由可知BC_L平面AOP.就为平面AOP的一个法向量，丽=(0,1,途).8分一7 LAD |T-AD = O设平面AC。的一个法向量为 = (x,y,z),则彳一 一 9分n VAC n -AC = 0X5 = (-1,1,0), AC = (-1,0, V3) ：.X+，二 ° ，可取 3 =V3,l)10 分一 x +，3z =。设平面AOP与平面4CD所成锐二面角的平面角为6,则cos。= cos< BC,n> =BCn前1

23、1分12分|Ox + lxV3 + V3xl|、国+川可xj+一21.详解: rW = ex+a. xeR.尸在R上单调递增.当心0/0)>0, /*)在(8,y)上单调递增,当。<0时，/，(x) = Oox = -a + ln(一。)，/' (x) v 0 o x v -a + ln(-a); /' (x) > 0 o x > -a + ln(-a)；./。)在(-8,- + 111(-4)上单调递减；在(-a + In(-a),*o)上单调递增.3分(2)/(x) = eX+"+ar-(x + l)ln(x + l)定义域是(T,+s)；

24、函数F(x)在定义域上单调递增的充要条件是Fx) >0 (x> -1)恒成立4分 法一：/. F*(x) =-ln(x +1)-1 > 0 (x>-l)恒成立 /.,(0) = +6/-1>0令t(x = / + x -1,则r (幻=" +1 > 0.1(X)在R单调递增，r(0) = 0,Z+6/-l = r(tz)>0. a NO7分当。之0时，记G(x)=尸'(x),G'(x) =-一 = h(x)yx >-1x + 1/(x)=4+厂二 > 0G，(x)在(一1,+8)上单调递增(x + 1)-当X 1时

25、G'(x) > -O0; 当X+8时G'(x) +S；存在唯一口枇)使G'(x。)=*一一! = 0,8分4 + 1事实上，取玉=-1 +二， evt7>0.0< <h/.-l<x <0.exa <e = en eaM+l.G'(x1) = G'(-1+-J7)<0又G，(0) = "lN0.存在唯一叫 £ -1 + ,0，使G(%) = 0, - e 一G' (a0 ) = 0 o e %+“ = !, + a = - In (% + 1)X。+1当一 1 v X v X。,

26、G<x) < G'(xo) = O;当X > X。，G' (x) > G'(x0) = 0;.60)在(-1,%)单调递减，在(%,一)单调递增.1n =G(X)mm=G(%)1 0分综上=e"-" + a - Iii(x0 + 1)-1 = ! + t7 + (x0 + 67)-1 % + l=! + Go +1) - 2 + 2a N 2 ；! (x0 +1) - 2 + 2a = 2a 2 0.Xo + 1Vo + 1：.a>0=> Fx)>0可知Q20为所求12分法二：F'(x) = e&qu

27、ot; +«-ln(x + I)-l>0 (x>-l)<=>+(x + a)>x + + ln(x + 1) = * " + ln(x +1) 令T(f) = / + r, Tt) = el+> 0,.丁在R上单调递增/ T(x+a)>T(ln(x +1) /. x + a > ln(x + l)恒成立a > S(x) = ln(x + l) - x ：. a > S(x)max1一 rS'(x) =l = (x>-l)x+x+1/.-1<X< 0 时 S'(x) > 0;

28、X > 0 时,S'(x) < 0/. S *)在(-1,0)上单调递增，田0,+s)上单调递减(0) = 0a>0法三：先证明心) = e*-1-1之0，证明如下： /?'(x) = eI 1. x = 0时(x) = 0;x v 0时7?'(x) < 0;x> 0时力'(x) > 0;.-.X < 0时加幻单调递减x > 0时"(幻单调递增力 Wmin ="=。/*) N 0*)min = 0ex >x + .x + > OJhf In ex 2 ln(x + l)即x-ln(x

29、 + l) 2 0.,.若4 > 0,则Fx = a"" + a ln(x +1) -1 > (x + « +1) + « - In(x +1)-1 =x-ln(x + l) + 2a > 2a N0(x> -1)恒成立若dVO,贝肥° vl.,/(0) = /+a lnl-l=，-l + av0.当且仅当a > 0时尸'(x) 2 0恒成立22.详解：(1)依条件知，椭圆C的焦点在“轴上，长半轴为。，短半轴为方，且焦距2c = 4/.c = 2,椭圆。的两焦点分别为耳(一2,0),乙(2,0).:椭圆C经

30、过点A/. 24 =闺川 + 因川=J+ +a/(-2-2)2+(V2-O)2 =472./.a = 2V2,:.b =cr -c，= 2, %2 y2 fFfi 11 C白勺)i小王xt£ ,、 + z- 1*”384（2）法一：2BP ./分设MCwJ,N&,），2），线段MN的中点为尸（%,肾），则瓯+丽= 1当直线L不垂直于x轴时，设直线L的斜率为k,则直线L方程为y = A(x 2),y7 y.k =:，.，2/ =否 +，2%=Ji + 力，一七xf y ,),!" +彳=-4 - %!2- K+x2.+2y2 -力_()x; y； _8484x2-x1I - I184.2% 2)，_ xO6分又中点P（Xo，%）在直线L （即MN）上，所以刈 =攵（-2）,理由如下（不必写出），设O为对称中心，则12分、2-=0b1，右/=告同理G %=告2当直线L垂直于X轴时，L过尸2,此时“（2,应）,N（2,J5）,，（20）也满足上式.啊 + 网巾叫=24-1)2+(%-0)2 = 2 J(x°