7.4-整周跳变的探测与修复

1、7.4 整周跳变的探测与修复 GPS载波相位测量，只能测量载波滞后相位1周以内的小数部分，不能测量载波滞后相位的整周数。其后的载波滞后相位整周数变化值（始后周数），是通过多普勒积分由电子计数器累计读得的。由于GPS信号接收机自身故障或GPS信号意外中断，导致载波锁相环路的短暂失锁，而引起多普勒计数的短暂中断；当载波锁相环路重新锁定后，多普勒计数又重新开始，以致造成载波滞后相位整周数变化值（始后周数）的不连续计数。这种多普勒计数的中断现象，称为整周跳变，简称为周跳（cycle slip）。当GPS载波相位观测值没有发生周跳时，卫星一次通过的载波滞后相位整周数是连续的，各时元（历元）的观测值都会含

2、有一个共同的整周未知数，即时元的整周模糊度，当发生周跳时，其后所有的载波相位观测值都会含有一偏差，该偏差就是中断期间所丢失的整周计数，即周跳后的载波相位观测中含有未知数。所谓周跳的探测就是利用观测的信息来发现周跳。在探测出周跳后，利用观测信息来估计丢失的周数，从而修正周跳后的载波相位观测值，称为周跳的修复。在探测出周跳之后，也可将视为周跳后的整周模糊度而利用平差的原理解求出这个未知参数，这是一个整周模糊度的求解问题。静态定位中，由于接收机静止不动，周跳的探测与修复问题已得到了很好的解决。在动态环境下，由于动态接收机在不断地运动中，周跳的探测与修复比静态定位要困难得多。由于GPS信号接收机能提供

3、多种观测信息，利用这些观测信息本身的相互关系（无需轨道信息），可以对周跳进行探测和修复，目前主要有下列方法。 （1）根据有周跳现象的发生将会破坏载波相位测量的观测值随时间而有规律变化的特性来探测周跳（高次差或多项式拟合法）（2）利用载波相位及其变化率的多项式拟合来探测、修复周跳（多项式拟合法）；（3）利用伪距和载波相位观测值组合来探测、修复周跳（伪距/载波组合法）；（4）利用双频载波相位组合观测值探测、修复周跳（电离层残差法）。7.4.1用高次差或多项式拟合法此种方法是根据有周跳现象的发生将会破坏载波相位测量的观测值随时间而有规律变化的特性来探测的。GPS卫星的径向速度最大可达因而整周计数每秒

4、钟可变化数千周。因此，如果每15s输出一个观测值的话，相邻观测位间的差值可达数万周，那么对于几十周的跳变就不易发现。但如果在相邻的两个观测值间依次求差而求得观测值的一次差的话这些一次差的变化就要小得多。在一次差的基础上再求二次差，三次差、四次差、五次差时其变化就小得更多了。此时就能发现有周跳现象的时段来。四次、五次差已趋近于零。对于稳定度为的接收机时钟，观测间隔为15s，的频率为，由于振荡器的随机误差而给相邻的载波相位造成的影响为24周，所以用求差的方法一般难以探测出只有几周的小周跳。通常也采用曲线拟合的方法进行计算。根据几个相位测量观测位拟台一个n阶多项式：据此多项式来预估下一个观测值并与实

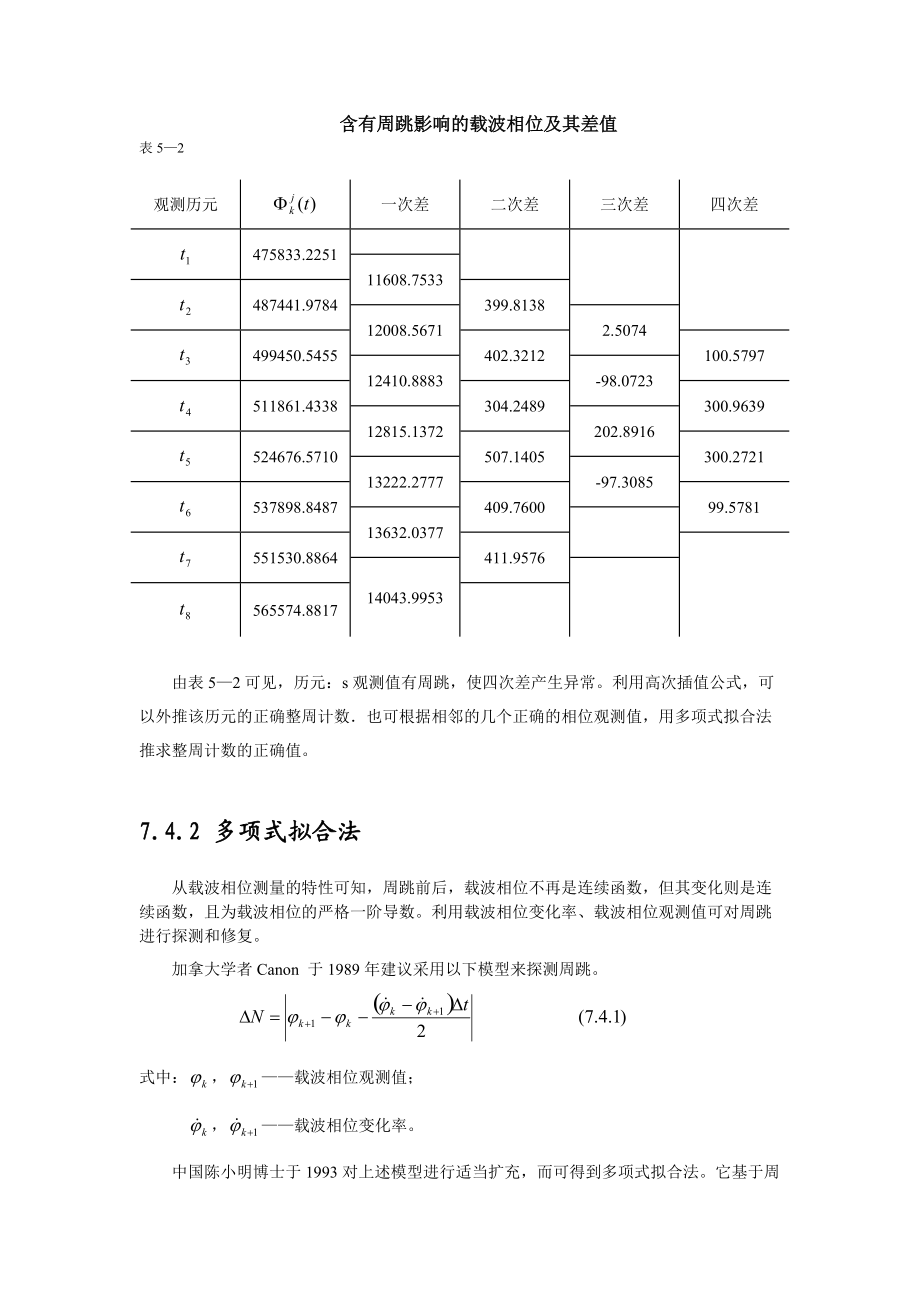
5、测值比较，从而来发现周跳并修正整周计数。表51出了不同历元由测站k对卫星j的相位观测值。因为没有周跳，对不同历元观测值取至4至5次差之后的差值主要是由于振荡器随机误差而引起，具有随机特性。如果在观测过程中产生了周跳现象，高次差的随机特性受到破坏。含有周跳影响的观测值及其差值见表52。载波相位及其差值表51观测历元一次差二次差三次差四次差475833.225111608.7533487441.9784399.813812008.56712.5074499450.5455402.3212-0.579712410.88831.9277511861.4338404.24890.963912815.13

6、722.8916524676.5710407.1405-0.272113222.27772.6195537898.8487409.7600-0.421913632.03772.1976551530.8864411.957614043.9953565574.8817含有周跳影响的载波相位及其差值表52观测历元一次差二次差三次差四次差475833.225111608.7533487441.9784399.813812008.56712.5074499450.5455402.3212100.579712410.8883-98.0723511861.4338304.2489300.963912815.

7、1372202.8916524676.5710507.1405300.272113222.2777-97.3085537898.8487409.760099.578113632.0377551530.8864411.957614043.9953565574.8817由表52可见，历元：s观测值有周跳，使四次差产生异常。利用高次插值公式，可以外推该历元的正确整周计数也可根据相邻的几个正确的相位观测值，用多项式拟合法推求整周计数的正确值。7.4.2 多项式拟合法从载波相位测量的特性可知，周跳前后，载波相位不再是连续函数，但其变化则是连续函数，且为载波相位的严格一阶导数。利用载波相位变化率、载波相位

8、观测值可对周跳进行探测和修复。加拿大学者Canon 于1989年建议采用以下模型来探测周跳。式中：，载波相位观测值； ，载波相位变化率。中国陈小明博士于1993对上述模型进行适当扩充，而可得到多项式拟合法。它基于周跳前后载波相位观测值符合如下多项式模型式中：以周表示的载波相位观测值；周跳数；待求系数。载波相位变化率是载波相位的一阶导数，故载波相位变化率可写为现选取5个时元的载波相位观测值及其变化率：并假设前4个时元的载波相位观测值没有周跳，而用它们来探测和修复第5和时元的载波相位观测值的周跳，依次列如下误差方程：式中：根据最小二乘原理可解得若解得的(为给定限值)，则说明第5个时元的载波相位观测

9、值存在周跳，其周跳估值为。这种方法假定孜给定区间内载波相位变化率为匀加速变化，在实际动态定位中，若目标动态变化较大，则会产生较大的模型误差。现据1996年3月18日在海南省海口市所作的机载GPS测量成果，对上述多项式拟合进行解算实践。该次机载GPS动态载波相位测量采用1s数据采样率（更新率），依次用多项式拟合法探测25号卫星L1载波相位测量的周跳；图7.4.1、图7.4.2、图7.4.3分别表示飞机处于静止待飞、常规直线飞行和加速起飞段的周跳探测结果（数据本身没有周跳）。图7.4.2、图7.4.3中黑线为飞机速度。从图7.4.1可见，对于GPS静态数据，多形式拟合法所得到的均小于0.1周，故可

10、探测出GPS静态定位的所有周跳。图7.4.2的结果表明，当载体作近似匀速直线运动时，多项式拟合法可以探测出大于2周德周跳。图7.4.3的结果表明，由于飞机加速起飞时，特别是离地后，动态变化不稳定，计算值噪声较大，但对于大部分时元的计算小于2周，个别时元虽然大于2周，但小于5周。因而可选取为判断是否有周跳的标准。该方法的优点在于可分别对L1及L2非残差载波相位观测值或双频组合观测值进行周跳探测。但该方法需用到载波相位变化率观测量，而不适用于不能提供载波相位变化率观测值的GPS信号接收机。7.4.3 电离层残差法1989年美国学者Goad提出用双频载波相位测量的电离层残差，探测和修复周跳。称之为电

11、离层残差法，它主要考察不同时元间电离层残差的变化。若不考虑量测噪声和多路径效应，同一时元的双频载波相位测量之差则为将上式两端同除以，则有式中：表示用L1波长的双频载波相位测量电离层延迟的差值，称之为电离层残差。若不存在周跳，时元之间的之差为为时元间电离层残差的变化值。当电离层比较稳定、采样间隔较短（几秒钟），电离层延迟的变化为亚厘米级。图7.4.47.4.7均为在海南省所作的机载GPS动态载波相位测量成果，其数据采样率是一秒钟，且没有发生载波相位测量的整周跳变；图7.4.4和图7.4.6分别是地面基准接收机和机载GPS信号接收机观测PRN29号卫星的电离层残差数据（用L1波长表示，单位为周），

12、图中虚线为卫星的天顶距。图7.4.5和图7.4.7分别是地面基准接收机和机载GPS信号接收机接收观测PRN29号卫星的时元间电离层残差的变化。由图7.4.5可知，对于静态观测的GPS信号接收机时元间电离层残差变化较小，其值均小于0.005周。而图7.4.7表明，对于机载GPS信号接收机，由于多路径效应和测量误差的影响，电离层残差的变化较大，但其都小于0.05周。因而在电离层较稳定时，短时间内载波相位测量电离层残差的变化很小。若相邻两历元间电离层残差发生突变，则说明L1或L2的载波相位观测值可能存在周跳。若设L1，L2的周跳分别为，则有此时，是L1，L2周跳的线性组合。显然，如果L1，L2得周跳

13、使等于或接近于零，从而使时元间电离层残差观测值的变化很小，则用该法无法探测出周跳；亦即，当时，有；此外，当，；，。，。，时，均小于周，特别是当，时，仅为0.0167周，几乎和量测噪声相当（见表7.4.1）。根据上述机载GPS测量成果，选取周为探测周跳的标准，对于大部分周跳均可探测出来。但对一些特殊的周跳组合，如，；，等，则难以探测出周跳。尽管如此，电离层残差法仍然是一种极好的双频周跳探测方法。若能联合应用其他周跳探测方法（如多项式拟合法），将周跳修复至7周以内，电离层残差法，则可正确探测出所有周跳。7.4.4 伪距/载相组合法从GPS卫星测量误差特性可知，除电离层延迟、多路径效应、量测误差之外

14、，其他误差源对伪距和载波相位测量的影响是相同的，故可用伪距和载波相位观测值的组合来探测和修复周跳。单频伪距和载波相位测量的观测方程可表述如下：式中：伪距观测值；载波相位观测值；载波波长；载波相位整周模糊度；，分别为伪距和载波相位测量的电离层效应偏差；，分别为伪距和载波相位测量的多路径效应偏差；，分别为伪距和载波相位的量测噪声。将式（7.4.10）和式（7.4.11）相减可以得到：将式（7.4.12）在时元间相减，由于时元间电离层延迟和多路径效应变化较小时，可以得到周跳的估值：式（7.4.13）可用于单频、非差数据。其估计精度取决于电离层延迟和多路径效应在时元之间的变化，以及伪距和载波相位测量的

15、量测噪声、载波波长的大小。在相同的观测条件下，波长越长，则对周跳的估计越精确。基于上述思想中国韩绍伟博士于1995年提出利用双频组合观测值来探测和修复周跳的方法（此处表示其测距等效波长为86.2cm，表示其测距等效波长为1465.3cm）。每时元双频组合观测值的整周模糊度可用下式来估计：式中： 式（7.4.14）中的可选择为L1或L2的伪距或，也可选择，的平均值，根据不同接收机类型以及可用的伪距观测值，应选择量测噪声较小的伪距观测值作为代入式中计算。若精确已知式（7.4.14）中的电离层延迟，则波长越长，确定精度越高。每一时元的均可用（7.4.14）来估计，当时元间电离层延迟等变化较小时，时元

16、间周跳可用下式估计。对于分别有根据，的定义有以下关系：如果为奇数为奇数；如果为偶数为偶数。这一奇偶关系表明：当其中一个整周模糊度确定后，则另一个的等效波长变为原波长的两倍，因而更容易求解，对于周跳也存在同样的关系：当为奇数为奇数；当为偶数为偶数。显然如果求得则的确定变得更容易，反之亦然。若确定的周跳后，则周跳可用下式确定：图7.4.8图7.4.11分别为一次机载GPS动态定位中周跳探测的结果（GPS信号接收机为Trimble 4000SSE，数据采样率为1s，卫星号PRN25，无周跳），从图7.4.8和图7.4.10可见，无论是对静态GPS信号接收机，还是对机载GPS信号接收机，的噪声不到0.

17、25周，因此，除外所有的周跳都可用来探测到，从图7.4.9和图7.4.11可知；对于静态GPS信号接收机，不难确定到2周左右的水平。若设真实跳周数分别、，且，的估值分别为，则有故知，从式（7.4.18）和式（7.4.19）可以得到3组和的估值，亦即。对于和分别为9和7的整数倍，且估计精确度为2周时周跳无法探测。如果进一步提高伪距观测量精度，使能确定到一周以内的水平，则根据前述奇偶关系，可以唯一确定的周跳。综上所述，上列3种方法都可用于单站星非差观测值（图7.4.1图7.4.11中均采用非差观测值）的周跳探测和修复，且可用于在预处理阶段的周跳探测和修复。多项式拟合法主要用于探测L1和L2的周跳，并可将L1的周跳修复到5周的水平。当动态较稳定时，可修复到2周的水平。对于GPS静态测量数据，则可完全修复周跳。电离层残差法，是探测GP