画法几何及机械制图答案ppt课件_第1页
画法几何及机械制图答案ppt课件_第2页
画法几何及机械制图答案ppt课件_第3页
画法几何及机械制图答案ppt课件_第4页
画法几何及机械制图答案ppt课件_第5页
已阅读5页，还剩14页未读， 继续免费阅读

下载本文档

版权说明：本文档由用户提供并上传，收益归属内容提供方，若内容存在侵权，请进行举报或认领

文档简介

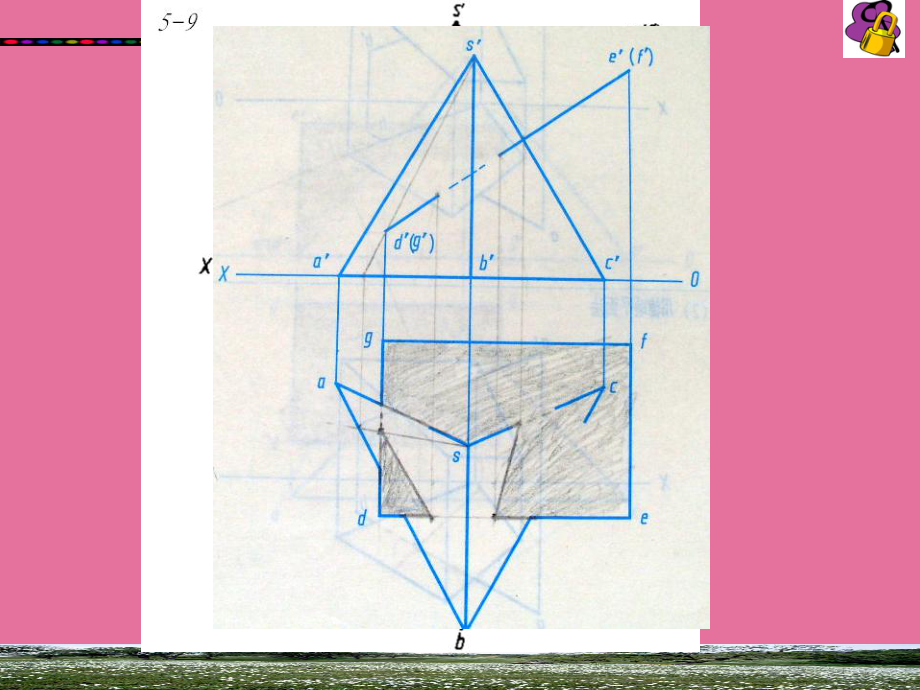
1、习题集 解题过程：1.利用ab/ef，求得b2.衔接ad,在EFG面内作其平行线3.H面内，利用平行求得d点4.利用平行求得c点。 解题终了习题集 习题集 习题集 方法：方法：A点与点与X轴组成一个平面，求轴组成一个平面，求BC与该平面的交点。与该平面的交点。习题集 习题集 习题集 习题集 方法二：方法二：1.求平面求平面ABC与与DEF交线交线2.过过A点作交线的平行线点作交线的平行线AK3. AK即为所求。即为所求。方法三：换面线方法三：换面线1.一次换面将平面一次换面将平面DEF变成线变成线2.过过A点作积聚线的平行线，与点作积聚线的平行线，与BC交于交于K点点3. AK即为所求。即为所

2、求。方法一：方法一：1.过过A点作平面与点作平面与DEF平行平行2.求直线求直线BC与平面的交点与平面的交点K3.衔接衔接AK，即为所求。，即为所求。习题集 习题集 方法二：换面法方法二：换面法1.一次换面将线一次换面将线BD换成实形换成实形2.过中点作过中点作 BD的垂线，与的垂线，与EF交点即为交点即为A3.利用平行关系可得利用平行关系可得C点。点。方法一：方法一：1.过过BD中点作平面与中点作平面与BD垂直垂直2.求直线求直线EF与平面的交点，即为与平面的交点，即为A点点3.利用平行关系可得利用平行关系可得C点。点。习题集 方法一：方法一：1.过过B点点(或或A点点)作平面与作平面与AB

3、垂直垂直2.利用平行可得利用平行可得C点，点，C在平面内在平面内3.利用平行关系可得利用平行关系可得D点。点。方法二：换面法方法二：换面法1.对对AB或或AD一次换面成实形一次换面成实形2.利用垂直可求出利用垂直可求出D点点3.利用平行关系可得利用平行关系可得C点。点。习题集 方法二：换面法方法二：换面法1.一次换面将一次换面将LMN平面换成积聚线平面换成积聚线2.过过A作积聚线平行线，与作积聚线平行线，与FG交点即为交点即为B点点3.其它同法一其它同法一习题集 习题集 方法一：方法一：1.求求AB与平面与平面CDE交点交点K2.对对AB一次换面，过一次换面，过K点作点作AB垂线垂线FG3. FG即为所求。即为所求。方法二：方法二：1.求求AB与平面与平面CDE交点交点K2. 过过K点作点作AB垂面，求垂面与垂面，求垂面与CDE交交线线3. 过过K点作交线平行线，即为所求。点作交线平行线，即为所求。习题集 习题集 方法：换面法方法：换面法1.对对MN二次换面，平面积聚成线二次换面，平面积聚成线2.求求DNC的角平分线，与的角平分线，与AB必有交点必有交点3. 交点交点K即为所求。即为所求。习题集 方法：换面法方法：换面法1.对直线对直线AB二次换面，积聚成点二次换面，积聚成点2.作间隔积聚点作间隔积聚

人人文库> 全部分类> 毕业设计 > 任务书类

温馨提示

  • 1. 本站所有资源如无特殊说明，都需要本地电脑安装OFFICE2007和PDF阅读器。图纸软件为CAD,CAXA,PROE,UG,SolidWorks等.压缩文件请下载最新的WinRAR软件解压。
  • 2. 本站的文档不包含任何第三方提供的附件图纸等，如果需要附件，请联系上传者。文件的所有权益归上传用户所有。
  • 3. 本站RAR压缩包中若带图纸，网页内容里面会有图纸预览，若没有图纸预览就没有图纸。
  • 4. 未经权益所有人同意不得将文件中的内容挪作商业或盈利用途。
  • 5. 人人文库网仅提供信息存储空间，仅对用户上传内容的表现方式做保护处理，对用户上传分享的文档内容本身不做任何修改或编辑，并不能对任何下载内容负责。
  • 6. 下载文件中如有侵权或不适当内容，请与我们联系，我们立即纠正。
  • 7. 本站不保证下载资源的准确性、安全性和完整性, 同时也不承担用户因使用这些下载资源对自己和他人造成任何形式的伤害或损失。

最新文档

评论

0/150

提交评论