数据结构ch6树与二叉树

1、1第第1章章 绪论绪论第第2章章 线性表线性表第第3章章 栈和队列栈和队列 第第4章章 串串第第5章章 数组和广义表数组和广义表第第6 6章章 树和二叉树树和二叉树 第第7章章 图图第第9章章 查找查找第第10章章 排序排序目目 录录2第第6 6章章 树和二叉树树和二叉树（tree & binary tree）6.1 树的基本概念树的基本概念6.2 二叉树二叉树6.3 遍历二叉树和线索二叉树遍历二叉树和线索二叉树6.4 树和森林树和森林6.5 赫夫曼树及其应用赫夫曼树及其应用特点：特点：非线性结构，一个直接前驱，但可能有多个非线性结构，一个直接前驱，但可能有多个直接后继。直接后继。（一

2、对多，或称（一对多，或称1:n1:n）36.16.1 树的基本概念6.1.1 树的定义树的定义6.1.2 若干术语若干术语6.1.3 逻辑结构逻辑结构6.1.4 存储结构存储结构6.1.5 树的运算树的运算4注注1 1：过去许多书籍中都定义树为过去许多书籍中都定义树为n1，曾经有，曾经有“空树不是空树不是树树”的说法，但现在树的定义已修改。的说法，但现在树的定义已修改。注注2：树的定义具有树的定义具有递归性递归性，即，即“树中还有树树中还有树”。由一个或多个由一个或多个( (n0n0) )结点组成的有限集合结点组成的有限集合t t，有且仅有，有且仅有一一个结点称为根个结点称为根（rootroo

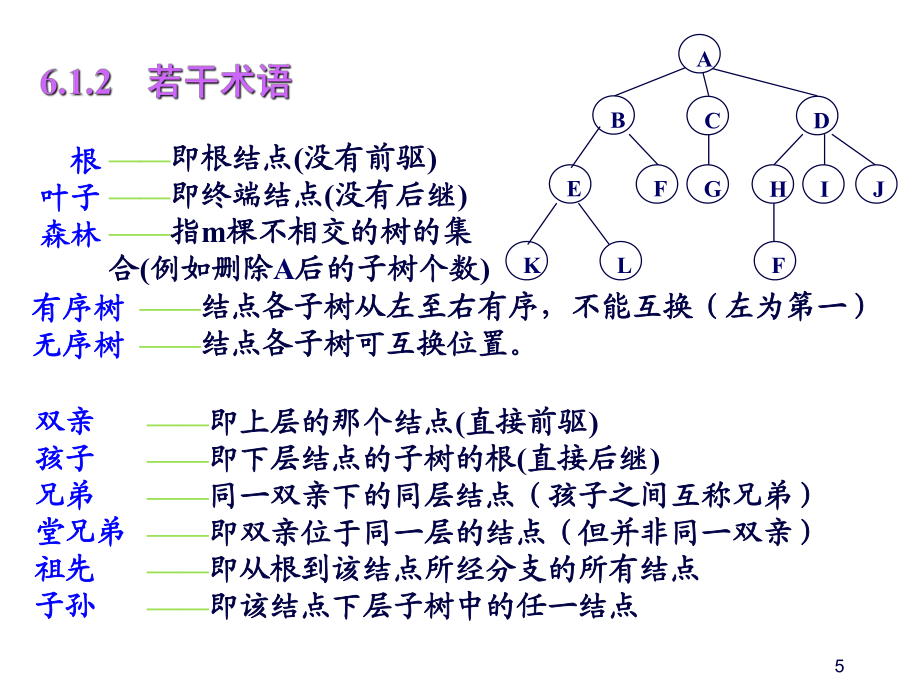
3、t），），当当n1n1时，其余的结点分为时，其余的结点分为m m(m0)(m0)个个互不相交的互不相交的有限集合有限集合t1,t2t1,t2，tmtm。每个集合本身又是棵树，。每个集合本身又是棵树，被称作这个根的被称作这个根的子树子树 。5即上层的那个结点即上层的那个结点(直接前驱直接前驱)即下层结点的子树的根即下层结点的子树的根(直接后继直接后继)同一双亲下的同层结点（孩子之间互称兄弟）同一双亲下的同层结点（孩子之间互称兄弟）即双亲位于同一层的结点（但并非同一双亲）即双亲位于同一层的结点（但并非同一双亲）即从根到该结点所经分支的所有结点即从根到该结点所经分支的所有结点即该结点下层子树中的任一

4、结点即该结点下层子树中的任一结点abcgeidhfjflk 根根 叶子叶子 森林森林有序树有序树无序树无序树即根结点即根结点(没有前驱没有前驱)即终端结点即终端结点(没有后继没有后继)指指m棵不相交的树的集棵不相交的树的集合合(例如删除例如删除a后的子树个数后的子树个数)双亲双亲孩子孩子兄弟兄弟堂兄弟堂兄弟祖先祖先子孙子孙结点各子树从左至右有序，不能互换（左为第一）结点各子树从左至右有序，不能互换（左为第一）结点各子树可互换位置。结点各子树可互换位置。6即树的数据元素即树的数据元素结点挂接的子树数结点挂接的子树数结点结点结点的度结点的度结点的层次结点的层次终端结点终端结点分支结点分支结点树的度

5、树的度树的深度树的深度(或高度或高度)abcgeidhfjflk从根到该结点的层数（根结点算第一层）从根到该结点的层数（根结点算第一层）即度为即度为0的结点，即叶子的结点，即叶子即度不为即度不为0的结点（也称为内部结点）的结点（也称为内部结点）所有结点度中的最大值（所有结点度中的最大值（max各结点的度各结点的度）指所有结点中最大的层数（指所有结点中最大的层数（max各结点的层次各结点的层次）问：问：右上图中的结点数右上图中的结点数 ；树的度；树的度 ；树的深度；树的深度13133 34 4（有几个直接后继就是几度，亦称（有几个直接后继就是几度，亦称“次数次数”）7树的抽象数据类型定义树的抽象

6、数据类型定义（见教材（见教材p118-119p118-119）adt treeadt tree数据对象数据对象d:d:数据关系数据关系r:r:基本操作基本操作 p p：adt treeadt treed是具有相同特性的数据元素的集合。是具有相同特性的数据元素的集合。若若d为空集，则称为空树；为空集，则称为空树；/允许允许n=0若若d中仅含一个数据元素，则中仅含一个数据元素，则r为空集；为空集；其他情况下的其他情况下的r存在二元关系：存在二元关系： root 唯一唯一 /关于根的说明关于根的说明 djdk= /关于子树不相交的说明关于子树不相交的说明 /关于数据元素的说明关于数据元素的说明 /至

7、少有至少有15个，如求树深，求某结点的双亲个，如求树深，求某结点的双亲8一对多（一对多（1:n1:n），），有多个直接后继（如家谱有多个直接后继（如家谱树、目录树等等），但只有一个根结点，树、目录树等等），但只有一个根结点，且且子树之间互不相交。子树之间互不相交。 讨论讨论1：树是非线性结构，该怎样存储？树是非线性结构，该怎样存储？特点：特点：仍然有顺序存储、链式存储等方式。仍然有顺序存储、链式存储等方式。 9讨论讨论3：树的链式存储方案应该怎样制定？树的链式存储方案应该怎样制定？复原困难复原困难可用多重链表：可用多重链表：一个前趋指针，一个前趋指针，n n个后继指针。个后继指针。 细节问题：

8、细节问题： 树中结点的结构类型样式该如何设计？树中结点的结构类型样式该如何设计？ 即应该设计成即应该设计成“等长等长”还是还是“不等长不等长”？ 缺点：缺点： 等长结构太浪费（每个结点的度不一定相同）；等长结构太浪费（每个结点的度不一定相同）； 不等长结构太复杂（要定义好多种结构类型）。不等长结构太复杂（要定义好多种结构类型）。可否规定为：可否规定为： 从上至下、从左至右将树的结点依次存入内存。从上至下、从左至右将树的结点依次存入内存。有重大缺陷：有重大缺陷：不能唯一复原就没有实用价值！不能唯一复原就没有实用价值！讨论讨论2：树的顺序存储方案应该怎样制定？树的顺序存储方案应该怎样制定？data

9、link 1 link 2 .link n.困惑困惑：到底到底应当开多少个链域应当开多少个链域? ?补充：树的补充：树的5种表示法：种表示法：v 图形表示法图形表示法v 嵌套集合表示法嵌套集合表示法v 广义表表示法广义表表示法v 凹入表示法凹入表示法v 左孩子右兄弟表示法左孩子右兄弟表示法意义：把一般的树转化为最简单、最有规律意义：把一般的树转化为最简单、最有规律的二叉树再研究，然后设法从二叉树再转回的二叉树再研究，然后设法从二叉树再转回多叉树。多叉树。11教师教师学生学生其他人员其他人员20052005级级20062006级级20072007级级20082008级级湖北理工学院湖北理工学院计

10、算机系计算机系计算机系计算机系控制系控制系叶子叶子根根子树子树1213( a ( b ( e ( k, l ), f ), c ( g ), d ( h ( m ), i, j ) ) 约定：约定：根根作为由子树森林组成的作为由子树森林组成的表的名字写在表的左边表的名字写在表的左边14又称目录表示法又称目录表示法15data左孩子左孩子 右兄弟右兄弟意义：多叉树转为二叉树！意义：多叉树转为二叉树！16方法：方法：加线加线抹线抹线旋转旋转 abeidfhgc树转二叉树举例：树转二叉树举例：abeidfhgc兄弟相连兄弟相连长兄为父长兄为父孩子靠左孩子靠左17讨论讨论：二叉树怎样还原为树？二叉树怎

11、样还原为树？abeidfhgc要点：要点：逆操作，把逆操作，把所有右孩子变为兄弟所有右孩子变为兄弟！ abdefhgic18要明确：要明确：1. 普通树（即多叉树）若不转化为二叉树，则运算很难实现。普通树（即多叉树）若不转化为二叉树，则运算很难实现。2. 二叉树的运算仍然是插入、删除、修改、查找、排序等，但二叉树的运算仍然是插入、删除、修改、查找、排序等，但这些操作必须建立在这些操作必须建立在对树结点能够对树结点能够“遍历遍历”的基础上！的基础上！本章重点：本章重点：二叉树的表示和实现二叉树的表示和实现196.2 二叉树二叉树为何要重点研究每结点最多只有两个为何要重点研究每结点最多只有两个 “

12、叉叉” 的树？的树？二叉树的结构最简单，规律性最强；二叉树的结构最简单，规律性最强；可以证明，所有树都能转为唯一对应的二叉树，可以证明，所有树都能转为唯一对应的二叉树，不失一般性。不失一般性。6.2.1 二叉树的定义二叉树的定义6.2.2 二叉树的性质二叉树的性质6.2.3 二叉树的存储结构二叉树的存储结构注：二叉树最重要的运算是：遍历！注：二叉树最重要的运算是：遍历！20定义：定义：是是n（n0）个结点的有限集合，由一个根结点以及两）个结点的有限集合，由一个根结点以及两棵互不相交的、分别称为棵互不相交的、分别称为左子树和右子树左子树和右子树的二叉树组成的二叉树组成 。逻辑结构：逻辑结构： 一

13、对二（一对二（1:2） 基本特征基本特征: 每个结点最多只有两棵子树（不存在度大于每个结点最多只有两棵子树（不存在度大于2 2的结点）；的结点）； 左子树和右子树左子树和右子树次序不能颠倒次序不能颠倒。 基本形态：基本形态：一般的树一般的树有几种？有几种？21二叉树的抽象数据类型定义二叉树的抽象数据类型定义（见教材（见教材p p121-122121-122）adt binarytree数据对象数据对象d:数据关系数据关系r:基本操作基本操作 p：adt binarytreed是具有相同特性的数据元素的集合。是具有相同特性的数据元素的集合。若若d=，则，则r= ；若若d，则，则r= h；存在二元

14、关系：；存在二元关系： root 唯一唯一 /关于根的说明关于根的说明 djdk= /关于子树不相交的说明关于子树不相交的说明 /关于数据元素的说明关于数据元素的说明 /关于左子树和右子树的说明关于左子树和右子树的说明 /至少有至少有20个，如返回某结点的左孩子，个，如返回某结点的左孩子，或中序遍历，等等或中序遍历，等等22讨论讨论1 1：第第i i层的结点数最多是多少？层的结点数最多是多少？ （利用二进制性质可轻松求出）（利用二进制性质可轻松求出） 性质性质1:1: 性质性质2:2: 再提问：再提问：第第i i层上至少有层上至少有 个结点？个结点？1 1讨论讨论2 2：深度为深度为k k的二

15、叉树，最多有多少个结点？的二叉树，最多有多少个结点？ （利用二进制性质可轻松求出）（利用二进制性质可轻松求出）233. 3. 深度为深度为9 9的二叉树中至少有的二叉树中至少有 个结点。个结点。 ) )9 9 ) )8 8 ) ) ) )9 91 12.2.深度为的二叉树的结点总数，最多为深度为的二叉树的结点总数，最多为 个。个。 ) )k-1k-1 ) log) log2 2k k ) ) k k ) )k k1. 1. 树中各结点的度的最大值称为树的树中各结点的度的最大值称为树的 。 ) ) 高度高度 ) ) 层次层次 ) ) 深度深度 ) ) 度度dcc课堂练习：课堂练习：24性质性质3

16、: 3: 对于任何一棵二叉树，若对于任何一棵二叉树，若2 2度的结点数有度的结点数有n n2 2个，个，则叶子数（则叶子数（n n0 0）必定为必定为n n2 21 1 （即（即n0=n2+1）二叉树中全部结点数二叉树中全部结点数nn0+n1+n2( (叶子数叶子数1 1度结点数度结点数2 2度结点数度结点数) )二叉树中全部结点数二叉树中全部结点数nb+1 ( ( 总分支数根结点总分支数根结点 ) ) （除根结点外，每个结点必有一个直接前趋，即一个分支）（除根结点外，每个结点必有一个直接前趋，即一个分支）总分支数总分支数b= n1+2n2 (1(1度结点必有度结点必有1 1个直接后继，个直接

17、后继，2 2度结点必有度结点必有2 2个个) )n0+n1+n2= n1+2n2 +1, 即即n0=n2+1讨论：二叉树的叶子数和度为讨论：二叉树的叶子数和度为2 2的结点数之间有关系吗？的结点数之间有关系吗？25完全二叉树：完全二叉树：深度为深度为k 的的、有有n个结点个结点的二叉树，当且仅当其每一个结点都与的二叉树，当且仅当其每一个结点都与深度为深度为k 的满二叉树中编号从的满二叉树中编号从1至至n的结的结点一一对应。点一一对应。aobcgekdjfihnml深度为深度为4 4的满二叉树的满二叉树完全二叉树完全二叉树abcgeidhfj为何要研究为何要研究这两种特殊这两种特殊形式？形式？讨

18、论：满二叉树：讨论：满二叉树：一棵深度为一棵深度为k 且有且有2k -1个结点的二叉树。个结点的二叉树。 （特点：每层都（特点：每层都“充满充满”了结点）了结点）解释：完全二叉树的特点是只有最后一层叶子不满，且解释：完全二叉树的特点是只有最后一层叶子不满，且全部集中在左边。但这其实是全部集中在左边。但这其实是顺序二叉树顺序二叉树的含义。而的含义。而图图论论中的中的“完全二叉树完全二叉树”是指是指n1=0的情况。的情况。满二叉树和完全二叉树有什么区别？满二叉树和完全二叉树有什么区别？答：满二叉树是叶子一个也不少的树，而完全二叉树虽然前答：满二叉树是叶子一个也不少的树，而完全二叉树虽然前k-k-1

19、 1层是满的，但最底层却允许在右边缺少连续若干个结点。满层是满的，但最底层却允许在右边缺少连续若干个结点。满二叉树是完全二叉树的一个特例。二叉树是完全二叉树的一个特例。26证明：证明：根据性质根据性质2 2，深度为深度为k k的二叉树最多只有的二叉树最多只有2 2k k-1-1个结点，且个结点，且完全二叉树的定义是与同深度的满二叉树前面编号相同，即它完全二叉树的定义是与同深度的满二叉树前面编号相同，即它的总结点数的总结点数n n位于位于k k层和层和k-1k-1层满二叉树容量之间，层满二叉树容量之间，即即 2 2k-1k-1-1n2-1n2k k-1 -1 或或2 2k-1k-1n2n2k k

20、三边同时取对数，于是有：三边同时取对数，于是有：k-1logk-1log2 2nk nbdcd l r先序遍历序列：a b d c先序遍历:adbcl d rbl d rl d radcl d r中序遍历序列：b d a c中序遍历:adbc l r dl r dl r dadcl r d后序遍历序列： d b c a后序遍历:b38+*a*/edcb先序遍历结果先序遍历结果+ * * / a b c d e前缀表示法前缀表示法中序遍历结果中序遍历结果a / b * c * d + e中缀表示法中缀表示法后序遍历结果后序遍历结果a b / c * d * e +后缀表示法后缀表示法层次遍历结果

21、层次遍历结果+ * e * d / c a b例例2 2：用二叉树表示算术表达式用二叉树表示算术表达式39ldr(node *root)if(root !=null) ldr(root-lchild); printf(“%d”,root-data); ldr(root-rchild); return(0);lrd (node *root)if(root !=null) lrd(root-lchild); lrd(root-rchild); printf(“%d”,root-data); return(0);typedef struct nodeint data; struct node *lc

22、hild,*rchild； node;node *root; a b cd edlr( node *root )if (root !=null) /非空二叉树非空二叉树 printf(“%d”,root-data); /访问访问d ddlr(root-lchild); /递归遍历左子树递归遍历左子树dlr(root-rchild); /递归遍历右子树递归遍历右子树 return(0); 40对遍历的分析：对遍历的分析：1. 从前面的三种遍历算法可以知道：如果将从前面的三种遍历算法可以知道：如果将print语句抹去，语句抹去，从递归的角度看，这三种算法是完全相同的，或者说这三种从递归的角度看，这

23、三种算法是完全相同的，或者说这三种遍历算法的遍历算法的访问路径是相同的，只是访问结点的时机不同。访问路径是相同的，只是访问结点的时机不同。从虚线的出发点到终点的路径从虚线的出发点到终点的路径上，每个结点经过上，每个结点经过3次次。afedcbg第第1次次经过时访问，是经过时访问，是先序先序遍历遍历第第2次次经过时访问，是经过时访问，是中序中序遍历遍历第第3次次经过时访问，是经过时访问，是后序后序遍历遍历2. 2. 二叉树遍历的时间效率和空间效率二叉树遍历的时间效率和空间效率时间效率时间效率: : /每个结点只访问一次每个结点只访问一次空间效率空间效率: : /栈占用的最大辅助空间栈占用的最大辅

24、助空间精确值：树深为精确值：树深为k k的递归遍历需要的递归遍历需要k+1k+1个辅助单元个辅助单元41例：例：【严题集严题集6.426.42】编写递归算法，计算二叉树编写递归算法，计算二叉树中叶子结点的数目。中叶子结点的数目。 思路：思路：叶子的特点？左右指针均空！叶子的特点？左右指针均空！ 可选用任何一种遍历算法查找叶子，将其统计并打印出来。可选用任何一种遍历算法查找叶子，将其统计并打印出来。 dlr(node *root) /采用先序遍历的递归算法采用先序遍历的递归算法 if ( root!=null ) /非空二叉树条件，等效于非空二叉树条件，等效于 if(rootif(root) )

25、 if(!root-lchild&!root-rchild) /是叶子结点则统计并打印是叶子结点则统计并打印 sum+; printf(%dn,root-data); dlr(root-lchild); /递归遍历左子树，直到叶子处；递归遍历左子树，直到叶子处； dlr(root-rchild); / /递归遍历右子树，直到叶子处；递归遍历右子树，直到叶子处； return(0); 42用空格字符表示用空格字符表示无孩子无孩子或指针或指针为空为空如何如何把二叉树存入电脑内？把二叉树存入电脑内？怎样建树？见教材怎样建树？见教材p131p131例例例：将下面的二叉树以二叉链表形式存入计算机

26、内。例：将下面的二叉树以二叉链表形式存入计算机内。考虑考虑1 1：输入结点时怎样表示：输入结点时怎样表示“无孩子无孩子”？考虑考虑2 2：以何种遍历方式来输入和建树？：以何种遍历方式来输入和建树？将二叉树将二叉树按先序遍历按先序遍历次序输入：次序输入：a b c d e g f (/n)以先序遍历最为合以先序遍历最为合适，让每个结点都适，让每个结点都能及时被连接到位。能及时被连接到位。字符串输完后字符串输完后应当再应当再加一特殊的结束符号加一特殊的结束符号(如如$)，因为，因为 无无法惟一表示结束。法惟一表示结束。43建树算法：建树算法：status createbitree( bitree

27、&t ) /构造二叉树构造二叉树t t scanf(“%c”,&ch); if(ch= )t=null; /立即结束立即结束 else if(!(t=( bitnode*)malloc(sizeof(bitnode)exit(overflow); t-data=ch; /生成根结点生成根结点 createbitree(t-lchild); /构造左子树构造左子树 createbitree(t-rchild); /构造右子树构造右子树 return ok; /createbitreecreatebitree输入序列：输入序列： a b c d e g f 44例：例：已知一棵二叉

28、树的已知一棵二叉树的中序序列中序序列和和后序序列后序序列分别是分别是bdceafhg 和和 decbhgfa，请画出这棵二叉树。，请画出这棵二叉树。分析：分析：由后序遍历特征，根结点必在后序序列尾部由后序遍历特征，根结点必在后序序列尾部（即（即a a）；由中序遍历特征，根结点必在其中间，而且其左部必全部是由中序遍历特征，根结点必在其中间，而且其左部必全部是左子树的子孙左子树的子孙（即（即bdcebdce），），其右部必全部是右子树的子孙其右部必全部是右子树的子孙（即（即fhgfhg）；）；继而，根据后序中的继而，根据后序中的decbdecb子树可确定子树可确定b b为为a a的左孩子，根据的左

29、孩子，根据hgfhgf子串可确定子串可确定f f为为a a的右孩子；以此类推。的右孩子；以此类推。【严题集严题集6.31】 请证明：由一棵二叉树的先序序列和中序序请证明：由一棵二叉树的先序序列和中序序列可唯一确定这棵二叉树。列可唯一确定这棵二叉树。 45已知中序遍历：已知中序遍历：b d c e a f h g已知后序遍历：已知后序遍历：d e c b h g f a（b d c e）（ f h g）a （d c e）bfghcd eabbaccd c e详细说明：详细说明：6.3.2 线索二叉树线索二叉树所以，所以， 空指针数目空指针数目2n(n-1)=n+1个个。证明：证明：因为用二叉链表

30、存储包含因为用二叉链表存储包含n n个结点的二叉树，结点必有个结点的二叉树，结点必有2n个个链域链域（见二叉链表数据类型说明）（见二叉链表数据类型说明）。又因为除根结点外，二叉树中每一个结点又因为除根结点外，二叉树中每一个结点有且仅有一个双亲有且仅有一个双亲，意即每个结点地址占用了双亲的一个直接后继，意即每个结点地址占用了双亲的一个直接后继，n n个结点地址个结点地址共占用了共占用了n-1n-1个双亲的指针域个双亲的指针域。也就是说，只会有。也就是说，只会有n n1 1个结点个结点的链域存放指针。的链域存放指针。threaded binary tree讨论：讨论：用二叉链表法（用二叉链表法（l

31、_child, r_child）存储包含存储包含n个结点个结点的二叉树，结点的指针区域中会有多少个的二叉树，结点的指针区域中会有多少个空空指针？指针？结论：结论：用二叉链表法存储包含用二叉链表法存储包含n n个结点的二叉树，结点的指针区个结点的二叉树，结点的指针区域中会有域中会有n+1n+1个空指针。个空指针。可以用它来可以用它来存放当前结点的直接前驱和后继存放当前结点的直接前驱和后继等线索，以加快查等线索，以加快查找速度。找速度。这就是这就是的意义和用途。的意义和用途。疑问疑问1：二叉树是二叉树是1:2的非线性结构，如何定义其惟一的直接后继？的非线性结构，如何定义其惟一的直接后继？答：答：要

32、遍历之后才能得到，且不同遍历算法得到的后继也不同。要遍历之后才能得到，且不同遍历算法得到的后继也不同。先依遍历规则先依遍历规则把每个结点对应的把每个结点对应的前驱前驱或或后继线索后继线索预存预存起来，这叫做起来，这叫做“线索化线索化”。疑问疑问2：获得这种：获得这种“直接前驱直接前驱”或或“直接后继直接后继”有何意义？有何意义？答：答：从从任一结点任一结点出发都能快速找到其前驱和后继，且出发都能快速找到其前驱和后继，且不必借助堆栈不必借助堆栈疑问疑问3：如何经济的：如何经济的(预先预先)存放这类信息？存放这类信息？答：答：左孩子左孩子/前驱前驱复用，复用，右孩子右孩子/后继后继复用，后者称之为

33、复用，后者称之为线索线索lchildltagdatartag rchild约定约定:当当tag域为域为0时时,表示表示正常正常情况情况;当当tag域为域为1时时,表示表示线索线索情况情况.前驱前驱(后继后继)左左(右右)孩子孩子为识别复用的两种不同信息，特增加两个标志域：为识别复用的两种不同信息，特增加两个标志域：问：问：增加了前驱和后继等线索有什么好处？增加了前驱和后继等线索有什么好处？能方便找出当前结点的前驱和后继，不用能方便找出当前结点的前驱和后继，不用堆栈（递归）也能遍历整个树。堆栈（递归）也能遍历整个树。各各1bit 1bit 疑问疑问4：计算机如何识别是孩子指针还是线索指针？：计算

34、机如何识别是孩子指针还是线索指针？1. 1. 有关线索二叉树的几个术语：有关线索二叉树的几个术语： 线索链表：线索链表： 线线 索：索：线索二叉树：线索二叉树： 线线 索索 化：化：用用含含tag的结点样式所构成的二叉链表的结点样式所构成的二叉链表指向结点前驱和后继的指针指向结点前驱和后继的指针加上线索的二叉树加上线索的二叉树对二叉树以对二叉树以某种次序遍历某种次序遍历使其变为线索使其变为线索二叉树的过程二叉树的过程线索化过程就是在遍历过程中修改空指针的过程：线索化过程就是在遍历过程中修改空指针的过程：将空的将空的l lchildchild改为结点的直接前驱；改为结点的直接前驱；将空的将空的r

35、 rchildchild改为结点的直接后继。改为结点的直接后继。非空指针呢？仍然指向孩子结点非空指针呢？仍然指向孩子结点（称为（称为“正常情况正常情况”）dataageidjhcfbltag0011110101rtag0001010111ageidjhcfb例：例：带了带了两个标志两个标志的某的某先序先序遍历结果如下表所示，遍历结果如下表所示，请画出对应的二叉树。请画出对应的二叉树。altag=1表示表示前驱线索前驱线索rtag=1表示表示后继线索后继线索abcgeidhfroot悬空？悬空？ nilnil悬空？悬空？ nilnil解：解：对该二叉树对该二叉树中序中序遍历的结果为遍历的结果为:

36、 : h, d, i, b, e, a, f, c, g所以添加线索应当按如下路径进行：所以添加线索应当按如下路径进行：为为避免悬空避免悬空态，应增设态，应增设一个头结点一个头结点例例1 1：画出以下二叉树对应的画出以下二叉树对应的中序中序线索二叉树。线索二叉树。2. 2. 线索二叉树的生成线索二叉树的生成线索化线索化线索化过程就是在遍历过线索化过程就是在遍历过程中修改空指针的过程程中修改空指针的过程00a00c00b11e11f11g00d11i11h注：此图中序遍历结果为注：此图中序遍历结果为: : h, d, i, b, e, a, f, c, g0root0对应的中序线索二叉树存储结构

37、如图所示：对应的中序线索二叉树存储结构如图所示：例例2 2：【 2000 2000年计算机系考研题年计算机系考研题】给定如图所示给定如图所示二叉树二叉树t t，请画出与其对应的中序线索二叉树。请画出与其对应的中序线索二叉树。 2825405560330854解解: :因为中序遍历序列是：因为中序遍历序列是：5555 40 25 60 40 25 60 28 28 08 33 08 33 5454对应线索树应当按此规律连线，即对应线索树应当按此规律连线，即在原二叉树中添加虚线。在原二叉树中添加虚线。nilnilnilnilnilnil和和nullnull的值都是的值都是0,0,区区别何在？别何在

38、？ 在在delphidelphi中中nilnil用来标记用来标记空指针空指针，nullnull用来表示用来表示空的空的variantvariant型变量或是型变量或是asciiascii码为码为0 0的字符，比的字符，比如用于标记字符串结束。如用于标记字符串结束。在在c/c+c/c+中定义的宏中定义的宏nullnull不加区别的包括了以上不加区别的包括了以上两种含义。两种含义。可见可见object pascalobject pascal的语的语法要比法要比c/c+c/c+严谨得多。严谨得多。线索二叉树的线索二叉树的生成生成算法算法（递归算法见教材递归算法见教材p134-135p134-135）

39、目的：目的：在遍历二叉树的过程中修改空指针，添加前驱或后继在遍历二叉树的过程中修改空指针，添加前驱或后继的线索，使之成为线索二叉树。的线索，使之成为线索二叉树。为了记下遍历过程中访问结点的先后次序，需要设置两个指针：为了记下遍历过程中访问结点的先后次序，需要设置两个指针：p指针指针当前结点之指针；当前结点之指针；pre指针指针当前结点的前趋结点指针。当前结点的前趋结点指针。设计技巧：设计技巧：依某种顺序依某种顺序遍历二叉树，对每个结点遍历二叉树，对每个结点p，判断其左指判断其左指针是否为空，以及其针是否为空，以及其前驱结点的前驱结点的右指针是否为空。右指针是否为空。每次只修改每次只修改前驱结点

40、的右指针前驱结点的右指针（后继）和（后继）和本结点的左指针本结点的左指针（前（前驱）驱），参见算法，参见算法6.6。若若p-lchildnull, ,则则p-p-ltagltag=1;=1;p-p-lchildlchildpre;pre; /p/p的前驱线索应存的前驱线索应存p p结点的左边结点的左边若若pre-rchildnull, 则则pre-pre-rtagrtag1;1;pre-pre-rchildrchild=p=p; /pre/pre的后继线索应存的后继线索应存prepre结点的右边结点的右边3. 3. 线索二叉树的遍历线索二叉树的遍历（无需堆栈）（无需堆栈）对于线索二叉树的遍历，

41、只要找到序列中的对于线索二叉树的遍历，只要找到序列中的第一个第一个结结点，然后点，然后依次访问结点的后继依次访问结点的后继直到后继为空为止。直到后继为空为止。（因为建立线索时已遍历一次，相当于线性化了！）（因为建立线索时已遍历一次，相当于线性化了！）难点：难点：在线索化二叉树中，并不是每个结点都能直接在线索化二叉树中，并不是每个结点都能直接找到其后继的，找到其后继的，当标志为当标志为0 0时，则需要通过一定运算时，则需要通过一定运算才能找到它的后继。才能找到它的后继。以以中序线索二叉树中序线索二叉树为例：为例：当当rtag=1时，直接后继指针就在其时，直接后继指针就在其rchild域内；域内；

42、当当rtag=0时，直接后继是当前结点时，直接后继是当前结点的结点的结点；请注意中序遍历规则是请注意中序遍历规则是ldr，5 5）当）当rtagrtag=0=0时时（表示有右孩子）（表示有右孩子） ，此时应当从该结点的，此时应当从该结点的右孩子开始右孩子开始(p=p-(p=p-rchildrchild）查找左下角的子孙结点；即查找左下角的子孙结点；即重复重复2）附：附：中序中序线索二叉树遍历步骤线索二叉树遍历步骤 （算法（算法6.56.5）：1）设置一个搜索指针）设置一个搜索指针p；2）先寻找中序遍历之）先寻找中序遍历之首结点首结点（即最左下角结点），（即最左下角结点），方法是：方法是：当当l

43、tagltag=0=0时时（表示有左孩子），（表示有左孩子），p=p-p=p-lchildlchild; ; 直到直到ltagltag=1=1（无左孩子，已到最左下角）无左孩子，已到最左下角）；首先访问首先访问p-datap-data；3）接着进入该结点的右子树，检查）接着进入该结点的右子树，检查rtagrtag 和和p-p-rchildrchild ；4 4） 若该结点的若该结点的rtagrtag=1=1(表示有后继线索表示有后继线索)，则则p=p-p=p-rchildrchild ；访问访问p-datap-data ;并重复并重复4） ，直到后继结点的，直到后继结点的rtagrtag=0=

44、0；有有后继找后继，后继找后继，无后继找无后继找右子树右子树的最左子孙的最左子孙有后继找后继有后继找后继算法流程：算法流程：return ok;return ok;p=t-p=t-lchildlchild; ;p!=tp!=tp-p-ltagltag=0=0p=p-p=p-lchildlchild; ;visit(p-data);visit(p-data);p-p-rtagrtag=1=1&p-&p-rchildrchild!=t!=tp=p-p=p-rchild;visit(prchild;visit(p-data);-data);p=p-p=p-rchildrchild;

45、;y yn ny yn ny yn n先找最左子孙先找最左子孙找到最左子孙找到最左子孙无后继找右子树无后继找右子树的最左子孙的最左子孙6.4 树和森林6.4.1 树和森林与二叉树的转换树和森林与二叉树的转换6.4.2 树和森林的存储方式树和森林的存储方式6.4.3 树和森林的遍历树和森林的遍历58方法：方法：加线加线抹线抹线旋转旋转 abeidfhgcabeidfhgc兄弟相连兄弟相连长兄为父长兄为父孩子靠左孩子靠左6.4.1 6.4.1 树和森林与二叉树的转换树和森林与二叉树的转换回顾回顾1 1：树如何转为二叉树？树如何转为二叉树？左孩子左孩子右右兄弟表示法兄弟表示法59回顾回顾2 2：二叉

46、树怎样还原为树？二叉树怎样还原为树？abeidfhgc要点：要点：逆操作，把逆操作，把所有右孩子变为兄弟所有右孩子变为兄弟！ abdefhgic60法一：法一： 各森林先各自转为二叉树；各森林先各自转为二叉树； 依次连到前一个二叉树的右子树上。依次连到前一个二叉树的右子树上。讨论讨论1 1：森林如何转为二叉树？森林如何转为二叉树？即即f=tf=t1 1, t, t2 2, , ,t,tm m b=root, lb, rb b=root, lb, rb法二：法二：森林直接变兄弟，再转为二叉树森林直接变兄弟，再转为二叉树（参见教材（参见教材p138p138图图6.176.17，两种方法都有转换示意

47、图），两种方法都有转换示意图）法一和法二得到的二叉树是完法一和法二得到的二叉树是完全相同的、惟一的。全相同的、惟一的。61abcdefghjiabcdefghjibcdefghji森林转二叉树举例：森林转二叉树举例：（用法二，森林直接变兄弟，再转为二叉树）（用法二，森林直接变兄弟，再转为二叉树）兄弟相连兄弟相连 长兄为父长兄为父头树为根头树为根 孩子靠左孩子靠左62bcdefghji讨论讨论2 2：二叉树如何还原为森林？二叉树如何还原为森林？要点：要点：把最右边的子树变为森林，其余右子树变为兄弟把最右边的子树变为森林，其余右子树变为兄弟 即即b=root, lb, rb f=tb=root,

48、lb, rb f=t1 1, t, t2 2, , ,t,tm m abcdefghjiefabcdghji636.4.2 6.4.2 树和森林的存储方式树和森林的存储方式树有三种常用存储方式：树有三种常用存储方式：双亲表示法双亲表示法 孩子表示法孩子表示法 孩子孩子兄弟表示法兄弟表示法 nextsiblingdatafirstchild指向左孩子指向左孩子指向右兄弟指向右兄弟问：问：树树二叉树的二叉树的“连线连线抹线抹线旋转旋转” 如何由计算机自动实现如何由计算机自动实现？答：答：用用“左孩子右兄弟左孩子右兄弟”表示法来存储即可。表示法来存储即可。 64abecdfhgbacedfgh例如例

49、如：6566因课时有限，因课时有限， “树和森林树和森林的遍历的遍历”请自学请自学6.4.3 6.4.3 树和森林的遍历树和森林的遍历例如：例如：abdec先根序列：先根序列：后根序列：后根序列：a b c d eb d c e a深度优先遍历深度优先遍历（先根、后根）（先根、后根）广度优先遍历广度优先遍历（层次）（层次）先根遍历先根遍历访问根结点；访问根结点；依次先根遍历根结点依次先根遍历根结点的每棵子树。的每棵子树。后根遍历后根遍历 依次后根遍历根结点的每依次后根遍历根结点的每棵子树；棵子树； 访问根结点。访问根结点。树没有中序遍历（因树没有中序遍历（因子树不分左右）子树不分左右）67讨论

50、：树若采用讨论：树若采用“先转换，后遍历先转换，后遍历”方式，结果是否一样？方式，结果是否一样？abdec先序遍历：先序遍历：后序遍历：后序遍历：中序遍历：中序遍历：d e c b aabdeca b c d eb d c e a1. 树的先根遍历与二叉树的树的先根遍历与二叉树的先序先序遍历相同；遍历相同； 2. 树的树的后根后根遍历相当于二叉树的遍历相当于二叉树的中序中序遍历；遍历；3. 树没有中序遍历，因为子树无左右之分。树没有中序遍历，因为子树无左右之分。结论：结论：树的先根序列：树的先根序列：a b c d e树的后根序列：树的后根序列：b d c e a68先序遍历先序遍历若森林为空

51、，返回；若森林为空，返回；访问森林中第一棵树的根结点；访问森林中第一棵树的根结点；先根遍历第一棵树的根结点的子树森林；先根遍历第一棵树的根结点的子树森林；先根遍历除去第一棵树之后剩余的树构成的森林。先根遍历除去第一棵树之后剩余的树构成的森林。森林的遍历森林的遍历abcdefghji为何有中序？为何有中序？深度优先遍历深度优先遍历（先序、中序）（先序、中序）广度优先遍历广度优先遍历（层次）（层次）中序遍历中序遍历若森林为空，返回；若森林为空，返回；中根遍历森林中第一棵树的根结点的子树森林；中根遍历森林中第一棵树的根结点的子树森林；访问第一棵树的根结点；访问第一棵树的根结点；中根遍历除去第一棵树之

52、后剩余的树构成的森林。中根遍历除去第一棵树之后剩余的树构成的森林。69讨论：讨论：若采用若采用“先转换，后遍历先转换，后遍历”方式，结果是否相同？方式，结果是否相同？例如：例如：先序序列：先序序列：中序序列：中序序列：a b c d e f g h i jb c d a f e h j i g先序序列：先序序列：中序序列：中序序列：a b c d e f g h i jb c d a f e h j i g结论：结论：森林的先序和中序遍历在森林的先序和中序遍历在两种方式下的结果相同。两种方式下的结果相同。706.5 6.5 二叉树的典型应用二叉树的典型应用平衡树平衡树排序树排序树字典树字典树判

53、定树判定树带权树带权树最优树最优树由字符串构成的二叉排序树由字符串构成的二叉排序树特点特点：分支查找树（例如：分支查找树（例如1212个球如何只称个球如何只称3 3次次便分出轻重）便分出轻重）特点特点：路径带权值（例如长度）：路径带权值（例如长度）是带权路径长度最短的树，又称是带权路径长度最短的树，又称 huffmanhuffman树，树，用途之一是通信中的压缩编码。用途之一是通信中的压缩编码。特点特点：所有结点左右子树深度差：所有结点左右子树深度差1 1特点特点：所有结点：所有结点“左小右大左小右大”71lhuffman树概念的引入树概念的引入l最佳判定树最佳判定树等级分数段比例abcde0

54、5960697079 8089 901000.050.150.400.300.10a60a90a80a70eyndyncynbyna70a80a60cynbyndyneyna80a9060a70eadeca80a70a60a90eyndyncynbyna什么是带权树？什么是带权树？abdc7524即叶子带有权值。例如：即叶子带有权值。例如：最优二叉树最优二叉树( (哈夫曼树哈夫曼树) )如果是带权路径长如果是带权路径长度最短的树度最短的树736.6 huffman6.6 huffman树及其应用树及其应用一、一、huffmanhuffman树树二、二、huffmanhuffman编码编码最优二

55、叉树最优二叉树huffmanhuffman树树huffmanhuffman编码编码带权路径带权路径长度最短长度最短的树的树不等长编码不等长编码是通信中是通信中最经典的最经典的压缩编码压缩编码74树的带权路径长树的带权路径长度如何计算？度如何计算？wplwpl = = w wk kl lk k k=1k=1n nabdc7524(a)cdab2457(b)bdac7524(c)经典之例：经典之例：wpl=wpl=wpl=huffman树是树是wpl wpl 最小的树最小的树树中所有叶子结树中所有叶子结点的带权路径长点的带权路径长度之和度之和36463575一、一、 huffmanhuffman树

56、树（最优二叉树）（最优二叉树）路路 径径：路径长度路径长度：树的路径长度树的路径长度：带权路径长度带权路径长度：树的带权路径长度树的带权路径长度：huffmanhuffman树树：由一结点到另一结点间的分支所构成。由一结点到另一结点间的分支所构成。路径上的分支数目。路径上的分支数目。从树根到从树根到每一结点每一结点的路径长度之和。的路径长度之和。结点到根的路径长度与结点上权的乘积（结点到根的路径长度与结点上权的乘积（wplwpl）若干术语：若干术语：debacf g即树中所有即树中所有叶子结点叶子结点的带权路径长度之和的带权路径长度之和带权路径长度最小的树。带权路径长度最小的树。例如：例如：a

57、eae的路径长度的路径长度树长度树长度2 21010huffmanhuffman常译为常译为赫夫曼、霍夫曼、哈夫曼、胡夫曼等赫夫曼、霍夫曼、哈夫曼、胡夫曼等weighted path lengthweighted path length761. 1. 构造构造huffmanhuffman树的基本思想：树的基本思想：设有设有4 4个字符个字符d,i,a,nd,i,a,n，出现的频度分别为，出现的频度分别为7,5,2,47,5,2,4， 怎样编码才能使它们组成的报文在网络中传得最快？怎样编码才能使它们组成的报文在网络中传得最快？法法1 1：等长编码：等长编码（如二进制编码）（如二进制编码）令令d=

58、d=0000，i=i=0101，a=a=1010，n=n=1111，则：，则：wplwpl1 12bit2bit(7(75 52 24 4）3636法法2 2：不等长编码：不等长编码（如（如huffmanhuffman编码）编码）令令d=d=0 0;i=;i=1010,a=,a=110110,n=,n=111111，则：，则：讨论：讨论：huffmanhuffman树有什么用？树有什么用？权值大的结点用短路径，权值小的结点用长路径。权值大的结点用短路径，权值小的结点用长路径。wplwpl最小的树最小的树频度高的信息频度高的信息用短码，低的用短码，低的用长码，传输用长码，传输效率肯定高！效率肯定

59、高！wplwpl2 2= =1 1bitbit7 72 2bitbit5+35+3bitbit(2+4)=(2+4)=3535最小冗余编码、信息高效传输最小冗余编码、信息高效传输77step1step1：在权值集合在权值集合7,5,2,47,5,2,4中，总是合并中，总是合并当前值最小当前值最小的两个权的两个权先介绍先介绍huffmanhuffman树的具体构造步骤：树的具体构造步骤：a. 初始初始方框表示外结点（叶子，字符）方框表示外结点（叶子，字符）圆框表示内结点圆框表示内结点（合并后的权值）（合并后的权值）b. 合并合并2 4c. 合并合并5 6d. 合并合并7 11谁左谁右？若不谁左谁

60、右？若不规定就会不惟一规定就会不惟一78step2step2：d da ai in n1 11 11 10 00 00 0huffmanhuffman编码结果：编码结果：d=d=0 0, i=, i=1010, a=, a=110110, n=, n=111111wpl=1wpl=1bitbit7 72 2bitbit5+35+3bitbit(2+4)=(2+4)=3535（小于等长码的（小于等长码的wpl=36wpl=36）huffmanhuffman编码也称为编码也称为huffmanhuffman树树 与与 huffmanhuffman编码编码 挂钩挂钩792. 2. 构造构造huffmanhuffman树的步骤树的步骤（即（即hu