【2014届高考物理易错题查漏补缺】专题18牛顿运动定律总结解析

1、2014 届高考物理易错题查漏补缺专题 18 牛顿运动定律总结（一）牛顿第一定律（即惯性定律）一切物体总保持匀速直线运动状态或静止状态，直到有外力迫使它改变这种状态为止。（ 1）理解要点：运动是物体的一种属性，物体的运动不需要力来维持。它定性地揭示了运动与力的关系：力是改变物体运动状态的原因，是使物体产生加速度的原因。第一定律是牛顿以伽俐略的理想斜面实验为基础，总结前人的研究成果加以丰富的想象而提出来的；定律成立的条件是物体不受外力，不能用实验直接验证。牛顿第一定律是牛顿第二定律的基础，不能认为它是牛顿第二定律合外力为零时的特例，第一定律定性地给出了力与运动的关系，第二定律定量地给出力与运动的

2、关系。（ 2）惯性：物体保持原来的匀速直线运动状态或静止状态的性质叫做惯性。惯性是物体的固有属性，与物体的受力情况及运动状态无关。质量是物体惯性大小的量度。 由 牛 顿 第 二 定 律 定 义 的 惯 性 质 量 m=F/a 和 由 万 有 引 力 定 律 定 义 的 引 力 质 量mFr 2 / GM 严格相等。惯性不是力，惯性是物体具有的保持匀速直线运动或静止状态的性质、力是物体对物体的作用，惯性和力是两个不同的概念。（二）牛顿第二定律1. 定律内容物体的加速度a 跟物体所受的合外力F合 成正比，跟物体的质量m 成反比。2. 公式： F合 ma理解要点：因果性： F合 是产生加速度a 的原

3、因， 它们同时产生， 同时变化， 同时存在， 同时消失；方向性： a 与 F合 都是矢量，方向严格相同；瞬时性和对应性：a 为某时刻某物体的加速度，F合 是该时刻作用在该物体上的合外力。（三）力的平衡1. 平衡状态指的是静止或匀速直线运动状态。特点：a0 。2. 平衡条件共点力作用下物体的平衡条件是所受合外力为零，即F0 。3. 平衡条件的推论（ 1 ）物体在多个共点力作用下处于平衡状态，则其中的一个力与余下的力的合力等大反向；（ 2）物体在同一平面内的三个不平行的力作用下，处于平衡状态， 这三个力必为共点力；（ 3 ）物体在三个共点力作用下处于平衡状态时，图示这三个力的有向线段必构成闭合三角

4、形。（四）牛顿第三定律两个物体之间的作用力和反作用力总是大小相等，方向相反，作用在一条直线上，公式可写为 FF'。（五）力学基本单位制：kg、m、s （在国际制单位中）1. 作用力与反作用力的二力平衡的区别内容作用力和反作用力二力平衡受力物体作用在两个相互作用的物体上作用在同一物体上依赖关系同时产生，同时消失相互依存，不可无依赖关系，撤除一个、另一个可依单独存在然存在，只是不再平衡叠加性两力作用效果不可抵消，不可叠加，两力运动效果可相互抵消，可叠加，不可求合力可求合力，合力为零；形变效果不能抵消力的性质一定是同性质的力可以是同性质的力也可以不是同性质的力2. 应用牛顿第二定律解题的一般

5、步骤确定研究对象；分析研究对象的受力情况画出受力分析图并找出加速度方向；建立直角坐标系，使尽可能多的力或加速度落在坐标轴上，并将其余分解到两坐标轴上；分别沿x 轴方向和y 轴方向应用牛顿第二定律列出方程；统一单位，计算数值。3. 解决共点力作用下物体的平衡问题思路（ 1）确定研究对象：若是相连接的几个物体处于平衡状态，要注意“整体法”和“隔离法”的综合运用；（ 2）对研究对象受力分析，画好受力图；（ 3）恰当建立正交坐标系，把不在坐标轴上的力分解到坐标轴上。建立正交坐标系的原则是让尽可能多的力落在坐标轴上。（ 4）列平衡方程，求解未知量。4. 求解共点力作用下物体的平衡问题常用的方法（ 1）有

6、不少三力平衡问题，既可从平衡的观点（根据平衡条件建立方程求解）平衡法，也可从力的分解的观点求解分解法。两种方法可视具体问题灵活运用。（ 2）相似三角形法：通过力三角形与几何三角形相似求未知力。对解斜三角形的情况更显优势。（ 3）力三角形图解法，当物体所受的力变化时，通过对几个特殊状态画出力图（在同一图上）对比分析，使动态问题静态化，抽象问题形象化，问题将变得易于分析处理。5. 处理临界问题和极值问题的常用方法涉及临界状态的问题叫临界问题。临界状态常指某种物理现象由量变到质变过渡到另一种物理现象的连接状态，常伴有极值问题出现。如：相互挤压的物体脱离的临界条件是压力减为零；存在摩擦的物体产生相对滑

7、动的临界条件是静摩擦力取最大静摩擦力，弹簧上的弹力由斥力变为拉力的临界条件为弹力为零等。临界问题常伴有特征字眼出现，如“恰好” 、“刚刚”等，找准临界条件与极值条件，是解决临界问题与极值问题的关键。例 1. 如图 1 所示，一细线的一端固定于倾角为 45°的光滑楔形滑块一端拴一质量为 m 的小球。当滑块以 2g 加速度向左运动时，线中拉力A 的顶端 P 处，细线另 T 等于多少？解析： 当小球和斜面接触，但两者之间无压力时，设滑块的加速度为a'此时小球受力如图2，由水平和竖直方向状态可列方程分别为：T cos45T sin 45ma' mg0解得：a'g由滑块

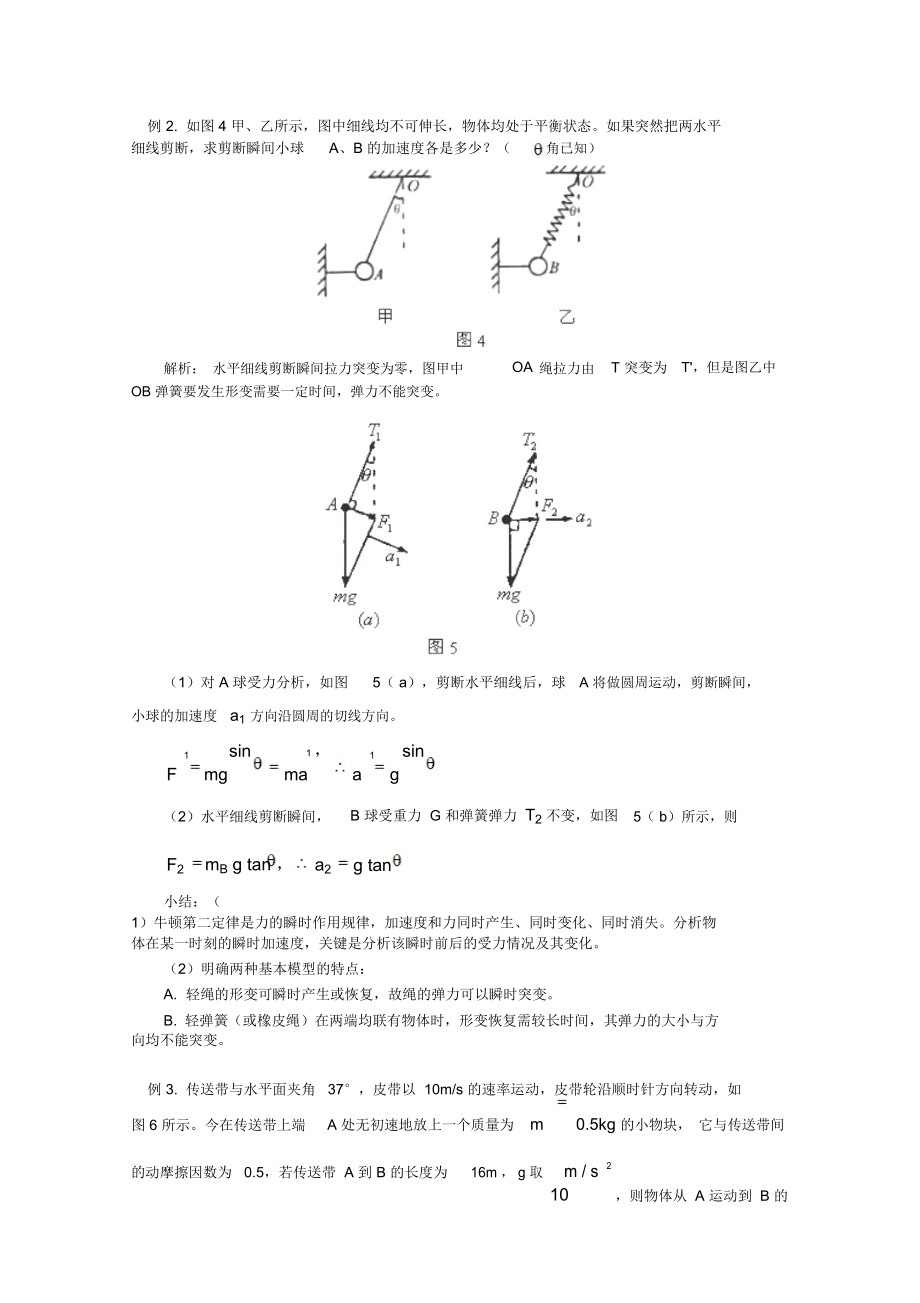
8、 A 的加速度 a2ga' ，所以小球将飘离滑块A，其受力如图3 所示，设线和竖直方向成角，由小球水平竖直方向状态可列方程T sinma'T 'cosmg0解得：T '225mamgmg例 2. 如图 4 甲、乙所示，图中细线均不可伸长，物体均处于平衡状态。如果突然把两水平细线剪断，求剪断瞬间小球A、B 的加速度各是多少？（角已知）解析： 水平细线剪断瞬间拉力突变为零，图甲中OA绳拉力由T 突变为T'，但是图乙中OB 弹簧要发生形变需要一定时间，弹力不能突变。（1）对 A 球受力分析，如图5（ a），剪断水平细线后，球A 将做圆周运动，剪断瞬间，小球的加

9、速度a1 方向沿圆周的切线方向。1mgsin1 ，1gsinFmaa（2）水平细线剪断瞬间，B 球受重力 G 和弹簧弹力 T2 不变，如图5（ b）所示，则F2mB g tan ，a2g tan小结：（ 1）牛顿第二定律是力的瞬时作用规律，加速度和力同时产生、同时变化、同时消失。分析物体在某一时刻的瞬时加速度，关键是分析该瞬时前后的受力情况及其变化。（2）明确两种基本模型的特点：A. 轻绳的形变可瞬时产生或恢复，故绳的弹力可以瞬时突变。B. 轻弹簧（或橡皮绳）在两端均联有物体时，形变恢复需较长时间，其弹力的大小与方向均不能突变。例 3. 传送带与水平面夹角 37°，皮带以 10m/s

10、 的速率运动，皮带轮沿顺时针方向转动，如图 6 所示。今在传送带上端A 处无初速地放上一个质量为 m0.5kg 的小物块， 它与传送带间的动摩擦因数为 0.5，若传送带 A 到 B 的长度为16m ， g 取m / s2，则物体从 A 运动到 B 的10时间为多少？解析： 由于静止。0.5tan0.75 ，物体一定沿传送带对地下移，且不会与传送带相对设从物块刚放上到皮带速度达10m/s ，物体位移为 s1 ，加速度 a1 ，时间 t1 ，因物速小于皮带速率，根据牛顿第二定律，a1mg sinmmg cos10m / s2 ，方向沿斜面向下。t1v1s， s11 a1 t125m皮带长度。a12

11、设从物块速率为m / s2到 B 端所用时间为 t，加速度 a，位移 s ，物块速度大于皮带10222速度，物块受滑动摩擦力沿斜面向上，有：a2mg sinmg cos2m / s2ms2vt21 a2 t222即 16510t212t 22 ， t 21s （ t210s 舍去）2所用总时间 tt1t22s例 4. 如图 7，质量 M8kg 的小车停放在光滑水平面上，在小车右端施加一水平恒力F=8N。当小车向右运动速度达到3m/s 时，在小车的右端轻放一质量m=2kg 的小物块， 物块与小车间的动摩擦因数0.2 ，假定小车足够长，问：（1）经过多长时间物块停止与小车间的相对运动？（2）小物块

12、从放在车上开始经过t03.0s 所通过的位移是多少？（g 取 10m / s2 ）解析：（ 1）依据题意，物块在小车上停止运动时，物块与小车保持相对静止，应具有共同的速度。设物块在小车上相对运动时间为t，物块、小车受力分析如图8：物块放上小车后做初速度为零加速度为a1 的匀加速直线运动，小车做加速度为a2匀加速运动。由牛顿运动定律：物块放上小车后加速度：a1g2m / s2小车加速度： a2Fmg/ M0.5m / s2v1a1tv23 a2 t由 v1v2 得： t2s（2 ）物块在前 2s 内做加速度为 a1 的匀加速运动， 后 1s 同小车一起做加速度为a2的匀加速运动。以系统为研究对象

13、：根据牛顿运动定律，由FM m a3 得：a3F / Mm08. m / s2物块位移 ss1s2s11 / 2 a1 t 24ms2v1 t1 / 2 at2244.mss1 s28.4m例 5. 将金属块 m 用压缩的轻弹簧卡在一个矩形的箱中，如图 9 所示，在箱的上顶板和下底板装有压力传感器，箱可以沿竖直轨道运动。当箱以2a./s 的加速度竖直向上做匀减2 0m速运动时，上顶板的传感器显示的压力为6.0 N，下底板的传感器显示的压力为10.0 N。（取g 10m / s2）（ 1）若上顶板传感器的示数是下底板传感器的示数的一半，试判断箱的运动情况。（ 2）若上顶板传感器的示数为零，箱沿竖

14、直方向运动的情况可能是怎样的？启迪： 题中上下传感器的读数，实际上是告诉我们顶板和弹簧对m 的作用力的大小。对m 受力分析求出合外力，即可求出m 的加速度，并进一步确定物体的运动情况，但必须先由题意求出m 的值。解析： 当 a12.0m / s2 减速上升时， m 受力情况如图10 所示：mgN 1N 2ma1mN 2N 1106 kg0.5kgg a1102（1） N2' N210N，N1'N 2'25NN 1 ' mgN 2 '0故箱体将作匀速运动或保持静止状态。（2）若 N1"0 ，则F合N 2 " mg 10 5 N 5NaF

15、合10m / s2 （向上）m即箱体将向上匀加速或向下匀减速运动，且加速度大小大于、等于10。m / s2例 6. 测定病人的血沉有助于对病情的判断。血液由红血球和血浆组成，将血液放在竖直的玻璃管内，红血球会匀速下沉，其下沉的速度称为血沉，某人血沉为v，若把红血球看成半径为 R 的小球，它在血浆中下沉时所受阻力f6 Rv ，为常数，则红血球半径R_。（设血浆密度为0 ，红血球密度为）解析： 红血球受到重力、阻力、浮力三个力作用处于平衡状态，由于这三个力位于同一竖直线上，故可得mg0 gVf即4 R 3 g0 g 4 R36 Rv33得： R9 v0 g21. 如图 1 所示，在原来静止的木箱内

16、，放有A 物体， A 被一伸长的弹簧拉住且恰好静止，现突然发现A 被弹簧拉动，则木箱的运动情况可能是（）A. 加速下降B. 减速上升C. 匀速向右运动D. 加速向左运动2. 如图 2 所示，固定在水平面上的光滑半球，球心O 的正上方固定一个小定滑轮，细绳一端拴一小球，小球置于半球面上的A 点，另一端绕过定滑轮，如图所示。今缓慢拉绳使小球从 A 点滑到半球顶点，则此过程中，小球对半球的压力大小N 及细绳的拉力T 大小的变化情况是（）A. N 变大，C. N 不变，T 变大T 变小B. N变小， T变大D. N变大， T变小3. 一个物块与竖直墙壁接触，受到水平推力F 的作用。力 F 随时间变化的

17、规律为Fkt（常量 k>0）。设物块从 t0 时刻起由静止开始沿墙壁竖直向下滑动，物块与墙壁间的动摩擦因数为1，得到物块与竖直墙壁间的摩擦力f 随时间t 变化的图象， 如图3 所示， 从图线可以得出（）A. 在 0 t1 时间内，物块在竖直方向做匀速直线运动B. 在 0 t1 时间内，物块在竖直方向做加速度逐渐减小的加速运动C. 物块的重力等于 aD. 物块受到的最大静摩擦力总等于b4. 如图 4 所示，几个倾角不同的光滑斜面具有共同的底边AB，当物体由静止沿不同的倾角从顶端滑到底端，下面哪些说法是正确的？（）A. 倾角为 30°时所需时间最短B. 倾角为 45°所需

18、时间最短C. 倾角为 60°所需时间最短D. 所需时间均相等5. 如图 5 所示，质量为M 的木板，上表面水平，放在水平桌面上，木板上面有一质量为m的物块，物块与木板及木板与桌面间的动摩擦因数均为，若要以水平外力F 将木板抽出，则力 F 的大小至少为（）A.mgB.Mm gC.m2 M gD. 2Mm g6. 一个质量不计的轻弹簧，竖直固定在水平桌面上，一个小球从弹簧的正上方竖直落下，从小球与弹簧接触开始直到弹簧被压缩到最短的过程中，小球的速度和加速度的大小变化情况是（）A. 加速度越来越小，速度也越来越小B. 加速度先变小后变大，速度一直是越来越小C. 加速度先变小，后又增大，速度

19、先变大，后又变小D. 加速度越来越大，速度越来越小7. 质量m1kg 的物体在拉力F 作用下沿倾角为30°的斜面斜向上匀加速运动，加速度的大小为a3m / s2 ，力F 的方向沿斜面向上，大小为10N。运动过程中，若突然撤去拉力F，在撤去拉力F 的瞬间物体的加速度的大小是_；方向是_。8. 如图 6 所示，倾斜的索道与水平方向的夹角为37°，当载物车厢加速向上运动时，物对车厢底板的压力为物重的1.25 倍，这时物与车厢仍然相对静止，则车厢对物的摩擦力的大小是物重的 _倍。9. 如图 7 所示，传送带 AB 段是水平的，长 20 m，传送带上各点相对地面的速度大小是2 m/s

20、 ，某物块与传送带间的动摩擦因数为0.1。现将该物块轻轻地放在传送带上的A 点后，经过多长时间到达B 点？（ g 取102）m / s10. 鸵鸟是当今世界上最大的鸟。有人说它不会飞是因为翅膀退化了，如果鸵鸟长了一副与身体大小成比例的翅膀，它是否就能飞起来呢？这是一个使人极感兴趣的问题，试阅读下列材料并填写其中的空白处。鸟飞翔的必要条件是空气的上举力F 至少与体重Gmg 平衡，鸟扇动翅膀获得的上举力可表示为F cSv2 ，式中 S 为鸟翅膀的面积， v 为鸟飞行的速度， c 是恒量，鸟类能飞起的条件是 FG ，即 v _，取等号时的速率为临界速率。我们作一个简单的几何相似性假设。设鸟的几何线度

21、为l ，质量 m 体积l 3 ， S l 2 ，于是起飞的临界速率 vl 。燕子的滑翔速率最小大约为20 km/h ，而鸵鸟的体长大约是燕子的 25倍，从而跑动起飞的临界速率为_km/h ，而实际上鸵鸟的奔跑速度大约只有40km/h ，可见，鸵鸟是飞不起来的，我们在生活中还可以看到，像麻雀这样的小鸟，只需从枝头跳到空中，用翅膀拍打一两下，就可以飞起来。而像天鹅这样大的飞禽，则首先要沿着地面或水面奔跑一段才能起飞，这是因为小鸟的_，而天鹅的 _。11. 如图 8 所示， A 、 B 两个物体靠在一起放在光滑水平面上，它们的质量分别为M A 3kg， M B6kg 。今用水平力 FA 推 A，用水

22、平力 FB 拉 B， FA 和 FB 随时间变化的关系是 FA 9 2tN 、FB3 2t N 。求从 t=0 到 A、 B 脱离，它们的位移是多少？12.质量为如图 9 所示，在倾角为的长斜面上有一带风帆的滑块，从静止开始沿斜面下滑，滑块m，它与斜面间的动摩擦因数为，帆受到的空气阻力与滑块下滑速度的大小成正比，即 fkv 。（ 1）写出滑块下滑加速度的表达式。（ 2）写出滑块下滑的最大速度的表达式。（3）若m2.0kg，30 ，g10m / s2 ，从静止下滑的速度图象如图所示的曲线，图中直线是t 0 时的速度图线的切线，由此求出和 k 的值。13. 如图10 所示，一个弹簧台秤的秤盘和弹簧

23、质量均不计，盘内放一个质量m12kg 的静止物体P，弹簧的劲度系数k800N / m。现施加给P 一个竖直向上的拉力F，使P 从静止开始向上做匀加速运动。已知在头0.2s 内F 是变力， 在0.2s 以后， F 是恒力，取g10m / s2 ，求拉力F 的最大值和最小值。【试题答案】1. ABD解析： 木箱未运动前，A 物体处于受力平衡状态，受力情况：重力mg、箱底的支持力N、弹簧拉力F 和最大的静摩擦力f m （向左），由平衡条件知：mgN， Ff m物体A 被弹簧向右拉动（已知），可能有两种原因，一种是弹簧拉力Ff m ' （新情况下的最大静摩擦力） ，可见f mf m '

24、 ，即最大静摩擦力减小了，由 f mN知正压力N 减小了，即发生了失重现象，故物体运动的加速度必然竖直向下，由于物体原来静止，所以木箱运动的情况可能是加速下降，也可能是减速上升，A对 B也对。另一种原因是木箱向左加速运动，最大静摩擦力不足使A 物体产生同木箱等大的加速度，即mgkxmamg 的情形，D 正确。匀速向右运动的情形中由静止改做匀速运动的情形，A 的受力情况与原来静止时C 错。A 的受力情况相同，且不会出现直接2. C小球受力如图 11（甲），T、 N、 G 构成一封闭三角形。由图 11（乙）可见，AOB ANTT/ABN /OAG/OBTGAB/OBNGOA/OBAB 变短， OB

25、 不变， OA 不变，故T 变小， N 不变。3. BC在 0 t 1 时间内，物块受到的摩擦力小于物块受到的重力，物块向下做加速运动，A 错。滑动摩擦力随正压力的增大而逐渐增大，合外力逐渐减小，加速度逐渐减小，B 对。当摩擦力不再随正压力的变化而变化时，一定是静摩擦力了。静摩擦力的大小恰好与重力平衡，所以物块受的重力等于a， C 对。最大静摩擦力随正压力的增大而增大，不会总等于b， D 错。4. B解析： 设沿一一般斜面下滑，倾角为，长为l，物体沿斜面做初速为零加速度为ag sin的匀加速直线运动，滑到底端的时间为t ，则有：l1 g sin t 212lAB / cos2<1>

26、<2>联立解得： t2 AB4 ABg sin cosg sin 2所以当 290 ，45 时， t 最小，故选 B。5. D解析： 将木板抽出的过程中，物块与木板间的摩擦力为滑动摩擦力，m 的加速度大小为amg ，要抽出木板，必须使木板的加速度大于物块的加速度，即a M amg ，对木板受力分析如图12，根据牛顿第二定律，得：FMm gmg Ma MFM m g mg Ma MM m g mg Mg 2 M m g选项 D正确ammg(M+m )gF图 126. C当弹簧的弹力等于重力时，小球的速度最大，a0 。7. 7m / s2 ，沿斜面向下有拉力时， Fmg sin 30f ma代入 a 3m /s2 ，求得 f2 N撤 F 瞬间， fmg sin 30ma8. 0.33提示： N mg may ， f 静maxa y，tg37ax9. 11s提示： 物块放到 A 点后先在摩擦力作用下做匀加速直线运动，速度达到2m/s 后，与传送带一起以 2m/s 的速度直至运动到B