超精密磁悬浮工作台及其解耦控制-

1、第40卷第9期2004年9月机械工程学报CHINESE JOURNAL OF MECHANICAL ENGINEERINGSep. 2004超精密磁悬浮工作台及其解耦控制*李黎川(西安交通大学电气工程学院西安 710049丁玉成卢秉恒(西安交通大学机械工程学院西安 710049摘要:给出了一个磁悬浮工作台的结构设计、建模、控制器设计、实时控制试验和试验结果。与国际上已有的类似研究相比,给出的方案使磁悬浮部分独立于直线电动机,以避免两者间的耦合问题。此外,在电磁铁的结构和传感器的布置上,均给出了全新的设计,其特点是即便不使用永久磁铁,电磁铁的静态功耗也比较小,以及在驱动和位置检测上安排了冗余。后

2、者的有利之处是可获得结构上的对称性和解耦后各控制通道在噪声性能上的一致性,且能够更大程度地降低位移信号中的噪声,代价是需要增加一路位移传感器和功率放大器,以及需要略多的实时计算以实现解耦和消除冗余。关键词:精密运动控制精密工作台磁悬浮解耦控制磁悬浮轴承0 前言为了实现精密运动控制,典型的方法是采用精密导轨,旋转电动机,精密丝杠构成运动控制的前向通道,然后由光栅构成位置反馈通道并施行闭环控制,与之相关的一整套技术已十分成熟,所能获得的典型精度已达到0.1 m的数量级。但若要采用这一结构获得更高的精度(比如10 nm,无论是技术上还是经济上都遇到了明显的困难,这主要是由于系统中各个运动副之间存在库

3、仑摩擦1,2。此外,在要求实现多自由度运动控制的场合,若采用导轨和轴承作为支承部件,系统的机械结构会随着自由度的增加而变得十分复杂,且使得刚度不容易提高,运动控制的精度更加难以保证。目前,国内外在诸如超精密加工、微型机械的制造和装配、集成电路工艺和扫描隧道显微镜等领域,对超精密运动控制的性能要求越来越高,其中对运动控制精度的要求已达到纳米数量级。鉴于传统的运动控制结构和方式已经不能满足上述场合的要求,采用新技术实现超精密运动控制的研究已成为目前国内外的一个研究热点,其中的一个主要技术手段是采用磁悬浮代替传统的机械导轨3,4。采用磁悬浮技术(以及直线电动机直接驱动实现超精密运动控制,可以完全消除

4、库仑摩擦,因而国家自然科学基金资助项目(59975073。20031026收到初稿,20040425收到修改稿可以获得很高的精度。此外,采用磁悬浮的一个很突出的好处是系统的机械结构反而变得简单了,有精度要求的部件也大大减少。目前采用磁悬浮技术实现精密定位的最好结果已达到3 nm 5。参考文献3,4分别给出了两种磁悬浮工作台的设计与实现,前者采用固定在工作台底部的Halbach永久磁铁阵列来产生罗仑兹力以悬浮和驱动工作台,其特点是结构简单巧妙,直线电动机与磁悬浮部分共用永久磁铁和线圈,但由于采用Halbach阵列,工作台移动时磁悬浮部分也需要换向,因而当工作台高速移动时会有波动,影响跟随精度,此

5、外这种结构的静态功耗较大;后者采用了三个与磁悬浮轴承类似的结构(其中包含永久磁铁,将工作台定位于水平面内(基于三点决定一个平面的原理,其直线电动机使用磁悬浮部件中已建立的磁场,结构也比较巧妙,其主要特点是磁悬浮的功耗小,但直线电动机与磁悬浮部分有电气上的耦合是其不理想之处。1 磁悬浮结构设计工作台的磁悬浮大致有两种方案,一种是采用罗仑兹力3,另一种是采用电磁力4。前者的特点是可以通过改变电流的方向而使罗仑兹力反向,且线性好,但功耗大。后者只能产生吸引力,具有明显的非线性,但功耗小。考虑到功耗是一个重要因数(因为温升对精密系统是很不利的,采用了电磁力2004年9月李黎川等:超精密磁悬浮工作台及其

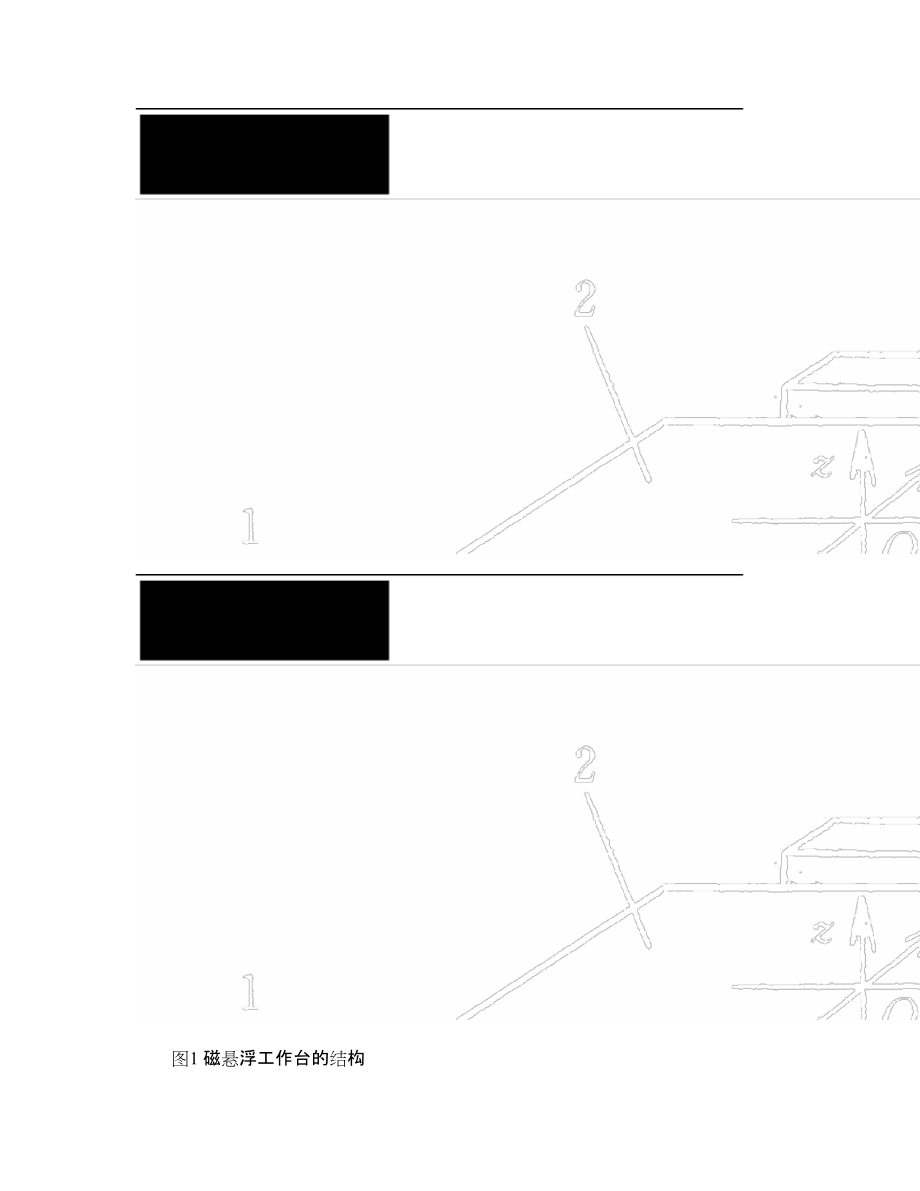
6、解耦控制85的方案。由于电磁力只能是吸引的,因此在工作台的上方必须有电磁铁以平衡重力,这在一定的程度上会影响工作台台面上工件的安放,不过这一问题可以通过将电磁铁在重力方向上的尺寸设计得尽量小而得到缓解。顺便指出,若采用永久磁铁,则可将其固定在工作台的底部,并由安排在工作台下方的载流绕组产生罗仑兹力,以平衡工作台的重力。通过多种方案的比较,最后选择了如图1所示的结构,图2为对应物理系统的照片。两个电磁铁的结构和尺寸完全相同,如图3所示。为了尽量避免工作台上方电磁铁对工件安放的影响,只采用了两个电磁铁,但由于每个电磁铁有三个磁极和两个独立的绕组,因而仍可以对工作台的其中3自由度进行控制(z轴方向上

7、的平动和绕x和y轴的转动。工作台的另外3自由度将由图中所示的平面电动机控制,不涉及这一部分,只讨论磁悬浮部分。 图1 磁悬浮工作台的结构1、3. 电磁铁 2. 工件安放表面 4. 狭缝用于平面电动机 5. 工作台 图2 磁悬浮工作台1、3. 电磁铁 2. 工件安放表面 4. 传感器 图3 电磁铁的结构由于采用了固定电磁铁的方案,在工作台移动时,其质心位置相对于电磁铁在不断变化,造成系统动特性的变化。但这一问题并不突出(见试验结果,因工作台在x和y轴上的设计行程只有±10 mm,大致是工作台尺寸的十分之一。2 被控对象模型及解耦建立磁悬浮工作台的模型的基本原理及方法与磁悬浮轴承的类似,

8、都是基于磁路定理,忽略漏磁、边沿效应以及铁磁材料的磁阻,首先获得对象的非线性模型,然后在平衡位置处对非线性模型进行线性近似,得到一个线性模型,以此作为分析被控对象和设计控制器的基础6。为了简化推导过程,首先定义平衡位置下的所有物理量,然后直接写出线性模型,同时给出文字上的解释以说明线性模型的正确性。在系统中,所谓平衡位置,是由这样一些特征规定的(参见图4:工作台在xy平面内处于中央位置,所有磁极极面与工作台的距离(气隙均为g,四个线圈的电流均为I0,(同时端电压均为U0,磁通均为0,因此电磁铁中央磁极无磁通,磁极1、磁极2、磁极3和磁极4对工作台的电磁力之和与工作台的重量平衡。表1给出了对象的

9、一些物理参数,以及平衡位置下的一些物理量及其数值。表2给出了相对于平衡位置下的物理量的变化量,由于平衡位置下关于转动的量均为零,因此表2中与转动有关的量就是绝对量,只有与z方向有关的量以及磁通、电流和电压为相对变化量。 图4 电磁铁的布置机 械 工 程 学 报 第40卷第9期86表1系统参数的符号及数值 表2有关变量的符号及定义 由于两个电磁铁相同,先给出一个电磁铁的模型,然后在此基础上给出整个磁悬浮系统的模型,这样可以使叙述有层次和更简洁。对电磁铁1,可以列出111u Ri N =+& (1 222u Ri N =+& (2 (2(5.0(21211110+=z z g z

10、g ANi (3 (2(5.0(21212220=z z g z g ANi (4注意式(3、(4即磁路定理以及0.5(2g - z 1 - z 2为中央磁极处的气隙。将式(3、(4中的i 1和i 2分别代入式(1、(2并略去高次项,得到磁通的变化率的线性近似为 1211011424u NK Rg K Rg z K R +=& (5 2212021244u N K Rg K Rg z K R +=& (6 式中K = 0AN 2/4为一个惯用的常数。由于在平衡位置下中央磁极处磁通为零,因此在线性近似后这里的电磁力也为零,这样,只需要考虑磁极1和磁极2处的力。根据在平衡位置下磁通

11、均为0,可直接写出磁极1和磁极2处的电磁力分别为1001(F A = (72002(F A = (8 由于磁通与电磁力为代数关系,可将式(7、(8中的1和2代入式(5、(6,消去磁通,得到关于力的微分方程(到这里将电磁铁2的方程同时写出为20011121224RI I Rg Rg F z F F u K K g g=+& (920022122242RI I Rg Rg F z F F u K K g g =+& (1020033343224RI I Rg Rg F z F F u K K g g =+& (1120044344242RI I Rg Rg F z F F

12、u K K g g=+& (12至此已得到了从四个电压到四个力的动态关系,下面将根据工作台的质量及转动惯量列写出运动方程,最后得到从电压到位移的传递关系。这里需要提及的是,所采用的是电压控制(被控对象的输入是电压,与通常所采用的电流控制(被控对象的输入是电流相比较,电压控制虽然使被控对象的阶数略高一些,但没有电流控制所隐含的纯微分环节(该微分环节尽管实际上只是一个有限带宽微分,但带宽通常必须高达数千赫兹,这就使得系统对噪声比较敏感。根据图1和图4所示的结构,可以写出磁悬浮所涉及的3自由度的运动方程为1234Mz F F F F =+&& (133412(J F F F

13、F b =+&& (14 1324(J F F F F a =+&& (15 对式(9(12以及式(13(15中的每个方程的两端取拉氏变换,然后消去f 1,f 2,f 3,f 4,并采用下面的坐标变换(注意该变换只在和很小时成立4(4321z z z z z += (16b z z z z 4(2143+= (17a z z z z 4(4231+= (18以及下面的输入变换u u u u z +=1 (19 u u u u z =2 (20 u u u u z +=3 (21u u u u z +=4 (22 最后经代入和化简可得到三个解耦的传递函数如下 M

14、g RI s K Rg s gM I s u s z z 22023044(4(+= (23 J g b RI s K Rg s gJ b I s u s 222023044(4(+= (24 J g a RI s K Rg s gJ a I s u s 2220230443(4(+= (25 注意式(23(25都是(开环不稳定的。由这三个传递函数,便可以独立地设计三个单输入单输出的控制2004年9月李黎川等:超精密磁悬浮工作台及其解耦控制87器,对相应的 3 自由度进行镇定和控制。3 控制器设计对于式(23(25所示的三个被控对象,由于其结构相同,所采用的控制器结构也相同。下面只给出z轴的设

15、计,其余两个方向的情况仅仅是参数值不同。控制回路的形式如图5所示,其中包含一个积分器、一个镇定控制器和一个抗饱和环节(关于所采用的抗饱技术的细节见参考文献1,r z为参考输入,正常情况下为零。三个控制轴上的参考输入的组合,便可以控制工作台的部分姿态(其余部分由平面电动机控制。 图5 闭环控制结构由于被控对象为3阶,积分和镇定控制器共3阶,因此闭环系统为6阶。这样,闭环传递函数的极点恰好可以由图5中的6个参数(C,B2,B1,B0,A1,A0任意配置。将表1中的参数值代入式(23(25可计算出三个传递函数均有一个右极点,分别为136.5、185.8和110.4(可见它们的不稳定模态速度相当,因而

16、对控制是很有利的。通常情况是,将全部闭环极点配置在负实轴上,且幅值大致为4倍开环右极点的幅值时,可获得较好的综合性能(动态响应、传感器噪声抑制和鲁棒性等7,8。这样,三个控制环的闭环极点全部配置在2×120处(120 Hz的闭环带宽,由此可计算出每个控制通道的6个控制器参数。值得一提的是,将镇定控制器安排在反馈通道上,使得参考输入不通过该控制器,其目的是为了减少阶跃输入时的超调(因镇定控制器的高频增益通常都很大,另一方面,由于误差信号通过积分器,因此稳态误差为零。4 试验及结果整个控制系统的结构如图6所示。在工作台的底部,且恰好在四个磁极的下方,安装了四个相同的电容位移传感器(量程&

17、#177;50 m,方均根噪声4 nm,带宽5 000 Hz,由此可以测得式(16(18右端的四个位移量并经变换得到三个控制器输入(传感器的安装使得工作台在平衡位置时传感器输出正好为零。控制器输出经式(19(22变换后给出四个被控对象输入(需加上平衡位置下的电压U0,经功率放大后独立地驱动四个线圈。功率放大器的峰值输出电压和电流分别为±10 V和+4 A,带宽约20 kHz。A/D转换的分辨率为16位(8 s转换时间,分时复用,D/A为14位(0.01%调整时间约5 s。采样周期取为100s,积分器和镇定控制器都按这一采样周期离散化(采用MATLAB中的c2d函数及zoh选项,然后用

18、C语言编写相应的控制程序,实时运行于DOS平台。 图6 试验系统的结构上述试验系统在加电并启动控制程序后,工作台被悬浮在平衡位置。由于平面电动机尚未安装运行,且由于系统不能绝对水平地安装,工作台悬浮后向某一方向“流动”以至碰到限位挡块。为解决这一问题,在工作台的工件安放表面固定了两片永久磁铁,同时在这两片永久磁铁的正上方约3 mm处,以相吸引的极性固定了另外两片永久磁铁。这样,工作台悬浮后便可停留在中间某个位置。注意这些永久磁铁只非常略微地改变了工作台的动态特性,完全可以忽略。为了观察闭环系统的性能以及三个控制轴之间的解耦情况,分别对三个控制环施加5 Hz的方波参考输入。z轴的参考输入在0和1

19、0 m之间变化,和轴的参考输入分别在0和10 m/b= 0.125 mrad之间以及0和10 m/a= 0.25 mrad之间变化。考虑到以毫弧度为单位的旋转量不如以微米为单位的位移量更为人们所熟悉,且为了便于三个控制轴之间的比较,在观察系统的输出响应时,不直接给出和这两个输出变量,而是给出按下式定义的两个与和成比例的变量4(2143zzzzbz+=(264(2143zzzzaz+=(27 注意这两个变量为旋转时磁极(或传感器处的对应位移量。由于当工作台处于平衡位置时原理上就不存在耦合,因此在施加参考输入时,通过调整永久磁铁的位置,将工作台分别在x和y的正方向上移动了5 mm。在工作台被悬浮且

20、xy平面中的暂态过程(由永机械工程学报第40卷第9期88久磁铁引起消失后,施加参考输入,同时采集数据,得到了如图7所示的结果。为便于观察,图中未施加参考输入的控制环的输出,在绘图时分别被下移了2 m和4 m。由图7可以看出,除轴的阻尼特性不够好之外,三个控制环有预期的闭环动态响应特性以及良好的解耦效果。关于轴阻尼不足的问题,尚未进一步探究。最后值得一提的是,虽然所用的位移传感器其方均根噪声只有4 nm,因而开环时变量z中的方均根噪声只有2 nm,但闭环系统处于稳态时z中的方均根噪声却高达26.8 nm(这样大的差异在传感器的方均根噪声为微米量级时一般是不会出现的,比如采用电涡流位移传感器时。这

21、一现象在一定的程度上是由于电气和机械干扰的原因,是否还与其他因素有关,还需要进一步研究。 图7 施加参考输入时三个控制轴的位移输出5 结论(1 所提出的设计方案基于四个位置检测和四个电磁力驱动,与基于三点决定一个平面的原理相比较,虽然多用了一路传感器和功率放大器,但所涉及的3自由度上的位移信号在坐标变换后均来自四个传感器,从而能够更有效地降低位移信号中的噪声,并获得结构上的对称性。(2 工作台由磁悬浮所控制的3自由度之间的耦合,通过输入与输出空间中的坐标变换就可以消除,而不需要状态反馈。(3 若采用传统的机械结构支撑工作台,至少需要三层机械结构(一层x导轨、一层y导轨和一层回转导轨,如果还要求

22、z方向上的移动以及绕x和y轴的转动,机械结构将更为复杂,此外这当中对许多部件有很高的精度要求。采用磁悬浮支撑工作台,系统的机械结构则大大简化,有精度要求的部件只有工作台底部的平面度和表面粗糙度(位移传感器的目标平面。(4 运动控制的分辨率深入到纳米量级时,系统的位置分辨能力对许多因素将变得很敏感,这时每一个有可能渗入机械和电气噪声的环节都需要细致的设计和实施。参考文献1 Mao J, Tachikawa H, Shimokohbe A. Precision positioningof a DC-motor-driven aerostatic slide system. Precision En

23、gineering, 2003, 27(1:32412 Zhang B, Zhu Z. Developing a linear piezomotor withnanometer resolution and high stiffness. IEEE/ASME Trans. Mechatronics, 1997, 2(1:22293 Kim W, Trumper D L. Six-degree-of-freedom planar posi-tioner with linear magnetic bearing/motors. In:allaire P E ed.Proc. 6th Int. Symp. on Mag