生物医学信号处理习题集第一章生物医学信号概论

1、生物医学信号处理习题集第一章 生物医学信号概论1. 生物医学信号处理的对象是什么信号？解答：包括生理过程自发产生的信号，如心电、脑电、肌电、眼电、胃电等电生理信号和血压、体温、脉搏、呼吸等非电生理信号；还有外界施加于人体的被动信号，如超声波、同位素、X 射线等。2. 生物信号的主要特点是什么？解答：随机性强，噪声背景强。第二章 数字信号处理基础You can use Matlab where you think it s appropriate.1.FIR 滤波器和IIR 滤波器的主要区别是什么？解答：FIR 滤波器的单位脉冲响应是有限长的序列，该滤波器没有极点，具有稳定性。IIR 滤波器的单

2、位脉冲响应是无限长的序列，该滤波器有极点，有可能不稳定。-12-12.两个滤波器级联，第一个的传递函数为H1(z) 1 2z z ，第二个为H2(z) 1 z ，当输入为单位脉冲时，求输出序列，画出级联滤波器的频率响应。 解答：-121H(z) (1 2z z )(1 z )=1 z-1 z2 z3h(n)=1,1,-1,-1 ， n=0， 1， 2， 3。即输入单位脉冲时的输出序列值。 freqz(h,1)口co厂T d H a I A. &,11D.2 a J ： 4 OE QB 07 口 E二 9hhrirRliT-d -rr|i.»rry (>riO 司 HEG

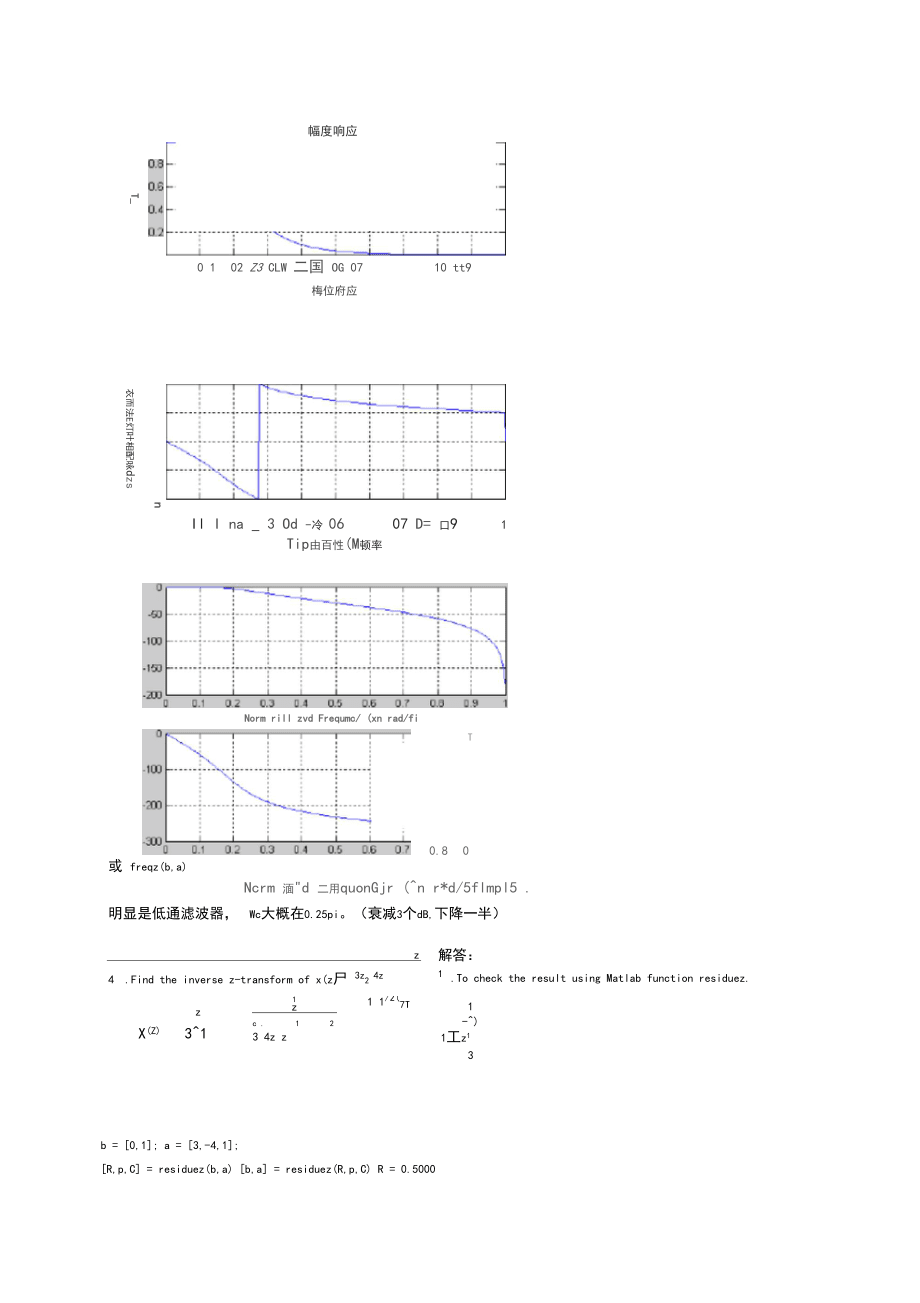
3、prl*?至G-2C.10.2 口 304 U5 OD 07 O.S Q.91hkirmalized Frauuericy (xnrad/sPinole)m n m1 1 一一98816 曹0)fl'mwEL3 .A 3rd-order lowpass filter is described by the difference equation:y(n) 0.0181x(n) 0.0543x(n 1) Q0543x(n 2) 0.0181x(n 3)1.76y(n 1) 1.1829y(n 2) 0.2781y(n 3)Plot the magnitude and the phase

4、response of this filter and verify that it is a lowpass filter. 解答：b = 0.0181,0.0543, 0.0543, 0.0181;a = 1.0000, -1.7600, 1.1829, -0.2781;m = 0:length(b)-1; l = 0:length(a)-1;K = 500; k = 1:1:K;w = pi*k/K; % 0, pi分成 501 个点.num = b * exp(-j*m'*w); %分子计算den = a * exp(-j*l'*w); %分母计算H = num ./

5、den;magH = abs(H); angH = angle(H);subplot(1,1,1);subplot(2,1,1); plot(w/pi,magH); grid; axis(0,1,0,1)xlabel(''); ylabel('|H|');title('幅度响应');subplot(2,1,2); plot(w/pi,angH/pi); grid on; axis(0,1,-1,1)xlabel('以pi为单位的频率');ylabel('以pi弧度为单位的相位');title('相位响应&#

6、39;);T_幅度响应0 102 Z3 CLW 二国 OG 0710 tt9梅位府应n 5 n 5 57 a Q 4衣而法E灯叶相配咏dzsNorm rill zvd Frequmc/ (xn rad/fi arnMT0.80 9Il I na _ 3 Od -冷 0607 D= 口91Tip由百性(M顿率或 freqz(b,a)Ncrm 湎"d 二用quonGjr (n r*d/5flmpl5 .明显是低通滤波器，Wc大概在0.25pi。（衰减3个dB,下降一半）z4 .Find the inverse z-transform of x(z尸 3z2 4z解答：1 .To chec

7、k the result using Matlab function residuez.zX(Z)311zc .123 4z z1 1/2(7T1-)1工z13b = 0,1; a = 3,-4,1;R,p,C = residuez(b,a) b,a = residuez(R,p,C) R = 0.5000-0.5000p = 1.00000.3333C = 口b = -0.00000.3333a = 1.0000-1.33330.3333笔算和程序结果一致。5.Choose an appropriate window to design a digital FIR lowpass filte

8、r with the following specifications:p 0.2 ,Ap 0.25dB s 0.3 ,As 50dB ,Determine the impulse response and provide a plot of the frequency response of the designed filter. (help fir1 function ) 解答：wp = 0.2*pi; ws = 0.3*pi;tr_width = ws -wp ;M = ceil(6.6*pi/tr_width) ; %查表求得窗长度，hamming window 即可n=0:1:M-

9、1;wc = (ws+wp)/2b= fir1(M,wc/pi);h=b(1:end-1);hh,w = freqz(h,1,'whole');% 默认就是 hamming windowhhh=hh(1:255);ww=w(1:255);%画图subplot(2,2,3); stem(n,h);title('实际脉冲响应')axis(0 M-1 -0.1 0.3); xlabel('n'); ylabel('h(n)')subplot(2,2,4); plot(ww/pi,20*log10(abs(hhh);title('

10、幅度响应(单位:dB) ');gridaxis(0 1-100 10); xlabel('频率(单位:pi) '); ylabel('分贝')set(gca,'XTickMode','manual','XTick',0,0.2,0.3,1)set(gca,'YTickMode','manual','YTick',-50,0)实际脉冲响应0.3 I幅度响应（单位：犯）0.2'020 4Q 印频率（单位：pi）第三章随机信号基础1.什么是平稳各态遍历的随机

11、过程？解答：如果随机信号的统计特性与开始进行统计分析的时刻无关，则为平稳随机过程，否则为非平稳随机 过程。对于平稳过程，如果所有样本在固定时刻的统计特征和单一样本在全时间上的统计特征一致, 则为各态遍历的随机过程。平稳且各态遍历是本课程分析医学信号的一个前提假设2.判断随机相位正弦波在均值意义下是否各态遍历。x Asin( 0t) , a0是固定值，是随机变量，分布为均匀分布:解答：该随机过程的时间平均为:该随机过程的总体平均为:P(mxE(x)Tim 5 :Asin ( 0txp(x)dx-A,其它为零。)dt2Asin ( 0100)P( )d2xxnee-2xndx00-2x ne dx

12、n00.5 de2"0.5(e2xn)0一0 =0.5因此该过程在均值意义下是各态遍历的O3 .讨论相互独立、互不相关、相互正交的区别和联系。解答：随机变量统计独立的条件为：p(x,y) p1、x2都是具有上述分布的随机序列，求 E(y)。解答：E(xn)xnP(xn)dxn0 x n 2e-2x n dx n0 - x n de2 np(y)互不相关的条件为：cov(x, y) 0正交的条件为：E(xy) 0对于一般的随机变量：统计独立则互不相关；当其中有任意一个变量的均值为零，则互不相关和正 交可以互相推导。对于高斯随机变量，统计独立和互不相关可以相互推导；当其中有任意一个变量的

13、均值为零，则三 者都能互相推导。2xn4 .输入序列Xn的一阶概率密度函数是P(xn)eu(xn)。证明：E(xn)0.5y 2x1因为16°,所以含有直流分量;x2E (y) =E(2xi+4x2)=E(2xi)+E(4x2)=35 .已知平稳随机过程 x的自相关函数如下，求其功率谱密度及均方，并根据所得结果说明该随机过 程是否含有直流分量或周期性分量。r j r Rx( ) 4e cos cos3(ii) Rx( ) 25e4| 'cos o 16解答： i11Px( ) Rx( )ej d (3 )(3 ) 8-2-21()1()一 2_E(x ) Rx(0) 4 1

14、5Px(0) 因为o,所以含有直流分量;因为周期信号的自相关函数也是周期性的，而R中包含有一个周期性的成分，因此该随机过程含有周期性分量。Px( ) Rx( )e j d (ii)132( ) 50-216 ( o)1w-"(072E(x ) Rx(0)25 16412Px( ) Rx( T) Rx( T)ej d2Px( )1 e j T ej T2Px ( )(1 cos T),得证。7.一个随机信号xi(t)的自相关函数是R1( ) Aie",另一个随机信号x2的自相关函数 为R2( ) A2e,在下列条件下，分别求信号相加后 X(t)“X2(t)的自相关函数Rx()

15、。(i) X,X2相互独立；(ii) X1，x2来自同一信号源，只是幅度差一个常数因子K (K不为1)： x2=KX1。解答：(i) X1,X2相互独立Rx( ) E(X(t)X(t )E(Xi(t) X2(t)(Xi(t ) X2(t )EXi(t)Xi(t ) X2(t)X"t) Xi(t)X2(t ) X2(t)X2(t)Ri( ) EXi(t)EX2(t ) EXi(t )EX2(t) R2()2limRi()limEXi(t)Xi(t) E(Xi(t) E(Xi(t )E2Xi(t)_2- 2E xi(t) 0,同理 E 风0Rx( ) Ri( ) R2( ) (A1 A2

16、)e"(ii) X2=KX1由前面计算可得 Rx( )Ri( ) EXi(t)x2(t ) EXi(t)x2(t) R2()Ri( ) EXi(t)Kx) EXi(t )KXi(t) R2()Ri( ) 2KRi( ) R2()(A1 2KA1 A2)e 11v2yn l(Xn Xnl)8.Xn是零均值，方差为x的白噪过程，把它先送入一个平均器，得y 2(，然后再将力送给一个差分器zn ynYn 1 ,求Zn的均值、方差、自相关函数和功率谱密度。解答：zn Yn Yn 112 (xn、1,、1,xn 1) (x n-1 x n 2) 大(Xn22xn 2)1E(zn)E(2(xn x

17、n2) 。x22)1 212X/2=Rzn(0)2 E 2、E2E-(xn xn 2) E (xn 2xnxn 2z E(zn) E (zn)441 ，R (1)E (xn xn 2)(x n 1 xn 1 )zn ( ) = E(znzn 1)4=01 , RM2)=E(znzn 2) E4(xn xn 2)(xn 2 xn)=_ x/4 当|m|>=3,自相关都为0。1211Rzn(m)= 2x(m)122)之(m2)121-jw21jw212口pzn(w)2x12e2e2x1cos2w9.随机序列xn各次采样互相独立，且均匀分布于11之间，设ynxnxn 1yn、Zn、Wn的自相关

18、函数和znxn 2xn 1xn2,Wn0.5Wn 1*n,求*n的均值和方差;功率谱。解答：1均值：E(xn)xnP(xn)dxn = 1xn0.5dxn 0均方值：E(Xn) XP(Xn )dXn1 21Xn0.5dXn方差：Var(xn尸_ 2E(Xn)21E (Xn)-3Ryn(0)_2 一E(yn)E(Xn22 -Xn 1) =3E (yn yn 1)E(Xn Xn1)(XnXn)Ryn(2)E(ynyn 2)E(Xn X1)(XXn 1 )当|m|>=2时，y的自相关函数都为零1.C ，、Ryn(m) = 32 (m)(m 1)(m1)Pyn(w)21-jw一 1 e321 j

19、w 2e - 1 cosw23。Rzn(0)2、E(z n ) E( Xn 2 Xn 1、，2X n 2) = 2RZnE(ZnZn 1) E(Xn 2Xn 1 Xn2)(Xn 1 2X nX n 1)RQE(ZnZn 2)E(Xn 2Xn 1 Xn 2)(Xn 2 2XnXn )当|m|>=3时，z的自相关函数都为零1 _Rzn(m)二6 (m) 4 (m 1) 4 (m 1) (m 2) =3(m2)1-jw / jw 2jw j2w _Pzn(w)-6 4e 4e e e 2 8cosw32 cos2w3Rwn(0)E(w2) E(Xn 0.5wn1)2= E(Xn)E(XnWn

20、1)12E(W n 41),、，工.,由于中间一项为零，所以有424Rwn(0) = 3E(Xn)=9,Rwn(1)E(WnWn1) E(X0.5Wn)Wn0.5Rwn(0)Rwn(2)E(WnWn 2) EW(X2 0.5Wn 1)-0.5Rwn(1)2 _0.5) Rwn (0)所以Rw(m)_( 0.5严Rwn(0)4 m9(。5)Pwn()4 mDTFTRwn(m) DTFT® 0.5)网-(j9 1 0.5e j0.5ej1 0.5ej5 cos4第四章数字相关和数字卷积1.设 x=1 2 3 4 ; h=4 3 2 1;求 conv(x,h)、filter(h,1,x)、

21、filter(x,1,h)的结果，并写出后两个函数对应 的传递函数。解答：conv(x,h) =411203020114由于卷积的前后互换性， filter(h,1,x) = filter(x,1,h) = 4112030H1 (z) = 4 3z 1 2z 2 z 3, H2 (z) = 1 2z 1 3z 2 4z 32.输入到线性系统的平稳随机过程x是零均值、方差为1,输出信号的功率谱为j .1Sy(e ) 2，a1 2 a cos a解答：Sx(ej ) 1,0.5,求此系统的传递函数H (Z)。要求该系统稳定。Sy(ej ) Sx(ej )H(ej )因为系统要求稳定j1H(ej)

22、rr,Hj 21H(ej )2 ,a 0.51 2 a cos a11 0.5z 13 .列举相关技术在生物医学信号处理中的部分应用。解答：从噪声中检测信号，例如检测超声脉冲回波。估计两个相似信号的时间延迟，例如测定微血管中的红血球流速，提取脑电诱发响应。 用于生物系统的辨识等。4 .估计相关函数时如果采用 解答：Rx(m)1 N-| m|-1 xnx n mN n 0，估计是否为无偏估计？是否为一致估计?偏差:1 N lm 1ER?x(m)EMxnmN n 0N,ERx(m) Rx(m)m越大，偏差越大，m N时,Rx(m)ERx(m) 0,偏差了 Rx(N)所以不是无偏估计，但 是渐进无偏

23、。估计的方差当N无穷时，趋于零。 因此该估计法是一致估计。5.已知心电图的频率上限约为50Hz,采集数据时候的采样频率至少为多少？如果采样频率为300Hz,要求的频率分辨率为 1Hz,试确定做谱估计时每段数据的点数。解答：由于采样频率至少要为信号最高频率的两倍，所以这时采样频率至少要为100Hz。帚次,fsNN ,可以取工 300，八 t | 一,f ,做谱估计时每段数据的点数要大于512点数据，或者补零到 512点长。300,考虑DFT的计算，最好取 2的第五章维纳滤波x(n) s(n) n(n)y(n) S(n)h(n) 以下三题的系统模型图都参看该图。1.设上图滤波器的方程是 yn xn

24、 Xn-1,输入Sn是确定，f信号Sn=bn, b是常数。nn是白噪序列，零均2值，方差为n。求(i )输出中的信号分量；(ii)输出中噪声分量的均方和方差；(iii)输出中噪声分量的功率谱。解答：(i )输出中的信号分量yn Xn Xn-1 Sn hn Sn 15 1 bn bn 155 1前两项是由于信号S引起的输出，后面两项是噪声分量引起的输出。(ii)输出中噪声分量的均方和方差Enn nn 1 0,因此输出中噪声分量的均方等:于方差：2 2 2E(nn nn 1) Enn %-12/%-1(iii)输出中噪声分量的功率谱Pn(ej )1jj由于 H(z) 1 z ，则 H(ej ) 1

25、 e j_. j .-,j-2_,j一Pnoise(e )H(e ) Pn(e )口(2 2cos )2.对于上图中的系统模型，假设h (n)是因果的，用相关函数法推导出维纳滤波器的维纳一霍夫方程的离散形式，以及从该方程中解出了最佳滤波器hopt(n)后的最小均方误差的最简式。解答：h(n) 0,当 ny(n) ?(n) h(m)x(nu,m 02m) E e (n)E (s(n) h(m)x(n m)2m 02E (s(n) hopt(m)x(n m)x(n j) 0 j 0,1,2 m 0E s(n)x(n j) h°pt(m)Ex(n m)x(n j)m 0Rxs(j)hopt

26、(m)Rxx(j m) j 0维纳-霍夫万程：m 0最小均方误差为:22E e (n) min E (s(n) h°pt (m)x(n m)m 0E s2 (n) 2s(n)h(m)x(nm 0m) hopt(m)x(n m)h°pt(r)x(n r) m 0 r 0Rss(0) 2mhopt(m)Rxs(m)0hopt (m)hopt (r)Rxx(m r)m 0r 02 ，Ee (n)minRss(0)hopt (m)Rxs(m)m 03.设线性系统如上图所示，已知Snnn相互独立，且Ss(e)sin2Sn(ej )12 。要求设计个滤波器H(ej)csin2，试确定C

27、使得滤波后的输出?n与真实信号sn的均方误差最小，即E(sn sn)2最小。解答:设误差为en sn ?n其自相关为：Re(m)E(enenm)E( sn?n )(sn mSnm)Rs(m)Rs?(m)R?s(m)R?(m)做傅立叶变化：Se* ) Ss(ej ) Ss?(ej ) S，(ej )S?(ej )221S?(ej )H(ej)Sx(ej)H(ej)Ss(ej)Sn(ej)c2sin6 c2sin42Ss?(ej ) H(ei )Ssx(ei ) H(ei )Ss(ei ) csin4Sss(ej ) H (ei )Sxs(ei ) H (ei )Ss(ei ) csin4131

28、2c c2423copt一求导等于零：44.x(n)是白噪过程，零均值，方差为2x ,把x(n)作为输入加到一线性系统上，系统的冲激响应是h(n),输出是y(n)。证明:_2Ex(n)y(n)xh(0)(ii)解答:222 / 、y x h (n)n -Ex(n)y(n) Ex(n) x(n mh(m)Ex(n)x(n m) mh(m)Rx(m) mm)h(m)2当m=0时，Rx(。)x,当m为其匕时Rx(m) °,代入上式,_2Ex(n)y(n)xh(0)yEynynE h(m)x(n m) h(k)x(n k)h(m)h(k)Ex(nm km)x(n k)h(m)h(k)Rx(m

29、k)当 m=k 时，Rx (m k)当m为其它时Rx(m-k)0，代入上式,X h2(n)n -得证。第六章卡尔曼滤波1.有一信号s(n),其自相关函数Rs(m) 0.7m，m 0，1，2,被一零均值，方差为0.4的白噪n(n)所 淹没，s(n)与n(n)统计独立。2,(i)设计一个长度等于3的FIR数字滤波器，其输出 y(n)使得E(y(n)s(n)最小化。(ii)设计一个因果的最优滤波器，并说明如何在计算机上实现。解答：(i )根据均方误差最小准则得到W-H方程：N 1Rxs(j)hopt(m)Rxx(j m) j 01.2, ,N 1m 0，其中x=s+n,表不输入信号，n(n)s(n

30、m) Rs(m),代入 W-H 方程得:因为 N=3 ,且 Rxx(m) Rs(m) Rn(m),Rxs(m) Ex(n)s(n m) E(s(n)2Rs(j)hopt(m)Rs(j m) Rn(j m) j 0,1,2m 0把 Rs(m) 07 mLm 0, 1, 2,Rn(m)0.4 (m)代入上式得三个方程:2-mj 0:1 hopt (m)0.7' 1 0.4 ( m)m 021-mlj 1:0.7 hopt (m)0.7 1 0.4 (1- m)m 02._222-m-j 2:0.7 hopt (m)0.7'0.4 (2- m)m 021.40.70.72hopt(0

31、)10.71.40.7hopt(1)0.70.720.71.4hopt(2)0.720.61210.16810.0517hopt(0) hopt(1) 解得：hopt1-2所以设计的滤波器的传递函数为：H(Z) 0.6121 0.1681z0.0517z(ii)设计一个因果的最优滤波器因为 Rxx(m) Rs(m) Rn(m)所以输入信号的z变换为:Rxx(z)Rs(z) Rn(z)1.1060-0.28z-1 -0.28zI 1 I(1 0.7z )(1 0.7z)0.51I 1 I(1 0.7z )(1 0.7z)b(1 az 1 )(1 az)I 1 I(1 0.7z )(1 0.7z)

32、0.4b aO28 1.1060列出方程求系数 a与b,ab °，28利用solve函数解出a, b：a=3.68 , 0.2718 , b=0.76 ,1.03, a取小于 1 的数，所以 a=0.2718, b=1.03_1_1.03(1 0.2718z )(1 0.2718z)Rxx(Z)t-因此(1 0.7z )(1 0.7z)1、B (1 。/物)B -i(1 0.2718z)2B(Z)1 B(z )则 w 1.03,(1 0.7z 1),(1 0.7z)Rxs(z)/B(z1)2 _Hopt(z)wiB(z)Rs(z)/B(z 1)1 0.7z 10.512wT B( z

33、)1.03(1 0.2718z 1) (1 0.7z 1)(1 0.2718z)1 0.7z 10.62981.03(1 0.2718z1) (1 0.7z 1)0.62981.03(1 0.2718z1)h0Pt (n) 0.6115(0.2718)nu(n)2 / 、.E e (n) min计算机实现可以利用均方误差均方误差非常接近时就可以确定N 了。N 1Rss(0)hopt(m)Rss(m)m 0,当取N与N+1时它们的2 .比较维纳滤波和卡尔曼滤波方法的区别和联系。解答：维纳滤波和卡尔曼滤波都是解决线性滤波和预测问题的方法，并且都是以均方误差最小为准则的，在平稳条件下两者的稳态结果是

34、一致的。但是它们解决问题的方法有很大区别。维纳滤波是根据全部过去观测值和当前观测值来估计信号的当前值，因此它的解形式是系统的传递函数H (z)或单位脉冲响应h(n);卡尔曼滤波是用当前一个估计值和最近一个观测值来估计信号的当前值，它的解形式是状态变量值。维纳滤波只适用于平稳随机过程，卡尔曼滤波就没有这个限制。设计维纳滤波器 要求已知信号与噪声的相关函数，设计卡尔曼滤波要求已知状态方程和量测方程，当然两者之间也 有联系。3 .写出卡尔曼滤波的状态方程与量测方程，并解释。画出卡尔曼滤波的信号模型。解答：状态方程：S(k) A(k)S(k 1) wi(k 1)表示的含义就是在 k时刻的状态S(k)可

35、以由它的前一个时刻的状态S(k 曲来求得，即认为 k-1时刻以前的各状态都已记忆在状态S(k 1)中了。量测方程：X(k) C(k)S(k) w(k)用X(k)表示量测到的信号矢量序列，w(k)表示量测时引入的误差矢量，C(k) 称为量测矩阵，它的引入原因是，量测矢量 X(k)的维数不一定与状态矢量S(k)的维数相同，因为我们不一定能观测到所有需要的状态参数。卡尔曼滤波的信号模型:w(k)w1(k)*X(k)4.根据卡尔曼滤波的状态方程和量测方程，假设A(k)和C(k)是已知的，X(k) 是观测到的数据，也是已知的，假设信号的上一个估计值S(k D已知，如何来求当前时刻的估计值S(k) ?解答

36、：S(k) A(k)S(k 1) w1(k 1), X(k) C(k)S(k) w(k)假设暂不考虑w1(k)与w(k),用上两式得到的S?(k)和X(k)分别用S (k)和文(k)表示，得：S?(k) A(k) S(k 1)又(k)C(k)S?(k) C(k)A(k) 6(k1)必然，观测值X(k)和估计值X (k)之间有误差，它们之间的差 X(k)称为新息(innovation):X(k) X(k)又(k)新息的产生是由于我们前面忽略了w1(k)与w(k)所引起的，也就是说新息里面包含了w1(k)与w(k)的信息成分。因而我们用新息X(k)乘以一个修正矩阵H(k),用它来代替式的w1(k)

37、来对S(k)进行估计:S(k) A(k) S(k 1)H(k) X(k)A(k) S(k 1) H(K)X(k)C(k)A(k) S(k 1)S(k) A(k)S(k 1) H(K)C(k)S (k)w(k) C(k)A(k) S?(k 1)A(k)S(k 1) H(K)C(k) A(k) S(k 1) W1(k 1) w(k) C(k)A(k) S(k 1)A(k) S(k 1)IH(k)C(k) H(K)C(k)A (k) S(k 1) w1(k 1) H(k)w(k)根据上式来求最小均方误差下的H(k),然后把求到的H(k)代回去则可以彳#到估计值&k)。第七章参数滤波1 .对于

38、一个随机信号，可以对它进行频谱分析，叙述AR谱法和周期图法相比的优点。解答：平滑、需要较短数据即可、频率分辨率高、峰值包络线的好估计等。,一 14 m3 mRs(m)(0.81 ') (0.4叫),m Q 1, 22 .设已知1111，用L-D算法为此信号估计 p=1, 2, 3阶AR模型的系数和激励白噪的功率。解答：143Rs(0)1计算自相关函数：11 11_143Rs(1) 140.8 0.4 0.9091 1111143Rs(2)0.640.16 0.77091111143Rs(3)0.5120.064 0.63421111,下面为了简写，省略下标 So按照L-D算法得初始功率

39、和系数为：E0Rs(0) 1,a01d(1)R(1)/Eo 0.9091EiEo1 a：(1) 0.1736P=l :.R(2) &(1)R(1), _a2(2)0.32Ei a2 a1(1)1 a2(2)1.2_2 _ ._P=2: E2 E11 a2 (2) 0.1558a3（3）R（3） a2（1）R（2） a2（2）R（1）a3（1）a2（1）a3（2） a2（2）E2a3（3）a2（2）a3（3）a2（1）1.20.32P=3: E2E41 a2（2） 0.15583.某随机过程用AR模型拟和的结果是H（z）112343.5z4.58z2.6z0.58z ，试由它导出一个AR

40、MA解答：（2,1)模型。B（z）HARMA （z）设A（z）1 b1z 1Y121a1Za2Z要使得它与H (z)相等则有1 b1Z 1-1工1 &z a?z列出各系数方程:112341 3.5z4.58z2.6z0.58z“ 3.5 a1 b13.5 4.58 2.6 4.58bl 0.58 2.6b1 0.58b10a20利用后三个方程，最小二乘法解出“来，然后再利用前两个方程求出a1, a24.582.6e12.6 b10.58e20.580e3b1二 0.4779,两边同乘以4.58 2.6 0.58得伪逆解所以 &=3.0221 , a2=2.9074ARMA （2

41、, 1）模型为:,1H 1 0.4779zH ARMA （Z）121 3.0221Z2.9074Z4.如何用MATLAB 实现对一段脑电数据的AR 建模？该段数据如下1.719 0.743-0.722-2.187-2.187-1.2110.2540.7430.7430.2540.2540.7431.7191.231-0.234-2.187-3.652-3.164-1.2111.2312.2071.231-0.722-1.699-2.187-0.7220.2541.2310.743-0.234-1.699-3.164-4.14-5.117-5.605-5.117-3.652-2.187-1.21

42、1-1.211-2.187-4.14-5.117-5.117-4.14-3.164-2.675-2.675-2.675-3.164-3.164-3.164-2.675-2.187-1.699-1.211-1.211-1.699-2.187-2.187-2.187-2.187-2.187-1.699-1.211-0.2340.254-0.234-1.699-2.675-3.652-2.675-1.2110.2540.254-0.722-1.699-2.187-2.675-2.675-3.164-3.652-3.164-2.187-0.722-0.234-0.722-2.187-2.675-2.6

43、75-1.699-0.722-0.722-1.211-0.7220.2541.2311.231-0.234-2.675-4.628-4.628-2.675-0.2341.2310.743-0.234-1.699-1.699-2.187-2.187-2.187-2.187-1.699-0.722-0.722-1.211-1.211-1.699-1.699-1.699-2.187-2.675-4.14-4.14-3.164-1.699-1.699-3.164-4.628-5.117-4.628-3.652-2.187-1.699-2.187-2.187-2.187-1.211-0.2340.254

44、-0.234-0.722-1.699-2.187-2.187-2.187-0.7220.7431.7191.7190.743-0.722-0.722-0.7220.2541.2310.254-0.234-1.211-1.211-0.7220.2541.2311.2310.743-0.722-2.675-3.652-4.14-3.652-2.187-0.7220.7431.7192.2072.2072.2071.7191.2311.2311.2311.7192.2071.7190.743-0.722-2.187-2.675-2.187-1.211-0.234-0.234-1.699-3.164-

45、3.652-3.164-1.699-0.2340.7430.7430.254-0.722-1.211-1.211-0.722-0.2340.2540.2540.2540.7431.2311.7192.6962.6962.2070.743-0.722-1.211-0.7220.2540.2540.2540.254-0.234-0.2340.254-0.234-1.211-1.699-1.699-0.7220.2540.7430.254-1.211-2.187-2.187-1.211-0.2340.7430.7430.2540.2540.2540.254-0.234-0.234-1.211-1.2

46、11-0.722-0.2340.7431.2311.2310.254解答：在 MATLAB 中有专门的函数实现AR 模型的参数估计：a E=aryule( x， p) ，输入 x 表示观察信号，p 表示建模的阶数，输出 a 表示估计的参数，E 表示噪声信号的估计方差。也可以用arburg 函数实现AR 模型参数估计。代入本题的数据后可以得到：b e=aryule(a,5)b =1.0000-1.69690.88400.2906-0.46800.0464 e =0.2592b e=aryule(x,10)b =1.0000-1.66780.75930.4191-0.2989-0.2764-0.0

47、469-0.22110.0906e =0.23730.00590.2789第八章自适应信号处理1 .画出自适应噪声抵消的框图，并证明滤波后的输出将在最小均方意义下抵消噪声，同时，抵消后 的结果将在最小均方意义下逼进信号。解答：因为 E(s(n) e(n)2 E(y(n) n(n)2E(s(n) e(n)2E(s(n)2 E(e(n)2 2E(s(n)e(n)_2_2 E(s(n)E(e(n)2E(s(n)n(n) 2E(y(n)s(n)一2 _2E(s(n)E(e(n)框图:所以当均方误差最小时，s与e最逼近，同时y与n也最逼近。即滤波后的输出 y将在最小均方意义 下抵消噪声n,同时，抵消后的

48、结果 e将在最小均方意义下逼进信号so2 .列举自适应信号处理在生物医学信号处理中的部分应用。解答：自适应噪声抵消：例如母腹电极上胎儿心电的提取，心电图中工频干扰的抑制，心电图中高频手术 刀干扰的去除，呼吸阻抗中心电伪迹的消除等。自适应谱线增强：诱发脑电的提取等。自适应系统辨识：血压与血管收缩药物之间的系统自适应控制等。3 .简述横向结构的随机梯度法算法步骤。解答：步骤 1 观察到 P个值 X(T) Xt,Xt-1,Xt-2, Xt-pi步骤2：计算W(T 1) W(T) 2 eTX(T),初值W与eT预先给出，先给定。当有新观测值xT 1后，令X(T 1) xT1,xT, xTp2步骤3.计

49、算新的误差：eT 1 dT 1 W(T 1) X(T 1)转入步骤2,代入得到 W (T+2), e (T+2).使得W接近最优解。停止循环的判断规则多样。生物医学信号处理试卷集试卷：一、假设有两个离散平稳随机过程x,y(n), Rx(m) 0.6m , Ry(m) 08m它们统计独立，求这两个随机过程的乘积的自相关函数和功率谱密度。(14分)一j 、1j2 Sn(e )二、设线性系统如图所不，已知Sn,nn相互独立，且Ss(e ) Sin ,2。要求设计-个滤波器H (ej ) csin2 ，试确定C使得滤波后的输出 ?n与真实信号sn的均方误差最小，即E(sn ?n)最小。(14 分)x(n) s(n) n(n)y(n) s(n) h(n) 三、简述横向结构的随机梯度法算法步骤。(14 分)A(p) 四、利用A(p 1)(p)0A(p 1)Anv 推导L-D算法来解Y-W方程:p 20 Rxx(