角动量守恒定律

1、Nanjing University of Information Science & Technology第四章角动量守恒定律OHE 4主讲：陈玉林OSI 叵 1第四章角动量守恒定律§4-1力矩§ 4-2质点角动量守恒定律§4-3质点系角动量守恒定律§ 4-1 力 矩(moment of force)一.力矩的一般意义力臂定义：Af =r -X. F方向：垂直于F和戶组成的平面，服从右手定则。yX大小:M = Fr si n8 =如果作用于质点上的力是多个力的合力，即F =F+F_>+ + F “代入力矩定义中，得AZ = F x F =

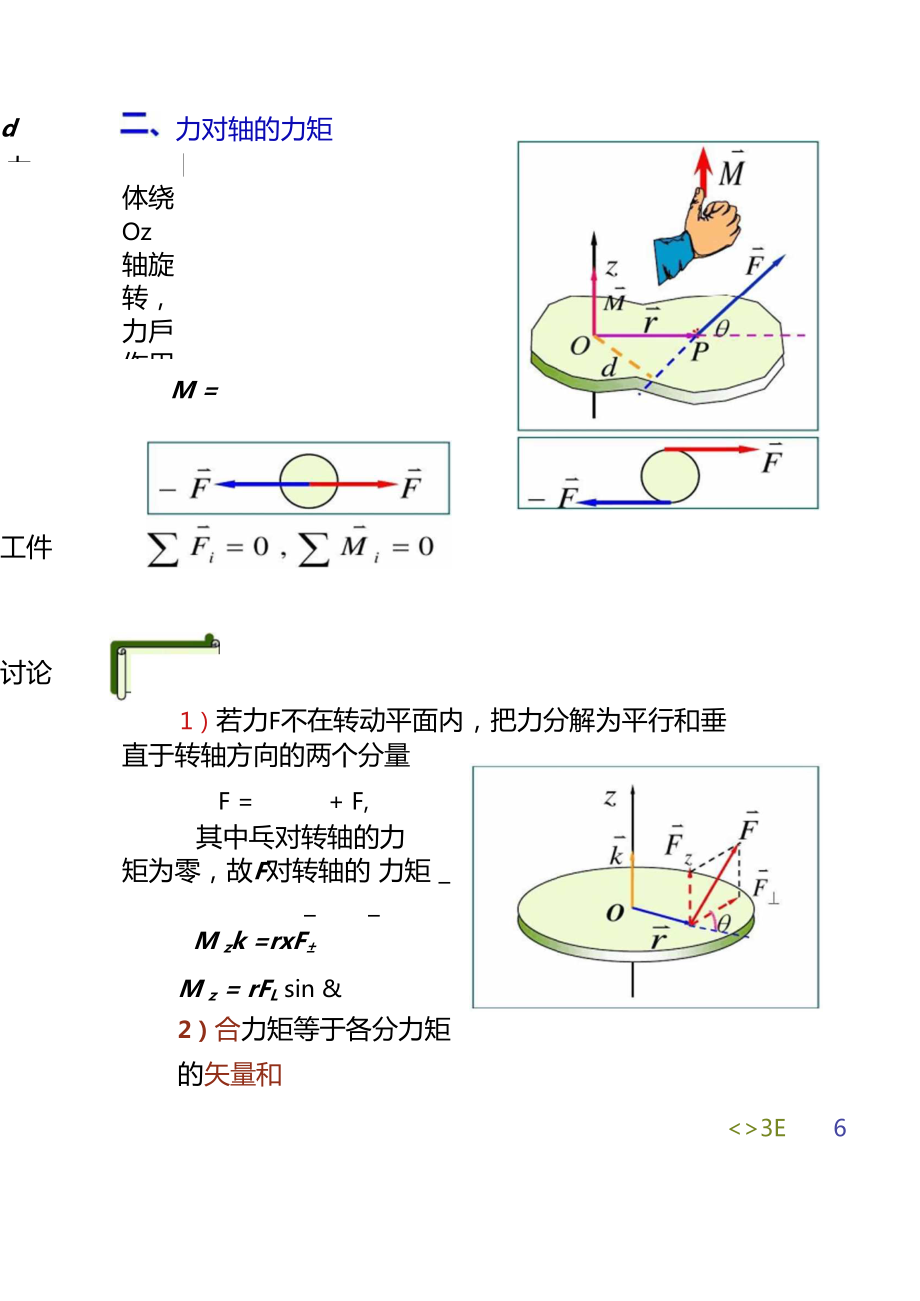
2、 r x (巧 + 尸2 1-尸)= FxP +F xF rx:FAf, + hf可见，合力对某参考点0的力矩等于各分力对同 一点力矩的矢量和。力对轴的力矩刚体绕Oz轴旋转，力戶 作用在刚体上点P,且在转动 平面内，为由点O到力的 作用点P的径矢 P对转轴Z的力矩_M = r x FM = Fr sin 0 = Fdd :力臂工件=0 ,工MhO讨论1）若力F不在转动平面内，把力分解为平行和垂 直于转轴方向的两个分量F =+ F,其中乓对转轴的力 矩为零，故F对转轴的 力矩 _M zk =rxF±M z = rFL sin & 2）合力矩等于各分力矩的矢量和M = M| +

3、M. + M： +1X<>3E63）刚体内作用力和反作用力的力矩互相抵消O3IE 8eraiF 7思考.合力为零时，其合力矩是否一定为零？ 1匸 合力矩为零时，合力是否一定为零？ J定由图可知，作用力和反作用力 对同一参考点合力矩为零. 从而，庆点系内力矩矢量和 一定为零.工E内=0工斤H0,工亿=0r = xi + yj zk , F<口口 Q在以参考点O为原点的直角坐标系中，M表示为 M = M f M 方 + M 工 质点戸的位置矢量F和作用力F可表示为=Fxi + Fyj + Fzkj ky zM = yF 乙 F 1 X丿乙，I分量式 M y = zFx -xFzM

4、z =xFyyF力矩沿某坐标轴的分量通常称作力对该轴的力矩。下面计算力对Z轴的力矩由图可见x = 7?cos a y = Rsin aFx = /cos pFx = /sin 0代入他式中可得imN證.OHIE io力对Z轴的力矩M r = Rf (cos<zsin ft sinzcos /?)=Rf sin(0 cx)= Rf sin 0 式中/?、f为F、F在刊平面上 的投影。Q如果知道力矩矢量的大小和 它与z轴之间的夹角y,那么力 对z轴的力矩也可按下式求得M = M cos y=r F sin & cos y§4.2质点角动量守恒定律 角动量(angular m

5、omentum) 质点加对O点的角动量：质量为m的质点以速度方 在空间运动，某时刻相对原点 O的位矢为已质点相对于原 点的角动量定义为I =rxp=rxmv 大小 I =rmvsin0 方向右手螺旋定则判定 单位 kgm2/s<口匸 11说一个角动畳肘，必须指明旻对呷个固走点而言的。质点对通过参考点O的任意轴线Oz的角动量4,是 质点相对于同一参考点的角动量2沿该轴线的分量。= cos x如果质点始终在Oxy平面上运动, 质点对4轴的角动量与对参考点0 的角动量的大小是相等的，即I = I = rmv sinZmvX注意面对z轴观察，由产方向沿逆时针转向mv的方L = rp = tnrv

6、 = tnr 2a)向所形成的角才是&角。、滋T 一质量为加的质点沿着一条空间曲线运动， 寇曲线在直角坐标下的矢径为：产- a cos a)ti 4- b sin cotj 其中4. b. 0皆为常数，求该质点对原点的角动量。解：已知 r =a coscMi 4-bsinotj_ drv = acDslYa)ti -fbcocoscatjd/角动量-_22l =r x z/iv =mabcocoscotk 4-cotk = mabcokOH1E 15二.角动量定理(theorem of angular momentum) 牛顿定律T角动量定理：角动量r =y X p 9两边求导d7 d

7、 _二一 一一(r xp)-rx+x p - r x F + vx/nvdt Atdt dt|!匚二1共线，叉乘为零牛二定律：虔=司din作用于质点的合力对参考点oM =的力矩，等于质点对该点o的角i1I动量随时间的变化率.角动套定理因是牛顿定律的推论，则只适用于惯性系。Gi 面 口 1 &历3dt-MAt = d/fMdt = i2-Tl1称为冲量矩质点的角动量定理：对同一参考点O f质点所 受的冲量矩等于质点角动量的增量.角动量定理的分量形式如果质点始终在巧平面上运动，可得到陆dl/f = (rmv sin 0) 必z dtOH1E 16三.质点角动量守恒定律a 1由角动量定律d

8、iM =>dtI =恒矢量即7、=72=恒矢量若对惯性糸禁一固走点，质点所受的合外力 矩为零,则此质盍对该固走点的角动量矣董锋 持不变，即角动量的丸小和方向都傑持不jt。和动量守恒定律一样，角动量守恒定律也是自然界的一条最基本的定律。注意：M =0 可以是F-Of也可以是亓=0.还可能是戸与亓 同向或反向"例如有心力情况。如果作用于质点的合力矩不为零而合力矩沿OZ轴的分量为零，则I =恒量（当M0时）ZZ当质点所受对6轴的力矩为零时，质点对该轴 的角动量保持不变。此结论称为质点对轴的角动量 社定律。O3IE is()$3 开普勒第二定律认为：对于任一行星，由太 阳到行星的矢径在

9、相等的时间内扫过相等的面积。 试用角动量守恒定律证明。解：将行星看为质点，在dz时间内以速度0完成的位移为ydt 矢径产在 d/时间内扫过的面积为dS （图中阴影！ds = r x vdt,2 _根据质点角动量的定义I = r x mv = m(r x v ) Zds Ids =dt zz=2mdt 2m恥丄=恒量.2m口匸 1Q行星受万有引力，为有心力，SA7=0, 7 =恒矢量&砂质量为加的小球系于细绳的一端，绳的另一 端缚在一根竖直放置的细棒上，小球被约束在水平面 内绕细棒旋转，某时刻角速度为细绳的长度为口。 当旋转了若干圈后，由于细绳缠绕在细棒上，绳长变 为2,求此时小球绕细棒

10、旋转的角速度畋。解：小球受力 绳子的张力几指向细棒； 重力巧竖直向下；支撑力了竖直向上。，亍与绳子平行，不产生力矩；斤与W 平衡，力矩始终为零。所以，作用于小 球的力对细棒的力矩始终等于零，故小 球对细棒的角动量必定是守恒的。O3E 21根据质点对轴的角动量守恒定律mVj rx = mvr式中勺是半径为口时小球的线速:度，也是半径为 勺时小球的线速度。而 V1 =叫G， v2 =吟2代入上式得2 2co = rnr <»2解得2 =（ ）2«!r2可见，由于细绳越转越短，° < 口，小球的角速度 必定越转越大，即Q 2 >。I。环置于竖直平面内一

11、质量为 加的小球穿在圆环上，并可在圆环上滑动小球开始时 静止于圆环上的点4 （该点在通过环心O的水平面上）， 然后从4点开始下滑设小球与圆环间的摩擦略去不计.求小球滑到点B时对环心O的角动量和角速度.解小球受重力和支持 力作用，支持力的力矩为零, 重力矩垂直纸面向里M = mgR cos 6由质点的角动量定理dLmgR cos 0 =OSIEdrdLmgR cos 0 =dtdL = mgR cos 0dt考虑到co = d0/df, L = mR v = mR a> 得 LdL = mgR 3 cos 0d0 由题设条件积分上式LdL = m gR 3 f cosJoJoL = mR

12、3/2 (2g sin )，/2 本题也可以用质点的功能原理求解. L = mR 2co/2gq、1/2cd = sin 6 )R*§4-3质点系角动量守恒走律一.质点系的角动量走理设质点系有个质点组成质量加I，叫,，®速度V, , v2, n位矢斤，产2,壬力矩质点系的角动量为所有质点的角动量的矢量之和Ji/f乙=W町=兀O3E 25对每个质点，根据角动量定理列方程:心=，忌=d/drO3E 27个方程相加M + M 步 + Af产忆+ A+ +乙）d/考虑质点间的相互作用dLdt工竹外+工M内因为艺必内=0 直接表示为一 d L牙M =厶d/质点系的角动量定理表述：一个质点糸所受的合外力矩，等于该质点 糸的总角动量对对间的变化率二.质点系角动量守恒定律当工启=o时 Z =恒矢量