线性回归分析的基本步骤

1、步骤一、建立模型知识点：1、总体回归模型、总体回归方程、样本回归模型、样本回归方程 总体回归模型：研究总体之中自变量和因变量之间某种非确定依赖关系 的计量模型。Y = X 1 U特点：由于随机误差项 U的存在，使得 Y和X不在一条直线/平面上。例1:某镇共有60个家庭，经普查，60个家庭的每周收入（X）与每周 消费（Y）数据如下：每周收入（X）每周消费支出（Y）8055606570751006570748085881207984909498140809395103108113115160102107110116118125180110115120130135140200120136140144

2、145220135137140152157160162240137145155165175189260150152175178180185191作出其散点图如下:200180160140Y 1201008060404080120160200240280X 总体回归方程（线）：由于假定EU = 0，因此因变量的均值与自变量总处于一条直线上，这条直线E Y|X = Xi就称为总体回归线（方程） 总体回归方程的求法：以例 1的数据为例1）对第一个Xi，求出E（YXi）每周收入（X）每周消费支出（Y）E(Y|Xi)80556065707565100657074808588771207984909498

3、89140809395103108113115101160102107110116118125113180110115120130135140125200120136140144145137220135137140152157160162149240137145155165175189161260150152175178180185191173由于E Yj|Xj = "Xj，因此任意带入两个Xi和其对应的E（Y|Xi）值，即可求出飞和，并进而得到总体回归方程。如 将 X 100,E Y2 |X2 = 77和X 200,E Y7 | X7 = 137 代 入E 丫 |Xj 0Xi 可得

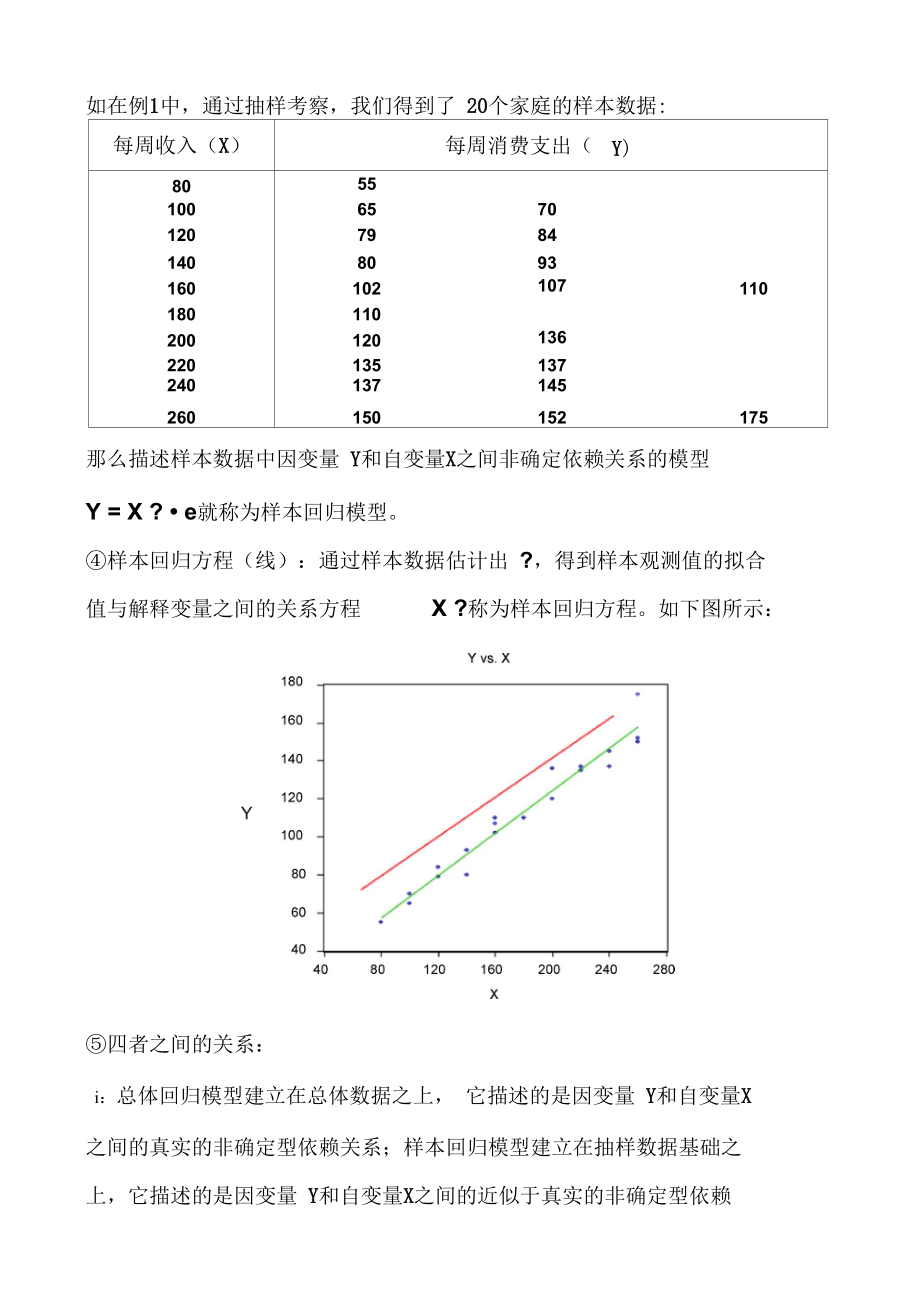
4、:77 = 0 100 一 。= 17 137=0200 “厂 0.6以上求出s和：1反映了 E（Y|Xi）和Xi之间的真实关系，即所求的总体回归 方程为：E Yi |Xi - 17 06Xi，其图形为：样本回归模型：总体通常难以得到，因此只能通过抽样得到样本数据。如在例1中，通过抽样考察，我们得到了 20个家庭的样本数据:每周收入（X）每周消费支出（Y)8055100657012079841408093160102107110180110200120136220135137240137145260150152175那么描述样本数据中因变量 Y和自变量X之间非确定依赖关系的模型Y = X ?

5、e就称为样本回归模型。样本回归方程（线）：通过样本数据估计出 ?，得到样本观测值的拟合 值与解释变量之间的关系方程X ?称为样本回归方程。如下图所示：四者之间的关系：i：总体回归模型建立在总体数据之上， 它描述的是因变量 Y和自变量X之间的真实的非确定型依赖关系；样本回归模型建立在抽样数据基础之上，它描述的是因变量 Y和自变量X之间的近似于真实的非确定型依赖关系。这种近似表现在两个方面：一是结构参数?是其真实值1的一种近似估计；二是残差 e是随机误差项u的一个近似估计；丘：总体回归方程是根据总体数据得到的，它描述的是因变量的条件均值E(Y|X)与自变量X之间的线性关系；样本回归方程是根据抽样数

6、据得到 的，它描述的是因变量 Y样本预测值的拟合值Y?与自变量X之间的线性 关系。iii：回归分析的目的是试图通过样本数据得到真实结构参数 1的估计值， 并要求估计结果?足够接近真实值1。由于抽样数据有多种可能，每一 次抽样所得到的估计值 ?都不会相同，即1的估计量?是一个随机变量。 因此必须选择合适的参数估计方法，使其具有良好的统计性质。2、随机误差项U存在的原因： 非重要解释变量的省略 人的随机行为 数学模型形式欠妥 归并误差(如一国GDP的计算) 测量误差等3、多元回归模型的基本假定 随机误差项的期望值为零 E(UiH 0 随机误差项具有同方差性 Var(uJ2 i = 1,2,|,n

7、随机误差项彼此之间不相关 Cov(uUj) = 0 i = j ; i, j = 1,2,|,n 解释就变量x1?x2, -,Xk为确定型变量，与随机误差项彼此不相关。Cov(Xij,Ujp 0 i 二 1,2jll,kj = 1,2jll,n 解释就变量X1,X2, -；xk之间不存在精确的（完全的）线性关系，即解 释变量的样本观测值矩阵 X为满秩矩阵：rank（X）=k+1<n 随机误差项服从正态分布，即：UjN（0,；2），i=1,2,訓步骤二、参数估计知识点：1、最小二乘估计的基本原理：残差平方和最小化。2、参数估计量：'? 乞Xi严12 一元回归：<送XiW陆X

8、多元回归：?= X X 1 xty3、最小二乘估计量的性质（Gauss-Markov定理）：在满足基本假设的情况下，最小二乘估计量?是：的最优线性无偏估 计量（BLUE估计量）步骤三、模型检验1、经济计量检验（后三章内容）2、统计检验拟合优度检验知识点：i：拟合优度检验的作用：检验回归方程对样本点的拟合程度ii：拟合优度的检验方法：计算（调整的）样本可决系数R2/R2r2毕十彈,R2十ESS/n k1TSS TSS 'TSS/n 1注意掌握离差平方和、回归平方和、残差平方和之间的关系以及它们的自由度。计算方法：通过方差分析表计算方差来源符号计算公式自由度（d.f.）均方值（MSS）离差

9、平方和TSS2 送(Yi -Y ) in-12E (Yi Y)/n-1 i回归平方和RSSZ (£-Y)2ik送(Y?-Y,/ki残差平方和ESSin-k-12送(¥ / n-k-1i例2:下表列出了三变量（二元）模型的回归结果:方差来源平方和（SS）自由度均方值离差平方和TSS6604214回归平方和RSS65965残差平方和ESS1）样本容量为多少？解：由于TSS的自由度为n-1，由上表知n-1 = 14,因此样本容量n=152）求 ESS解：由于 TSS= ESS+ RSS, 故 ESS= TSS RSS= 77 3） ESS和RSS的自由度各为多少？解：对三变量模型

10、而言， k=2，故ESS的自由度为n-k-1 = 12RSS的自由度为k= 24)求R2和R2解:R2RSSTSS6596566042二 0.9988 ,R2十需汁0.9986 回归方程的显著性检验（F检验）目的：检验模型中的因变量与自变量之间是否存在显著的线性关系步骤：1、提出假设：H 0 ： 1；- = -2 = .= 5 = 0H1 :至少有一目 j 式 0, j =1,2,., k2、构造统计量：F RSS/k F（k,n_k_1）ESS/n -k 13、 给定显著性水平，确定拒绝域F F k,n_k_14、计算统计量值，并判断是否拒绝原假设例3:就例2中的数据，给定显著性水平：一 1

11、%，对回归方程进行显著性检验。解：由于统计量值FRS659竺公"140.13，ESS/nk177/12又 F0.01 (2,12)=6.93，而 F =5140.13>F0.01 (2,12)= 6.93故拒绝原假设，即在1%的显著性水平下可以认为回归方程存在显著 的线性关系。附：R2与F检验的关系:,2 RSS RSSR2RRSS2 ESS_ 2 ,.由于 TSS ESS RSS1R2FR /kRSS/k 厂(1-R2 )/(n-k-1 )又ESS/nk1 J 解释变量的显著性检验（t检验） 目的：检验模型中的自变量是否对因变量存在显著影响。知识点:多元回归：Ss+，其中C3

12、为（XX）中位于第i+1行和i+1列的元素;一元回归:s?0Z eL Xi2Sn(nx2，SP变量显著性检验的基本步骤:1、提出假设：叫：片=0弭式02、构造统计量：t = = t(n - k-“ Sj?3、给定显著性水平，确定拒绝域t t：/2（n-k-1）4、计算统计量值，并判断是否拒绝原假设例4:根据19个样本数据得到某一回归方程如下：Y?二 58.9 0.2X“ 一 0.1X2se（0.0092） （0.084）试在5%的显著性水平下对变量 X,和X2的显著性进行检验。解：由于ta/2（n-k-1）=如25（16） = 2.12，故t检验的拒绝域为>2.12。对 自变量X1而言，

13、其t统计量值为0221.74 2.12，落入S?0.0092拒绝域，故拒绝 0的原假设，即在5%的显著性水平下，可以认为自变量X1对因变量有显著影响；对自变量X2而言，其t统计量值为t =磐=吕基=1.19< 2.12，未落入拒S?0.084绝域，故不能拒绝0的原假设，即在 5%的显著性水平下，可以认为自变量X2对因变量Y的影响并不显著。 回归系数的置信区间目的：给定某一置信水平1，构造某一回归参数 訂的一个置信区间，使i落在该区间内的概率为1 -:基本步骤:? _ R1、构造统计量i =-=t（n k1）S?2、给定置信水平1，查表求出：水平的双侧分位数t./2（n k1）3、求出&#

14、39;-i的置信度为1-的置信区间？-t：./2 S?,? t：./2 S?例5:根据例4的数据，求出:1的置信度为95%的置信区间。解：由于如25（16） = 2.12，故'-1的置信度为95%的置信区间为：0.2 2.12 0.0092,0.2 2.12 0.0092 二 0.18,0.223、经济意义检验目的：检验回归参数的符号及数值是否与经济理论的预期相符。例6:根据26个样本数据建立了以下回归方程用于解释美国居民的个人消费支出：Y?二 10.96 0.93X"2.09X2t （ 3.33） （249.06） （一3.09）R2 二 0.9996其中：Y为个人消费支出

15、（亿元）；X1为居民可支配收入（亿元）；X2为 利率（%）1）先验估计时和囤的符号；解：由于居民可支配收入越高，其个人消费水平也会越高，因此预期自变量X1回归系数的符号为正；而利率越高，居民储蓄意愿越强，消费意愿 相应越低，因此个从消费支出与利率应该存在负相关关系，即?2应为负。2）解释两个自变量回归系数的经济含义；解：弭=0.93表示，居民可支配收入每增加1亿元，其个人消费支出相应会增加0.93亿元，即居民的边际消费倾向MPC = 0.93；?22.09表示，利率提高1个百分点，个人消费支出将减少2.09亿元截距项表示居民可支配收入和利率为零时的个人消费支出为-10.96亿元，它没有明确的经

16、济含义。3）检验1是否显著不为1; （=5%）解：1）提出假设：H o ： 1=1已"2） 构造统计量：t = -? lt（nk1）S目3） 给定显著性水平:=5°%，查表得t：./2（n k 1）=如25（23） = 2.07，故拒绝 域为2.074） 计算统计量值：由于t（ ?1）' S?0930.003734S?* t（弭）249.06则|t| =0.07 =18.752.07，落入拒绝域。故拒绝 忆=1的原假设。S?0.003734即在5%的显著性水平下，可认为边际消费倾向 MPC显著不为1。4） 检验j显否显著不为零； O "%） 解：1）提出假

17、设：H0:"0 治2=0、翼2） 构造统计量：t=gt（n-k-1）s®3） 给定显著性水平:=5%，查表得t/2（n-k-1） = t0.025（23） = 2.07，故拒绝域为2.074） 计算统计量值：由于t（ ?2） = 3.09 2.07，落入拒绝域，故拒绝原假设。即在5%的显著性水平下，可以认为2显著异于零。5）计算R2值；R2解:由于ESS / n -k -1二 1 -TSS / n 1ESS n-1=1 一TSS n - k 一 12=1 - 1-R=1 - 1 -0.999626 126 2 1=0.999576) 计算每个回归系数的标准差;S?0 =解：

18、由于询二廿厂也_-3.330.93t(?)249.06JL.-2.090.00373S?1% t(罵厂-3.09?0W3.29=0.67647) 给出2置信水平为95%的置信区间;解：由于?2 = -2.09 , Sp =0.6764 , t°.025(23) = 2.07，故 氏置信水平为95%的置信区间为 -2.09-2.07 0.6764 , - 2.09 2.07 0.6764 二-3.49 , -0.698) 对回归方程进行显著性检验；解：提出假设：H0 :0 已或构造统计量RSS/kESS/nk-1 F (k,n -k -1)确定拒绝域： F iFJk.nk1) = Fo

19、.05(2,23) =3.42计算统计量并进行判断:R2/k1 -R2 / n -k -10.9996/20.0004/23二 28738.53.42故拒绝原假设，即在5%的显著性水平下认为回归方程的线性关系显 著成立。步骤四：经济预测点预测：Y?=X°?可以看着是Y的条件均值EY°|X0和个别值Y。的预测值， 分别称为均值预测和个值预测；性质：Y? =X0?是E Y°|X0和Y。的一个无偏估计量。区间预测：均值EY°|X0的区间预测预测步骤：1)确定统计量：t= 一E Y01 X0 t(n-kT)SY?其中Sy0冷二葺Xo(XXX00n -k -12)给定置信水平，确定