文科一轮学案111事件与概率

1、第十一章 概率学案11.1 事件与概率自主预习案 自主复习 夯实基础【双基梳理】1事件(1)不可能事件、必然事件、随机事件：在同样的条件下重复进行试验时，有的结果 ，它称为不可能事件；有的结果在每次试验中 ，它称为必然事件；有的结果 ，也 ，它称为随机事件(2)基本事件、基本事件空间：试验连同它出现的每一个结果称为一个基本事件，它是试验中不能再分的最简单的 ；所有基本事件 构成的 称为基本事件空间，基本事件空间常用大写希腊字母表示2概率与频率(1)概率定义：在n次重复进行的试验中，事件A发生的频率，当n很大时，总是在某个常数附近摆动，随着n的增加，摆动幅度越来越小，这时就把这个常数叫做事件A的

2、概率，记作P(A)(2)概率与频率的关系： 可以通过 来“测量”， 是 的一个近似3事件的关系与运算名称定义并事件(和事件)由事件A和B 所构成的事件C互斥事件不可能 的两个事件A、B互为对立事件不能 且 的两个事件A、B4.概率的几个基本性质(1)概率的取值范围： .(2)必然事件的概率：P(E) .(3)不可能事件的概率：P(F) .(4)互斥事件的概率加法公式：P(AB) (A，B互斥)P(A1A2An) (A1，A2，An彼此互斥)(5)对立事件的概率：P() 【知识拓展】互斥事件与对立事件的区别与联系互斥事件与对立事件都是两个事件的关系，互斥事件是不可能同时发生的两个事件，而对立事件

3、除要求这两个事件不同时发生外，还要求二者之一必须有一个发生，因此，对立事件是互斥事件的特殊情况，而互斥事件未必是对立事件【思考辨析】判断下面结论是否正确(请在括号中打“”或“×”)(1)事件发生频率与概率是相同的()(2)随机事件和随机试验是一回事()(3)在大量重复试验中，概率是频率的稳定值()(4)两个事件的和事件是指两个事件都得发生()(5)对立事件一定是互斥事件，互斥事件不一定是对立事件()(6)两互斥事件的概率和为1.()考点探究案 典例剖析 考点突破考点一 事件关系的判断例1某城市有甲、乙两种报纸供居民订阅，记事件A为“只订甲报纸”，事件B为“至少订一种报纸”，事件C为“

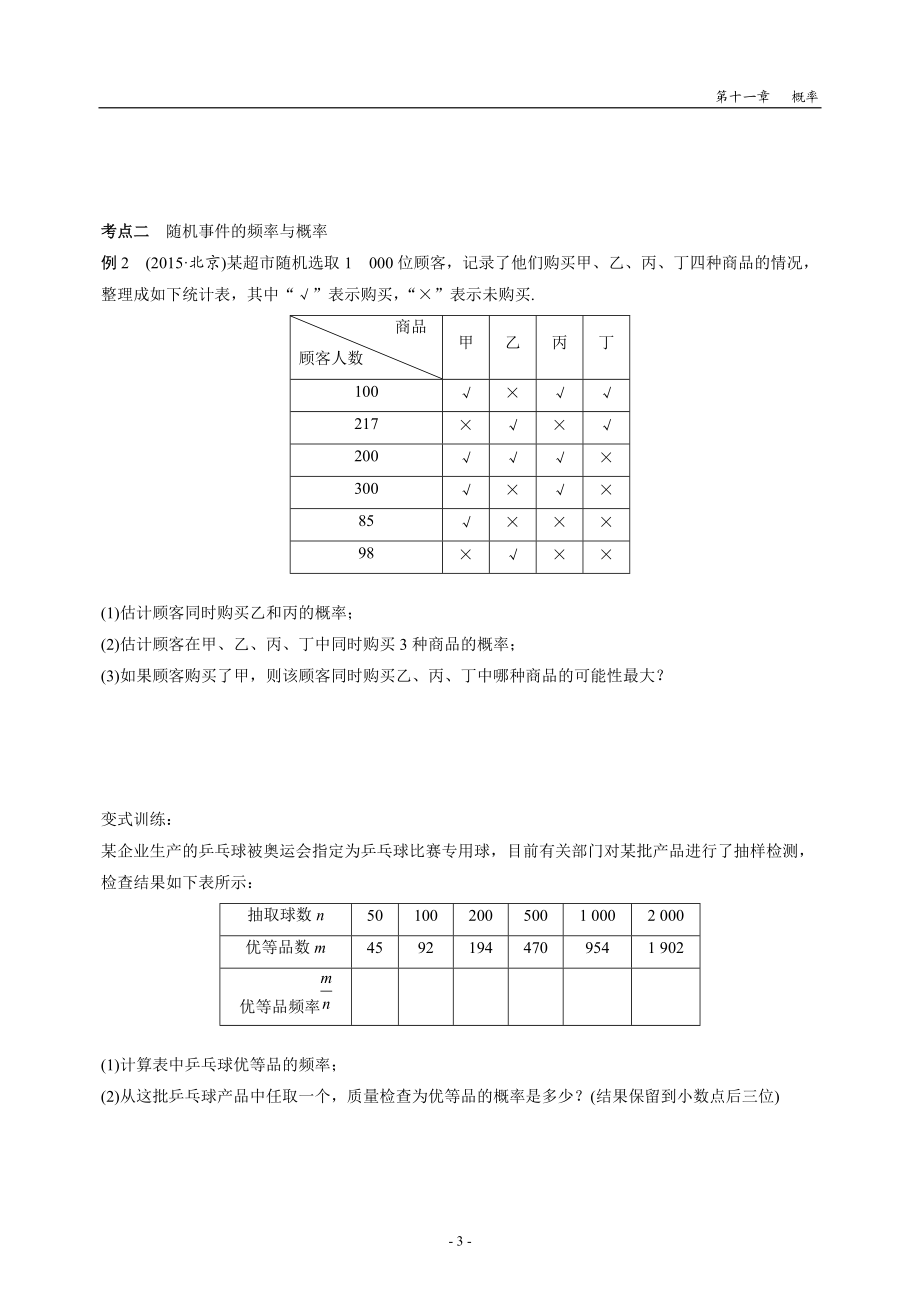
4、至多订一种报纸”，事件D为“不订甲报纸”，事件E为“一种报纸也不订”判断下列每对事件是不是互斥事件；如果是，再判断它们是不是对立事件(1)A与C；(2)B与E；(3)B与C；(4)C与E.变式训练：判断下列各对事件是不是互斥事件或对立事件：某小组有3名男生和2名女生，从中任选2名同学去参加演讲比赛，其中(1)恰有1名男生和恰有2名男生；(2)至少有1名男生和至少有1名女生；(3)至少有1名男生和全是女生 考点二 随机事件的频率与概率例2(2015·北京)某超市随机选取1 000位顾客，记录了他们购买甲、乙、丙、丁四种商品的情况，整理成如下统计表，其中“”表示购买，“×”表示

5、未购买. 商品顾客人数甲乙丙丁100×217××200×300××85×××98×××(1)估计顾客同时购买乙和丙的概率；(2)估计顾客在甲、乙、丙、丁中同时购买3种商品的概率；(3)如果顾客购买了甲，则该顾客同时购买乙、丙、丁中哪种商品的可能性最大？变式训练：某企业生产的乒乓球被奥运会指定为乒乓球比赛专用球，目前有关部门对某批产品进行了抽样检测，检查结果如下表所示：抽取球数n501002005001 0002 000优等品数m45921944709541 902优等品频率(

6、1)计算表中乒乓球优等品的频率；(2)从这批乒乓球产品中任取一个，质量检查为优等品的概率是多少？(结果保留到小数点后三位)考点三：互斥事件、对立事件的概率命题点1互斥事件的概率例3袋中有12个小球，分别为红球、黑球、黄球、绿球，从中任取一球，得到红球的概率是，得到黑球或黄球的概率是，得到黄球或绿球的概率也是，试求得到黑球、黄球和绿球的概率各是多少？命题点2对立事件的概率例4某商场有奖销售中，购满100元商品得1张奖券，多购多得.1 000张奖券为一个开奖单位，设特等奖1个，一等奖10个，二等奖50个设1张奖券中特等奖、一等奖、二等奖的事件分别为A、B、C，求：(1)P(A)，P(B)，P(C)

7、；(2)1张奖券的中奖概率；(3)1张奖券不中特等奖且不中一等奖的概率变式训练：国家射击队的队员为在射击世锦赛上取得优异成绩，正在加紧备战，经过近期训练，某队员射击一次命中710环的概率如下表所示：命中环数10环9环8环7环概率0.320.280.180.12求该射击队员射击一次：(1)射中9环或10环的概率；(2)命中不足8环的概率当堂达标：1一个人打靶时连续射击两次，事件“至少有一次中靶”的互斥事件是()A至多有一次中靶 B两次都中靶C只有一次中靶 D两次都不中靶2从某班学生中任意找出一人，如果该同学的身高小于160 cm的概率为0.2，该同学的身高在160,175(单位：cm)内的概率为

8、0.5，那么该同学的身高超过175 cm的概率为()A0.2 B0.3 C0.7 D0.83(2015·湖北)我国古代数学名著数书九章有“米谷粒分”题：粮仓开仓收粮，有人送来米1 534石，验得米内夹谷，抽样取米一把，数得254粒内夹谷28粒，则这批米内夹谷约为()A134石 B169石C338石 D1 365石4给出下列三个命题，其中正确的命题有_个有一大批产品，已知次品率为10%，从中任取100件，必有10件是次品；做7次抛硬币的试验，结果3次出现正面，因此正面出现的概率是；随机事件发生的频率就是这个随机事件发生的概率5(教材改编)袋中装有9个白球，2个红球，从中任取3个球，则恰

9、有1个红球和全是白球；至少有1个红球和全是白球；至少有1个红球和至少有2个白球；至少有1个白球和至少有1个红球在上述事件中，是对立事件的为_巩固提高案 日积月累 提高自我1下列命题：将一枚硬币抛两次，设事件M：“两次出现正面”，事件N：“只有一次出现反面”，则事件M与N互为对立事件；若事件A与B互为对立事件，则事件A与B为互斥事件；若事件A与B为互斥事件，则事件A与B互为对立事件；若事件A与B互为对立事件，则事件AB为必然事件，其中，真命题是()A BC D2围棋盒子中有多粒黑子和白子，已知从中取出2粒都是黑子的概率为，都是白子的概率是，则从中任意取出2粒恰好是同一色的概率是()A. B. C

10、. D13在5张电话卡中，有3张移动卡和2张联通卡，从中任取2张，若事件“2张全是移动卡”的概率是，那么概率是的事件是()A至多有一张移动卡 B恰有一张移动卡C都不是移动卡 D至少有一张移动卡4从存放的号码分别为1,2,3，10的卡片的盒子中，有放回地取100次，每次取一张卡片并记下号码，统计结果如下：卡片号码12345678910取到次数138576131810119则取到号码为奇数的卡片的频率是()A0.53 B0.5 C0.47 D0.375对一批产品的长度(单位：毫米)进行抽样检测，下图为检测结果的频率分布直方图根据标准，产品长度在区间20,25)上的为一等品，在区间15,20)和25

11、,30)上的为二等品，在区间10,15)和30,35)上的为三等品用频率估计概率，现从该批产品中随机抽取一件，则其为二等品的概率为()A0.09 B0.20 C0.25 D0.456在200件产品中，有192件一级品，8件二级品，则下列事件：在这200件产品中任意选出9件，全部是一级品；在这200件产品中任意选出9件，全部是二级品；在这200件产品中任意选出9件，不全是二级品其中_是必然事件；_是不可能事件；_是随机事件7已知某运动员每次投篮命中的概率都为40%，现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率：先由计算器产生0到9之间取整数值的随机数，指定1,2,3,4表示命中，5

12、,6,7,8,9,0表示不命中；再以每三个随机数为一组，代表三次投篮的结果经随机模拟产生了如下20组随机数：907966191925271932812458569683431257393027556488730113537989据此估计，该运动员三次投篮恰有两次命中的概率为_8若随机事件A，B互斥，A，B发生的概率均不等于0，且P(A)2a，P(B)4a5，则实数a的取值范围是_9(2014·陕西)某保险公司利用简单随机抽样方法，对投保车辆进行抽样，样本车辆中每辆车的赔付结果统计如下：赔付金额(元)01 0002 0003 0004 000车辆数(辆)500130100150120(

13、1)若每辆车的投保金额均为2 800元，估计赔付金额大于投保金额的概率；(2)在样本车辆中，车主是新司机的占10%，在赔付金额为4 000元的样本车辆中，车主是新司机的占20%，估计在已投保车辆中，新司机获赔金额为4 000元的概率10从某学校的800名男生中随机抽取50名测量其身高，被测学生身高全部介于155 cm和195 cm之间，将测量结果按如下方式分组：第一组155,160)，第二组160,165)，第八组190,195，如图是按上述分组方法得到的频率分布直方图的一部分，已知第一组与第八组人数相同，第六组的人数为4.(1)求第七组的频率；(2)估计该校的800名男生的身高的中位数以及身

14、高在180 cm以上(含180 cm)的人数；(3)若从身高属于第六组和第八组的所有男生中随机抽取两名男生，记他们的身高分别为x，y，事件E|xy|5，事件F|xy|>15，求P(EF)学案11.1 时间与概率自主预习案 自主复习 夯实基础【双基梳理】1事件(1)不可能事件、必然事件、随机事件：在同样的条件下重复进行试验时，有的结果始终不会发生，它称为不可能事件；有的结果在每次试验中一定会发生，它称为必然事件；有的结果可能发生，也可能不发生，它称为随机事件(2)基本事件、基本事件空间：试验连同它出现的每一个结果称为一个基本事件，它是试验中不能再分的最简单的随机事件；所有基本事件构成的集合

15、称为基本事件空间，基本事件空间常用大写希腊字母表示2概率与频率(1)概率定义：在n次重复进行的试验中，事件A发生的频率，当n很大时，总是在某个常数附近摆动，随着n的增加，摆动幅度越来越小，这时就把这个常数叫做事件A的概率，记作P(A)(2)概率与频率的关系：概率可以通过频率来“测量”，频率是概率的一个近似3事件的关系与运算名称定义并事件(和事件)由事件A和B至少有一个发生所构成的事件C互斥事件不可能同时发生的两个事件A、B互为对立事件不能同时发生且必有一个发生的两个事件A、B4.概率的几个基本性质(1)概率的取值范围：0P(A)1.(2)必然事件的概率：P(E)1.(3)不可能事件的概率：P(

16、F)0.(4)互斥事件的概率加法公式：P(AB)P(A)P(B)(A，B互斥)P(A1A2An)P(A1)P(A2)P(An)(A1，A2，An彼此互斥)(5)对立事件的概率：P()1P(A)【知识拓展】互斥事件与对立事件的区别与联系互斥事件与对立事件都是两个事件的关系，互斥事件是不可能同时发生的两个事件，而对立事件除要求这两个事件不同时发生外，还要求二者之一必须有一个发生，因此，对立事件是互斥事件的特殊情况，而互斥事件未必是对立事件【思考辨析】判断下面结论是否正确(请在括号中打“”或“×”)(1)事件发生频率与概率是相同的(×)(2)随机事件和随机试验是一回事(×

17、;)(3)在大量重复试验中，概率是频率的稳定值()(4)两个事件的和事件是指两个事件都得发生(×)(5)对立事件一定是互斥事件，互斥事件不一定是对立事件()(6)两互斥事件的概率和为1.(×)考点探究案 典例剖析 考点突破考点一 事件关系的判断例1某城市有甲、乙两种报纸供居民订阅，记事件A为“只订甲报纸”，事件B为“至少订一种报纸”，事件C为“至多订一种报纸”，事件D为“不订甲报纸”，事件E为“一种报纸也不订”判断下列每对事件是不是互斥事件；如果是，再判断它们是不是对立事件(1)A与C；(2)B与E；(3)B与C；(4)C与E.解(1)由于事件C“至多订一种报纸”中有可能“

18、只订甲报纸”，即事件A与事件C有可能同时发生，故A与C不是互斥事件(2)事件B“至少订一种报纸”与事件E“一种报纸也不订”是不可能同时发生的，故B与E是互斥事件由于事件B不发生可导致事件E一定发生，且事件E不发生会导致事件B一定发生，故B与E还是对立事件(3)事件B“至少订一种报纸”中有这些可能：“只订甲报纸”、“只订乙报纸”、“订甲、乙两种报纸”，事件C“至多订一种报纸”中有这些可能：“一种报纸也不订”、“只订甲报纸”、“只订乙报纸”，由于这两个事件可能同时发生，故B与C不是互斥事件(4)由(3)的分析，事件E“一种报纸也不订”是事件C的一种可能，即事件C与事件E有可能同时发生，故C与E不是

19、互斥事件变式训练：判断下列各对事件是不是互斥事件或对立事件：某小组有3名男生和2名女生，从中任选2名同学去参加演讲比赛，其中(1)恰有1名男生和恰有2名男生；(2)至少有1名男生和至少有1名女生；(3)至少有1名男生和全是女生解(1)是互斥事件，不是对立事件“恰有1名男生”实质选出的是“1名男生和1名女生”，与“恰有2名男生”不可能同时发生，所以是互斥事件，不是对立事件(2)不是互斥事件，也不是对立事件“至少有1名男生”包括“1名男生和1名女生”与“2名都是男生”两种结果，“至少有1名女生”包括“1名女生和1名男生”与“2名都是女生”两种结果，它们可能同时发生(3)是互斥事件且是对立事件“至少

20、有1名男生”，即“选出的2人不全是女生”，它与“全是女生”不可能同时发生，且其并事件是必然事件，所以两个事件互斥且对立 考点二 随机事件的频率与概率例2(2015·北京)某超市随机选取1 000位顾客，记录了他们购买甲、乙、丙、丁四种商品的情况，整理成如下统计表，其中“”表示购买，“×”表示未购买. 商品顾客人数甲乙丙丁100×217××200×300××85×××98×××(1)估计顾客同时购买乙和丙的概率；(2)估计顾客在甲、乙、丙、丁中同时购买3种商

21、品的概率；(3)如果顾客购买了甲，则该顾客同时购买乙、丙、丁中哪种商品的可能性最大？解(1)从统计表可以看出，在这1 000位顾客中有200位顾客同时购买了乙和丙，所以顾客同时购买乙和丙的概率可以估计为0.2.(2)从统计表可以看出，在这1 000位顾客中，有100位顾客同时购买了甲、丙、丁，另有200位顾客同时购买了甲、乙、丙，其他顾客最多购买了2种商品所以顾客在甲、乙、丙、丁中同时购买3种商品的概率可以估计为0.3.(3)与(1)同理，可得：顾客同时购买甲和乙的概率可以估计为0.2，顾客同时购买甲和丙的概率可以估计为0.6，顾客同时购买甲和丁的概率可以估计为0.1.所以，如果顾客购买了甲，

22、则该顾客同时购买丙的可能性最大变式训练：某企业生产的乒乓球被奥运会指定为乒乓球比赛专用球，目前有关部门对某批产品进行了抽样检测，检查结果如下表所示：抽取球数n501002005001 0002 000优等品数m45921944709541 902优等品频率(1)计算表中乒乓球优等品的频率；(2)从这批乒乓球产品中任取一个，质量检查为优等品的概率是多少？(结果保留到小数点后三位)解(1)依据公式f，计算出表中乒乓球优等品的频率依次是0.900,0.920,0.970,0.940,0.954,0.951.(2)由(1)知，抽取的球数n不同，计算得到的频率值不同，但随着抽取球数的增多，频率在常数0.

23、950的附近摆动，所以质量检查为优等品的概率约为0.950.考点三：互斥事件、对立事件的概率命题点1互斥事件的概率例3袋中有12个小球，分别为红球、黑球、黄球、绿球，从中任取一球，得到红球的概率是，得到黑球或黄球的概率是，得到黄球或绿球的概率也是，试求得到黑球、黄球和绿球的概率各是多少？解方法一从袋中选取一个球，记事件“摸到红球”“摸到黑球”“摸到黄球”“摸到绿球”分别为A，B，C，D，则有P(A)，P(BC)P(B)P(C)，P(CD)P(C)P(D)，P(BCD)P(B)P(C)P(D)1P(A)1，解得P(B)，P(C)，P(D)，因此得到黑球、黄球、绿球的概率分别是，.方法二设红球有n

24、个，则，所以n4，即红球有4个又得到黑球或黄球的概率是，所以黑球和黄球共5个又总球数是12，所以绿球有12453(个)又得到黄球或绿球的概率也是，所以黄球和绿球共5个，而绿球有3个，所以黄球有532(个)所以黑球有124323(个)因此得到黑球、黄球、绿球的概率分别是，.命题点2对立事件的概率例4某商场有奖销售中，购满100元商品得1张奖券，多购多得.1 000张奖券为一个开奖单位，设特等奖1个，一等奖10个，二等奖50个设1张奖券中特等奖、一等奖、二等奖的事件分别为A、B、C，求：(1)P(A)，P(B)，P(C)；(2)1张奖券的中奖概率；(3)1张奖券不中特等奖且不中一等奖的概率解(1)

25、P(A)，P(B)，P(C).故事件A，B，C的概率分别为，.(2)1张奖券中奖包含中特等奖、一等奖、二等奖设“1张奖券中奖”这个事件为M，则MABC.A、B、C两两互斥，P(M)P(ABC)P(A)P(B)P(C).故1张奖券的中奖概率为.(3)设“1张奖券不中特等奖且不中一等奖”为事件N，则事件N与“1张奖券中特等奖或中一等奖”为对立事件，P(N)1P(AB)1.故1张奖券不中特等奖且不中一等奖的概率为.变式训练：国家射击队的队员为在射击世锦赛上取得优异成绩，正在加紧备战，经过近期训练，某队员射击一次命中710环的概率如下表所示：命中环数10环9环8环7环概率0.320.280.180.1

26、2求该射击队员射击一次：(1)射中9环或10环的概率；(2)命中不足8环的概率解记事件“射击一次，命中k环”为Ak(kN，k10)，则事件Ak彼此互斥(1)记“射击一次，射中9环或10环”为事件A，那么当A9，A10之一发生时，事件A发生，由互斥事件的加法公式得P(A)P(A9)P(A10)0.280.320.60.(2)设“射击一次，至少命中8环”的事件为B，则表示事件“射击一次，命中不足8环”又BA8A9A10，由互斥事件概率的加法公式得P(B)P(A8)P(A9)P(A10)0.180.280.320.78.故P()1P(B)10.780.22.因此，射击一次，命中不足8环的概率为0.2

27、2.当堂达标：1一个人打靶时连续射击两次，事件“至少有一次中靶”的互斥事件是()A至多有一次中靶 B两次都中靶C只有一次中靶 D两次都不中靶答案D解析射击两次的结果有：一次中靶；两次中靶；两次都不中靶，故至少一次中靶的互斥事件是两次都不中靶2从某班学生中任意找出一人，如果该同学的身高小于160 cm的概率为0.2，该同学的身高在160,175(单位：cm)内的概率为0.5，那么该同学的身高超过175 cm的概率为()A0.2 B0.3 C0.7 D0.8答案B解析因为必然事件发生的概率是1，所以该同学的身高超过175 cm的概率为10.20.50.3，故选B.3(2015·湖北)我国

28、古代数学名著数书九章有“米谷粒分”题：粮仓开仓收粮，有人送来米1 534石，验得米内夹谷，抽样取米一把，数得254粒内夹谷28粒，则这批米内夹谷约为()A134石 B169石C338石 D1 365石答案B解析因为样品中米内夹谷的比为，所以这批米内夹谷为1 534×169(石)4给出下列三个命题，其中正确的命题有_个有一大批产品，已知次品率为10%，从中任取100件，必有10件是次品；做7次抛硬币的试验，结果3次出现正面，因此正面出现的概率是；随机事件发生的频率就是这个随机事件发生的概率答案0解析错，不一定是10件次品；错，是频率而非概率；错，频率不等于概率，这是两个不同的概念5(教

29、材改编)袋中装有9个白球，2个红球，从中任取3个球，则恰有1个红球和全是白球；至少有1个红球和全是白球；至少有1个红球和至少有2个白球；至少有1个白球和至少有1个红球在上述事件中，是对立事件的为_答案解析是互斥不对立的事件，是对立事件，不是互斥事件巩固提高案 日积月累 提高自我1下列命题：将一枚硬币抛两次，设事件M：“两次出现正面”，事件N：“只有一次出现反面”，则事件M与N互为对立事件；若事件A与B互为对立事件，则事件A与B为互斥事件；若事件A与B为互斥事件，则事件A与B互为对立事件；若事件A与B互为对立事件，则事件AB为必然事件，其中，真命题是()A BC D答案B解析对，一枚硬币抛两次，

30、共出现正，正，正，反，反，正，反，反四种结果，则事件M与N是互斥事件，但不是对立事件，故错；对，对立事件首先是互斥事件，故正确；对，互斥事件不一定是对立事件，如中两个事件，故错；对，事件A、B为对立事件，则一次试验中A、B一定有一个要发生，故正确故B正确2围棋盒子中有多粒黑子和白子，已知从中取出2粒都是黑子的概率为，都是白子的概率是，则从中任意取出2粒恰好是同一色的概率是()A. B. C. D1答案C解析设“从中取出2粒都是黑子”为事件A，“从中取出2粒都是白子”为事件B，“任意取出2粒恰好是同一色”为事件C，则CAB，且事件A与B互斥所以P(C)P(A)P(B).即任意取出2粒恰好是同一色

31、的概率为.3在5张电话卡中，有3张移动卡和2张联通卡，从中任取2张，若事件“2张全是移动卡”的概率是，那么概率是的事件是()A至多有一张移动卡 B恰有一张移动卡C都不是移动卡 D至少有一张移动卡答案A解析至多有一张移动卡包含“一张移动卡，一张联通卡”“两张全是联通卡”两个事件，它是“2张全是移动卡”的对立事件，故选A.4从存放的号码分别为1,2,3，10的卡片的盒子中，有放回地取100次，每次取一张卡片并记下号码，统计结果如下：卡片号码12345678910取到次数138576131810119则取到号码为奇数的卡片的频率是()A0.53 B0.5 C0.47 D0.37答案A解析取到号码为奇

32、数的卡片的次数为：1356181153，则所求的频率为0.53.故选A.5对一批产品的长度(单位：毫米)进行抽样检测，下图为检测结果的频率分布直方图根据标准，产品长度在区间20,25)上的为一等品，在区间15,20)和25,30)上的为二等品，在区间10,15)和30,35)上的为三等品用频率估计概率，现从该批产品中随机抽取一件，则其为二等品的概率为()A0.09 B0.20 C0.25 D0.45答案D解析设区间25,30)对应矩形的另一边长为x，则所有矩形面积之和为1，即(0.020.040.060.03x)×51，解得x0.05.产品为二等品的概率为0.04×50.0

33、5×50.45.6在200件产品中，有192件一级品，8件二级品，则下列事件：在这200件产品中任意选出9件，全部是一级品；在这200件产品中任意选出9件，全部是二级品；在这200件产品中任意选出9件，不全是二级品其中_是必然事件；_是不可能事件；_是随机事件答案7已知某运动员每次投篮命中的概率都为40%，现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率：先由计算器产生0到9之间取整数值的随机数，指定1,2,3,4表示命中，5,6,7,8,9,0表示不命中；再以每三个随机数为一组，代表三次投篮的结果经随机模拟产生了如下20组随机数：907966191925271932812

34、458569683431257393027556488730113537989据此估计，该运动员三次投篮恰有两次命中的概率为_答案0.25解析20组随机数中表示三次投篮恰好有两次命中的是191,271,932,812,393，其频率为0.25，以此估计该运动员三次投篮恰有两次命中的概率为0.25.8若随机事件A，B互斥，A，B发生的概率均不等于0，且P(A)2a，P(B)4a5，则实数a的取值范围是_答案(，解析由题意可知，<a.9(2014·陕西)某保险公司利用简单随机抽样方法，对投保车辆进行抽样，样本车辆中每辆车的赔付结果统计如下：赔付金额(元)01 0002 0003 0004 000车辆数(辆)500130100150120(1)若每辆车的投保金额均为2 800元，估计赔付金额大于投保金额的概率；(2)在样本车辆中，车主是新司机的占10%，在赔付金额为4 000元的样本车辆中，车主是新司机的占20%，估计在已投保车辆中，新司机获赔金额为4 000元的概率解(1)设A表示事件“赔付金额为3 000元”，B表示事件“赔付金额为4 000元”，以频率估计概率得P(A)0.15，P(B)0.12.由于投保金额为2 800元，赔付金额大于投保金额对应的情形是赔付金额为3 000元和4 000元，所以其概率为P(A)P(B)0.150.120.27