2021学年九年级数学下册第二十七章相似27.2相似三角形27.2.1相似三角形的判定第2课时相似三角形判定定理12课件（新版）新人教版

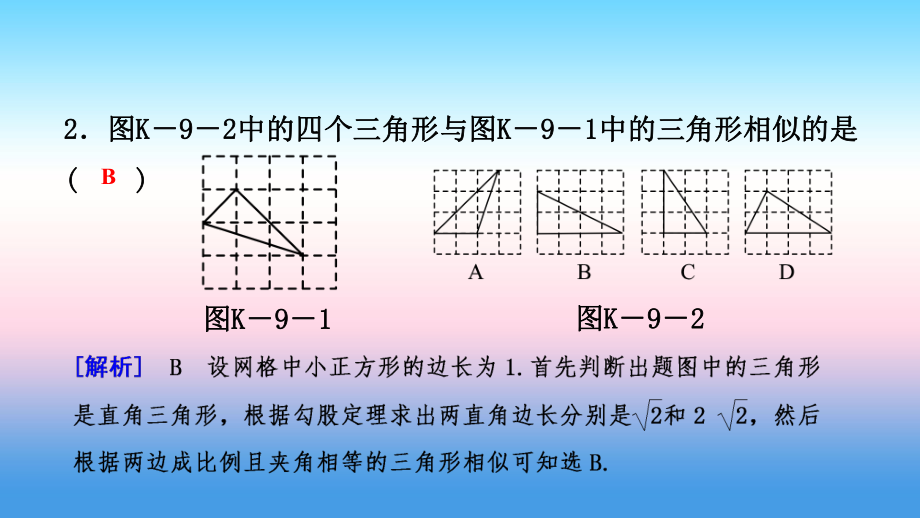
1、第二十七章相似第二十七章 相似第2课时相似三角形判定定理1,2一、一、 选择题选择题 A2 2图图K K9 92 2中的四个三角形与图中的四个三角形与图K K9 91 1中的三角形相似的是中的三角形相似的是( () )图图K K9 91 1图图K K9 92 2B3 3如图如图K K9 93 3，四边形，四边形ABCDABCD的对角线的对角线ACAC，BDBD相交于点相交于点O O，且，且将这个四边形分成将这个四边形分成四个三角形若四个三角形若OAOAOCOC OBOBODOD，则下列结论中一定正确的是则下列结论中一定正确的是( () )A A和和相似相似 B B和和相似相似C C和和相似相似

2、 D D和和相似相似图图K K9 93 3 解析解析 B B 两个三角形两边的比相等，并且相两个三角形两边的比相等，并且相应的夹角相等，那么这两个三角形相似应的夹角相等，那么这两个三角形相似B4 4已知线段已知线段ADAD，BCBC相交于点相交于点O O，OBOBODOD3131，若，若OAOA12 12 cmcm，OCOC4 cm4 cm，ABAB30 cm30 cm，则，则CDCD的长为的长为( () )A A5 cm B5 cm B10 cm C10 cm C45 cm D45 cm D90 cm90 cmB5 5如图如图K K9 94 4，在方格纸中，在方格纸中，ABCABC和和EPD

3、EPD的顶点均在格的顶点均在格点上，要使点上，要使ABCABCEPDEPD，则点，则点P P所在的格点为所在的格点为( () )A AP P1 1 B BP P2 2C CP P3 3 D DP P4 4图图K K9 94 4CB二、填空题二、填空题 297 7如图如图 K K9 95 5，D D是是ABCABC内的一点内的一点，连接连接BDBD并延长到点并延长到点E E，连接连接ADAD，AEAE，若若ADADABABDEDEBCBCAEAEACAC，且且CAECAE2929，则则BADBAD_. 图图K K9 95 58 8如图如图K K9 96 6所示，所示，D D是是ABCABC平分线

4、上的一点，平分线上的一点，ABAB15 cm15 cm，BDBD12 cm12 cm，要使，要使ABDABDDBCDBC，则，则BCBC的长为的长为_cm._cm.图图K K9 96 6 485 9 9如图如图K K9 97 7所示，正方形所示，正方形ABCDABCD的边长为的边长为2 2，AEAEEBEB，MNMN1 1，线段线段MNMN的两端分别在的两端分别在CBCB，CDCD上滑动，当上滑动，当CMCM_时，时，AEDAED与以与以M M，N N，C C为顶点的三角形相似为顶点的三角形相似图图K K9 97 75 55 5或或2 2 5 55 5 10如图如图 K98，已知已知ABC，D

5、CE，FEG，HGI 是是 4个全等的等腰三角形个全等的等腰三角形，底边底边 BC，CE，EG，GI 在同一直线上在同一直线上，且且 AB2，BC1，连接连接 AI，交交 FG 于点于点 Q，则则 QI_.链接听课例链接听课例2归纳总结归纳总结 图图K K9 98 843 三、解答题三、解答题 图图K K9 99 91111 如图如图K K9 99 9， 已知已知ABABDBDBBCBCBEBECACAEDED， 则则ABDABD 与与CBECBE 相等吗？相等吗？为什么？为什么？ 1212如图如图K K9 91010，在，在ABCABC中，已知中，已知ABABACAC，点，点D D，E E，

6、B B，C C在同一条直线上，且在同一条直线上，且ABAB2 2BDCE.BDCE.求证：求证：ABDABDECA.ECA.图图K K9 91010证明：证明：ABABACAC，ABCABCACBACB， ABDABDACE.ACE. ABAB2 2BDCEBDCE， ABABCECEBDBDABAB，即，即ABABECECBDBDCACA， ABDABDECA.ECA. 1313如图如图K K9 91111 所示所示，在正方形在正方形 ABCDABCD 中中，已知已知 P P 是是 BCBC 边上的边上的点点，且且 BPBP3PC3PC，Q Q 是是 CDCD 的中点的中点，ADQADQ 与

7、与QCPQCP 相似吗？请说明相似吗？请说明理由理由 链接听课例链接听课例2 2归纳总结归纳总结 图图K K9 91111 解析解析 ADQADQ与与QCPQCP中已有一角对应相等，条件中已有一角对应相等，条件中告诉了边之间的关系，判断两三角形是否相似，中告诉了边之间的关系，判断两三角形是否相似，就是看夹已知角的两边是否对应成比例就是看夹已知角的两边是否对应成比例解：解：相似理由如下：相似理由如下： 设设 PCPCa a，则，则 BPBP3a3a，BCBCBPBPPCPC4a.4a. Q Q 是是 CDCD 的中点，的中点，DQDQQCQC1 12 2CDCD2a2a， ADADQCQC4a4

8、a2a2a2 2，DQDQCPCP2a2aa a2 2，ADADQCQCDQDQCPCP. . 又又D DC C9090，ADQADQQCP.QCP. 点评点评 当两个三角形中已有一个角对应相等时，要判定两三当两个三角形中已有一个角对应相等时，要判定两三角形相似，只需证明夹这个角的两边对应成比例即可角形相似，只需证明夹这个角的两边对应成比例即可1414 如图如图K K9 91212， 在在ABCABC 中中， 点点 D D， E E 分别在边分别在边 ABAB， ACAC 上上， AEDAEDB B，射线射线 AGAG 分别交线段分别交线段 DEDE，BCBC 于点于点 F F，G G，且且A

9、DADACACDFDFCGCG. . ( (1 1) )求证：求证：ADFADFACGACG； ( (2 2) )若若ADADACAC1 12 2，求求AFAFFGFG的值的值 图图K K9 91212解：解：(1)(1)证明：因为证明：因为AEDAEDB B，DAEDAECABCAB， 所以所以ADFADFC.C. 又因为又因为 ADADACACDFDFCGCG，所以，所以ADFADFACG.ACG. (2)(2)因为因为ADFADFACGACG，所以，所以ADADACACAFAFAGAG. . 又因为又因为 ADADACAC1 12 2，所以，所以AFAFAGAG 1 12 2，所以，所以

10、AFAFFGFG 1.1. 图图K K9 91313动态探究动态探究 如图如图K K9 91313，在，在RtRtABCABC中，中，AA9090，BCBC10 10 cmcm，ACAC6 6 cmcm，在线段，在线段BCBC上，动点上，动点P P以以2 2 cmcm/ /s s的速度从点的速度从点B B向点向点C C匀速运匀速运动；同时在线段动；同时在线段CACA上，点上，点Q Q以以a a cmcm/ /s s的速度从点的速度从点C C向点向点A A匀速运动，匀速运动，当点当点P P到达点到达点C(C(或点或点Q Q到达点到达点A)A)时，时，两点停止运动两点停止运动( (1 1) )当点

11、当点 P P 运动运动30301111 s s时时， CPQCPQ 与与ABCABC 第一次相似第一次相似， 求点求点 Q Q 的速度；的速度； ( (2 2) )在在( (1 1) )的条件下的条件下，当当CPQCPQ 与与ABCABC 第二次相似时第二次相似时，求点求点 P P 总共总共运动了多少秒运动了多少秒 图图K K9 91313解：解：(1)(1)如图如图，BPBP303011112 260601111( (cmcm) ) 依题意，知当依题意，知当QCQCACACPCPCBCBC时，时，CPQCPQ 与与ABCABC 第一次相似，第一次相似， 即即30a30a11116 61010606011111010，解得，解得 a a1 1，点点 Q Q 的速度为的速度为 1 1 cmcm/ /s s