运筹学－图与网络分析

1、第十三章图与网络分析图论的第篇论文：1736年，瑞士数学家欧拉的“依据几何位置的解题方法”有效解决了哥尼斯堡七桥难题。图论的第一本专著：1936年，匈牙利数学家狄.考尼格的 "有限图与无限图的理论”。哥尼斯堡七桥问题:图 13.1.1(a)d哥尼斯堡城中有一条普雷格尔河，河中有b、d两岛， 河上有七座桥，如图13.1.1(a)。当时那里的居民热衷于这样 的游戏：一个散步者能否连续走过七座桥，且走过每桥只一 次，最后回到出发点。欧拉将此问题归结为图13.1.1(b)的一笔画问题，证明了 这是不可能的。当且仅当图中全部顶点都与偶数条线相关联 时，该图才能一笔画成。图论中的图用点代表所研究

2、的对象，用连线代表两对象 之间的特定关系。这种图与几何图形、函数图形不同。13.1图与网络的基本知识一、无向图1.无向图边：点与点之间的没有方向性的连线。连接vi、vj两 点的边记作vi，vj或vj, vjo无向图：由点和边构成的图，记作g=(v, e),式中 v是图g的点的集合，e是图g的边集合。v = vp v2，v5e = ep e?,ei= vp v2 = v2, vj2.简单图环：两个端点重合的边。多重边：两个端点之间的边数22。简单图：无环也无多重边的无向图。以后说到图，如 无特殊说明，均指简单图。3.连通图路：图中一个以顶点始、以顶点终的顶点和边的交替 序列（允许有顶点重复和边重

3、复）。图 13.1.2 中,（v3,知 v2，ep vp e8, v5, e9 g v）是一条路。简单路：如果出现在一条路中的边都互不相同（允许 顶点重复，边不重复），则这条路叫简单路。图 13.1.2 中，（v3, e3, v2，ep vp e8, v5, e9, v2） 是一条简单路。初级路：如果出现在一条路中的顶点都互相不同，则 这条路叫初级路。（顶点不重复，边当然也不重复） 一般情况下，我们寻求的都是初级路。图 13.1.2 中，（v3, e3, v2，ep v）是一条初级路。连通图：图g屮，若任何两个不同的顶点之间，至少存在一条路，则称g是连通图。二、有向图1. 有向图弧：点与点之间

4、的有方向性的(用箭头表示)连线。 若一条弧a=(vj, vj),则称vi为a的始点，比为a 的终点，弧a是从匕指向v)的。图 13.1.3有向图：由点和弧构成的图，记作d=(v, a),式中 v是图d的点集合，a是图d的弧集合。v = v1，v2，v5a = a, a?,39al = (vp v2)h(v2，vi)2. 简单有向图环：两个端点重合的弧。多重弧：两个端点之间的同向弧数22。简单有向图：无环也无多重弧的有向图。简单有向图 中，ai = (vi，vj) =(i, j)3路与有向路设有向图为 d=(v,a), p= vp ap v2，a2? vk.p ak.pvd是一个由d的顶点和弧组

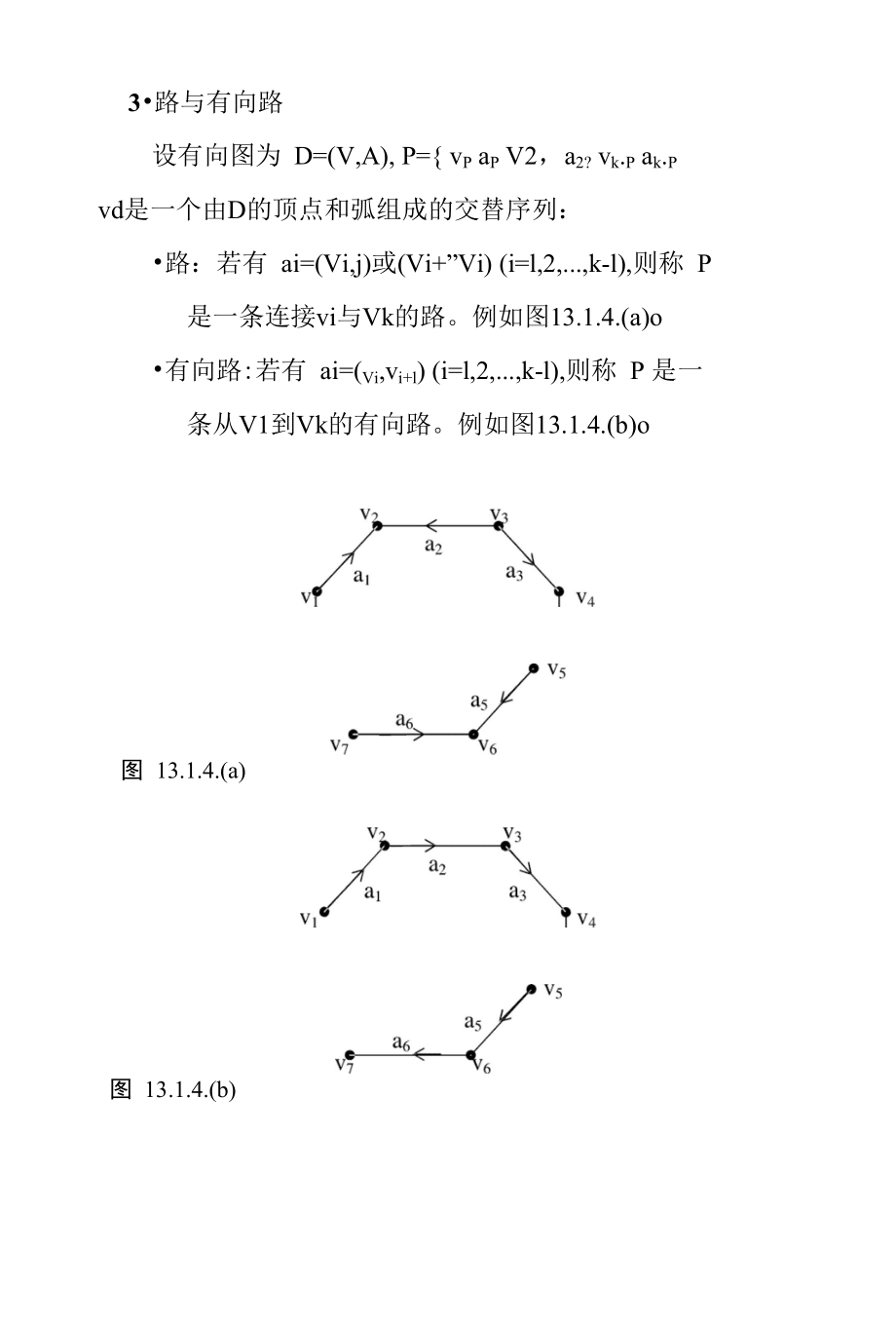
5、成的交替序列：路：若有 ai=(vi,j)或(vi+”vi) (i=l,2,.,k-l),则称 p是一条连接vi与vk的路。例如图13.1.4.(a)o有向路:若有 ai=(vi,vi+l) (i=l,2,.,k-l),则称 p 是一条从v1到vk的有向路。例如图13.1.4.(b)o图 13.1.4.(a)图 13.1.4.(b)4.前向弧与后向弧前向弧：有一条连接顶点v与vk的路，给定这条路 的一个假定方向，例如从v1到vk，则方向与路的假 定方向相同的弧叫“前向弧"。后向弧：上述情况下，方向与路的假定方向相反的弧, 叫"后向弧”。图13.14(a)中，假定路的方向是从

6、vi到v7，则a?、 a6是后向弧，其它均为前向弧。三、网络网络：给定有向图d=(v, a),在v中指定了起点与 终点，其余点称为中间点。对于每一条弧(vi,vj)wa, 对应有一个数qi，称为弧上的“权”，这种赋权有向 图d称为网络。每条弧可有一个或多个''权”，“权” 的含义可以是各种各样的。13.2最短路问题、最短路问题举例v6 (& 4)v5v)(0,1：v3 n 、(2, 1)图 1321图13.2.1是一个简单有向图，每条弧（i, j）都有一个长度cjj,求起点v1到终点v6的最短有向路。最短路问题属于线性规划问题，是运输问题的特例。二、dijkstra算法

7、（双标号法）本算法适用于每条弧的长度cijno的情况双标号：对一般顶点vi都赋予两个标号（厶，k）,厶是从起点v1到vi的最短路长度ki是最短路径上m点前面一个邻点的下标（正整数）。dijkstra算法基本步骤：1. 给起点vi标(0,1)2. 求出此时的点集合i, j与弧集合ai：具有未赋标号邻点的已赋标号点vi的下标i的集合 (已赋标号点t邻点)j： i中各点所具有的未赋标号邻点vj的下标j的集合a； (i,j)liei, jej(弧的指向由 itj)例中第一次迭代：1= 1 j=2, 3, 4 a=(1,2) (1,3) (1,4)3. 若上述弧集合a是空集，则得到一族最优结果。若上述弧

8、集合a不是空集，转步骤4。4. 对a中的每条弧(i, j),分别计算sq = li + cij,令其中 sij值最小的弧为(c, d)例中：s)2 =/ +c 12=0+3=3s13 =/1 +c 13=0+2=2s4 =l +c4=°+5=5min(s12, s13, s14) = s3 =2即 scd=2, c=l, d=35. 给弧(c, d)的终点vd标双标号gd, c),返回步骤2。例中：给v3标(2, 1)以上，经过一个循环的计算，求出v到一个顶点vj的最 短路径及长度，使一个顶点v)得到双标号。图中共有n个顶 点，最多计算(ml)个循环，即可得最后结果。例中第二次迭代：

9、i= 1, 3 j=2, 4 a=(1, 2) (1,4) (3, 4) s34 =】3 +c34=2+1 =3 min = si2= s34 =3 给 v2标(3,1), 给v4标(3,3) 第三次迭代：i=2,4j=6a=(2, 6) (4, 6)s26 =】2 +c26=3+7=10s46 =仃 +c46=3+5=8=min 给v6标(& 4)第四次迭代：i=j=a= 4),停止迭代。最后结果：此吋v5未得到标号，表明从v1 v5无有向路。从v到v6的最短路径是vt v3t v4t v6,最短距离为8o得到一族最优结果。 dijkstra算法是一个公认的好算法(多项式算法)。三、

10、无向图上的dijkstra算法将无向图t有向图：每一条边用方向相反的两条弧代替。直接在无向图上用dijkstra算法求解：与相应有向图上的 求解相比，邻点个数可能增加，集合i、j、a中的元素均 可能增加，所有顶点都会得到标号，最优结果可能更优。四、求解带负权的最短路问题如果权值有负的，则最短路问题可采用动态规划屮不定 期最短路径问题的解法(函数迭代法、策略迭代法)。133最大流问题一、网络上的最大流问题概述1. 网络上的最大流问题举例v2v54vv73»图 13.3.1例：图13.3.1中，弧旁数字为该弧容量列，弧的方向就 是允许流的方向。现在要把一批货物由起点v1运到终点v7 去，

11、每条弧上通过的货物总量不能超过这条弧的容量。应怎 样安排运输,才能使从起点v.到终点v7的总运量达到最大？2. 什么叫可行流？设切是通过弧(i, j)的运输量，则满足下面二条件的组 网络流国叫可行流：(1) 可行条件：对每一条弧(i,j),有owfijwqj(2) 守恒条件:对顶点旳而言式中a是所有以百为起点的弧的集合，b是所有以w为终点的弧的集合。上述f20,称为这个可行流的值(运输总量)。3. 最大流问题是线性规划问题例：设各弧(i,j)上的可行流为角，总的可行流的值为f： 目标函数：max f约束条件：f2 +f4 +fi3 =f坛+彳24才12 =0十57 _彳67 = _fowfij

12、wcij(i=l, 2,，6； j=2, 3,，7)二、ford-fulkerson 方法(1956 年)1. 什么叫可扩充路？设fij是一组可行流，若存在一条连接v1与vn的路p(假 设其方向为由v1到vn),满足(1) 在p的所有前向弧上ffcij(2) 在p的所有后向弧上血0则称p是关于流垢的一条可扩充路。2. 引理1对于一个可行流琮1)来说，如果能找到一条可扩充路p,那么血就可以改进成一个值更大的可行流 fij(2) o3. 定理1已知肉是网络的一个可行流，且对于切而言，不存在 可扩充路，贝ll切是最大流。4. 算法步骤(1) 给泄一组初始可行流血及其值f例如，可给定初始值为全0。(2

13、) 寻找一条可扩充路p若不存在可扩充路，已得最大流；若存在可扩充路p,转步骤(3)。(3) 在p上将偽增流为偽。返回步骤。令e ! = mincij -血i (i,j)是p的前向弧若p上没有前向弧，令e i =令e 2=min血i (i, j)是p的后向弧若p上没有后向弧，令e 2= +°°增流量 £ = min( e b e 2)r f0)(若(i,j)不在p±)丄ij故fj2)= j + £ (若(i,j)是p的前向弧)f补)£ (若(i, j)是p的后向弧)增流的结果或至少有一条前向弧上的流量血上升到列，成了“饱和弧”。或至少有

14、一条后向弧上的流量血下降到0,成了 “零流弧”。(相当丁逆着弧的方向上有值为fij的增流量)临界弧饱和弧与零流弧都叫做“临界弧”。5寻找可扩充路p的双标号法寻找可扩充路p时，是从v开始逐步向vn寻找。给每个顶点v）赋两个标号：第一个是k,它表明p上旳前面一个顶点是vk；第二个是"+ ”或”表示vk与舟之间沿箭 头方向的可行流还可增加则表示还可减少图 13.3.2取一点廉进行检查i:vi是一个已标号而未检查的点。对于vi的检查，即是对的所有未标号的邻点vj进行标号(“临界弧”除外)。(1)检查所有以vi为起点的弧(i,j),若fijvcij,且vj未标 号，则给vj标(i, +) o

15、检查所有以w为终点的弧(j, i),若切0,且勺未标 号，则给vj标(i, -)o 若前向弧(i,j)上有 妒驹,或后向弧(j,i)上有 加0,则 弧是临界的，此时对vj不赋标记。 若vi没有未标号的邻点,则vi已检查完。(5)在出的第二个标号上加一个小圈，呈或g),表示该点已检查完。5. ford-fulkerson 方法的缺点当网络的容量可以取无理数时，用该法可能找不到最 大流。当容量全是正整数时，有时需迭代许多次才能得到最 大流，且迭代次数不仅依赖于网络屮的顶点数n和弧 数m,还依赖丁容量和最大流的值。上述缺点与选取可扩充路时的任意性有关。三、edmonds-karp 方法(1972 年

16、)1. edmonds-karp方法的特点在ford-fulkerson方法的基础上，对标有*的部分遵循 “先标号的顶点先检查”，就可保证每一次迭代找到的可扩 充路是“最短”的(即包含的弧数是最少的)，就能克服 ford-fulkerson方法的缺点。2.计算举例图1检查完毕，给v4标(1)例：用edmonds-karp方法求图13.3.1所示网络的最大流。 解：第一次迭代(见图1),给定初始可行流为全零流，即 f()=0给起点vi标(1, +)检查v：给v2标(1, +),v4 标(1，+), v3 标(1，+),检查完毕，给v1标(1,0)检查v2：给v5标(2, +),检查完毕，给v2标

17、(1,)检查v4：给v6标(4, +),检查巾：没有未标记的邻点，检查完毕，给v3标(1,) 检查v5：给v7标(5, +),检查完毕，给v5标(2,0 ) 至此，终点v7已标号，得p：viv2v5v7f)=min4, 1,7=1, s 2(1)=<, £ (1)=min £ 1 ，£ 2(1)=1f=1第二次迭代，抹去原来的标号，见图2。给起点vi标(1, +)检查v：给v2标(1,+),v4 标(1，+), v3 标(1，+),检查完毕，给v标(1g)检查v2： v5不标，检查完毕，给v2标(1,)% (4, +)(1/+) 4,0图2v2 1j,0 4,3,0v4，+)3,5,a2,0、v7(5,+)8,0检查v*给v5标(4, +),检查v3：没有未标记的邻点,检查完毕，给v3标(1®)给v6标(4, +),检查完毕，给v4标(1g)检查v5：给v7标(5, +),检查完毕，给v5标(4，q )至此，终点v7已标号,得p:v1v4v5v7£=3f(2) =4第七次迭代，得p:v-> v3v