



版权说明:本文档由用户提供并上传,收益归属内容提供方,若内容存在侵权,请进行举报或认领
文档简介
1、空间立体几何图形的截面江苏省前黄高级中学 许云峰教学背景本课为以立体几何的截面图为核心,让学生借助几何画板的实际模拟和探索功能进行学习,由学生自我探究,进行知识迁移,通过类比,自己去尝试并最终解决问题。教师在此过程中进行必要的总结和在学生出现困难时进行指导,由此培养学生思维的独立和发散性,使学生真正成为学习的主体。教学目标:1认知目标:整合几何体的截面情况,形成完整的认知体系。2能力目标:学生利用几何画板探索问题的能力,以培养学生知识迁移能力,发散思维和类比思维能力。3情感目标:培养学生探索创新能力,激发学生学习的热情和积极性。重点与难点重点:空间几何体的截面图的作法;空间旋转体的截面作法。难
2、点:空间几何图形的交点的作法;由极限思想作出空间旋转体的截面图的作法。教学策略与教法设计策略:教师提出问题,然后逐层展开,分步进行研究(需学生进行探索和分析),然后学生进行分组讨论和实际操作,通过自主学习、探究学习、合作学习达到认知的意义建构。教法1演示法:把制作的课件展示给学生,便于学生对知识的深层次的把握,并从中获得启发,从而解决问题。这同时也给学生制作作品提供了模板,让学生明白作品需达到的要求。2谈话法:在教师指导下,由全班或小组成员围绕某一中心问题发表自己的看法,从而进行相互学习、合作学习,集思广益。3成果展示法:将学生制作的作品有选择的展示(以小组为单位进行制作,每个小组推荐12个进
3、行演示),让学生获得成功的喜悦和认同,从而激发学生后续学习的热情。4讨论法:就学生探索所得成果,各小组可自由提问,或者师生共同评价,最后总结成整体观点。教学过程设计先期准备在几何画板中建立立体几何的图形工具包,方便学生在最快的时间内作出准确的立体几何图形,以方便学生进行探究性学习,避免在作图上花费过多时间和精力;同时可以给学生以示范,让学生学会如何作出形象的立体几何直观图。教学目标提出探究空间几何图形上过任意三点的截面1分三个小组对多面体进行协作探究:第一小组:柱体;第二小组:锥体;第三小组:台体。主要探究任意三点的位置和截面的形状。2探究圆锥的截面。分组探究,层层推进,把问题推向纵深通过发挥
4、学生自主学习的特点,并根据几何体的特征可以分类,故我们采取分组进行自我探索,相互协作,小组讨论,师生共同总结等方法进行教学。在此过程中,老师作为主导者,主要为学生提供必要的帮助和方向指引,而学习的过程主要靠学生自我完成。学生进行分组协助学习。每小组的探索活动都可分为三个层次进行:以最简单的图形出发,即三棱柱、三棱锥、三棱台研究任意三点的位置的取法。随后作出过三点的截面(作法依据:公理及其推论),并拖动三点,观察截面的变化情况,从而得出结论,并进行组内交流,形成小组统一观点。对几何体作广度延伸:把底面边数增加,类比的作出截面,并归纳出截面变化情况。最后统一制作成作品,准备交流。在小组探索中,充分
5、发挥学生的自主性,使学生真正成为学习的主人。各小组进行作品展示。各小组可以对展示作品进行讨论,可以对作品提问,讨论(可以应用网络的讨论板块进行或直接的讨论),师生共同评价(或者先学生讨论,教师再总结)。学生在老师的帮助下,加深对知识的理解,从而得到启发,进行知识建构。发散与推广运用极限的逼近思想,来解决圆锥曲线的截面问题,使截面问题达到高潮:既加深对原有问题(多面体的截面)的认识,又引发出问题新的生长点,大大激发学生的探索兴趣。把问题向纵深推广:伴随正棱柱、正棱锥、正棱台底面边数的增加,多面体逼近旋转体,我们能够通过逼近的思想把旋转体的截面作出来呢?旋转体,是母线饶轴旋转而来,故截面与旋转体侧
6、面的交线即为母线与截面交点饶轴旋转而来,由此我们可以作出过母线上任意三点的旋转体的截面了。以圆锥为例,作出圆锥截面,并探究截面的情形。并把圆柱和圆台的问题留在课后,使学生继续进行探究活动。本课教学的主题是学生,这使学生在如何加工信息、怎样推理验证等方面得到锻炼,利于培养学生探索能力,使学生既学到了知识,学到了科学的思想方法,又提高了能力;让学生从整个知识体系中去掌握知识点的来龙去脉,也就是把它的逻辑锁链搞清楚,并尝试从知识体系中寻找新的知识生长点!对同学们的表现进行评价,要及时表扬一些表现好的同学,同时鼓励其他同学,以提高同学们学习的积极性并知道他们进行新的探索,使学生产生后继学习的激情。空间
7、立体几何图形的截面江苏省前黄高级中学 许云峰教学背景本课为以立体几何的截面图为核心,让学生借助几何画板的实际模拟和探索功能进行学习,由学生自我探究,进行知识迁移,通过类比,自己去尝试并最终解决问题。教师在此过程中进行必要的总结和在学生出现困难时进行指导,由此培养学生思维的独立和发散性,使学生真正成为学习的主体。教学目标:1认知目标:整合几何体的截面情况,形成完整的认知体系。2能力目标:学生利用几何画板探索问题的能力,以培养学生知识迁移能力,发散思维和类比思维能力。3情感目标:培养学生探索创新能力,激发学生学习的热情和积极性。重点与难点重点:空间几何体的截面图的作法;空间旋转体的截面作法。难点:
8、空间几何图形的交点的作法;由极限思想作出空间旋转体的截面图的作法。教学对象分析教学对象:高二及高二以上年级学生学生特点:(1)在操作方面:高二年级的学生有一定的电脑操作基础,可以自己操作电脑。但学生的操作水平参差不齐,特别是对数学软件几何画板不够熟悉,还不能熟练地操作,所以在上这节课之前要上预备课,主要教学生软件的使用。要做到能独立操作软件且能较熟练地完成一定的学习任务。(2)在知识方面:高二的学生通过对立体集合内容的学习,对空间立体几何有较为全面的认识,但是空间想象能力还有待进一步提高。本节课让学生自己操作软件,通过同学之间的相互协作及通过网络的交流来发现规律,实现知识的整合。教学策略与教法
9、设计策略:教师提出问题,然后逐层展开,分步进行研究(需学生进行探索和分析),然后学生进行分组讨论和实际操作,通过自主学习、探究学习、合作学习达到认知的意义建构。教法1演示法:把制作的课件展示给学生,便于学生对知识的深层次的把握,并从中获得启发,从而解决问题。这同时也给学生制作作品提供了模板,让学生明白作品需达到的要求。2谈话法:在教师指导下,由全班或小组成员围绕某一中心问题发表自己的看法,从而进行相互学习、合作学习,集思广益。3成果展示法:将学生制作的作品有选择的展示(以小组为单位进行制作,每个小组推荐12个进行演示),让学生获得成功的喜悦和认同,从而激发学生后续学习的热情。4讨论法:就学生探
10、索所得成果,各小组可自由提问,或者师生共同评价,最后总结成整体观点。网络环境分析:一人一机的网络教室和网络控制软件TOP2000等教学过程设计先期准备在几何画板中建立立体几何的图形工具包,方便学生在最快的时间内作出准确的立体几何图形,以方便学生进行探究性学习,避免在作图上花费过多时间和精力;同时可以给学生以示范,让学生了解如何作出形象的立体几何直观图。教学目标提出探究空间几何图形上过任意三点的截面1分三个小组对多面体进行协作探究:第一小组:柱体;第二小组:锥体;第三小组:台体。主要探究任意三点的位置和截面的形状。2探究圆锥的截面。分组探究,层层推进,把问题推向纵深第一小组:探究柱体上过棱上任意
11、三点的截面。1由三棱柱开始,研究其过棱棱上任意三点的截面,探究:(1)任意三点的取法,(2)每种取法下,截面有几种形状,最后总结三棱柱截面情况;学生首先给出取点位置:(图1)三点都在侧棱上;三点都在底面上(一面上两个,另一面上一个);棱上一个,底面上两个(一上,一下或两个在同一底面);侧棱上两个,底面上一个。作出三棱柱,分别画出上述情况,并拖动原始点观察截面图的变化情况,最终得出三棱柱截面的情况:当截面与三棱柱的侧棱不相交时,截面为四边形;当截面与三棱柱的侧棱相交时,截面为四边形或三角形。图12类似探究四棱柱,五棱柱(图2)图2四棱柱:截面可为六边形,五边形,四边形,三角形。五棱柱:截面可为七
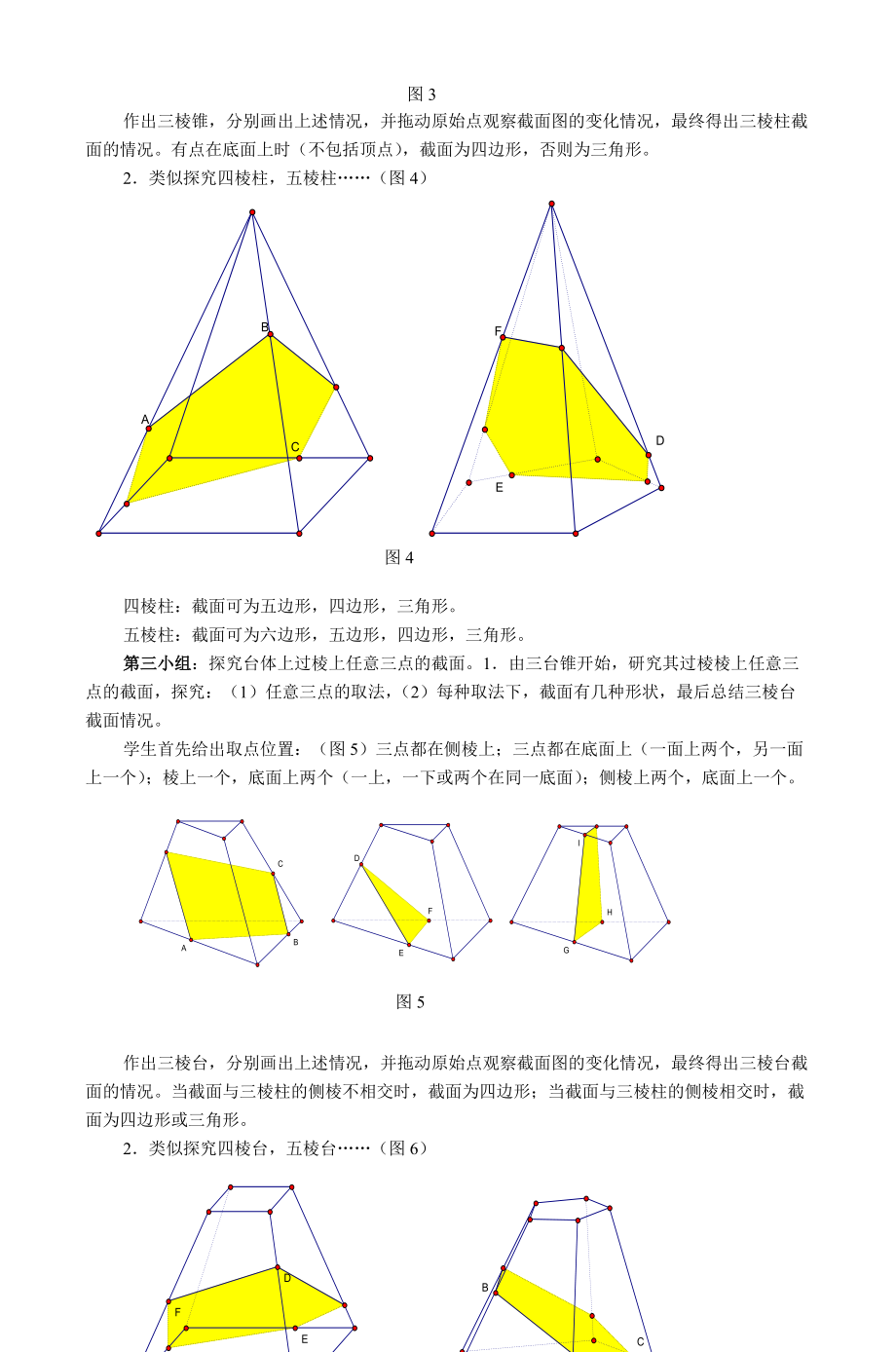
12、边形,六边形,五边形,四边形,三角形。第二小组:探究锥体上过棱上任意三点的截面。1由三棱锥开始,研究其过棱棱上任意三点的截面,探究:(1)任意三点的取法,(2)每种取法下,截面有几种形状,最后总结三棱锥截面情况。学生找出点的取法(图3):两个在侧棱上,一个在底面;两个在底面,一个在侧棱;三个在侧棱。图3作出三棱锥,分别画出上述情况,并拖动原始点观察截面图的变化情况,最终得出三棱柱截面的情况。有点在底面上时(不包括顶点),截面为四边形,否则为三角形。2类似探究四棱柱,五棱柱(图4)图4四棱柱:截面可为五边形,四边形,三角形。五棱柱:截面可为六边形,五边形,四边形,三角形。第三小组:探究台体上过棱
13、上任意三点的截面。1由三台锥开始,研究其过棱棱上任意三点的截面,探究:(1)任意三点的取法,(2)每种取法下,截面有几种形状,最后总结三棱台截面情况。学生首先给出取点位置:(图5)三点都在侧棱上;三点都在底面上(一面上两个,另一面上一个);棱上一个,底面上两个(一上,一下或两个在同一底面);侧棱上两个,底面上一个。图5作出三棱台,分别画出上述情况,并拖动原始点观察截面图的变化情况,最终得出三棱台截面的情况。当截面与三棱柱的侧棱不相交时,截面为四边形;当截面与三棱柱的侧棱相交时,截面为四边形或三角形。2类似探究四棱台,五棱台(图6)图6四棱台:截面可为六边形,五边形,四边形,三角形。五棱台:截面
14、可为七边形,六边形,五边形,四边形,三角形。各小组可以对展示作品进行讨论,可以对作品提问,讨论(可以应用网络的讨论板块进行或直接的讨论),师生共同评价(或者先学生讨论,教师再总结)。学生在老师的帮助下,加深对知识的理解,从而得到启发,进行知识建构。发散与推广把问题向纵深推广:伴随正棱柱、正棱锥、正棱台底面边数的增加,多面体逼近旋转体,我们能够通过逼近的思想把旋转体的截面作出来呢?旋转体,是母线饶轴旋转而来,故截面与旋转体侧面的交线即为母线与截面交点饶轴旋转而来,由此我们可以作出过母线上任意三点的旋转体的截面了。我们以圆锥为例,作出圆锥截面,并探究截面的情形。本课教学的主题是学生,这使学生在如何加工信息、怎样推理验证等方面得到锻炼,利于培养学生探索能力,使学生既学到了知识,学到了科学的思想方法,又提高了能力;让学生从整个知识体系中去
温馨提示
- 1. 本站所有资源如无特殊说明,都需要本地电脑安装OFFICE2007和PDF阅读器。图纸软件为CAD,CAXA,PROE,UG,SolidWorks等.压缩文件请下载最新的WinRAR软件解压。
- 2. 本站的文档不包含任何第三方提供的附件图纸等,如果需要附件,请联系上传者。文件的所有权益归上传用户所有。
- 3. 本站RAR压缩包中若带图纸,网页内容里面会有图纸预览,若没有图纸预览就没有图纸。
- 4. 未经权益所有人同意不得将文件中的内容挪作商业或盈利用途。
- 5. 人人文库网仅提供信息存储空间,仅对用户上传内容的表现方式做保护处理,对用户上传分享的文档内容本身不做任何修改或编辑,并不能对任何下载内容负责。
- 6. 下载文件中如有侵权或不适当内容,请与我们联系,我们立即纠正。
- 7. 本站不保证下载资源的准确性、安全性和完整性, 同时也不承担用户因使用这些下载资源对自己和他人造成任何形式的伤害或损失。
最新文档
- 2025合同的履行与违约经济法教学案例
- 2025水电工承包合同 标准版 模板
- 2025高端公寓前期物业管理服务合同
- 出租彩钢瓦板房合同范本
- 产品外包合同样本
- 煤炭进口措施方案范本
- 2025年辽宁省高三语文三模联考试卷附答案解析
- 乔木合同样本
- 个人房贷合同样本规定
- 出国移民合同标准文本
- 浙江省绍兴市2023年中考英语真题(附答案)
- 龙虎斗(2017广东广州中考记叙文阅读试题含答案)
- 地下铁道-中南大学中国大学mooc课后章节答案期末考试题库2023年
- 废品站劳务合同范本
- 安全生产管理规章制度评审记录
- 教科版五年级科学下册全套测试卷
- 建设工程工程量清单及清单计价2013
- 经颅多普勒超声在脑血管疾病中的应用及临床价值研究
- 云南省体育专业高考部分项目评分标准
- 高盛Marquee平台深度研究报告
- CPR1000核电系统简介

评论
0/150
提交评论