贵州省从江县民族中学2025届高三第二次模拟考试数学试卷含解析

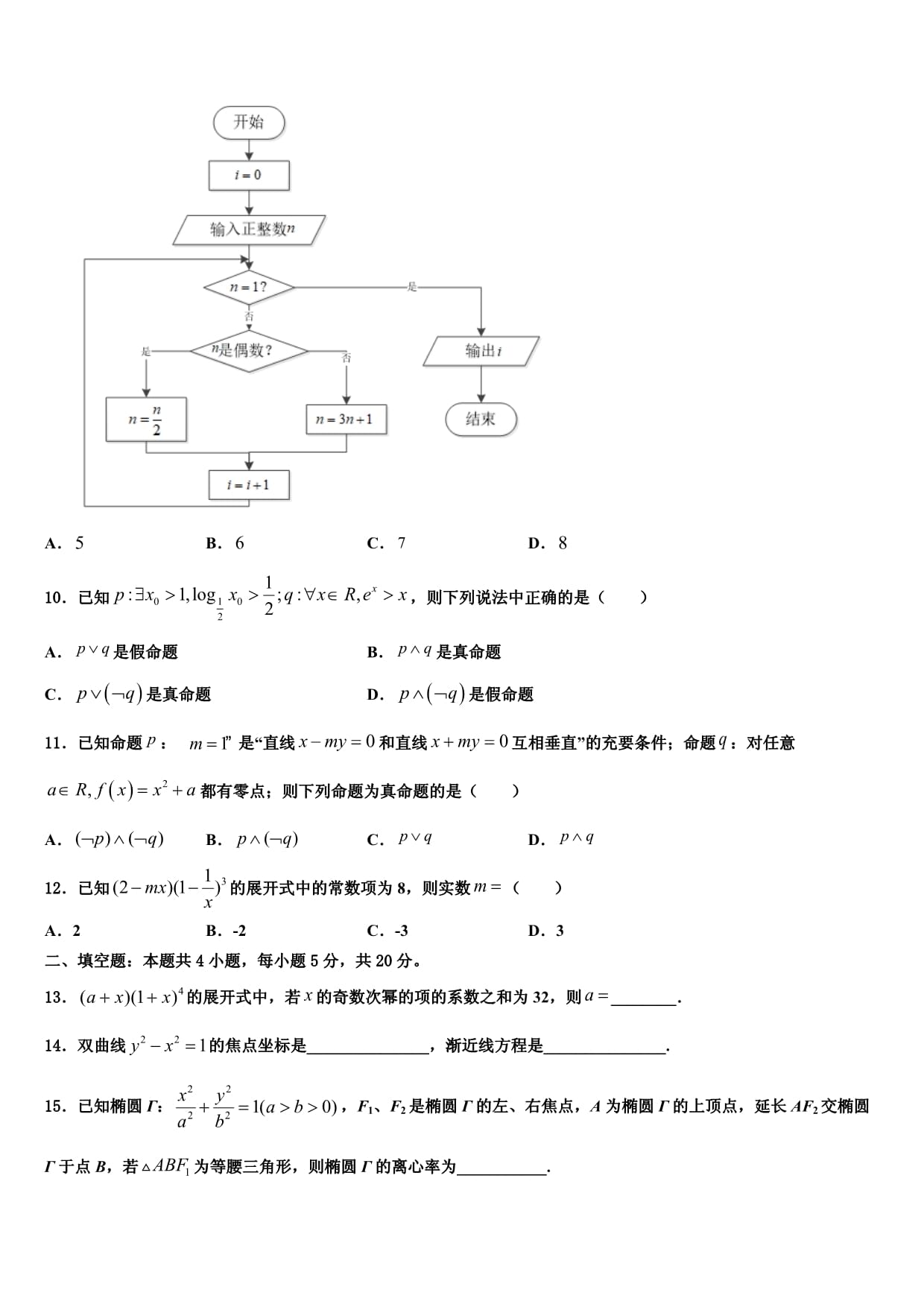
贵州省从江县民族中学2025届高三第二次模拟考试数学试卷注意事项:1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。2．答题时请按要求用笔。3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。5．保持卡面清洁，不要折暴、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。一、选择题：本题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。1．设，命题“存在，使方程有实根”的否定是()A．任意，使方程无实根B．任意，使方程有实根C．存在，使方程无实根D．存在，使方程有实根2．在直三棱柱中，己知，，，则异面直线与所成的角为（）A． B． C． D．3．下图为一个正四面体的侧面展开图，为的中点，则在原正四面体中，直线与直线所成角的余弦值为（）A． B．C． D．4．已知变量，满足不等式组，则的最小值为（）A． B． C． D．5．已知水平放置的△ABC是按“斜二测画法”得到如图所示的直观图，其中B′O′＝C′O′＝1，A′O′＝，那么原△ABC的面积是()A． B．2C． D．6．已知函数的零点为m，若存在实数n使且，则实数a的取值范围是（）A． B． C． D．7．已知函数，则在上不单调的一个充分不必要条件可以是（）A． B． C．或 D．8．过双曲线的右焦点F作双曲线C的一条弦AB，且，若以AB为直径的圆经过双曲线C的左顶点，则双曲线C的离心率为（）A． B． C．2 D．9．很多关于整数规律的猜想都通俗易懂，吸引了大量的数学家和数学爱好者，有些猜想已经被数学家证明，如“费马大定理”，但大多猜想还未被证明，如“哥德巴赫猜想”、“角谷猜想”.“角谷猜想”的内容是：对于每一个正整数，如果它是奇数，则将它乘以再加1；如果它是偶数，则将它除以；如此循环，最终都能够得到.下图为研究“角谷猜想”的一个程序框图.若输入的值为，则输出i的值为（）A． B． C． D．10．已知，则下列说法中正确的是（）A．是假命题 B．是真命题C．是真命题 D．是假命题11．已知命题：是“直线和直线互相垂直”的充要条件；命题：对任意都有零点；则下列命题为真命题的是（）A． B． C． D．12．已知的展开式中的常数项为8，则实数（）A．2 B．-2 C．-3 D．3二、填空题：本题共4小题，每小题5分，共20分。13．的展开式中，若的奇数次幂的项的系数之和为32，则________．14．双曲线的焦点坐标是_______________，渐近线方程是_______________.15．已知椭圆Г：，F1、F2是椭圆Г的左、右焦点，A为椭圆Г的上顶点，延长AF2交椭圆Г于点B，若为等腰三角形，则椭圆Г的离心率为___________.16．若，则的展开式中含的项的系数为_______.三、解答题：共70分。解答应写出文字说明、证明过程或演算步骤。17．（12分）已知函数，设的最小值为m.（1）求m的值；（2）是否存在实数a，b，使得，？并说明理由.18．（12分）如图，在直三棱柱ABC﹣A1B1C1中，∠ABC＝90°，AB＝AA1，M，N分别是AC，B1C1的中点．求证：（1）MN∥平面ABB1A1；（2）AN⊥A1B．19．（12分）已知数列满足.（1）求数列的通项公式；（2）设数列的前项和为，证明：.20．（12分）已知中，角，，的对边分别为，，，已知向量，且．（1）求角的大小；（2）若的面积为，，求．21．（12分）已知函数，且．（1）若，求的最小值，并求此时的值；（2）若，求证:．22．（10分）已知；.（1）若为真命题，求实数的取值范围；（2）若为真命题且为假命题，求实数的取值范围.

参考答案一、选择题：本题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。1、A【解析】

只需将“存在”改成“任意”，有实根改成无实根即可.【详解】由特称命题的否定是全称命题，知“存在，使方程有实根”的否定是“任意，使方程无实根”.故选：A【点睛】本题考查含有一个量词的命题的否定，此类问题要注意在两个方面作出变化：1.量词，2.结论，是一道基础题.2、C【解析】

由条件可看出，则为异面直线与所成的角，可证得三角形中，，解得从而得出异面直线与所成的角．【详解】连接，，如图：又，则为异面直线与所成的角.因为且三棱柱为直三棱柱，∴∴面，∴，又，，∴，∴，解得.故选C【点睛】考查直三棱柱的定义，线面垂直的性质，考查了异面直线所成角的概念及求法，考查了逻辑推理能力，属于基础题．3、C【解析】

将正四面体的展开图还原为空间几何体，三点重合，记作，取中点，连接，即为与直线所成的角，表示出三角形的三条边长，用余弦定理即可求得.【详解】将展开的正四面体折叠，可得原正四面体如下图所示，其中三点重合，记作：则为中点，取中点，连接，设正四面体的棱长均为，由中位线定理可得且，所以即为与直线所成的角，，由余弦定理可得，所以直线与直线所成角的余弦值为，故选：C.【点睛】本题考查了空间几何体中异面直线的夹角，将展开图折叠成空间几何体，余弦定理解三角形的应用，属于中档题.4、B【解析】

先根据约束条件画出可行域，再利用几何意义求最值.【详解】解：由变量，满足不等式组，画出相应图形如下：可知点,，在处有最小值，最小值为.故选：B.【点睛】本题主要考查简单的线性规划，运用了数形结合的方法，属于基础题.5、A【解析】

先根据已知求出原△ABC的高为AO＝，再求原△ABC的面积.【详解】由题图可知原△ABC的高为AO＝，∴S△ABC＝×BC×OA＝×2×＝，故答案为A【点睛】本题主要考查斜二测画法的定义和三角形面积的计算，意在考察学生对这些知识的掌握水平和分析推理能力.6、D【解析】

易知单调递增,由可得唯一零点,通过已知可求得,则问题转化为使方程在区间上有解,化简可得,借助对号函数即可解得实数a的取值范围.【详解】易知函数单调递增且有惟一的零点为，所以，∴，问题转化为：使方程在区间上有解，即在区间上有解，而根据“对勾函数”可知函数在区间的值域为，∴.故选D．【点睛】本题考查了函数的零点问题,考查了方程有解问题,分离参数法及构造函数法的应用,考查了利用“对勾函数”求参数取值范围问题,难度较难.7、D【解析】

先求函数在上不单调的充要条件，即在上有解，即可得出结论.【详解】，若在上不单调，令，则函数对称轴方程为在区间上有零点（可以用二分法求得）.当时，显然不成立；当时，只需或，解得或.故选:D.【点睛】本题考查含参数的函数的单调性及充分不必要条件，要注意二次函数零点的求法，属于中档题.8、C【解析】

由得F是弦AB的中点.进而得AB垂直于x轴，得，再结合关系求解即可【详解】因为，所以F是弦AB的中点.且AB垂直于x轴.因为以AB为直径的圆经过双曲线C的左顶点，所以，即，则，故.故选：C【点睛】本题是对双曲线的渐近线以及离心率的综合考查，是考查基本知识，属于基础题．9、B【解析】

根据程序框图列举出程序的每一步，即可得出输出结果.【详解】输入，不成立，是偶数成立，则，；不成立，是偶数不成立，则，；不成立，是偶数成立，则，；不成立，是偶数成立，则，；不成立，是偶数成立，则，；不成立，是偶数成立，则，；成立，跳出循环，输出i的值为.故选：B.【点睛】本题考查利用程序框图计算输出结果，考查计算能力，属于基础题.10、D【解析】

举例判断命题p与q的真假，再由复合命题的真假判断得答案．【详解】当时，故命题为假命题；记f（x）＝ex﹣x的导数为f′（x）＝ex，易知f（x）＝ex﹣x（﹣∞，0）上递减，在（0，＋∞）上递增，∴f（x）＞f（0）＝１＞0，即，故命题为真命题；∴是假命题故选D【点睛】本题考查复合命题的真假判断，考查全称命题与特称命题的真假，考查指对函数的图象与性质，是基础题．11、A【解析】

先分别判断每一个命题的真假，再利用复合命题的真假判断确定答案即可.【详解】当时，直线和直线，即直线为和直线互相垂直，所以“”是直线和直线互相垂直“的充分条件，当直线和直线互相垂直时，，解得.所以“”是直线和直线互相垂直“的不必要条件.：“”是直线和直线互相垂直“的充分不必要条件，故是假命题．当时，没有零点，所以命题是假命题．所以是真命题，是假命题，是假命题，是假命题．故选：．【点睛】本题主要考查充要条件的判断和两直线的位置关系，考查二次函数的图象，考查学生对这些知识的理解掌握水平.12、A【解析】

先求的展开式，再分类分析中用哪一项与相乘，将所有结果为常数的相加，即为展开式的常数项，从而求出的值.【详解】展开式的通项为，当取2时，常数项为，当取时，常数项为由题知，则.故选：A.【点睛】本题考查了两个二项式乘积的展开式中的系数问题，其中对所取的项要进行分类讨论，属于基础题.二、填空题：本题共4小题，每小题5分，共20分。13、【解析】试题分析：由已知得，故的展开式中x的奇数次幂项分别为，，，，，其系数之和为，解得．考点：二项式定理．14、【解析】

通过双曲线的标准方程，求解，，即可得到所求的结果．【详解】由双曲线，可得，，则，所以双曲线的焦点坐标是，渐近线方程为：．故答案为：；．【点睛】本题主要考查了双曲线的简单性质的应用，考查了运算能力，属于容易题．15、【解析】

由题意可得等腰三角形的两条相等的边，设，由题可得的长，在三角形中，三角形中由余弦定理可得的值相等，可得的关系，从而求出椭圆的离心率【详解】如图，若为等腰三角形，则|BF1|=|AB|.设|BF2|=t，则|BF1|=2a−t，所以|AB|=a+t=|BF1|=2a−t，解得a=2t，即|AB|=|BF1|=3t，|AF1|=2t，设∠BAO=θ，则∠BAF1=2θ，所以Г的离心率e=，结合余弦定理，易得在中，，所以，即e==，故答案为：.【点睛】此题考查椭圆的定义及余弦定理的简单应用，属于中档题.16、【解析】

首先根据定积分的应用求出的值,进一步利用二项式的展开式的应用求出结果.【详解】，根据二项式展开式通项：，令，解得，所以含的项的系数.故答案为：【点睛】本题考查定积分，二项式的展开式的应用,主要考查学生的运算求解能力,属于基础题.三、解答题：共70分。解答应写出文字说明、证明过程或演算步骤。17、（1）（2）不存在；详见解析【解析】

（1）将函数去绝对值化为分段函数的形式，从而可求得函数的最小值，进而可得m.（2）由，利用基本不等式即可求出.【详解】（1）；（2），若，同号，，不成立；或，异号，，不成立；故不存在实数，，使得，.【点睛】本题考查了分段函数的最值、基本不等式的应用，属于基础题.18、（1）详见解析；（2）详见解析.【解析】

（1）利用平行四边形的方法，证明平面.（2）通过证明平面，由此证得.【详解】（1）设是中点，连接，由于是中点，所以且，而且，所以与平行且相等，所以四边形是平行四边形，所以，由于平面，平面，所以平面.（2）连接，由于直三棱柱中，而，，所以平面，所以，由于,所以.由于四边形是矩形且，所以四边形是正方形，所以,由于,所以平面，所以.【点睛】本小题主要考查线面平行的证明，考查线面垂直的证明，考查空间想象能力和逻辑推理能力，属于中档题.19、（1）；（2）见解析.【解析】

（1）令，，利用可求得数列的通项公式，由此可得出数列的通项公式；（2）求得，利用裂项相消法求得，进而可得出结论.【详解】（1）令，，当时，；当时，，则，故；（2），.【点睛】本题考查利用求通项，同时也考查了裂项相消法求和，考查计算能力与推理能力，属于基础题.20、（1）;（2）．【解析】试题分析：（1）利用已知及平面向量数量积运算可得，利用正弦定理可得，结合，可求，从而可求的值；（2）由三角形的面积可解得，利用余弦定理可得，故可得.试题解析：（1）∵，，，∴，∴，即，又∵，∴，又∵，∴．（2）∵，∴，又，即，∴，故．21、（1）最小值为，此时；（2）见解析【解析】

（1）由已知得，法一:，，根据二次函数的最值可求得；法二:运用基本不等式构造，可得最值；法三：运用柯西不等式得：，可得最值；（2）由绝对值不等式得，，又，可得证.【详解】（1），法一:，，的最小值为，此时；法二:，，即的最小值为，此时；法三：由柯西不等式得：，,即的最小值为，此时；（2），，又，.【点睛】本题考查运用基本不等式，柯西不等式，绝对值不等式进行不等式的证明和求解