3.8-圆内接正多边形课后练习2020-2021学年-北师大版九年级下册数学-

…………○…………外…………○…………装…………○…………订…………○…………线…………○…………※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※…………○…………内…………○…………装…………○…………订…………○…………线…………○……○…………外…………○…………装…………○…………订…………○…………线…………○…………※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※…………○…………内…………○…………装…………○…………订…………○…………线…………○…………第三章圆8.圆内接正多边形课后练习2020-2021学年下学期九年级下册初中数学北师大版一、单选题（共12题）1.如图，正方形ABCD内接于⊙O，点P在AB上，则∠P的度数为（

）A.

30°

B.

45°

C.

60°

D.

90°2.⊙O是一个正n边形的外接圆，若⊙O的半径与这个正n多边形的边长相等，则n的值为（）A.

3

B.

4

C.

5

D.

63.已知圆内接正六边形的半径为2，则该内接正六边形的边心距为（

）A.

2

B.

1

C.

3

D.

324.如图，五边形ABCDE是⊙O的内接正五边形，AF是⊙O的直径，则∠BDF的度数是（

）A.

18°

B.

36°

C.

54°

D.

72°5.如图，四边形ABCD为⊙O的内接正四边形，△AEF为⊙O的内接正三角形，若DF恰好是同圆的一个内接正n边形的一边，则n的值为（

）A.

8

B.

10

C.

12

D.

156.正多边形的内切圆与外接圆的半径之比为22A.

正十二边形

B.

正六边形

C.

正四边形

D.

正三角形7.一个圆的内接正六边形与内接正方形的边长之比为（

）A.

3：2

B.

1:3

C.

1:28.正方形外接圆的半径为4，则其内切圆的半径为（

）A.

22

B.

2

C.

1

D.

229.已知正六边形ABCDEF内接于⊙O，若⊙O的直径为2，则该正六边形的周长是（

）A.

12

B.

63

C.

6

D.

10.半径为a的圆的内接正六边形的边心距是（

）A.

a2

B.

2a2

C.

3a2

11.半径为R的圆内接正三角形的面积是（

）A.

32R2

B.

πR2

C.

3312.如图，在圆内接正六边形ABCDEF中，BF，BD分别交AC于点G，H.若该圆的半径为15cm，则线段GH的长为（

）A.

5cm

B.

53cm

C.

35cm

D.

103cm二、填空题（共6题）13.如图，正五边形ABCDE内接于⊙O，点F在弧CD上，则∠BFE的度数为________14.如图，正方形ABCD和正六边形AEFCGH均内接于⊙O，连接HD；若线段HD恰好是⊙O的一个内接正n边形的一条边，则n=________．15.若圆内接正方形的边心距为3，则这个圆内接正三角形的边长为________.16.数学家刘徽首创割圆术，用圆内接正多边形的面积去无限逼近圆面积并以此求出圆周率.如图，正六边形ABCDEF的边长为2，现随机向该图形内掷一枚小针，则针尖落在阴影区域的概率为________.17.如图，正六边形ABCDEF内接于⊙O，若AB=3cm，则⊙O18.我国古代数学家刘徽创造的“割圆术”，利用了圆内接正多边形和外切正多边形的面积或周长，无限逼近圆来近似估计圆的面积或周长，从而估算出π的范围.如图1，用圆内接正方形和外切正方形周长可得22<r<4，那么利用图2中的圆内接正六边形和外切正六边形周长可进一步将π的范围缩小到________(结果保留根号)三、综合题（共4题）19.如图，已知圆O内接正六边形ABCDEF的边长为6cm，求这个正六边形的边心距n，面积S．20.如图，ABCDE是⊙O的内接正五边形．求证：AE∥BD.21.试比较图中两个几何图形的异同，请分别写出它们的两个相同点和两个不同点。例如，相同点：正方形的对角线相等，正五边形的。对角线也相等；不同点：正方形是中心对称图形，正五边形不是中心对称图形。相同点：①________；②________不同点：①________；②________.

22.求半径为3的圆的内接正方形的边长．

答案解析部分一、单选题1.【答案】B【解析】【解答】解：连接OB，OC，如图，∵正方形ABCD内接于⊙O，∴∠BOC=90°∴∠BPC=故答案为：B.【分析】根据正方形的性质可知∠BOC为90°，然后根据同圆中圆周角和圆心角的关系求∠P即可.2.【答案】D【解析】【解答】解：如图，由题意得：AB=OA=OB,∴△OAB是等边三角形，∴∠AOB=60°,

∴

正多边形的边数：n=故答案为：D.【分析】先求出△OAB是等边三角形，可得这个正多边形的中心角∠AOB=60°，据此即得结论.3.【答案】C【解析】【解答】解：如图所示圆内接正六边形ABCDEF，连结OA，OB，过O作OH⊥AB于H，∵圆内接正六边形的半径为2，∴OA=OB=2，∵∠AOB=16∴△AOB为等边三角形，∵OH⊥AB，∴OH平分∠AOB，∴∠AOH=∠HOB=12∠AOB=1所以该圆的内接正六边形的边心距OH==2×cos30°＝2×32＝3故答案为：C.【分析】连结OA，OB，过O作OH⊥AB于H，根据正六边形可得圆心角，解直角三角形即可.4.【答案】C【解析】【解答】解：∵五边形ABCDE是⊙O的内接正五边形，∴BC=DE，AC=又∵AF是⊙O的直径，∴CF=∴BF∴∠BAF=1∴∠BDF=∠BAF=54°，故答案为：C.【分析】根据正五边形的性质和圆周角定理即可得到结论.5.【答案】C【解析】【解答】解：连接OA、OD、OF，如图，∵AD，AF分别为⊙O的内接正四边形与内接正三角形的一边，∴∠AOD=360°4=90°，∠AOF=360°∴∠DOF=∠AOD-∠AOF=30°，∴n=360°30°即DF恰好是同圆内接一个正十二边形的一边.故答案为：C.【分析】连接OA、OD、OF，利用圆内接正多边形的性质可求出∠AOD和∠AOF的度数；再求出∠DOF的度数；然后用360°除以一个中心角的度数=正多边形的边数，由此可求解.6.【答案】C【解析】【解答】解：正多边形的内切圆与外接圆的半径之比为22设AB是正多边形的一边，OC⊥AB，则OC=2，OA=OB=2，在Rt△AOC中，cos∠AOC=OCAC=2∴∠AOC=45°，∴∠AOB=90°，则正多边形边数是：360°90°故答案为：C．【分析】设AB是正多边形的一边，OC⊥AB，在直角△AOC中，利用三角函数求得∠AOC的度数，从而求得中心角的度数，然后利用360度除以中心角的度数，即可求得边数．7.【答案】C【解析】【解答】解：设圆的半径为R，如图，在圆内接正方形ABCD中，OA=OB=R，∠AOB=90°，

∴圆内接正方形的边长为Rsin45°=2R.

在圆内接正六边形ABCDEF中，∠AOB=60°，

∴△AOB为等边三角形，

∴圆内接正六边形的边长为R，

∴一个圆的内接正六边形与内接正方形的边长之比为R:2R=1:2.

故答案为C.

【分析】设圆的半径为R，画出圆内接正方形以及正六边形图形，计算出圆内接正方形、内接正六边形的边长，然后作比即可.8.【答案】A【解析】【解答】解：如图所示，连接OA、OE，∵AB是小圆的切线，∴OE⊥AB，∵四边形ABCD是正方形，∴∠OAE＝45°，∴△AOE是等腰直角三角形，AE＝OE，∴OE＝22OA＝22×4＝2故答案为：A.【分析】连接OA、OE，由圆的切线垂直于过切点的半径可得OE⊥AB，由正方形的性质可得∠OAE＝45°，所以可得△AOE是等腰直角三角形，然后在等腰直角三角形AOE中用勾股定理可求解.9.【答案】C【解析】【解答】如图，连接OA、OB，∵⊙O的直径为2，∴OA=1，∵正六边形ABCDEF内接于⊙O，∴∠AOB=60°，∵OA=OB，∴△AOB是等边三角形，∴AB=OA=1，∴该正六边形的周长是1×6=6，故答案为：C.【分析】如图，连接OA、OB，由正六边形ABCDEF内接于⊙O可得∠AOB=60°，即可证明△AOB是等边三角形，根据⊙O直径可得OA的长，进而可得正六边形的周长.10.【答案】C【解析】【解答】解：如图，连接OA、OB，过点O作OH垂直AB于点H，OH即为正六边形边心距.∵六边形ABCDEF为正六边形∴∠AOB=60°，OA=OB=AB=a，AH=BH=a2∴OH=即半径为a的圆的内接正六边形的边心距是3a2.【分析】连接OA、OB，过点O作OH垂直AB于点H，OH即为正六边形边心距，根据正六边形的性质用勾股定理可求解.11.【答案】D【解析】【解答】如图所示，过O作OD⊥BC于D；∵此三角形是正三角形，∴∠BOC=360°3∵OB=OC，∴∠BOD=12∴∠OBD=30°；∵OB=R，∴OD=R2，BD=OB•cos30°=3∴BC=2BD=2×3R2=∴S△BOC=12×BC×OD=3R2×R∴S△ABC=3×3R故答案为：D．

【分析】本题的关键是用R表示出正三角形的边长，再利用正三角形的面积计算公式3412.【答案】B【解析】【解答】解：∵在圆内接正六边形ABCDEF中，AB＝AF＝BC＝CD，∠BAF＝∠ABC＝∠BCD＝120°，∴∠AFB＝∠ABF＝∠BAC＝∠ACB＝∠CBD＝∠BDC＝30°，∴AG＝BG，BH＝CH，∵∠GBH＝∠BGH＝∠BHG＝60°，∴AG＝GH＝BG＝BH＝CH，连接OA，OB角AC于N，则OB⊥AC，∠AOB＝60°，∵OA＝15cm，∴AN＝32OA＝15∴AC＝2AN＝153（cm），∴GH＝13AC＝53故答案为：B.【分析】根据正六边形的性质和等腰三角形的性质以及解直角三角形即可得到结论.二、填空题13.【答案】72°【解析】【解答】如图，连接OE、OB，∵正五边形ABCDE内接于⊙O，∴∠BOE=360°5∴∠BFE=12故答案为：72°．【分析】连接圆心和点B点E，构造圆心角，利用正五边形的性质求得圆心角的度数，从而求得∠BFE的度数即可．14.【答案】12【解析】【解答】解：如图所示，连接OA、OD、OH，∵正方形ABCD和正六边形AEFCGH均内接于⊙O，∴∠AOD=360°4∠AOH=360°6∴∠DOH=∠AOD-∠AOH=90︒-60︒=30︒，∴n=360°30°故答案为：12．【分析】先求出∠AOD=360°4=90°15.【答案】36【解析】【解答】解：正方形外接圆直径为正方形的对角线长.∵正方形边长为6，∴正方形的对角线长为62外接圆半径为32如图所示：作OD⊥BC于D，连接OB，则∠BOD=60°，在Rt△BOD中，OB=32∴BD=cos30°×OB=36∵BD=CD，∴BC=2BD=36故答案为：36【分析】

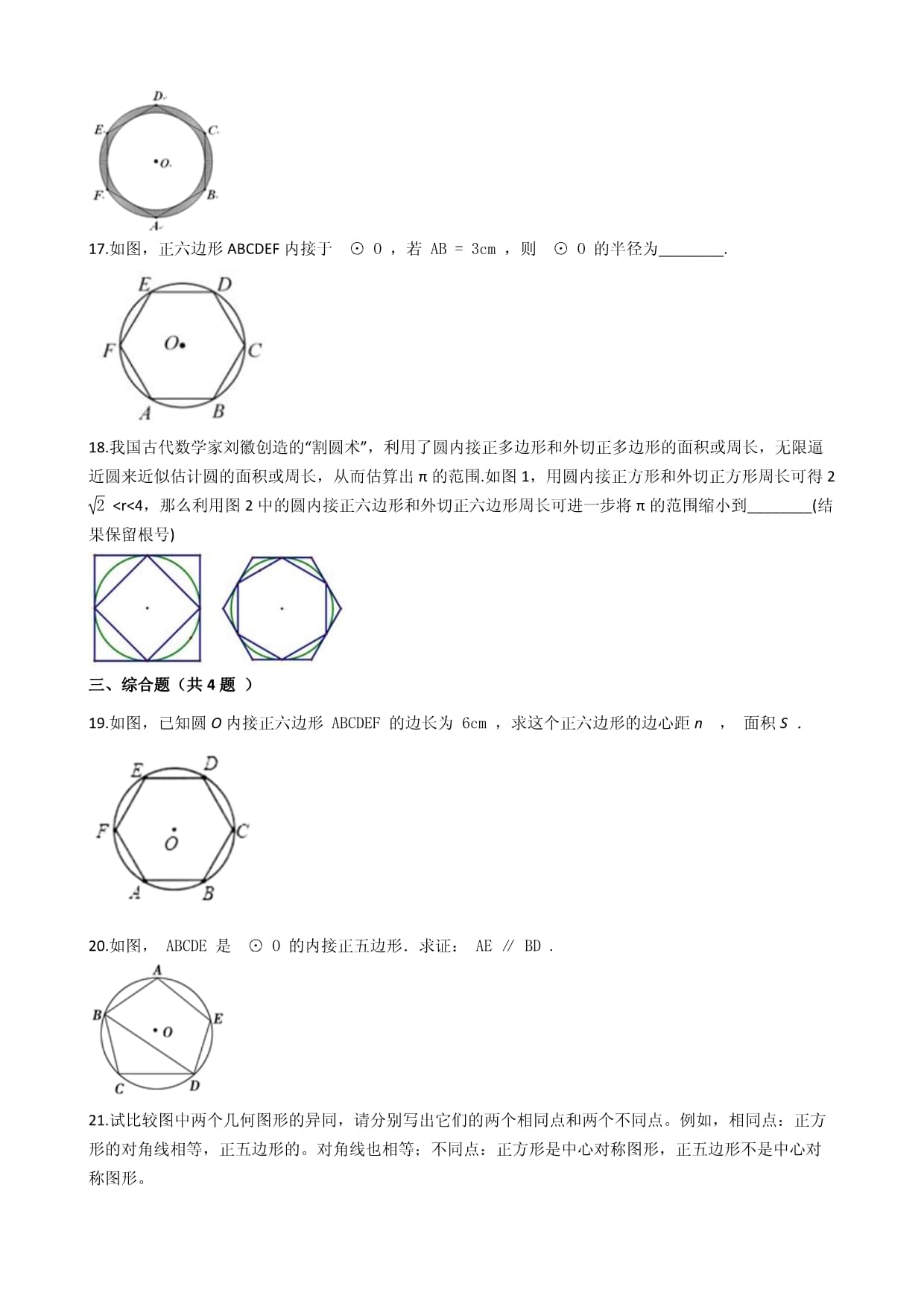
利用圆内接正方形的边心距为3，可求出正方形的边长为6，由此可求出正方形的对角线的长，根据正方形外接圆直径为正方形的对角线长，可得到外接圆的半径；作OD⊥BC于D，连接OB，可求出∠BOD的度数；然后在Rt△BOD中，利用解直角三角形求出BD的长，由此可求出这个圆的内接正三角形的边长.16.【答案】14【解析】【解答】解：设大⊙O的半径为2r，则正六边形的边长为2r，即小⊙O的半径为3r则随机向该图形内掷一枚小针，则针尖落在阴影区域的概率为π(2r)2−π故答案为：14【分析】设大⊙O的半径为2r，则正六边形的边长为2r，即小⊙O的半径为3r17.【答案】3cm【解析】【解答】解：连接OA，OB，

∵正六边形ABCDEF内接于

⊙O，

∴∠AOB=60°，

∴△AOB为等边三角形，

∴AO=AB=3cm.

故答案为：3cm.

【分析】连接OA，OB，根据题意可推出△AOB为等边三角形，然后利用等边三角形的性质解答即可.18.【答案】3<π<23【解析】【解答】解：设圆的半径为1，

∴圆的面积=2π，内接正方形周长=42，外切正方形周长=2×4=8，

∴42＜2π＜8，即2

2

<r<4，

∵内接正六边形的边长=1，外切正六边形的周长=233，

∴内接正六边形的周长=6，外切正六边形的周长=6×233=43，

∴6<2π<43，即3<π<23

;

故答案为：3<π<2三、解答题19.【答案】解：连接OA、OB，过点O作OH⊥AB于点H，即边心距n=OH，如图所示：∴AH=HB，∠AOH=BOH，∵六边形ABCDEF是正六边形，∴∠AOB