信息论与编码2016(第4章)

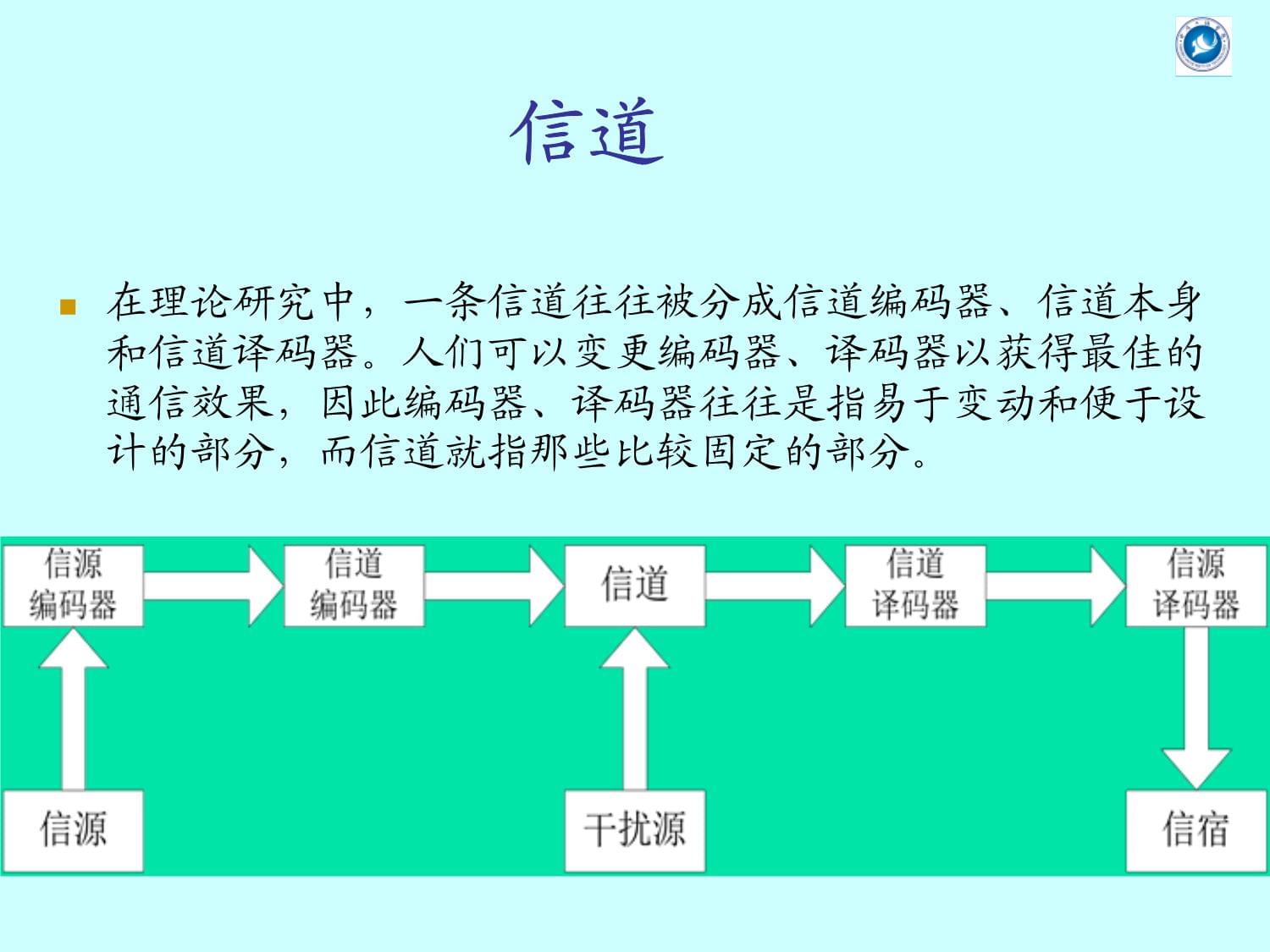
信息理论与编码朱仁祥zhurx@电子与信息工程学院1信道信道是传输信息的媒质或通道。信息是抽象的，但传送信息必须通过具体的媒质。例如二人对话，靠声波通过二人间的空气来传送，因而二人间的空气部分就是信道。邮政通信的信道是指运载工具及其经过的设施。无线电话的信道就是电波传播所通过的空间，有线电话的信道是电缆。信道在理论研究中，一条信道往往被分成信道编码器、信道本身和信道译码器。人们可以变更编码器、译码器以获得最佳的通信效果，因此编码器、译码器往往是指易于变动和便于设计的部分，而信道就指那些比较固定的部分。信道是信息论中的一个主要概念。它是用来传送信息的，所以理论上应解决信道能无错误地传送的最大信息率，也就是信道容量的计算问题，并证明这样的信息率是能达到或逼近的,最好还能知道如何实现,这就是信道编码问题。这些是山农建立信息论时提出的关于信道的理论问题。他自己回答了一些，以后许多学者又使之不断完善。一般而论，对于无记忆信道，这些问题已基本解决，但具体编码方法，如采用代数码来纠错还不能达到要求。信道第四章：信道及其容量§4.1信道分类§4.2离散无记忆信道§4.5信道的组合§4.6时间离散的无记忆连续信道§4.7波形信道5所有信道都有一个输入集A，一个输出集B以及两者之间的联系，如条件概率P(y│x)，x∈A，y∈B。这些参量可用来规定一条信道。

输入集就是信道所容许的输入符号的集。通常输入的是随机序列,随机过程在限时或限频的条件下均可化为随机序列。在规定输入集A时，也包括对各随机变量的限制,如功率限制等。输出集是信道可能输出的符号的集。输出序列可以是数或符号，也可以是一组数或矢量。

§4.1信道分类按输入集和输出集的性质，可划分为：当输入集和输出集都是离散集时，称信道为离散信道。电报信道和数据信道就属于这一类。当输入集和输出集都是连续集时，称信道为连续信道。电视和电话信道属于这一类。当输入集和输出集中一个是连续集、另一个是离散集时，则称信道为半离散信道或半连续信道。连续信道加上数字调制器或数字解调器后就是这类信道。当输入集和输出集都是连续集，输出时刻离散时，称信道为时间离散的连续信道。当输入集和输出集都是连续集，且输出时刻连续时，称信道为波形信道。§4.1信道分类根据信道的用户多少，可以分为：两端信道：它是只有一个输入端和一个输出端的单向通信的信道，它是多用户信道的基础。多端信道：当输入和（或）输出不止一个时,称为多用户信道，也就是几个用户合用一个信道。当有几个输入而输出只有一个时,习惯上称为多址接入信道。当只有一个输入，而输出有几个时,就称为广播信道。§4.1信道分类根据信道的参数与时间的关系，信道又可以分为：恒参信道：参数不随时间变化随参信道：参数随时间变化无记忆信道：信道当时的输出只依赖于当时的输入，与其它时刻的输出及输入都无关系，即P((Y1Y2…YN)=(y1y2…yN)|(X1X2…XN)=(x1x2…xN))=P(Y1=y1|X1=x1)P(Y2=y2|X2=x2)…P(YN=yN|XN=xN)。有记忆信道平稳信道：信道在不同时刻的响应特性（转移概率）是相同的，即对任意x∈{0,1,…,K-1}，y∈{0,1,…,J-1}，任意两个时刻u和v，还有P(Yu=y|Xu=x)=P(Yv=y|Xv=x)。§4.1信道分类离散无记忆平稳信道的定义信道容量的定义及定理离散无记忆平稳信道的信道容量的计算特殊的离散无记忆平稳信道－准对称信道的信道容量的计算三种特殊的准对称信道的信道容量的计算一般离散无记忆平稳信道的信道容量的计算§4.2离散无记忆信道§4.2离散无记忆信道定义4.2.1和定义4.2.2(p88)如果信道的输入为随机变量序列X1,X2,X3,…，其中每个随机变量Xu的事件集合都是{0,1,…,K-1}，信道的输出为随机变量序列Y1,Y2,Y3,…，其中每个随机变量Yu的事件集合都是{0,1,…,J-1}，则称该信道为离散信道。如果更有P((Y1Y2…YN)=(y1y2…yN)|(X1X2…XN)=(x1x2…xN))

=P(Y1=y1|X1=x1)P(Y2=y2|X2=x2)…P(YN=yN|XN=xN)，则称该信道为离散无记忆信道（DMC）。如果更有对任意x∈{0,1,…,K-1}，y∈{0,1,…,J-1}，任意两个时刻u和v，还有P(Yu=y|Xu=x)=P(Yv=y|Xv=x)，则称该信道为离散无记忆平稳信道。例：二元对称信道BSCp=0.11-p1-ppp1100当N=1时，p(0|0)=p(1|1)=0.9;p(0|1)=p(0|1)=0.1;当N=2时，p(00|00)=p(0|0)p(0|0)=p(11|11)=p(1|1)p(1|1)=0.9*0.9=0.81;p(01|00)=p(10|00)=p(01|11)=p(10|11)=0.9*0.1=0.09;p(11|00)=p(11|00)=0.1*0.1=0.01例：二元对称信道BSC§4.2离散无记忆信道一、有关DMC的信道容量设DMC在某个时刻输入随机变量为X，输出随机变量为Y。X的概率分布为{x,q(x),x∈{0,1,…,K-1}}。Y的概率分布为{y,w(y),y∈{0,1,…,J-1}}。信道响应特性为转移概率矩阵[p(y|x)，x∈{0,1,…,K-1}，y∈{0,1,…,J-1}]，它是一个K×J阶矩阵（其中p(y|x)=P(Y=y|X=x)），即§4.2离散无记忆信道因而转移概率矩阵的每一行都是一个概率向量。

若信道的输入为x，输出是哪一个符号y事先无法确定，但信道输出一定是{0,1,…,J-1}中的一个，即

§4.2离散无记忆信道对任意y∈{0,1,…,J-1}，由全概率公式有§4.2离散无记忆信道I(X;Y)是概率向量{q(x),x∈{0,1,…,K-1}}和转移概率矩阵[p(y|x)，x∈{0,1,…,K-1}，y∈{0,1,…,J-1}]的函数。

§4.2离散无记忆信道定义4.2.3(p89)离散无记忆信道的信道容量定义为：达到信道容量的输入概率分布{x,q(x),x∈{0,1,…,K-1}}称为最佳输入分布。若转移概率矩阵[p(y|x)，x∈{0,1,…,K-1}，y∈{0,1,…,J-1}]确定，如何选择概率向量{q(x),x∈{0,1,…,K-1}}使I(X;Y)达到最大？由定理2.6.2有，§4.2离散无记忆信道定理4.2.2(p91)（1）输入概率分布{x,q(x),x∈{0,1,…,K-1}}是最佳输入分布的充分必要条件为：对任何满足q(k)>0的k，都取一个相同的值；对任何满足q(k)=0的k，I(X=k;Y)都不大于此相同的值。（2）此时此相同的值恰好就是信道容量C。§4.2离散无记忆信道注解

如果对DMC信道没有任何简化，要计算最佳输入分布并不容易。但是，通常使用的DMC是很简单的（比如，以下的准对称信道和对称信道），最佳输入分布很容易求出。§4.2离散无记忆信道二、对称DMC和准对称DMC的信道容量与最佳输入分布的计算

定义4.2.4~5(p92)设DMC的转移概率矩阵为若信道转移概率矩阵所有行矢量都是第一行的置换，称信道是关于输入对称的。§4.2离散无记忆信道§4.2离散无记忆信道命题1

若DMC关于输入为对称的，则对任意k∈{0,1,…,K-1}都成立。证明{p(y|x)，y=0~J-1}与{p(y|k)，y=0~J-1}互为置换，所以对称DMC容量的计算P的所有列都是第一列的一种置换，信道是关于输出对称的§4.2离散无记忆信道§4.2离散无记忆信道命题2

若DMC关于输出为对称的，则当输入分布等概时，输出分布等概。证明此时{p(y|x)，x=0~K-1}与{p(0|x)，x=0~K-1}互为置换。设q(x)=1/K，x∈{0,1,…,K-1}。则§4.2离散无记忆信道定义4.2.6(p92)若DMC的转移概率矩阵P的列的全体可分成若干个列子集，每个列子集所对应的转移概率矩阵P的子阵都满足以下两条性质：任一行是第一行的置换，任一列是第一列的置换。则称信道为准对称信道。特别若列子集只有一个，即转移概率矩阵P本身的任一行是第一行的置换，任一列是第一列的置换，则称信道为对称信道。准对称信道对称信道§4.2离散无记忆信道几个简单的结论：（1）准对称信道一定是关于输入为对称的。（2）对称信道不仅是关于输入为对称的，也是关于输出为对称的。（3）对称DMC当输入分布等概时，输出分布等概。（4）准对称DMC当输入分布等概时，输出分布局部等概。（5）对称信道未必有J=K。§4.2

离散无记忆信道定理4.2.3实现准对称DMC信道容量的最佳输入分布为等概分布。§4.2离散无记忆信道§4.2离散无记忆信道对每个k相同值与k无关§4.2离散无记忆信道YS：子阵中每一列都是第一列置换对每个k相同值与k无关对称信道的容量计算[分析]对于行可排列情况，Hmi与i

无关[结论]例：对于二元对称信道这个式子很重要。bit/符号§4.2离散无记忆信道例4.2.3特殊的对称DMC：KSC（p93）其中0<p<1。称p为错误概率。特别当K=2时，记为BSC§4.2离散无记忆信道此时有：达到信道容量时的最佳输入分布为等概分布；对应的输出分布也是等概分布；信道容量是转移概率矩阵任何一行所对应的半平均互信息量，即§4.2

离散无记忆信道§4.2离散无记忆信道

其中0≤p<1，0≤q<1。“？”表示当我们对接收符号不能做出肯定或否定判决时，引入的删除符号，表示对该符号有疑问，可作为有误或等待更多信息时再进行判决。当q=0时，2元对称删除信道就成为BSC。当p=0时，2元对称删除信道就成为2元纯删除信道。例4.2.4特殊的准对称DMC：2元对称删除信道（p94）输入事件集为{0，1}；输出事件集为{0，？，1}；转移概率矩阵为达到信道容量时的最佳输入分布为等概分布,即p(x=0)=p(x=1)=0.5；此时输出概率分布为

p(y=0)=p(x=0)p(0|0)+p(x=1)p(0|1)=(1-q)/2类似地有p(y=1)=p(x=0)p(1|0)+p(x=1)p(1|1)=(1-q)/2p(y=?)=p(x=0)p(?|0)+p(x=1)p(?|1)=q§4.2离散无记忆信道而信道容量是转移概率矩阵任何一行所对应的半平均互信息量。§4.2离散无记忆信道当p=0时，§4.2离散无记忆信道

定义4.2.7特殊的对称DMC：模K加性噪声信道。输入随机变量为X＝{0,1,…,K-1}；噪声随机变量为Z＝{0,1,…,K-1}；输出随机变量为Y＝{0,1,…,K-1}；X与Z相互独立；Y=X+Z(modK)。称此DMC为模K加性噪声信道。§4.2离散无记忆信道此时，p(y|x)=P(Y=y|X=x)=P(X+Z(modK)=y|X=x)=P(x+Z(modK)=y|X=x)=P(Z=y-x(modK)|X=x)=P(Z=y-x(modK))。这就是说，如果记P(Z=z)=sz，则转移概率矩阵为§4.2离散无记忆信道显然模K加性噪声信道是对称DMC，达到信道容量时的最佳输入分布为等概分布，对应的输出分布也是等概分布。三、一般DMC的信道容量与最佳输入分布的计算

若DMC的转移概率矩阵是可逆方阵，则可以先假设最佳输入分布{q(x),x∈{0,1,…,K-1}}中每个概率q(x)都满足q(x)>0。在这个假设下，求出信道容量C；

注意：这个解是否成立需要验证，即由信道容量C，计算对应的最佳输入分布，若每个q(x)都是概率矢量，所得到的解就是正确的；否则，解就是不正确的，这时应令某个q(x),为0，再进行试算，有时需要令一个以上q(x),为0试解，这时就出现J>K的情况，在求解时变元个数大于方程数，可能有多个解，但只有一个解满足条件，这时求解信道容量的问题就变成一组非线性方程组求解问题，即使得到解，也有可能有某些小于0，要找到最佳分布是相当困难的。§4.2离散无记忆信道具体地验算过程为：先利用求出的信道容量C，计算最佳输入分布对应的“最佳输出分布”{w(y),y∈{0,1,…,K-1}}；随后计算出最佳输入分布{q(x),x∈{0,1,…,K-1}}。§4.2离散无记忆信道§4.2离散无记忆信道§4.2离散无记忆信道§4.2离散无记忆信道§4.2离散无记忆信道这是K个未知量{β0,β1,…,βK-1}={C+logw(0),C+logw(1),…,C+logw(K-1)}的线性方程组，系数矩阵是可逆方阵，因此唯一解出{β0,β1,…,βK-1}为§4.2离散无记忆信道求出了{β0,β1,…,βK-1}={C+logw(0),C+logw(1),…,C+logw(K-1)}，还不能确定C和{w(0),w(1),…,w(K-1)}的值。但是我们还有另一个等式：

w(0)+w(1)+…+w(K-1)=1。于是§4.2离散无记忆信道求出了信道容量C，立即得到了“最佳输出分布”{w(y),y∈{0,1,…,K-1}}和对应的最佳输入分布{q(x),x∈{0,1,…,K-1}}。§4.2离散无记忆信道例特殊的DMC，称为Z信道：输入事件为{0,1}，输出事件为{0,1}，转移概率矩阵为其中0<ε<1。求信道容量和最佳输入分布。先假设最佳输入分布{q(0),q(1)}满足q(0)>0，q(1)>0。因此§4.2离散无记忆信道容易验证：q(1)>0；

q(0)+q(1)=1。需要验证：q(0)>0。§4.2离散无记忆信道例设DMC的输入事件为{0,1}，输出事件为{0,1}，转移概率矩阵为求信道容量和最佳输入分布。先假设最佳输入分布{q(0),q(1)}满足q(0)>0，q(1)>0。因此§4.2离散无记忆信道因此§4.5信道的组合总设有如下两个相互独立的DMC，分别称为信道1和信道2。信道1的输入事件为全体x，共有K个输入事件；信道1的输出事件为全体y，共有J个输出事件；信道1的转移概率矩阵为[p1(y|x)]K×J；信道1的信道容量为C1,达到信道容量的最佳输入分布为q1(x)。信道2的输入事件为全体u，共有N个输入事件；信道2的输出事件为全体v，共有M个输出事件；信道2的转移概率矩阵为[p2(v|u)]N×M；信道2的信道容量为C2,达到信道容量的最佳输入分布为q2(u)。积信道待发送的消息比较多时，可能会使用信道1和信道2同时分别传递消息，则称该信道为信道1与信道2的积信道。（又称为信道1与信道2的独立并行信道）。此时对于组合信道输入集X=X1×X2,输出集Y=Y1×Y2,转移概率p(jj’|kk’)=p(j|k)p(j’|k’)信道1P(j|k)X1Y1信道2P(j‘|k’)X2Y2例：设有如下两个相互独立的DMC，求积信道的转移概率矩阵。积信道解：组合后的积信道的输入集有4个元素；输出集也有4个元素；求积信道的转移概率矩阵P为：§4.5信道的组合定理4.5.1（p104）积信道的信道容量为C=C1+C2,最佳输入分布为q1(x)q2(u).证明此时§4.5信道的组合§4.5信道的组合§4.5信道的组合所以I((XU)=(xu);(YV))=I(X=x;Y)+I(U=u;V)。注意到对任何满足q1(x)>0的x，I(X=x;Y)=C1；对任何满足q1(x)=0的x，I(X=x;Y)≤C1；对任何满足q2(u)>0的u，I(U=u;V)=C2

；对任何满足q2(u)=0的u，I(U=u;V)≤C2。于是对任何满足q1(x)q2(u)>0的(xu)，I((XU)=(xu);(YV))=C1+C2

；对任何满足q1(x)q2(u)=0的(xu)，I((XU)=(xu);(YV))≤C1+C2

。根据定理4.2.2(p84)，积信道的信道容量为C=C1+C2。§4.5信道的组合定义4.5.2（p106）单位时间内可随机选用信道1和信道2中的一个，选用信道1的概率为p1，选用信道2的概率为p2，p1+p2=1信道的输入事件为全体{x}∪{u}，其中{x}与{u}不相交；共有K+N个输入事件；信道的输出事件为全体{y}∪{v}，其中{y}与{v}不相交；共有J+M个输出事件；信道的转移概率矩阵为则称该信道为信道1与信道2的和信道。§4.5信道的组合定理4.5.2（p106）§4.5信道的组合证明：§4.5信道的组合§4.5信道的组合§4.5信道的组合定义4.5.3（p106）构造一个信道，使得该信道的输入是信道1的输入；信道1的输出再输入信道2；信道2的输出就是该信道的输出。则称该信道为信道1与信道2的级连信道（串联信道）。请注意：此时信道1的输出事件全体恰好是信道2的输入事件全体，即{y}={u}，J=N。§4.5信道的组合注：（1）级连信道的转移概率矩阵为[p(v|x)]K×M=[p1(y|x)]K×J[p2(v|y)]J×M，即§4.5信道的组合例设信道1的转移概率矩阵为其中0<p<1。则（1）信道1的最佳输入分布是等概分布，信道容量为§4.5信道的组合（2）将信道1自级连N次，级连信道的转移概率矩阵为级连信道的信道容量为§4.5信道的组合（3）令自级连的次数N→+∞，则级连信道的转移概率矩阵趋向于信道容量趋向于0。§4.6时间离散的无记忆连续信道定义设信道的输入为随机变量序列X1,X2,X3,…，其中每个随机变量Xu都是连续型的随机变量。信道的输出为随机变量序列Y1,Y2,Y3,…，其中每个随机变量Yu都是连续型的随机变量。转移概率密度f((Y1

Y2…YN)=(y1y2…yN)|(X1

X2…XN)=(x1x2…xN))=f(Y1=y1|X1=x1)f(Y2=y2|X2=x2)…f(YN=yN|XN=xN)，则称该信道为时间离散的无记忆连续信道。如果进一步有f(Yn=y|Xn=x)=f(Ym=y|Xm=x),则称该信道为平稳的（恒参的）时间离散的无记忆连续信道。§4.6时间离散的无记忆连续信道设平稳的（恒参的）时间离散的无记忆连续信道，其一元转移概率密度为fY|X(y|x)。设一元输入概率密度为fX(x)。因此一元输出概率密度为如下的fY(y)，输入、输出平均互信息量为如下的I(X;Y)。§4.6时间离散的无记忆连续信道一、可加噪声信道定义4.6.1（p108）设平稳的（恒参的）时间离散的无记忆连续信道为：输入随机变量为X；噪声随机变量为Z；X与Z相互独立；输出随机变量为Y=X+Z。则称该信道为可加噪声信道。注：此时fY|X(y|x)=f(Y=y|X=x)=f(X+Z=y|X=x)=f(x+Z=y|X=x)=f(Z=y-x|X=x)=f(Z=y-x)=fZ(y-x)；f

(X,Y)(x,y)=fX(x)fY|X(y|x)=fX(x)fZ(y-x)；§4.6时间离散的无记忆连续信道作变元替换，令z=y-x§4.6时间离散的无记忆连续信道例4.6.1（p108）高斯可加噪声信道，当信道干扰给定时，若输入功率不受限制，I(X;Y)可为任意大均值为零的正态分布其方差为该信号的平均功率§4.6时间离散的无记忆连续信道二、平均功率受限的可加噪声信道定义（p109的变形）对于可加噪声信道，限定：其信号功率不超过S，其噪声功率等于σ2，此时信噪比不超过(S/σ2)。在此限定之下，输入、输出平均互信息量的最大值C称为平均功率受限的信道容量。§4.6时间离散的无记忆连续信道定理4.6.1（p109）设可加噪声信道，限定：其信号功率不超过S，其噪声功率为σ2，此时信噪比不超过(S/σ2)。则（1）平均功率受限的信道容量为（2）当且仅当信道为高斯可加噪声信道（X~N(λ,S)，Z~N(μ,σ2)）时，输入、输出平均互信息量达到该C。§4.7波形信道定义4.7.1（p112）信道的输入是一般的随机过程{X(t),t≥0}；信道的输出是一般的随机过程{Y(t),t≥0}。称此信道为波形信道（waveformchannel）

。定义4.7.2（p112）信道的输入是一个随机过程