《多自由度自由振动》课件

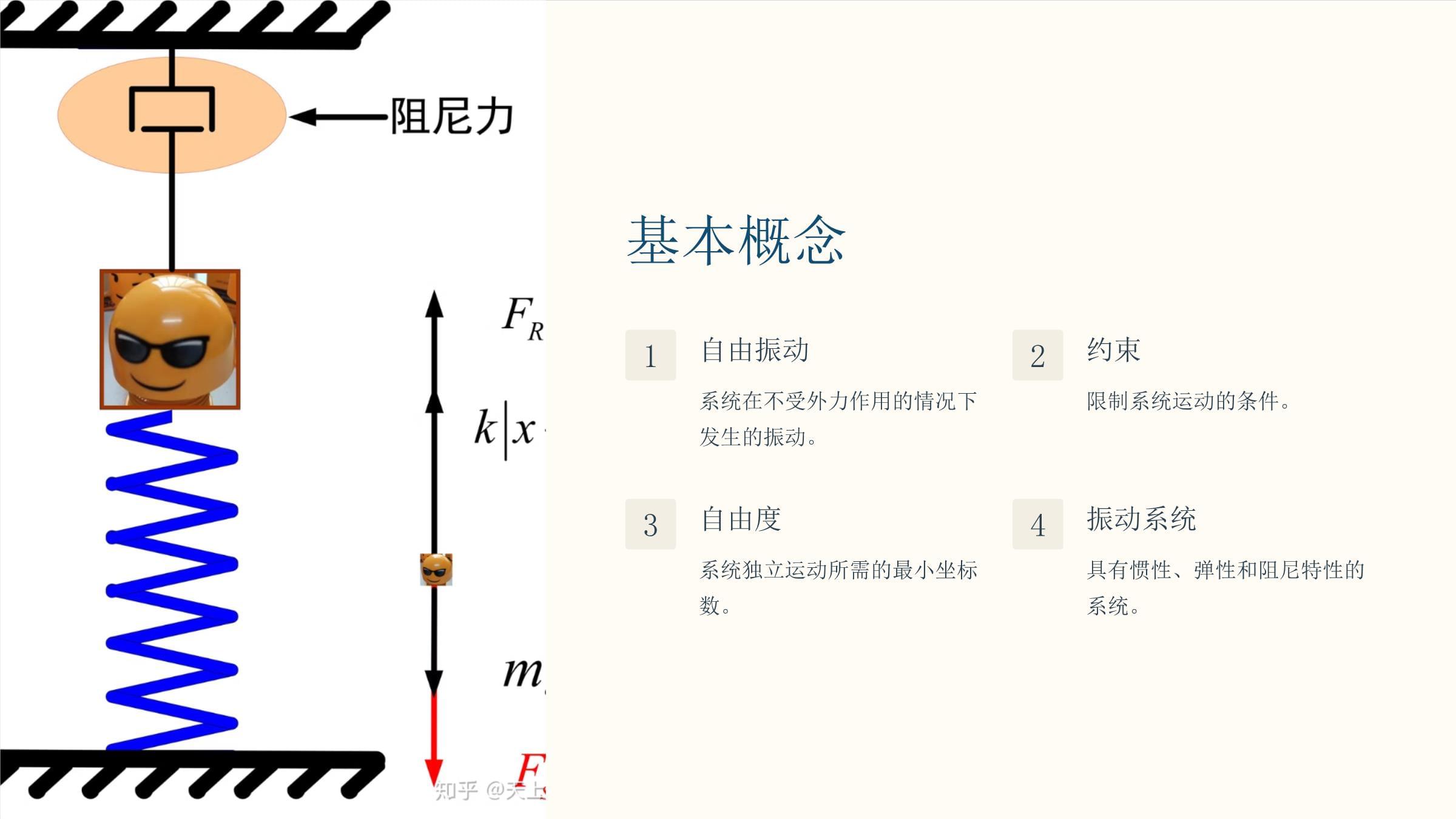
多自由度自由振动多自由度自由振动是指系统具有多个独立运动自由度的振动现象。例如，一个弹簧-质量系统，如果有多个质量块和弹簧相互连接，则该系统具有多个自由度。课程目标理解多自由度振动掌握多自由度振动系统基本概念掌握求解方法能运用微分方程和矩阵方法求解振动问题应用于工程实践分析实际工程结构的振动特性基本概念1自由振动系统在不受外力作用的情况下发生的振动。2约束限制系统运动的条件。3自由度系统独立运动所需的最小坐标数。4振动系统具有惯性、弹性和阻尼特性的系统。牛顿第二定律作用力与加速度物体所受的合外力与其质量乘以加速度的乘积相等。方向一致合外力与加速度的方向总是保持一致。力的作用力的作用会改变物体的运动状态，使其加速或减速。自由振动微分方程1牛顿第二定律F=ma2运动方程基于牛顿定律3微分方程描述自由振动自由振动微分方程是描述系统在不受外力作用下的运动规律。这些方程通常由牛顿第二定律推导而来，并基于系统的质量、弹性系数和阻尼系数等参数。特殊解简谐振动自由度系统中，每个坐标都以正弦或余弦函数形式振动。频率振动系统每个坐标的振动频率相同，称为系统的固有频率。相位每个坐标的振幅和相位可能不同，取决于系统的初始条件。特殊解讨论特殊解是振动系统的一种特定状态，它只包含一个振动频率，即系统的固有频率。特殊解的振动幅度通常由系统的初始条件决定。在实际应用中，我们通常会使用特殊解来分析系统的振动特性，例如，我们可能会使用特殊解来确定系统的固有频率和阻尼比。一自由度自由振动1基本概念单摆是典型的自由振动系统，其运动受重力势能控制，在无外力的情况下，单摆将以固有频率进行往复运动。2自由振动方程用牛顿第二定律可推导出自由振动的微分方程，该方程描述了振动系统的位置、速度和加速度随时间变化的关系。3振动周期与频率自由振动的周期取决于振动系统的固有频率，固有频率由系统的质量和弹性系数决定，且与振幅无关。一自由度振型与频率振型频率描述系统运动的形状系统振动的速度由固有频率决定与系统的质量和刚度有关阻尼振动阻尼振动介绍阻尼振动是指振动系统在振动过程中，由于受到阻尼力的影响而逐渐衰减的振动。阻尼力是指阻碍振动系统振动的力，例如摩擦力、空气阻力、粘性阻力等。阻尼振动的类型阻尼振动可以分为两种类型：粘性阻尼和库仑阻尼。粘性阻尼是指阻尼力的大小与振动速度成正比，例如液体中的阻力。库仑阻尼是指阻尼力的大小与振动速度无关，例如固体之间的摩擦力。阻尼振型与频率阻尼的存在改变了系统的振动行为，引入阻尼将导致振幅随时间衰减，并影响系统的固有频率。1频率降低阻尼会降低系统的固有频率。2振幅衰减阻尼会使振动幅度随时间逐渐减小。3临界阻尼临界阻尼是指使系统在最短时间内回到平衡状态的阻尼值。4过阻尼过阻尼是指阻尼值大于临界阻尼值，系统不会发生振动，而是缓慢地回到平衡状态。二自由度自由振动1运动方程自由振动下，两个自由度振动系统2振动模式根据振动频率，系统表现出不同的运动模式3频率解求解特征值，获得系统的自然频率4振型解根据特征向量，确定振动时的相对位移二自由度振动系统比一自由度系统更复杂，系统表现出不同的振动模式，通过求解特征值和特征向量，可以确定系统的自然频率和振型。二自由度振型与频率二自由度系统有两种振动模式，分别对应着不同的振动频率。第一种模式是两个质量同时以相同方向振动，被称为同相振动。第二种模式是两个质量以相反方向振动，被称为反相振动。每个振动模式都有一个特定的频率，称为固有频率。二自由度系统的振动频率取决于两个质量的质量、弹簧的刚度和阻尼系数。通过改变这些参数，可以改变系统的振动频率。在实际应用中，可以通过改变系统的参数来调整系统的振动特性，例如，通过增加质量来降低振动频率。质量耦合二自由度11.质量耦合当两个质量之间存在直接的质量耦合时，它们会相互影响，改变彼此的振动模式。22.振动模式质量耦合会导致系统出现两种不同的振动模式，其中一个质量可能振动得更剧烈，而另一个质量则振动得更轻微。33.振动频率质量耦合会导致系统的振动频率发生变化，两个质量的振动频率不再相同，而是会受到彼此的影响。44.振动响应质量耦合会改变系统对外部激励的响应，系统的振动响应会更加复杂，也更难预测。刚度耦合二自由度刚度耦合两个振动系统通过弹簧连接，构成刚度耦合系统。刚度耦合系统中，两个质量块的运动相互影响。振动方程设两个质量块的质量分别为m1和m2，弹簧的劲度系数分别为k1和k2。根据牛顿第二定律，可以得到二自由度振动系统的运动方程。刚度耦合二自由度概述刚度耦合二自由度系统中，两个振动系统通过弹性元件连接。弹性元件的刚度影响系统间的相互作用，导致耦合运动。耦合运动刚度耦合导致两个系统无法独立振动，而是相互影响，表现出耦合运动，即振动频率和振幅相互影响。典型例子典型的例子包括双摆系统，两个摆通过弹簧连接，一个摆的振动会影响另一个摆的振动。应用场景刚度耦合系统在桥梁、建筑物、机械设备等领域广泛存在，了解耦合运动规律对于结构设计和振动控制至关重要。多自由度振型与频率多自由度系统可以有多种振动模式，每种模式都有其独特的振型和频率。振型是系统在特定频率下振动的形状，频率是系统振动的快慢。对于多自由度系统，每个振型都对应一个唯一的频率，每个频率对应一个振型。例如，对于一个有两个自由度的系统，可能会有两个振型，每个振型对应一个不同的频率。一个振型可能对应一个较低的频率，另一个振型可能对应一个较高的频率。每个振型和频率都是系统固有特性，并且可以用来预测系统的振动响应。广义坐标与广义力广义坐标广义坐标是用来描述系统运动状态的一组独立坐标，这些坐标可以是直角坐标、极坐标、角度或其他任何描述系统位置的量。它们可以简化振动问题的求解。广义力广义力对应于广义坐标，它反映了外力对系统所做的功，它可以是实际的力或力矩，也可以是其他物理量，如势能或能量。简化模型广义坐标与广义力将复杂的振动系统简化为更容易分析的模型，可以帮助我们更好地理解系统的运动规律。广义坐标下的振动方程1定义用广义坐标表示系统运动状态2方程将拉格朗日方程应用于广义坐标3求解得到系统在广义坐标下的振动方程广义坐标是描述系统运动状态的独立变量，可以是系统的位移、角度、速度等。使用广义坐标建立振动方程可以简化分析过程，并方便求解系统的振动特性。正交振型相互垂直振型之间相互垂直，体现了振动的独立性。能量守恒振型正交确保了系统能量在不同振型之间不会相互转换。模态分析正交振型是模态分析的基础，为理解复杂结构的振动特性提供关键信息。正交振型的求解1建立振动方程利用牛顿第二定律或拉格朗日方程2求解特征值特征值对应系统固有频率3求解特征向量特征向量对应振动模态4正交化确保振型相互独立正交振型的求解过程包含多个步骤，首先需要建立振动方程，利用牛顿第二定律或拉格朗日方程来描述系统的运动规律。然后，求解特征值和特征向量，特征值代表系统的固有频率，特征向量则代表振动模态。最后，需要对振型进行正交化，以确保各个振型相互独立。大型结构的振型分析建筑结构分析高层建筑的振型，确保建筑安全稳定，抵抗风力、地震等外力影响。桥梁结构研究桥梁的振型，确定最佳结构设计，防止共振现象，确保桥梁安全运行。大型风机结构分析风力发电机的振型，优化设计叶片和塔架，提高发电效率和稳定性。实例分析一该实例分析将展示多自由度自由振动的实际应用。我们会以一个常见的工程结构为例，并通过具体的计算和分析，揭示多自由度振动理论在工程实践中的重要意义。通过分析该实例，我们可以更直观地理解多自由度振动系统中振型的概念、频率特性以及振动模式之间的关系。此外，我们将探讨如何利用多自由度振动理论来预测结构的振动行为，并采取有效的措施来控制振动，避免结构共振带来的风险。实例分析二考虑一个由若干杆件组成的桁架结构，每个节点处都有质量集中。可以根据其几何形状和杆件的刚度建立多自由度振动模型。通过求解特征值问题，得到结构的固有频率和振型。了解结构的振动特性，可以帮助我们进行抗震设计和疲劳分析。实例分析三实例分析三，以一个多层建筑为例，该建筑的楼层数量为5层，每层楼板的质量为1000kg，楼板的弹性模量为20GPa，剪切模量为8GPa，楼层高度为3m。使用有限元软件对建筑结构进行建模，并进行模态分析，得到建筑结构的前三阶振型和频率。实例分析四本实例展示了多自由度振动分析在实际工程中的应用。我们以一座混凝土桥梁为例，该桥梁跨越河流，并承受交通载荷。通过多自由度振动分析，我们可以计算出桥梁的固有频率和振型，从而评估其在不同载荷下的振动特性。根据分析结果，我们可以