福建省龙岩市连城县第三中学2022-2023学年高一数学文期末试卷含解析

福建省龙岩市连城县第三中学2022-2023学年高一数学文期末试卷含解析一、选择题：本大题共10小题，每小题5分，共50分。在每小题给出的四个选项中，只有是一个符合题目要求的1.如图.五角星魅力无穷,移动点由A处按图中数字由小到大的顺序依次运动,当第一次结束回到A处时,数字为6,按此规律无限运动,则数字2010应在

A.B处

B.C处

C.D处

D.E处参考答案：D略2.已知，，，若，则等于（

）A. B. C. D.参考答案：A【分析】根据向量的坐标运算法则,依据题意列出等式求解.【详解】由题知:,,,因为,所以,故,故选:A.【点睛】本题考查向量的坐标运算,属于基础题.3.函数y=ax﹣2（a＞0，a≠1）的图象必经过点（）A．（0，1） B．（1，1） C．（2，0） D．（2，1）参考答案：D【考点】指数函数的单调性与特殊点．【分析】根据指数函数y=ax过定点（0，1）的性质，即可推导函数y=ax﹣2（0＜a≠1）的图象过定点（2，1）．【解答】解：∵指数函数y=ax过定点（0，1），∴将y=ax向右平移2个单位，得到y=ax﹣2，则函数y=ax﹣2（0＜a≠1）的图象过定点（2，1）．故选：D4.设，，，则A．

B．

C．

D．参考答案：C5.已知A={α|α=k×45°+15°，k∈Z}，当k=k0（k0∈Z）时，A中的一个元素与角﹣255°终边相同，若k0取值的最小正数为a，最大负数为b，则a+b=（）A．﹣12 B．﹣10 C．﹣4 D．4参考答案：C【考点】终边相同的角．【分析】写出与角﹣255°终边相同的角的集合，求出最小正角与最大负角，结合集合A的答案．【解答】解：与角﹣255°终边相同的角的集合为{β|β=n×360°﹣255°，n∈Z}，取n=1时，β=105°，此时A={α|α=k×45°+15°，k∈Z}中的k0取最小正值为2；取n=0时，β=﹣255°，此时A={α|α=k×45°+15°，k∈Z}中的k0取最大负值为﹣6．∴a+b=2﹣6=﹣4．故选：C．6.已知函数，函数的值域是（

）A.[0，2)

B.(0,+∞)

C.(0，2)

D.[0,+∞)参考答案：C7.若偶函数f（x）在（﹣∞，﹣1]上是增函数，则下列关系式中成立的是（）A．f（﹣）＜f（﹣1）＜f（2） B．f（﹣1）＜f（﹣）＜f（2） C．f（2）＜f（﹣1）＜f（﹣） D．f（2）＜f（﹣）＜f（﹣1）参考答案：D【考点】奇偶性与单调性的综合．【专题】常规题型．【分析】题目中条件：“f（x）为偶函数，”说明：“f（﹣x）=f（x）”，将不在（﹣∞，﹣1]上的数值转化成区间（﹣∞，﹣1]上，再结合f（x）在（﹣∞，﹣1]上是增函数，即可进行判断．【解答】解：∵f（x）是偶函数，∴f（﹣）=f（），f（﹣1）=f（1），f（﹣2）=f（2），又f（x）在（﹣∞，﹣1]上是增函数，∴f（﹣2）＜f（﹣）＜f（﹣1）即f（2）＜f（﹣）＜f（﹣1）故选D．【点评】本小题主要考查函数单调性的应用、函数奇偶性的应用、奇偶性与单调性的综合等基础知识，考查运算求解能力、化归与转化思想．属于基础题．8.用单位正方块搭一个几何体，使它的主视图和俯视图如右图所示，则该几何体的体积的最小值与最大值分别为（

）A．与

B．与

C．与

D．与

参考答案：C略9.已知集合,集合,则=（

）A.

B.

C.

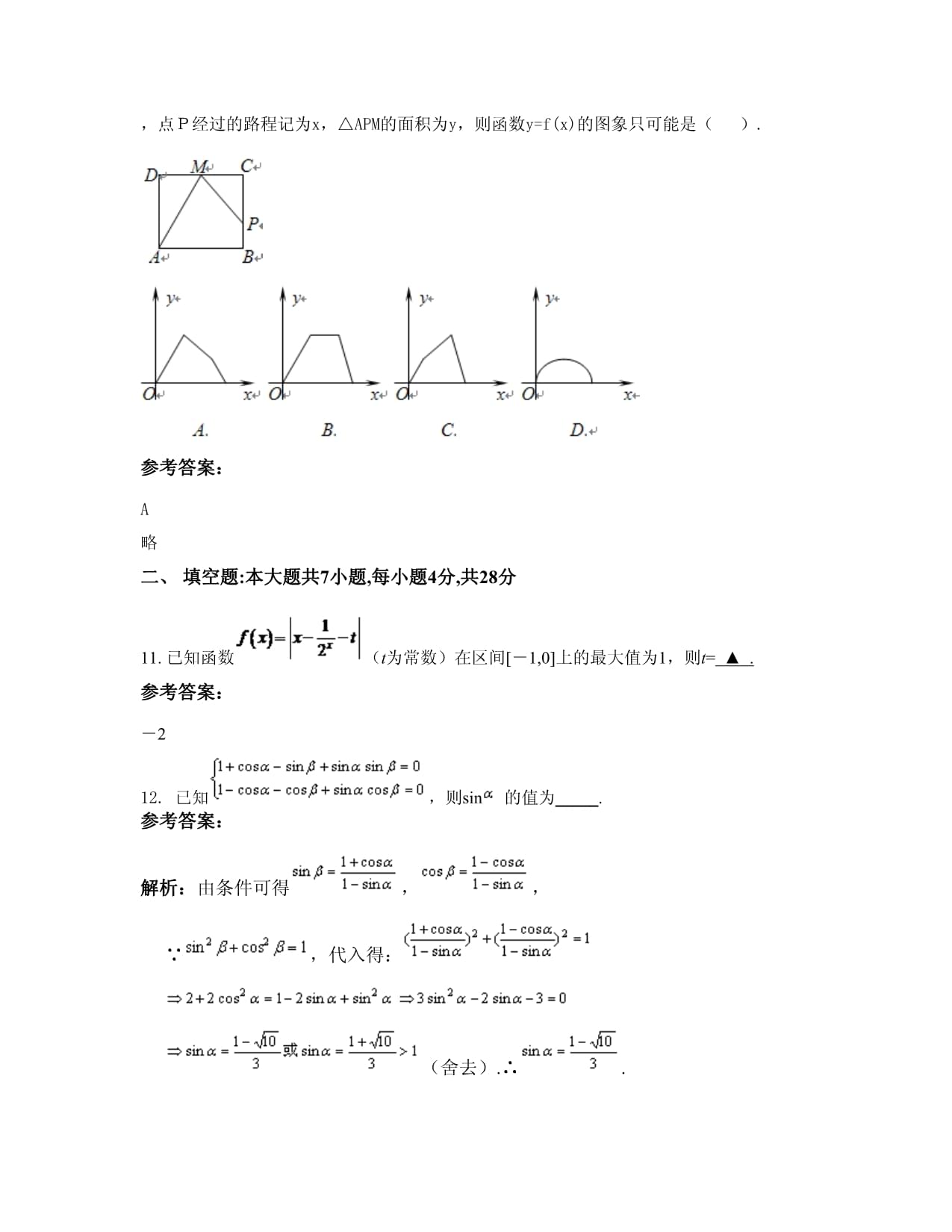
D.参考答案：A10.如图，点P在边长为1的正方形ABCD边上运动，设点M是CD边的中点，点P沿A?B?C?M运动时，点Ｐ经过的路程记为x，△APM的面积为y，则函数y=f(x)的图象只可能是（

）.参考答案：A略二、填空题:本大题共7小题,每小题4分,共28分11.已知函数（t为常数）在区间[－1,0]上的最大值为1，则t=

▲

.参考答案：－212.已知，则sin的值为_____.参考答案：解析：由条件可得，，∵，代入得：（舍去）.∴.13.设函数若，则

．参考答案：略14.是第三象限的角，并且，则的值是

▲

参考答案：略15.设数列中，，，，则通项

参考答案：由已知有所以16.已知与之间的一组数据为则与的回归直线方程为__

参考答案：略17.已知向量的夹角为，，则___________．参考答案：试题分析：，，所以，提醒：．考点：平面向量数量积的应用之一：求模．三、解答题：本大题共5小题，共72分。解答应写出文字说明，证明过程或演算步骤18.已知等差数列的前项和为()，，．（1）求数列的通项公式；（2）设，求；（3）若数列满足，求的最小值及此时的值.参考答案：略19.已知数列{an}满足，且．（1）求及an．（2）设，求数列{bn}的前n项和Sn．参考答案：（1）2，；（2）.【分析】（1）根据题意知数列是等比数列，代入公式得到答案.（2）先把表示出来，利用分组求和法得到答案.【详解】解：（1）因为，所以数列是以首项为2，公比为3的等比数列，所以数列；（2）==.【点睛】本题考查了等比数列的通项公式和分组求和法，是数列的常考题型.20.已知双曲线的中心在原点，焦点F1，F2在坐标轴上，一条渐近线方程为y=x，且过点（4，﹣）．（1）求双曲线方程；（2）若点M（3，m）在此双曲线上，求?．参考答案：【考点】双曲线的标准方程；直线与圆锥曲线的关系．【专题】圆锥曲线的定义、性质与方程．【分析】（1）设双曲线方程为x2﹣y2=λ，λ≠0，由双曲线过点（4，﹣），能求出双曲线方程．（2）由点M（3，m）在此双曲线上，得m=．由此能求出?的值．【解答】解：（1）∵双曲线的中心在原点，焦点F1，F2在坐标轴上，一条渐近线方程为y=x，∴设双曲线方程为x2﹣y2=λ，λ≠0，∵双曲线过点（4，﹣），∴16﹣10=λ，即λ=6，∴双曲线方程为=1．（2）∵点M（3，m）在此双曲线上，∴=1，解得m=．∴M（3，），或M（3，﹣），∵F1（﹣2，0），，∴当M（3，）时，=（﹣2﹣3，﹣），=（，﹣），?=﹣12﹣6=0；当M（3，﹣）时，=（﹣2﹣3，），=（，），?=﹣12﹣6+6+9+3=0．故?=0．【点评】本题考查双曲线方程的求法，考查向量的数量积的求法，解题时要认真审题，注意双曲线性质的合理运用．21.（12分）已知A（2，0），B（0，2），C（cosα，sinα）（0＜α＜π）．（1）若|+|=（O为坐标原点），求与的夹角；（2）若⊥，求tanα的值．参考答案：考点： 平面向量数量积的运算．专题： 平面向量及应用．分析： （1）由=（2+cosα，sinα），利用向量模的计算公式可得（2+cosα）2+sin2α=7，化简整理可得，又0＜α＜π，即可解得α．设与的夹角为θ，θ∈．利用向量夹角公式即可得出．（2），可得=0，cosα+sinα=，又sin2α+cos2α=1，联立解得即可．解答： （1）由=（2+cosα，sinα），|+|=，∴（2+cosα）2+sin2α=7，∴4+4cosα+cos2α+sin2α=7，化为，又0＜α＜π，解得．∴=，设与的夹角为θ，θ∈．则cosθ==，∴．即与的夹角为．（2）∵=（cosα﹣2，sinα），=（cosα，sinα﹣2）．∵⊥，∴=cosα（cosα﹣2）+sinα（sinα﹣2）=1﹣2cosα﹣2sinα=0，∴cosα+sinα=，又sin2α+cos2α=1，∵0＜α＜π，联立解得，．∴==﹣．点评： 本题考查了向量模的计算公式、向量夹角公式、向量垂直与数量积的关系、同角三角函数基本关系式，考查了推理能力与计算能力，属于中档题．22.如图，三四棱锥P﹣ABCD中，侧面PAD⊥底面ABCD，侧棱PA=PD=，底面ABCD为直角梯形，其中BC∥AD，AB⊥AD，AD=2AB=2BC=2．（1）求异面直线PB与CD所成角的余弦值；（2）线段AD上是否存在Q，使得它到平面PCD的距离为？若存在，求出的值；若不存在，请说明理由．参考答案：【考点】异面直线及其所成的角；棱锥的结构特征．【分析】（1）取AD中点O，连接PO，BO，证明OBCD是平行四边形，可得OB∥DC，在证明PO⊥平面ABCD，∠POB是异面直线PB与CD所成的角，利用Rt△POA即可求解．（2）假设存在点Q，使得它到平面的距离为．设QD=x，则，利用VP﹣DQC=VQ﹣PCD求解x的值，即可得到的值．【解答】解：（1）设O为AD中点，连接PO，BO，在直角梯形ABCD中，BC∥AD，AD=2AB=2BC，有OD∥BC且OD=BC，∴四边形OBCD是平行四边形，所以OB∥DC，在△PAD中PA=PD，O为AD中点，∴PO⊥AD．侧面PAD⊥底面ABCD，平面PAD∩平面ABCD=AD，PO?平面PAD，∴PO⊥平面A