三视图中的小正方体计数问题

三视图中的小正方体计数问题通过小正方体组合图形的三视图，拟定组合图形中小正方体的个数，在中考或竞赛中经常会碰到。解决这类问题如果没有掌握对的的办法，仅仅依赖空间想象去解决，不仅思维难度很大，还很容易出错。

通过三视图计算组合图形的小正方体的个数，核心是要搞清晰这个小正方体组合图形共有多少行、多少列、每行每列中各有多少层，理清了这些行、列、层的数量，小正方体的个数就迎刃而解了。在三视图中，通过主视图、俯视图能够拟定组合图形的列数；通过俯视图、左视图能够拟定组合图形的行数；通过主视图、左视图能够拟定行与列中的最高层数。

以上办法可简要地概括为：“主俯看列，俯左看行，主左看层，分清行列层，计数不求人。”

一、成果唯一的计数

例1在一仓库里堆放着若干个相似的正方体货箱，仓库管理员将这堆货箱的三视图画了出来，如图所示，则这堆正方体货箱共有（

）A．9箱

B．10箱

C．11箱

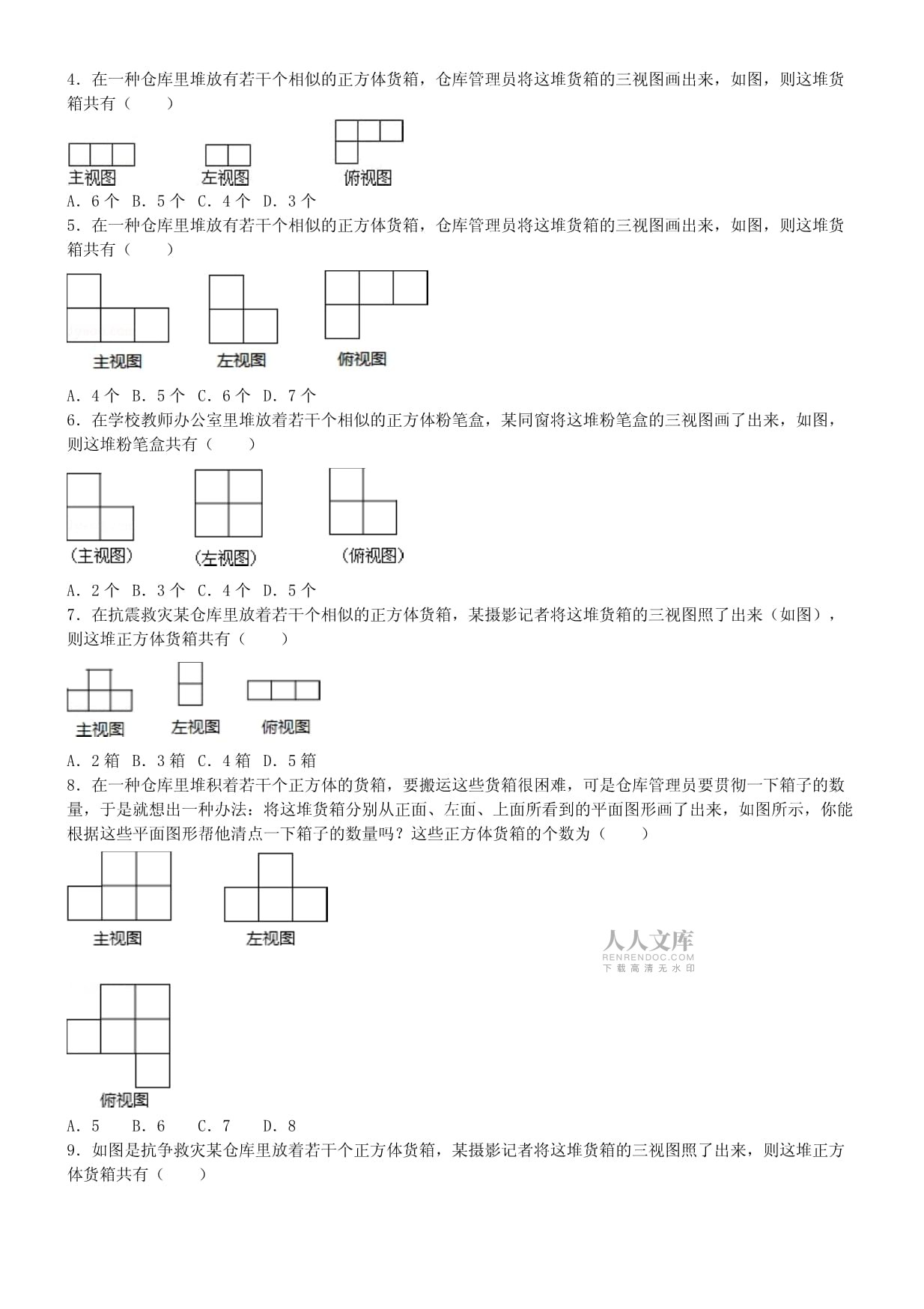
D．12箱分析：由三视图可知，这堆货箱共有从前到后3行，从左到右3列。由左视图：第一行均为1层，第二行最高2层，第三行最高3层；由主视图：第一列、第三列均为1层，第二列（中间列）最高为3层。故第二行、第二列为2层，第三行第二列为3层，其它皆为1层。各行、各列小正方体的个数如俯视图中所示。这堆货箱共有3+1+1+2+1+1=9（箱）。练习题1．在一仓库里堆放着若干个相似的正方体货箱，仓库管理员将这堆货箱的三视图画了出来（如图），则这堆正方体货箱共有（）A．4箱 B．5箱 C．6箱 D．7箱2．在仓库里堆放着若干个相似的正方体货箱，仓库管理员将这堆货箱从三个方向看到的图形画了出来，如图所示，则这堆正方体货箱共有（）A．9箱 B．10箱 C．11箱 D．12箱3．在某仓库里堆放着若干个相似的正方体货箱，管理员将这堆货箱的三视图画了出来（如图），则这堆正方体货箱共有（）A．8箱 B．9箱 C．10箱 D．11箱4．在一种仓库里堆放有若干个相似的正方体货箱，仓库管理员将这堆货箱的三视图画出来，如图，则这堆货箱共有（）A．6个 B．5个 C．4个 D．3个5．在一种仓库里堆放有若干个相似的正方体货箱，仓库管理员将这堆货箱的三视图画出来，如图，则这堆货箱共有（）A．4个 B．5个 C．6个 D．7个6．在学校教师办公室里堆放着若干个相似的正方体粉笔盒，某同窗将这堆粉笔盒的三视图画了出来，如图，则这堆粉笔盒共有（）A．2个 B．3个 C．4个 D．5个7．在抗震救灾某仓库里放着若干个相似的正方体货箱，某摄影记者将这堆货箱的三视图照了出来（如图），则这堆正方体货箱共有（）A．2箱 B．3箱 C．4箱 D．5箱8．在一种仓库里堆积着若干个正方体的货箱，要搬运这些货箱很困难，可是仓库管理员要贯彻一下箱子的数量，于是就想出一种办法：将这堆货箱分别从正面、左面、上面所看到的平面图形画了出来，如图所示，你能根据这些平面图形帮他清点一下箱子的数量吗？这些正方体货箱的个数为（）A．5 B．6 C．7 D．89．如图是抗争救灾某仓库里放着若干个正方体货箱，某摄影记者将这堆货箱的三视图照了出来，则这堆正方体货箱共有（）A．5箱 B．6箱 C．7箱 D．8箱10．在学校仓库里堆放着若干个盒相似的正方体小粉笔盒，仓库管理员将这堆粉笔盒的三视图画了出来，如图所示，则这堆正方体小粉笔盒共有（）A．11盒 B．10盒 C．9盒 D．8盒11．在一种仓库里堆积着正方体的货箱若干，要搬运这些箱子很困难，可是仓库管理员要贯彻一下箱子的数量，于是就想出一种方法：将这堆货品的三种视图画了出来，如图，你能根据三视图，帮他清点一下箱子的数量吗？这些正方体箱的个数是（）A．6 B．7 C．8 D．912．在一种仓库里堆积着正方体的货箱若干，要搬运这些箱子很困难，可是仓库管理员要贯彻一下箱子的数量，于是就想出一种方法：将这堆货品的三种视图画了出来，如图，你能根据三视图，帮他清点一下箱子的数量吗？这些箱子的个数是（）A．9 B．8 C．7 D．613．仓库里堆积着正方体的货箱若干，根据如图所示的三视图可得出箱子的个数是（）A．6 B．7 C．8 D．9二、根据两种视图拟定计数范畴（成果不唯一的计数）（1）懂得几何体的主视图和俯视图

例2.如图2，是由若干个（不不大于8个）大小相似的正方体构成的一种几何体的主视图和俯视图，则这个几何体的左视图不可能是（

）。分析：由给出的主视图、俯视图能够看出，该几何体共有2行，3列。第1列均为1层，第2列最高2层，第3列最高3层。左视图为A时，第1行、第2行最高均为3层。几何体中，第1列第1行为1层；第2列第1行、第2行均可为1层或2层，，但不能同时为1层；第3列两行均为3层。此时，小正方体的个数如俯视图A所示，最少为1+2+1+3+3=10（个），最多为1+2+2+3+3=11个。

左视图为B时，第一行均为1层，第二行最高为3层。几何体中，第1列第1行为1层；第2列第1行为1层，第2行均可为2层；第3列第1行为1层，第2行为3层。此时，小正方体的个数如俯视图B所示。小正方体个数为1+1+1+2+3=8（个）。左视图为C时，第1行最高为2层，第2行最高为3层。几何体中，第1列第1行为1层；第2列第1行为1层或2层，第2行均为1层或2层，但不能同时为1层；第3列第1行为1层或2层（不能与第2列第1行同时都为1层），第2行为3层。此时，小正方体的个数如俯视图C所示。小正方体最少为1+2+1+1+3=8（个），最多为1+2+2+2+3=10个。左视图为D时，第1行最高为3层，第2行最高为2层。几何体中，第1列第1行为1层；第2列第1行为1层或2层，第2行均为1层或2层，但不能同时为1层；第3列第1行为3层，第2行为1层或2层（不能与第2列第2行同时为1层）。此时，小正方体的个数如俯视图C所示。小正方体最少为1+1+3+2+1=8（个），最多为1+2+2+2+3=10个。练习题1．如图是一种由若干个相似的小正方体构成的几何体的主视图和俯视图，则能构成这个几何体的小正方体的个数最多是（）A．11个 B．12个 C．13个 D．14个2．如图是一种由若干个相似的小正方体构成的几何体的主视图和俯视图，则能构成这个几何体的小正方体的个数最多是（）A．11个 B．12个 C．13个 D．14个3．由若干个相似的小正方体搭成的一种几何体的主视图和俯视图如图所示，则构成这个几何体的小正方体的个数最多有（）A．4 B．5 C．6 D．74．如图，分别是由若干个完全相似的小正方体构成的一种几何体的主视图和俯视图，则构成这个几何体的小正方体的个数最多为（）A．7个 B．8个 C．9个 D．10个5．由n个相似的小正方体堆成的几何体，其主视图、俯视图如图所示，则n的最大值是（）A．16 B．18 C．19 D．206．如图，由几个相似的小正方体搭成的几何体的主视图和俯视图，构成这个几何体的小正方体的个数最多是（）A．7个 B．8个 C．9个 D．10个7．由若干个相似小正方体组合成一种几何体，使组合几何体的主视图、俯视图如图所示．这样的组合几何体不只有一种，它的构成最少需要x个小正方体，最多需要y个小正方体．则y﹣x的值为（）A．4 B．3 C．2 D．18．一种几何体由某些大小相似的小正方体构成，如图是它的主视图和俯视图，那么构成该几何体所需小正方体的个数最少为（）A．3 B．4 C．5 D．610．一种几何体由某些大小相似的小正方体构成，如图是它的主视图和俯视图，那么构成该几何体所需小正方体的个数最少为（）A．4 B．5 C．6 D．711．某几何体由某些大小相似的小正方体构成，如图分别是它的主视图和俯视图，那么要构成该几何体，最少需要多少个这样的小正方体（）A．3 B．4 C．5 D．616．如图是一种由小正方体构成的物体的主视图和俯视图，由这两个图能够拟定此物体所需的小正方形最少为（）A．7个 B．8个 C．10个 D．12个17．由某些大小相似的小正方体搭成的几何体的主视图与俯视图如图所示，则搭成这个几何体的小正方体的个数最多为（）A．3个 B．4个 C．5个 D．不能拟定18．如图是某些大小相似的小正方体构成的几何体的主视图和俯视图，则构成这个几何体的小正方体最多块数是（）A．8 B．10 C．12 D．1419．如图是由某些大小相似的小正方体构成的几何体的主视图和俯视图，则构成这个几何体的小正方体的块数最多是（）A．5 B．6 C．7 D．820．如图，是由某些大小相似的小正方体构成的几何体的主视图和俯视图，则构成这个几何体的小正方体最多块数是（）A．9 B．10 C．11 D．1219．如图是由某些相似的小正方体构成的几何体的主视图和左视图，在这个几何体中，小正方体的个数可能是个．20.桌上摆着一种由若干个相似正方体构成的几何体，其主视图和左视图如图所示，这个几何体最多能够由个这样的正方体构成．21．如图，一种几何体是由某些大小相似的小正方体摆成的，其主视图与左视图如图所示，则构成这个几何体的小正方形最少有个，最多有个．22．一种几何体是由若干个相似的正方体构成的，其主视图和左视图如图所示，则这个几何体最多可由个这样的正方体构成．23．如图，一种几何体的主视图和左视图相似．则摆成这个几何体最少需要个小正方体．25．一种几何体是由某些大小相似的小正方体摆成的，其主视图与左视图如图所示，则构成这个几何体的小正方体最少有个．26．某一物体由若干相似的小正方体构成，其主视图，左视图分别如图，则该物体所含小正方体的个数最多有个．27．桌上摆着一种由若干个相似正方体构成的几何体，其主视图和左视图如图所示，因此这个几何体最多能够由个这样的正方体构成．29．由某些大小相似的小正方体构成的简朴几何体的主视图和左视图如图所示．（1）请你画出这个简朴几何体三种不同的俯视图；（2）若构成这个简朴几何体的小正方体的块数为n，请你写出n的全部可能值．30．桌子上摆放着一种由若干个相似小正方体构成的几何体，其主视图和左视图如图所示，试画出它的俯视图．（3）懂得几何体的俯视图和左视图1．用某些大小相似的小正方体构成的几何体的左视图和俯视图如图所示，则构成这个几何体的小正方体的块数，最多可能是（）A．17 B．18 C．19 D．202．由某些大小相似的小正方体搭成的几何体的左视图和俯视图，如图所示，则搭成该几何体的小正方体的个数最少是（）A．4 B．5 C．6 D．73．如图，由某些完全相似的小正方体搭成的几何体的俯视图和左视图，构成这个几何体的小正方体的个数是（）A．5或6或7 B．6或7 C．6或7或8 D．7或8或91.如图是一种长方体纸盒的展开图，求这个纸盒的表面积和容积．（纸的厚度不计）（单位：厘米）2.如图所示是一种长方体纸盒的展开图．（单位：cm）

（1）做这个铁盒需要多少铁皮？

（2）这个铁盒的容积是多少毫升？（铁皮厚度无视不计）3.右图是一种长方体纸盒的展开图。如果不要盖子，做这个纸盒需要多少材料？4.看图计算，如图是长方体纸箱的展开图，请你根据有关数据，求出纸箱的体积．（单位：分米）找次品3瓶木糖醇，其中一瓶少了2粒，你能找出少的那一瓶吗？ 在天平的左右两边各放1瓶钙片如果平衡，次品是剩余的那瓶 5瓶木糖醇，其中一瓶少了2粒，最少称几次就能确保把次品找出来？应当如何称？在9个零件里有1个是次品(次品重某些)，用天平称，最少称几次就一定能找出次品来?“找次品”三字诀：找次品，办法多；3而均，最适宜；无法均，相差1；请切记，找得易3个零件里面找次品最少称几次确保找到次品？9个零件里面找次品最少称几次确保找到次品？27个零件里面找次品最少称几次确保找到次品？81个零件里面找次品最少称几次确保找到次品？要分辨的物品数目确保能找出次品需要测的次数2～34～910～2728～8182

～243……12345……《找次品》练习题一、填空。（10分）1、有5颗外观同样的玻璃球，其中4颗同样重，另外一颗轻某些，如果用天平称（）次能确保称出来，最少（）次有可能称出来。2、有10瓶药，其中一瓶少2粒，最少称（）次确保能称出来。3、有3包饼干，其中两袋质量相似，另一包不知是重还是轻，用天平称（）次，确保能找到这包饼干。4、有5包糖果，用天平找出质量局限性的一包，最少需要称（）次。5、有15瓶水，14瓶是纯净水，另外一瓶是盐水，用天平最少称（）次，确保能找到这瓶盐水。二、解决问题。（40分）1、有4袋奶粉，其中一袋质量轻某些，最少用天平称几次才干把它找出来？说说过程。2、有12盒糖果，其中有11盒质量相似，另一盒少3块，如果用天平称，最少称多少次能确保找出这盒糖果？3、有7瓶钙片，其中有一瓶少了5片，你用天平最少称几次能确保找出它？4、有25枚钻戒，其中一枚重量不够，用天平最少称几次能确保找出这枚钻戒