2021-2022学年北师大版八年级数学下册第一章三角形的证明同步练习练习题（含详解）

北师大版八年级数学下册第一章三角形的证明同步练习

考试时间：90分钟；命题人：数学教研组

考生注意：

1、本卷分第I卷（选择题）和第II卷（非选择题）两部分，满分100分，考试时间90分钟

2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上

3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新

的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I卷（选择题30分）

一、单选题（10小题，每小题3分，共计30分）

1、如图，已知放△力台。中，Z<7=90°,/力=30°,在直线6c上取一点儿使得△为6是等腰三角

形，则符合条件的点。有（）

A.1个B.2个C.3个D.4个

2、下列各组数中，能构成直角三角形的是（）

A.4,5,6B.1,b-JlC.6,8,13D.5,12,15

3,如图，在△/阿中，NU90°,点〃为比1上一点，DELAB^E,并且应厂为〃1上一点,

则下列结论中正确的是（）

A.DE=DFB.BD=FDC.Z1=Z2D.AB=AC

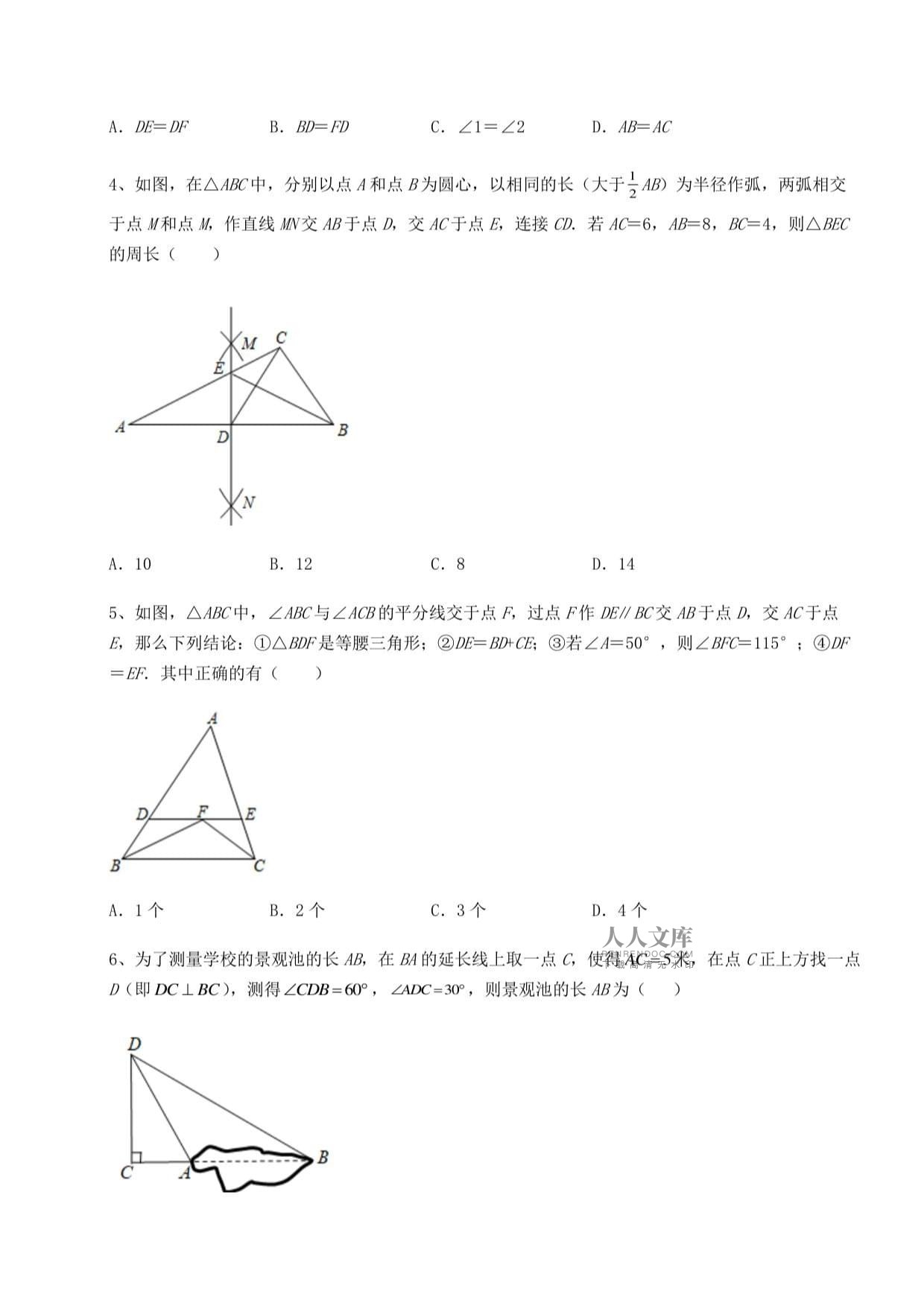
4、如图，在中，分别以点4和点8为圆心，以相同的长（大于g48）为半径作弧，两弧相交

于点”和点乱作直线网,交力8于点〃，交然于点£,连接S若〃=6,麴=8,及7=4,则△庞。

的周长（）

A.10B.12C.8D.14

5、如图，△0式中，N4a'与N43的平分线交于点凡过点尸作应〃回交四于点〃交然于点

E,那么下列结论：①△即是等腰三角形；②DE=BACE；③若N4=50°,则/郎T=115°；@DF

=EF.其中正确的有（）

A.1个B.2个C.3个D.4个

6、为了测量学校的景观池的长48,在刃的延长线上取一点G使得AC=5米，在点C正上方找一点

〃（即DCL3C）,测得/CO3=60。，Z4ZX?=30°,则景观池的长48为（）

A.5米B.6米C.8米D.10米

7、如图，等题直角4中，OA^OB,过点4作A£），OA,若线段上一点。满足

NCDB=NOBD,则NCB。的度数为（）

A.42°B.43°C.45°D.60°

8、如图：将一张长为40cm的长方形纸条按如图所示折叠，若AB=3BC,则纸条的宽为（）

9、等腰三角形的一个角是80°,则它的一个底角的度数是（）

A.50°B.80°C.50°或80°D.100°或80°

10、如图，在小中，AB^AC,ZA=120。，BC=6cm,A8的垂直平分线交BC于点M,交

A8于点E,AC的垂直平分线交于点N,交AC于点尸，则的长为（）

A.4cmB.3cmC.2cmD.1cm

第n卷（非选择题70分）

二、填空题（5小题，每小题4分，共计20分）

1,如图，在四边形48应中，NB=NA,/f=90°,点。在4?上，40：80=5：11,连接切，若点

〃在位的垂直平分线上且满足N4=2N川C,。=10,则线段的长为_____.

2、在4中，ZBAC=90°,ZC=30°.用无刻度的直尺和圆规在8c边上找一点〃，使小。。为

等腰三角形.下列作法正确的有________个.

3、同学们，我们在今后的学习中会学到这个定理：在直角三角形中，如果一个锐角等于30。，那么

它所对的直角边等于斜边的一半.即：如图，在中，N4第=90°,若N48C=30°,则

AC=；A8.问题：在RtAABC,/48=90°,NABC=30°,AC=6，点〃是边比■的中点，点£

是斜边4?上的动点，连接加把△成£沿直线应折叠，点6的对应点为点£当直线4U/6时，

/£的长为.

4、如图，在△力比'中，点。在的延长线上，NG46平分线与⑦的垂直平分线交于点E,连接

BE.若NACB=28°,N⑸%=25°,则N硼的度数为____°.

c

5,如图,在4中，AC的垂直平分线交AC于点E,交BC于点、D,△ABD的周长为13cm,

AE=4.5cm,则4的周长cm.

三、解答题（5小题，每小题10分，共计50分）

1、已知：在中，AD平分NBAC,AE=AC.求证：AD//CE.

2、已知，在况'中，N刃C=30°,点。在射线■上，连接NOga,点。关于直线〃'的

对称点为笈点后关于直线4?的对称点为a直线周'分别交直线4G四于点机N,连接〃；AE,

CE.

（1）如图1,点〃在线段比1上.

①根据题意补全图1；

②4AEF=（用含有。的代数式表示），ZAMF=°；

③用等式表示线段物，，场.，妒之间的数量关系，并证明.

(2)点〃在线段8c的延长线上，且/力〃<60°,直接用等式表示线段协，皿；，妒之间的数量关

系，不证明.

3、如图，长方形力。仇?在直角坐标系中，点/在y轴上，点6在x轴上，已知点C的坐标是(8,

4).

(1)求对角线4?所在直线的函数关系式；

(2)对角线48的垂直平分线腑交x轴于点M,连接AM,求线段4〃的长；

(3)若点尸是直线46上的一个动点，当△必〃的面积与长方形力"的面积相等时，求点尸的坐

标.

4、如图，是小的角平分线，1于点

BD

(1)用尺规完成以下基本作图：过点作1于点，连接交于点.(不写作

法，保留作图痕迹)

(2)在(1)中所作的图形中，求证：1

5、在△月况'中，AACB=W.现给出以下3个关系：①①垂直于力6,②龙平分/四C,③4CFE=

ACEF,请你从中任选两个作为条件，另一个作为结论构成一个命题，并证明该命题的正确性.

-参考答案-

一、单选题

1、B

【分析】

根据等腰三角形的判定定理，结合图形即可得到结论.

【详解】

解：以点从8为圆心，力8长为半径画弧，交直线比于两个点耳,鸟，然后作48的垂直平分线交直线

比于点鸟，如图所示:

1

BC2

•：ZC=90°，ZJ=30°，

：.ZABC=60°,

•••AP3=BP',

：.△ABA是等边三角形，

二点&2重合，

...符合条件的点。有2个；

故选B.

【点睛】

本题主要考查等腰三角形的性质及等边三角形的性质与判定，熟练掌握等腰三角形的性质是解题的关

键.

2、B

【分析】

欲求证是否为直角三角形，这里给出三边的长，只要验证两小边的平方和等于最长边的平方即可.

【详解】

解：A、52+4V62,不能构成直角三角形，故不符合题意；

B,12+12=（血）2,能构成直角三角形，故符合题意；

C、62+8V132,不能构成直角三角形，故不符合题意；

D>122+5V152,不能构成直角三角形，故不符合题意.

故选:B.

【点睛】

本题考查勾股定理的逆定理的应用，正确应用勾股定理的逆定理是解题的关键.

3、C

【分析】

在直角三角形叱中，利用斜边长度大于直角边长度，可以得到班>/r,又所以DF>DE,

故A选项错误，同理，D选项错误，假设劭=能则可以判定△瞅丝△力?，，所以NB=NDFC,而在

题目中，/B是定角，/%'C随着尸的变化而变化，假设不成立，故6选项是错误的，由DE=DC,

DCVAC,DELAB,根据Rt△的gRtaZO(HL)得到C选项是正确的.

【详解】

解：(1)在直角三角形式尸中，利用斜边长度大于直角边长度，可以得到外>/匕又DC=DE,所以

DF>DE,

故A选项错误；

(2)4BDE与ADCF,只满足N颇=//尸=90°,&7=龙的条件，不能判定两个三角形全等，故不

能得到BD=FD,

另一方面，假设蚪如，

在RtADBE与/\DFC中,

\BD=FD

\DE=DCJ

：.Rt/\DBE^Rt/\DFC(应)，

NB=ADFC,

而图中N6大小是固定的，/加'C的大小随着尸的变化而变化，故上述假设是不成立的，

故B选项错误；

(3)SAC,DELAB,DC=DE,

在Rt△曲和Rt△〃勿中，

[AD=AD

\DE=DC'

...RtZ\ZK4gRt△〃0(HL),

.-.Z1=Z2,

故c选项正确；

(4)在直角三角形4%中，利用斜边长度大于直角边长度，可以得到4Q4C,

故D选项错误，

故选：C.

【点睛】

本题考查了全等三角形的性质与判定，三角形三边不等关系关系，掌握全等三角形的性质与判定，直

角三角形三边关系是解题关键.

4,A

【分析】

由垂直平分线的性质得=故△BEC的周长为BE+EC+BC=AC+BC,计算即可得出答案.

【详解】

由题可知：MN为的垂直平分线，

AE=BE,

,/AC=6,

,\AC=AE+EC=BE+EC=6,

••CRM=BE+EC+BC=6+4=10.

故选：A.

【点睛】

本题考查垂直平分线的性质，掌握垂直平分线上的点到线段两端的距离相等是解题的关键.

5、C

【分析】

根据平行线的性质和角平分线的定义以及等腰三角形的判定和性质逐个判定即可解答.

【详解】

解：•.•即是N48的角平分线，

：.ADBF=ACBF,

'：DE//BC,

:.乙DFB=4CBF,

：.ADBF=ADFB,

：.BD=DF,

△烧火是等腰三角形；故①正确；

同理，EF=CE,

：.DE=DF+EF=BD^CE,故②正确；

：//=50°,

：.ZABOZACB^130°,

■:BF平令NABC,CF平■分乙ACB,

：.NFBC=-ZABC/FCB=-ZACB,

22

:.NFBC+4FCB=W(ZABOZACB)=65°,

：.ZBFC=180°-65°=115°,故③正确；

当△/阿为等腰三角形时，DF=EF,

但△?!阿不一定是等腰三角形，

:.DF不一定等于EF,故④错误.

故选：C.

【点睛】

本题主要考查等腰三角形的性质、角平分线的定义及平行线的性质等知识点，根据两直线平行、内错

角相等以及等角对等边来判定等腰三角形是解答本题的关键.

6、D

【分析】

利用勾股定理求出切的长，进而求出比1的长，AB=BC-AC即可求解.

【详解】

解：VDC±BC,

：./DCS=90°,

VZ4£X7=30°,AC=5,

AAD=2AC=]0,

•*-CD=yjADr-AC2=5A/3，

NCOS=60。，

，NB=30。，

二8。=2c£>=10后，

BC^^BCr-CD1=15，

AAB=BC-AC=15-5=10m,

故选：D.

【点睛】

本题考查勾股定理的应用，解题关键是掌握勾股定理.

7、C

【分析】

过点B作3E_L4),交AO的延长线于E,BFLCD于F,由“A45”可证ABE£>=AB田，可得

BE=BF=BO,ZEBD=/FBD,由"HZ/'可证RtBCF冬RtRCO,可得NOBC=NCBF,即可求解.

【详解】

解：如图，过点B作8£_L4),交4)的延长线于E,BFLCD于F,

-.-AD±AO,BDVAO,

;.ADHBO,

:.ZEDB=NDBO,

又•；NCDB=NOBD,

:.^EDB=ZBDC,

440=45。，DAVAO,

ZDAB=ZBAO=45°,

又•.•BELAD,BOA.AO,

BE—BOf

在ABED和岫FD中，

NE=NBFD=90。

<4BDE=Z.BDF,

BD=BD

/.ABED^ABFD(AAS),

，BE=BF=BO,NEBD=NFBD,

在和R14BCO中,

[BF=BO

[BC=BCf

：.RUBCF沿Rt巫CO,

:.NOBC=NCBF,

ZE+ZE4O+ZAOB+ZOBE=360°,

NOBE=90。，

ZEBD+NDBF+/FBC+NCBO=9QP,

.*.ZDBC=45°,

故选：c.

【点睛】

本题考查了全等三角形的判定和性质，等腰直角三角形的性质，角平分线的性质等知识，添加恰当辅

助线构造全等三角形是本题的关键.

8、B

【分析】

如图，延长M7交力〃的延长线于点R设小x,则力生3筋利用折叠的性质和等腰直角三角形的性质

可表示出纸条的宽物0,的长，从而可表示出纸条的长2/W的长，然后根据长方形纸条的长为40,

可得到关于x的方程，解方程求出x的值，即可求出纸条的宽.

【详解】

解：如图，延长A0交力〃的延长线于点R

设BOx,则AB^Zx,

•••折叠，

:.AB=BM=C0=CD=P0=3x,

...纸条的宽为：物=A。3A"+3产户7x,

二纸条的长为：2PN=2（7肝3x）=20年40

解得：产2,

...纸条的宽A37X2=14.

故答案为：B.

【点睛】

此题考查了折叠的性质，等腰直角三角形的性质，一元一次方程应用题，解题的关键是正确分析题目

中的等量关系列出方程求解.

9、C

【分析】

已知给出一个角的的度数为80。，没有明确是顶角还是底角，要分类讨论，联合内角和求出底角即

可.

【详解】

解：等腰三角形的一个角是80°,

当80°为底角时，它的一个底角是80°,

1Qno_onoinno

当80。为顶角时，它的一个底角是；=券=50。,

则它的一个底角是50°或80°.

故选：C.

【点睛】

本题考查等腰三角形的性质，内角和定理，掌握分类讨论的思想是解决问题的关键.

10、C

【分析】

此类题要通过作辅助线来沟通各角之间的关系，首先求出△8%与△。必是等腰三角形，再证明△，碗V

为等边三角形即可.

【详解】

解：连接掰AN,

的垂直平分线交回于秋交AB于E,4C的垂直平分线交比于小交4c于E

CN=AN,

:.NMAB=NB,NCAgNC,

砌C=120°,AB=AC,

.♦.N6=/C=30°,

：.ABAM+ACAN=^°,N4网占N—60°,

△川邠是等边三角形，

：.AM=AN=MN,

：.BM=MN=NC,

■:BC=6cm,

:・MN=2cm.

故答案为2cm.

故选：C.

【点睛】

本题考查的知识点为线段的垂直平分线性质以及等腰三角形的性质；正确作出辅助线是解答本题的关

键.

二、填空题

-7

【分析】

根据题意过点〃作％CFX.AB,连接然、DE,先证明△以庐△救和△山吐△*C,进而设

AABC=5x,AB=BD=nx,Af^y,则止16尸y,通过勾股定理建立方程求解即可.

【详解】

解：过点。作，GJ.比，CFLAB,连接丝、DE,

点。在四的垂直平分线上，DGLEC,

：.DE=DC,ZEDG=ZCDG,

VZJ£r=90°,DGX.EC,NEAD=2/BDC,

：.AE//DG,NEAD=NGDF=2NBDC,ZAED=NGDE,

ZBDC=ZCDG=ZEDG=ZAED,

,:NB=NEAD,ZBDC=ZAED,DE=DC,

:.△ADE^XBCD,AE=BD,

■:DGLEC,CFLAB,ZBDC=NCDG,CD-CD,

:.XGDC^XFDC,

又：宓=10,CG^CE,

小份5,

"：AD\BD=5：11,

设AABO5x,AE=BAlAx,AQy,则止16『y,

由勾股定理片+第=<^+力尸得至lj121^+100=25+/①

由勾股定理得初=小+欧得至lj25V=25+(16x-y)2②

联立①②可解得x=

4

80=11x2=生.

44

故答案为：斗.

4

【点睛】

本题考查全等三角形的判定与性质以及勾股定理的应用和垂直平分线性质，熟练掌握通过垂直平分线

性质和角平分线性质构造全等三角形是解题的关键.

2、3

【分析】

根据图中的圆心、半径已经角平分线、垂直平分线的作法，依次判断即可得.

【详解】

解：第一个图以，为圆心，4C长为半径，

...△ACD为等腰三角形，符合题意；

第二个图为作N8AC的角平分线，无法得到△ACO为等腰三角形，不符合题意；

第三个图以6为圆心，力6长为半径，

...为等腰三角形，

,:ZC=30°,

4=60。，

二△M£>为等边三角形，

,ZBA£>=60°,

,ZZMC=90°-60°=30°,

AC=ADAC,

：.CD=DA,

...△ACD为等腰三角形，符合题意；

第四个图为作线段4C的垂直平分线，可得/M=DC,

.♦.△AC。为等腰三角形，符合题意；

综上可得：有三个图使得zMCD为等腰三角形，

故答案为：3.

【点睛】

题目主要考查等腰三角形的性质及角平分线、垂直平分线的作法，熟练掌握各个图形的作法是解题关

键.

3,也或

2

【分析】

如图1所示，设ZF与46交点为G,先求出AB=2G，BC=3,由。是6c的中点，可以得到

1313

BD=-BC=^-由折叠的性质可知N片N左30。，B&EF,即可得到。6=-8。=二，

22f24

EG=\EF=\BE,BG=』B»-DG,=强,由此即可求出丝的长；如图2所示，同理可得

224

OG=280=[,BGZBD-DG。=也，EGJEF=!BE,则BE=8G+GE=』8G=M,

AE=AB-BE=—^~

8

【详解】

解：如图1所示，设DF与46交点为G,

：/月吐30°,ZACB=90°,

，AB=2AC=2G,

BC=y/AB2-AC2^3>

•"是比的中点，

BD=-BC=~,

22

图1

由折叠的性质可知N4N比30°,B俣EF,

■:DFLAB,

"DGK/FGB邳）。,

1311

ADG=-BD=-,EG=-EF=-BE,

2422

BG=y/BD2-DG2=—，

4

.R口_2

••DE=—IJCJ=—,

32

AE=AB-BE=^-

如图2所示，延长/力与A?交于点G,

同理可求出。=斗,EG=2*

二BE=BG+GE=2BG=—

2

二AE=AB-BE=—,

2

故答案为：空或显.

22

【点睛】

本题主要考查了含30度角的直角三角形的性质，勾股定理，旋转的性质，熟练掌握含30度角的直角

三角形的性质是解题的关键.

4、53

【分析】

过点£作£匕“；ENLAD,垂足分别为机N,证明应△比侬应△即Y进而可得结果.

【详解】

解答：解：如图，过点£作也工/C,EN1AD,垂足分别为例N,连接

•.F£是平分线，

：.EM=EN,

•••£1是"的垂直平分线上的点，

：.EC=EB,

：.ZECB=』EBC=25°,

在以和RtAEBN中,

[EC=EB

[EM=EN'

二RtXEC胫RtAEBNqHD,

：.4EBN=NECM=4ACB^NECB=2&+25°=53°.

故答案为：53.

【点睛】

本题考查的是线段垂直平分线的判定、等腰三角形的性质以及三角形内角和定理，掌握到线段的两个

端点的距离相等的点在垂直平分线上是解题的关键.

5、22

【分析】

根据“AC的垂直平分线交AC于E,交BC于3"可知"'是4c的垂直平分线，利用中垂线的性质可

得屐加，由△回£）的周长为4/舰13cm,可知AB+BC=12,再求404^办4.5+4.5=9cm,从而

可以得到△/a'的周长.

【详解】

解：应是4C的垂直平分线，

:.DA=DC,AE^CB^X.5cm

C.AC=AE+CE=^.5+4.5=9cm,

的周长为A/B必盼A/B讣DC=A拼BC=13cm,

...△4%的周长为：力加卧4>13+9=22cm.

故答案为22.

【点睛】

本题考查的是线段垂直平分线的性质，知道线段垂直平分线上的点到线段两端的距离相等，将△48〃

的周长转化为4a比是解题的关键.

三、解答题

1、见解析.

【分析】

先根据角平分线的定义得到/创场3NBAC,再根据等腰三角形的性质和三角形外角定理得到N后g

ABAC,从而得到N为/即可证明4〃〃出

【详解】

解：平分/力。

，NBAD=gABAC,

■:A芹AC,

：.NE=NACE,

,：NE+NAC氏/BAC,

：.N斤3NBAC,

：.NBAD=NE,

：.AD//CE.

【点睛】

本题考查了角平分线的定义，等腰三角形的性质，平行线的判定，三角形外角定理，熟知相关定理并

灵活应用是解题关键.

2、(1)①见解析；②60。-。，60；@MF=MA-\-ME,证明见解析；(2)MF=MA-ME

【分析】

(1)①按照要求旋转作图即可；②由旋转和等腰三角形性质解出//能再由三角形外角定理求出

NAMF；③在座上截取6F=,四，连接/G,证明△力用经△/图/且为等边三角形后即可证得,如

=MA+ME；

(2)根据题意画出图形，根据含30°的直角三角形的性质，即可得到结论.

【详解】

解：(1)①补全图形如下图:

A

②•：4CA序乙DAOa,

・・・N胡尼300+a

：.ZFA^2X（30°+。）

."4231=60。-a；

2

VAAM^ACAE+AAEF-a+60°-a=60°,

故答案是：60°-a,60。；

③MF=MA+ME.

证明：在此上截取距一监；连接力G.

A

BD

•.•点〃关于直线4c的对称点为E,

：./\ADC^/\AEC.

：.ZCAE=/CAD=a.

,：ZBAC=30°,

.•.N£4A'=3O°+«.

又•.•点K关于直线46的对称点为F,

.♦./6垂直平分EF.

：.AF=AE,AFAN=AEAN=30°+«,

..„,180°-2(300+a)

..ZF=ZAEF=-------i---------L=60°-a

2

N4MG=60°-ar+a=60°.

,.,AF=AE,NF=NAEF,GF=ME,

：./\AFG9丛AEM.

：.AG=AM.

又盼=60°,

...△4GV为等边三角形.

：.MA=MG.

：.MF=MG+GF=MA+ME.

(2)MF=MA-ME,理由如下：

如图1所示，

•••点£与点少关于直线48对称，

.../4彼90°,NE=NF,

又：NA%,沪30°,

：.AM=2MN,

・・・4沪2人妣2£犷=gME,

:・M户AM-ME；

如图2所示，

•・,点E与点、尸关于直线四对称，

AZAA^90°,N4NF,

:/胡沪30°,

・・・4沪2A胴

JA忙2MF+2N六2MRNE+帕M吩MF,

:.M六MA—ME；

A

综上所述：，汜物-您

【点睛】

本题考查轴对称、三角形全等判定与性质、等边三角形判定与性质，掌握这些是本题关键.

3、(1)y=~1x+4；(2)5；(3)点尸的坐标为1(0R号,-yJ.4)或(一詈192，yQJ.)

【分析】

(1)由坐标系中点的意义结合图形可得出46点的坐标，设出对角线4?所在直线的函数关系式，

由待定系数法即可求得结论；

(2)由勾股定理求出力6的长，再结合线段垂直平分线的性质，可得4Q8区OM=OB-BM,再次利用

勾股定理得出4"的长；

(3)(方法一)先求出直线力［的解析式，设出产点坐标，由点到直线的距离求出力/边上的高A,再

结合三角形面积公式与长方形面积公式即可求出夕点坐标；

(方法二)由△为"的面积与长方形3面的面积相等可得出义用"的值，设点P的坐标为(x,—x+

4),分点。在4"的右侧及左侧两种情况，找出关于x的一元一次方程，解之即可得出点。的坐标，

此题得解.

【详解】

解：（1）♦.•四边形力施'为长方形，且点C的坐标是（8,4）,

：.AO=CB^\,0B=AC=8,

.•/点坐标为（0,4）,3点坐标为（8,0）.

设对角线力6所在直线的函数关系式为y=kx+b,

1"4=6k=――

则有cQ,小解得：2,

[0=8%+6b=4

二对角线46所在直线的函数关系式为y=-1x+4.

（2）VZAOB=90°,

；•勾股定理得：AB=^AO2+OB2=475,

;即垂直平分AB,

:.BN=AN=WAB=2逐.

•，即为线段的垂直平分线，

：.AM=BM

设4仁a,贝8仁a,OM=8—a,

由勾股定理得，a=42+（8—a）2,

解得a=5,即/#=5.

（3）（方法一）：。仁3,

.•.点〃坐标为（3,0）.

又•.•点1坐标为（0,4）,

4

直线417的解析式为尸一§x+4.

•・,点P在直线力及y=—gx+4上,

，设一点坐标为（/，-^w+4）,

2-4

4_32

点尸到直线AM：-x+y-4=0的距离h=

△/W的面积SN产"M•H::屈=s〃L=32,

解得加=±*，

向上。的加『平，J284412884.

故点户的坐标为（―-――）或（----1—）.

阴

（方法一.）./S长方形0黄方=8X4=32,

S^/>A.V=32・

设点尸的坐标为（X,—Jx+4）.

当点尸在加右侧时，五小产"孙（为一力）=yX5X（4+yx-4）=32,

山口128

解得：x~~

12844

・••点P的