一元一次不等式与一元一次不等式组中考复习课

明确：2019年中考数学考纲要求不等式和不等式组知识要点知识技能目标了解理解掌握运用不等式的意义√

不等式的基本性质

√

解简单的一元一次不等式

√

解由两个一元一次不等式组成的不等式组

√

根据具体问题中的数量关系列一元一次不等式（组）

√

不等式与方程及函数的内在联系

√

运用一次函数与一元一次不等式解决实际问题

√考点一：一元一次不等式的意义及基本性质1．不等式用

连接起来的式子叫做

．常见的不等号有五种：2.不等式的基本性质

(1)不等式的两边都加上(或减去)同一个

，不等号的方向

．

(2)不等式的两边都乘以(或除以)同一个

，不等号的方向

．（3)不等式的两边都乘以(或除以)同一个

，不等号的方向

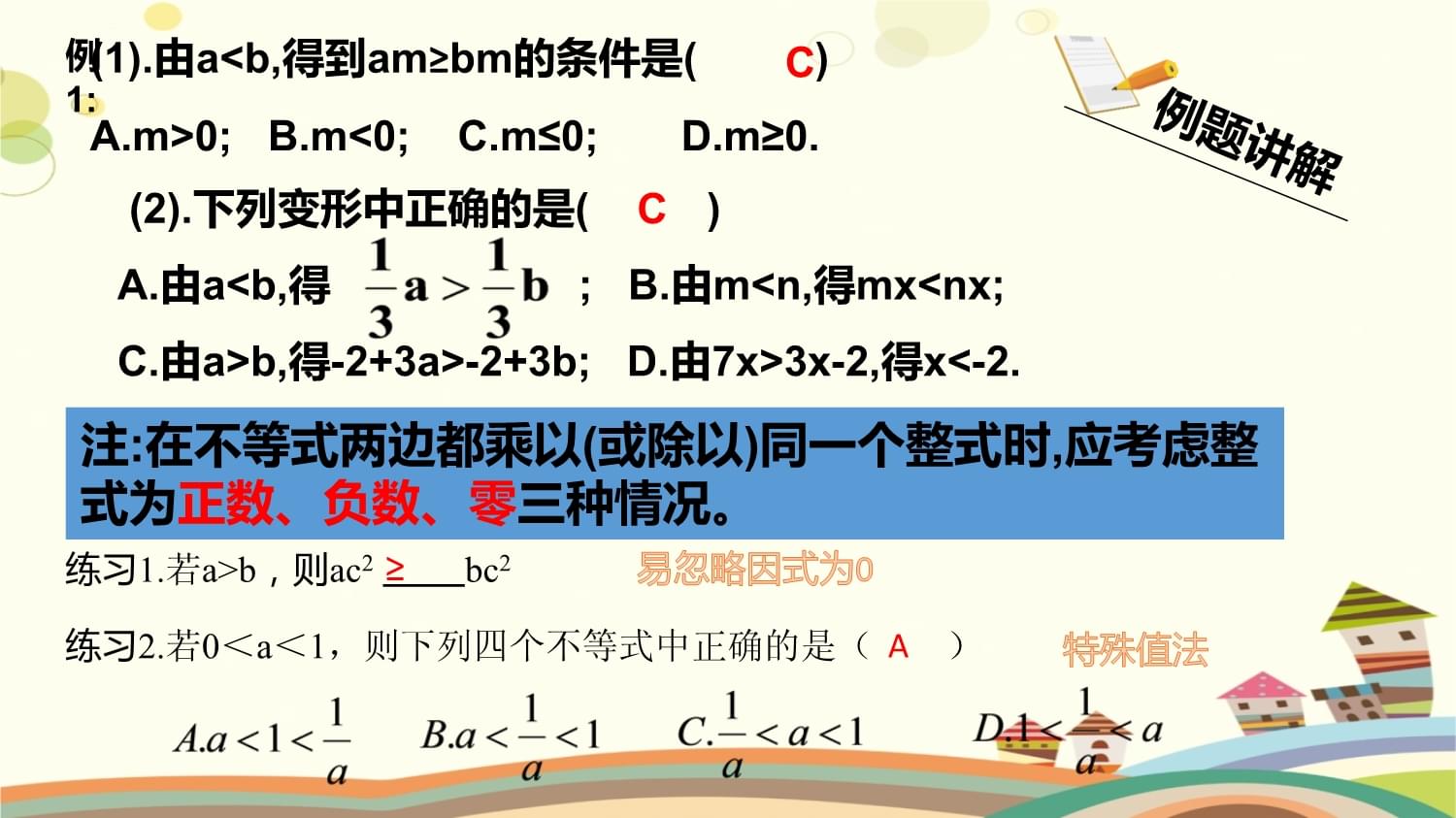
．知识归纳不等号不等式“≠”、“>”、“<”、“≥”、“≤”整式不变不变正数负数改变例1:(1).由a<b,得到am≥bm的条件是()A.m>0;B.m<0;C.m≤0;D.m≥0.C(2).下列变形中正确的是()A.由a<b,得;B.由m<n,得mx<nx;C.由a>b,得-2+3a>-2+3b;D.由7x>3x-2,得x<-2.C注:在不等式两边都乘以(或除以)同一个整式时,应考虑整式为正数、负数、零三种情况。练习2.若0＜a＜1，则下列四个不等式中正确的是（）练习1.若a>b，则ac2

bc2易忽略因式为0特殊值法例题讲解≥A3.一元一次不等式：只含有未知数，并且未知数的最高次数是，且不等式的两边都是，且的不等式叫做一元一次不等式．注：一元一次不等式的一般形式是ax+b>0或ax+b<0(a≠0，a，b为已知数)．(2)若是关于x的一元一次不等式，则m的取值是（）

例2（1）

下列各式中是一元一次不等式的是（）A．3x-2＞0B．2＞-5C．3x-2＞y+1D．3y+5＜一个1整式系数不等于0Am=1考点二：一元一次不等式（组）的解法4.(1)不等式的解:使不等式成立的未知数的值.知识归纳(2)不等式的解集：一个含有未知数的不等式的所有解，组成了这个不等式的解集。(3)解不等式：求不等式解集的过程其实质就是把不等式化为“x>a或x≥a或x<a或x≤a”的形式。(4)用数轴表示不等式的解集：x>ax<ax≥ax≤aaaaa大于向右画,小于向左画.解不等式的一般步骤：．①去分母；②去括号；③移项；④合并同类项；⑤化系数为1(5)一元一次不等式组定义：关于同一个未知数的几个一元一次不等式合在一起，就组成一个一元一次不等式组

;

不等式组的解集：一元一次不等式组中各个不等式的解集的

，叫做这个一元一次不等式组的解集.公共部分归纳、一元一次不等式组的解集及记忆方法同大取大的解集是当a＞b时，X＞aX＞bX＞a同小取小的解集是当a＞b时，X＜aX＜bX＜b大小小大取中间的解集是当a＞b时，X＜aX≥bb≤X＜a大小等同取等值X＝a的解集是X≥aX≤a不等式组大大小小解不了的解集是当a＞b时，X＞

aX＜

b无解文字记忆数学语言图形abababaab例题讲解．例1：若关于x的一元一次不等式组无解，则a的取值范围.例2：已知实数a是不等于3的常数，解不等式组：，并依据a的取值情况写出其解集．思考：形如这类不等式该怎么解？练习1.（1）已知关于x的不等式组有解，则a的取值范围是

.

（2）已知关于x的不等式组的整数解共有3个，则a的取值范是.2.(1)若不等式组的解集是,则

.

a<1-3≤a<-21（2）若关于x的不等式组的解集为，则a的取值范围是（）3.在方程组中,若未知数x,y满足x+y>0，则m的取值范围是().强化训练a≤-2m<3考点三：一元一次不等式与方程及函数的内在联系知识归纳（1）一次函数y=kx+b（k≠0）的图象是条直线,（2）kx+b=0（k≠0）是一元一次方程,其解为直线与x轴的交点的横坐标.（3）kx+b>0,kx+b<0（k≠0）是一元一次不等式,它们分别对应直线在x轴上方的部分和直线在x轴下方的部分,相应不等式的解集便是相应的图象对应的所有x值。例1.一次函数y1=kx+b的图象如图所示，则方程kx+b=0的解集一次函数y1=kx+b的图象如图所示，则不等式kx+b<0的解集。二次函数y2=ax2+bx+c的图象如图所示，则不等式y2<0的解集。一次函数y1=kx+b的图象如图所示，则不等式kx+b>2的解集。2当y1>y2时，x的取值范围例2：若关于t的不等式组，恰好有3个整数解，则关于x的一次函数

的图象与反比例函数的图象的公共点的个数。与一次函数，反比例函数的综合运用延伸训练1、关于x方程有两个相等的实数根，其中是锐角三角形ABC的一个内角，若关于y的方程的两个根恰好是三角形ABC的两边长，求三角形ABC的周长2.已知二次函数，当时，y的最大值为5，求a的值考点四：列一元一次不等式（组）解决实际问题解一元一次不等式（组）的应用步骤：①注意设未知数的方法，②找出问题中量与量之间的不等关系，③抽象出不等式（组），④求出不等式（组）的解集后，要注意验证解的合理性．正确理解列不等式（组）的关键词：如不少于、不超过、大于、小于、至少、至多、不足、不空、不满等．其中，不少于就是大于或等于表示为，不超过、至多都是不大于的意思，不大于就是小于或等于，表示为，非负数就是正数和零等．知识归纳例1：某市出租车的收费标准是：起步价5元（即行驶距离不超过2千米都需要付5元车费），超过2千米以后，每增加1千米，加收1.8元（不足1千米按1千米计），某同学从家乘出租车到学校，付了车费24.8元，求该同学的家到学校的距离在什么范围？解：设该同学的家到学校的距离是x千米，则：所以该同学的家到学校的距离在大于12小于等于13的范围例题讲解例2、某饮料厂为了开发新产品，用A、B丙种果汁原料各19千克、17.2千克试制甲、乙两种新型饮料共50千克，下表是实验的相关数据：(1)假设甲种饮料需配制千克,请你写出满足题意的不等式组,并求出其解集.(2)若甲种饮料每千克成本为4元,乙种饮料每千克成本为3元,设这两种饮料的成本总额为y元,请写出y与x的函数关系式(不要求写自变量的取值范围),并根据(1)的运算结果,确定当甲种饮料配制多少千克时,甲、乙两种饮料的成本总额最少？每千克会含量饮料A（单位：千克）B（单位：千克）甲乙0.50.20.30.4解：（1）由题意得：解不等式组，得（2）y=4x+3(50-x)，即y=x+150。因为x越小，y越小，所以当x=28时，y最小。即当甲种饮料配制28千克时，甲、乙两种饮料的成本总额最少。0.5x+0.2(50-x)≤190.3x+0.4(50-x)≤17.228≤x≤30练习1.有红、白两种颜色的小球若干个，已知白球的个数比红球少，但白球的个数的2倍比红球多；若给每个白球都写上数字“2”，给每个红球都写上数字“3”(每个小球只能写上一个数字)，结果所有小球写的数字总和为60，那么白球和红球各是多少个？解：设有红球x个（x为整数）则白球数为0.5(60-3x)

依题意有0.5(60-3x)<x<0.5(60-3x)×2解得12<x<15所以x可为13或14当x=13时，白球数为21/2=10.5不为整数，舍去当x=14时，白球数为18/2=9答：有白球9个，红球14个强化训练2.某商店将一件商品的进价提价20%的，以降价30%，以105元出售，问该商店卖出这件产品，是盈利还是亏损？3：某校在“五一”期间组织学生外出旅游，如果单独租用45座的客车若干辆，恰好坐满；如果单独租用60座的客车，可少租一辆，并且有一辆不空也不满。（1）求外出旅游的学生人数是多少？（2）已知45座客车座客车每辆租金250元，60座客车每辆租金300元，为了节省租金，并保证每个学生都能有座，决定怎样租用客车，使得租金最少？4：某单位急需用车，但以不准备买车，他们准备和一个个体车主或一国营出租车公司中一家签订月租车合同，设汽车每月行驶x千米，应付给个体车主有月租费用是y1元，应付给国营出租车公司的月租费用是y2元，y1、y2分别与x之间的函数关系（两条射线）如图所示，回答下列问题：（1）分别写出y1、y2与x的函数关系式？（2）每月行驶的路程在什么范围内，租国营出租车公司的车合算？在什么范围内租个体车主的车合算？（3）每月行驶的路程是多少千米时，租两家车的费用相同？（4）如果这个单位估计每月行驶的路程为2300米，那么这个单位租哪家的车合算？1000200030002500500100015002000x（千米）y(元）O强化训练1.下列各式中是一元一次不等式的是（）A．3x-2＞0 B．2＞-5C．3x-2＞y+1 D．3y+5＜2.在数轴上与原点的距离不大于3的点对应的x满足（）A.x＜3B.x≤3C-3＜x＜3D.-3≤x≤3DA要点导学要点二：不等式的性质问题1.若a＞b＞0则下列不等式不一定成立的是（）A.ac＞bcB.a＋c＞b＋cC.1÷a＜1÷bD.ab＞b²A1.若x+5＞0，则（）A.x+1＜0B.x-1＜0C.D.-2x＜122.已知a＜0，-1＜b＜0，则a、ab、ab²之间的大小关系是（）A.a＞ab＞ab²B.ab＞ab²＞aC.ab＞a＞ab²D.ab²＞a＞abDB强化训练要点导学要点三：解不等式及不等式组问题1：把不等式x+2＞4的解表示在数轴上，正确的是()A． B．C． D．B要点导学问题2：解不等式组解：解不等式①得，x＞2，解不等式②得，x≤4，在数轴上表示如下：所以，不等式组的解集是2＜x≤4．1.写出一元一次不等式组的所有自然数的解是

．2.解不等式组，并把解集在数轴上表示出来.0,1,2,3解：解不等式3x-2≤x，的x≤1.解不等式，得x＞-3.解集在数轴上表示如图：所以原不等式的解集为-3＜x≤1强化训练要点导学要点四：含参数的不等式（组）问题1：如果不等式组的整数解仅为1、2、3，那么适合这个不等式组的整数a、b的有序数对共有（）A.16对B.12对C.9对D.6对B1.若关于x的不等式组的整数解共有4个，则m的取值范围是(

)

A．6＜m＜7

B．6≤m＜7

C．6≤m≤7

D．6＜m≤72.关于x的不等式组的解集为x＜3，那么m的取值范围为（）A．m=3B．m＞3C．m＜3D．m≥3DD强化训练随堂检测1.某商贩去菜摊买黄瓜，他上午买了30斤，价格为每斤x元；下午，他又买了20斤，价格为每斤y元．后来他以每斤0.5（x+y）元的价格卖完后，结果发现自己赔了钱，其原因是（）A．x＜y

B．x≥y

C．x≤y

D．x≥y

2.若a＜b＜0，则式子：①；②；③；④中，正确的有（）A．1个 B．2个 C．3个 D．4个3.解集在数轴上表示为如图所示的不等式组是（）ACD0随堂检测4.不等式2x-7<5-2x的正整数解有()

A.1个B.2个C.3个D.4个5.关于x的不等式2x－a≤－1的解集如图所示，则a的取值是（）．A、0B、－3