广东省惠州市某学校2022-2023学年数学八上期末质量检测试题含解析

2022-2023学年八上数学期末模拟试卷

注意事项：

1.答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码

区域内。

2.答题时请按要求用笔。

3.请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效;

在草稿纸、试卷上答题无效。

4.作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。

5.保持卡面清洁，不要折暴、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题（每小题3分，共30分）

1.如图，若MB=ND,4MBA=NNDC,添加下列条件不能直接判定

AABM名KDN的是（）

A.AM=CNB.ZA-ZNCD

C.AB=CDD.ZM=ZN

2

2.若分3式r"_?7"的值为零,则x的值为（）

x—3

A.±3B.3C.-3D.9

3.现实世界中，对称现象无处不在，中国的方块字中有些也具有对称性，下列美术字

是轴对称图形的是（）

A.诚B.信C.友D.善

4.甲、乙二人做某种机械零件，甲每小时比乙多做6个，甲做90个所用的时间与做

60个所用的时间相等.设甲每小时做x个零件，下面所列方程正确的是（）

9060906090609060

A.B.—=C.—D.------=—

xx-6Xx+6x—6xx+6x

5.血是同类二次根式的是（)

C.JD.4

A.B.V12

V3V2

6.一次数学测试后，某班40名学生的成绩被分为5组，第1〜4组的频数分别为12、

10、6、8,则第5组的频率是（）

A.0.1B.0.2C.0.3D.0.4

7.近似数0.13是精确到（）

A.十分位B.百分位C.千分位D.百位

8.如果一个正多边形的内角和是外角和的3倍，那么这个正多边形的边数为（）

A.5B.6C.7D.8

9.小明学了利用勾股定理在数轴上作一个无理数后，于是在数轴上的2个单位长度的

位置找一个点D,然后过点D作一条垂直于数轴的线段CD,CD为3个单位长度，以原

点为圆心，0C的长为半径作弧，交数轴正半轴于一点，则该点位置大致在数轴上（）

A.2和3之间B.3和4之间C.4和5之间D.5和6之间

10.下列说法正确的是（）.

①若8=2。+!。，则一元二次方程办2+）x+c=o必有一根为-1.

2

②已知关于x的方程（攵—2）/+反1》+1=0有两实根，则k的取值范围是

③一个多边形对角线的条数等于它的边数的4倍，则这个多边形的内角和为1610度.

④一个多边形剪去一个角后，内角和为1800度，则原多边形的边数是11或11.

A.①③B.①②③C.②④D.②③④

二、填空题（每小题3分，共24分）

3x-y=mfx=l

11.关于x、y的方程组的解是，，则n-m的值为_____.

x+my=n［）'=1

12.如图，AB=AC,A3的垂直平分线交A3于点E,交AC于点。，若NA=4O°,

则=

13.若将3/一3+〃进行因式分解的结果为（3X+2）（X-1）,贝!）3=.

14.已知点A（x,4）到原点的距离为5,则点A的坐标为.

15.如图，在一个长为8cm,宽为5c机的长方形草地上，放着一根长方体的木块，它

的棱和草地宽4。平行且棱长大于AZ）,木块从正面看是边长为2c机的正方形，一只蚂

蚁从点A处到达点C处需要走的最短路程是

16.直角三角形斜边长是5,一直角边的长是3,则此直角三角形的面积为.

17.如图，在平面直角坐标系中，矩形A3CO的边CO、Q4分别在x轴、N轴上，点

E在边8C上，将该矩形沿4E折叠，点3恰好落在边OC上的尸处.若Q4=8,

CF=4,则点E的坐标是.

18.已知一次函数y=2x+〃的图像经过点A（2,y）和8（—1,%），则必%（填

“〉”、“<”或“=

三、解答题（共66分）

19.（10分）（1）问题发现:如图（1）,已知:在三角形AABC中，ZBAC=9Q\AB^AC,

直线/经过点A，瓦〃直线/,CEL直线/,垂足分别为点试写出线段8。,。石

和CE之间的数量关系为

（2）思考探究：如图（2）,将图（D中的条件改为：在AA5C中，AB=AC,D,A,E

三点都在直线I上，并且ZBDA=ZAEC=ABAC=a,其中a为任意锐角或钝角.请

问（1）中结论还是否成立？若成立，请给出证明；若不成立，请说明理由.

（3）拓展应用：如图（3）,2E是D,A,E三点所在直线机上的两动点，（力,A,E三

点互不重合），点尸为NS4c平分线上的一点，且AAB尸与A4CF均为等边三角形,

连接若N3D4=NAEC=Na4C,试判断ADEF的形状并说明理由.

20.(6分)已知：在平面直角坐标系中，点O为坐标原点，AAOB的顶点A的坐标为

(0,4),顶点3在x轴上(点8在点。的右侧)，点。在AB上，连接OC,且BC=OC.

(D如图1,求点。的纵坐标；

(2)如图2,点。在x轴上(点。在点。的左侧)，点尸在AC上，连接力/交。4于点E；

(3)如图3,在(2)的条件下，4G是AAQB的角平分线，点M与点8关于V轴对称，过

点M作分别交AQAC于点N,P,若DE=AB,EN=PC,求点£

的坐标.

A

DM

x

（图3）

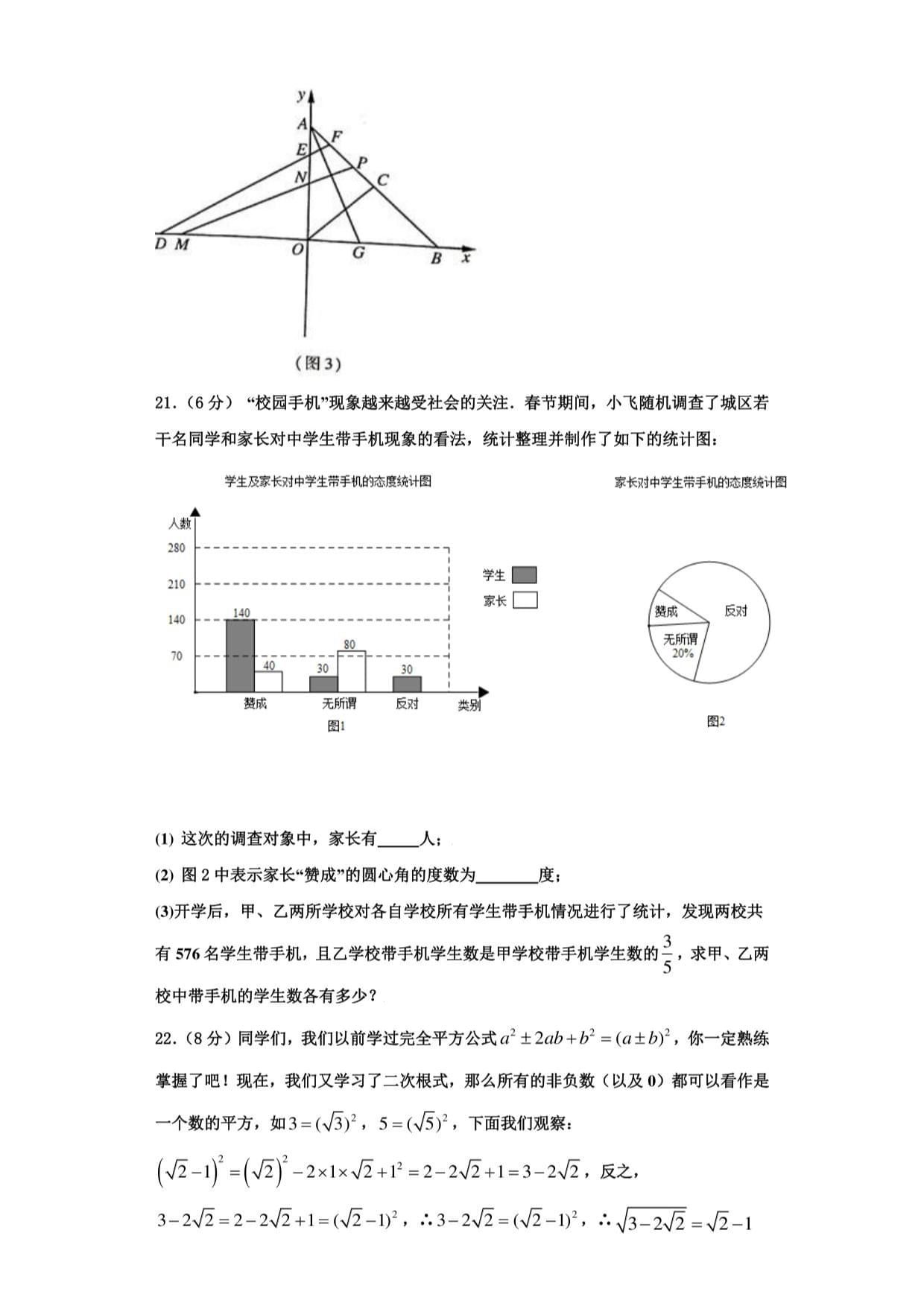
(1)这次的调查对象中，家长有人；

(2)图2中表示家长“赞成”的圆心角的度数为度；

⑶开学后，甲、乙两所学校对各自学校所有学生带手机情况进行了统计，发现两校共

3

有576名学生带手机，且乙学校带手机学生数是甲学校带手机学生数的《，求甲、乙两

校中带手机的学生数各有多少？

22.(8分)同学们，我们以前学过完全平方公式。2±2。匕+〃=(。±份2,你一定熟练

掌握了吧！现在，我们又学习了二次根式，那么所有的非负数(以及0)都可以看作是

一个数的平方，如3=(百/，5=(有/，下面我们观察：

(V2-1)2=(0『-2xlx0+『=2—20+1=3-2后，反之，

3-2夜=2-2亚+1=（正-I）?,.•.3-20=（0-1）2,353-20=0-1

求：⑴V3+2V2；

（2）-^4—VT25

（3）若-]a±2加=7^士〃,则"?、"与。、，的关系是什么？并说明理由一

23.（8分）如图，点尸在线段A8上，点E,G在线段CO上，FG//AE,Z1=Z1.

⑴求证：AB//CD,

（1）若尸6_13。于点”，3c平分NABO,ZD=111°,求N1的度数.

24.（8分）计算：（2血-1）2-（V24-V6）+G.

（x+2x—1Ax—4

25.（10分）已知丁丁——j——--——，请化简后在-4WXW4范围内选一个

[厂一2xx~-4x+4）x

你喜欢的整数值求出对应值.

26.（10分）计算下列各题：

（1）5/（—1）'->/25-1"^xV-27+（―2）'

（2）（2屈一64+3屈）+26

参考答案

一、选择题（每小题3分，共30分）

1、A

【分析】根据全等三角形的判定方法：SSS、SAS、ASA、AAS、HL,结合选项进行判

定，然后选择不能判定全等的选项.

【详解】A、添加条件AM=CN,仅满足SSA,不能判定两个三角形全等；

B、添加条件AB=CD,可用SAS判定△ABMdCDN；

C、添加条件NM=NN,可用ASA判定△ABMWACDN；

D、添加条件NA=NNCD,可用AAS判定△ABMg^CDN.

故选：A.

【点睛】

本题考查了三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、

ASA,AAS、HL.注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等

时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角.

2、C

【分析】根据分式的值为零的条件：分子=0且分母W0,即可求出结论.

【详解】解：•.•分式3三二27的值为零,

x-3

3d-27=0

：.<

x-3w0

解得：x=-3

故选C.

【点睛】

此题考查的是分式的值为零的条件，掌握分式的值为零的条件：分子=0且分母W0是解

决此题的关键.

3、D

【分析】根据轴对称图形的概念逐一进行分析即可得.

【详解】A.不是轴对称图形，故不符合题意；

B.不是轴对称图形，故不符合题意；

C不是轴对称图形，故不符合题意；

D.是轴对称图形，符合题意，

故选D.

【点睛】

本题考查了轴对称图形的识别，熟知“平面内，一个图形沿一条直线折叠，直线两旁的

部分能够完全重合的图形是轴对称图形”是解题的关键.

4、A

【解析】解：设甲每小时做x个零件，则乙每小时做G-6）个零件，由题意

60

得:-.故选A.

Xx-6

5、A

【分析】根据同类二次根式的定义，先将各选项化为最简二次根式，再看被开方数是否

相同即可.

【详解】解：A、与1=4垃,与后被开方数相同，是同类二次根式;

B、疵=26,与后被开方数不同，不是同类二次根式;

c、小|=半，与正被开方数不同，不是同类二次根式；

口、4=当'与血被开方数不同，不是同类二次根式.

故选：A.

【点睛】

此题考查的是同类二次根式的判断，掌握同类二次根式的定义是解决此题的关键.

6、A

【分析】根据第卜4组的频数求得第5组的频数'再根据频率=慧即可得到结论.

【详解】解：第5组的频数为：40-12-10-6-8=4,

4

.•.第5组的频率为：—=0.1,

40

故选：A.

【点睛】

此题主要考查了频数与频率，正确掌握频率求法是解题关键.

7、B

【分析】确定近似数精确到哪一位，就是看这个数的最后一位是什么位即可.

【详解】近似数0.13是精确到百分位，

故选B.

【点睛】

此题考查了近似数，用到的知识点是精确度，一个数最后一位所在的位置就是这个数的

精确度.

8、D

【分析】设正多边形的边数为n,利用多边形的内角和公式和外角和定理即可解答.

【详解】设正多边形的边数为n,由题意得：

（n-2）•180°=3X360°,

解得：n=8,

故选：D.

【点睛】

本题考查多边形的内角（和）与外角（和），熟记多边形的内角和公式及外角和为360。是

解答的关键.

9、B

【解析】利用勾股定理列式求出0C,再根据无理数的大小判断即可.

解答：解：由勾股定理得，℃=6+32=屈，

V9<13<16,

/.3<713<4,

...该点位置大致在数轴上3和4之间.

故选B.

“点睛”本题考查了勾股定理，估算无理数的大小，熟记定理并求出0C的长是解题的

关键.

10、A

【分析】①由8=2a+'c可得4a-lb+c=0,当x=-l时，4a-lb+c=0成立，即可判定；

2

②运用一元二次方程根的判别式求出k的范围进行比较即可判定;③设这个多边形的边

数为n,根据多边形内角和定理求得n即可判定；④分剪刀所剪的直线过多边形一个顶

点、两个顶点和不过顶点三种剪法进行判定即可.

【详解】解：①b=la+；c,则4a-lb+c=0,

一元二次方程ax2+bx+c=0必有一个根为-L故①说法正确；

②：伙—2）/+反1》+1=0有两实数根，

:原方程是一元二次方程.

:.k-2,0,k彳2,故②说法错误；

③设这个多边形的边数为n,

贝11」——^=4n

2

解得n=ll或0（舍去）

:这个多边形是11边形.

:这个多边形的内角和为：

(11-1)X180°=9X180O=1610°.

故③说法正确；

一个多边形剪去一个角的剪法有过多边形一个顶点、两个顶点和不过顶点三种剪法，会

有三个结果，故④错.

故选：A.

【点睛】

本题考查了一元二次方程的解和根的判别式以及多边形内角和定理，灵活应用所学知识

是正确解答本题的关键.

二、填空题(每小题3分，共24分)

11、1

【分析】根据方程组的解满足方程组，把解代入，可得关于m、n的二元一次方程组，

求解该方程组即可得答案.

x=l3x-y=mm=2

【详解】把1"弋入，得19

y=1x4-my=nl+m=n

m—2

求解关于m、n的方程组可得：\,故〃一加=3-2=1.

n-3

故答案为：1.

【点睛】

本题考查二元一次方程组，求解时常用代入消元法或加减消元法，其次注意计算仔细即

可.

12、1

【分析】根据等边对等角和三角形的内角和定理即可求出NABC,然后根据垂直平分线

的性质可得DA=DB,从而得出NA=NDBA=40°，即可求出ZDBC.

【详解】解:=AC,24=40°

二ZABC=ZACB=^(180°-NA)=70°

：DE垂直平分AB

.\DA=DB

：.ZA=ZDBA=40°

:.ZDBC=ZABC-ZDBA=1°

故答案为:1.

【点睛】

此题考查的是等腰三角形的性质和垂直平分线的性质，掌握等边对等角和线段垂直平分

线上的点到这条线段两个端点的距离相等是解决此题的关键.

13、-1

【分析】将(3x+l)(x-1)展开，J?!)3x1-mx+n=3xI-x-l,从而求出m、n的值，进一步

求得mn的值.

【详解】解：(3x+l)(x-1)=3x'-x-l,

J.3x1-mx+n=3x1-x-l,

m=l,n=-l,

/.mn="l.

故答案为-L

【点睛】

本题考查了因式分解的应用，知道因式分解前后两式相等是解题的关键.

14、(1,4)或(-1,4)

【分析】根据两点间的距离公式便可直接解答.

【详解】解：,••点A(x,4)到原点的距离是5,点到x轴的距离是4,

.*•5=7x2+42»解得x=l或x=-l.

A的坐标为(1,4)或(-1,4).

故答案填：(1,4)或(-1,4).

【点睛】

本题考查了勾股定理以及点的坐标的几何意义，解题的关键是明确横坐标的绝对值就是

点到y轴的距离，纵坐标的绝对值就是到x轴的距离.

15、13c，”.

【分析】解答此题要将木块展开，然后根据两点之间线段最短解答.

【详解】由题意可知，将木块展开，

相当于是AB+2个正方形的宽，

二长为8+2X2=12c/n；宽为5cm.

于是最短路径为：V52+122=13C//».

故答案为13cm.

本题考查了四边形中点到点的距离问题，掌握勾股定理是解题的关键.

16、1.

【解析】试题分析：•••直角三角形斜边长是5,一直角边的长是3,.•.另一直角边长为

V52-32=2-该直角三角形的面积S=；x3x2=l.故答案为1.

考点：勾股定理.

17、(-10,3)

【分析】由勾股定理可以得到CE、OF的长度，根据点E在第二象限，从而可以得到

点E的坐标.

【详解】设CE=a,则BE=8-a,

由题意可得，EF=BE=8-a,

VZECF=90°,CF=4,

a2+42=(8-a)2,

解得，a=3,

设OF=b,贝I]OC=b+4,

由题意可得，AF=AB=OC=b+4,

VZAOF=90°,OA=8,

b2+82=(b+4)2,

解得，b=6,

.*.CO=CF+OF=10,

.•.点E的坐标为(-10,3),

故答案为(-10,3).

【点睛】

本题考查勾股定理的应用，矩形的性质、翻折变化、坐标与图形变化-对称，解题的关

键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答.

18、＞

【分析】根据一次函数图象的增减性，结合函数图象上的两点横坐标的大小，即可得到

答案.

【详解】•••一次函数的解析式为：y=2x+b,

•••y随着x的增大而增大，

•.,该函数图象上的两点A(2,yJ和8(-1,%)，

V-l<2,

•*.yi>y2»

故答案为：>.

【点睛】

本题考查了一次函数图象上点的坐标特征，正确掌握一次函数图象的增减性是解题的关

键.

三、解答题(共66分)

19、(1)DE=CE+BD；(2)成立，理由见解析；(3)4DEF为等边三角形，理由见解

析.

【分析】(1)利用已知得出ZCAE=ZABD,进而根据AAS证明aABD与4CAE全等,

然后进一步求解即可；

(2)根据NBrJAuZAECuNBACna,得出NCAE=NABD,在4ADB与ACEA

中，根据AAS证明二者全等从而得出AE=BD,AD=CE,然后进一步证明即可；

(3)结合之前的结论可得4ADB与4CEA全等，从而得出BD=AE,ZDBA=ZCAE,

再根据等边三角形性质得出NABF=NCAF=60。，然后进一步证明4DBF与4EAF全

等，在此基础上进一步证明求解即可.

【详解】(1)直线/,CE_L直线/,

.,.ZBDA=ZAEC=90°,

AZBAD+ZABD=90",

VZBAC=90",

/.ZBAD+ZCAE=90",

二NCAE=NABD,

在△ABD与4CAE中，

VZABD=ZCAE,NBDA=NAEC,AB=AC,

:.AABD^ACAE(AAS),

；.BD=AE,AD=CE,

VDE=AD+AE,

.*.DE=CE+BD,

故答案为：DE=CE+BD；

(2)(1)中结论还仍然成立，理由如下：

：=ZBAC=a,

AZDBA+ZBAD=ZBAD+ZCAE=180°-a,

NCAE=NABD,

在AADB与aCEA中，

VZABD=ZCAE,ZADB=ZCEA,AB=AC,

.,.△ADB^ACEA(AAS),

.,.AE=BD,AD=CE,

.*.BD+CE=AE+AD=DE,

即：DE=CE+BD,

(3)ADEb为等边三角形，理由如下：

由(2)可知：△ADBgaCEA,

.♦.BD=EA,ZDBA=ZCAE,

VAABF与4ACF均为等边三角形，

.,.ZABF=ZCAF=60",BF=AF,

NDBA+NABF=NCAE+CAF,

二NDBF=NFAE,

在4DBF与AEAF中，

VFB=EA,NFDB=NFAE,BD=AE,

.,.△DBF^AEAF(SAS),

，DF=EF,NBFD=NAFE,

:.ZDFE=ZDFA+ZAFE=ZDFA+ZBFD=60°,

/.△DEF为等边三角形.

【点睛】

本题主要考查了全等三角形性质与判定的综合运用，熟练掌握相关概念是解题关键.

20、(1)点C的纵坐标为1；(1)证明见解析；(3)点E的坐标为(0,3).

【分析】(1)由BC=OC得出/BOC=NCBO,然后通过等量代换得出

ZAOC^ZOAC,则有AC=OC,进而有OK=AK=',则点C的纵坐标可

2

求;

(1)通过44。+"£'0=2/，4/力推导出/0七0=2/0。£,然后求出

ZDEO=60°,^ODE=30°,则利用含30。的直角三角形的性质即可证明结论；

(3)连接BN,过点8作BT//PN交丁轴于点T,先推出AP=QN,然后通过

垂直和角度之间的代换得出N/WP=NAPN则有AN=AP,然后进一步

AB=AT,再因为BN=BT,BO±NT得出AT的值，则可求出AB,DE,利用

即DE=2EO可求出OE的值，则点E的坐标可求.

【详解】(1)如图，过点。作CKLQ4于点K

QBC=OC

:.ZBOC=ZCBO

又QNAOC+ZBOC=90°,ZOAC+ZCBO=90°

:.ZAOC=ZOAC

AC-OC.

..OK=AK=LQA=2

2

.•.点C的纵坐标为1.

(1)QZACO+ZDEO=2ZAFE

：.NBOC+ZCBO+NDEO=2(ZCBO+NODE)

:./DEO=2/ODE

又QZDEO+/ODE=90°

NDEO=60°,NODE=30°

:.DE=2OE

(3)如图，连接8N,过点B作BT//PN交轴于点T

:.OE^AC

又QEN=PC

：.AP=ON

■:MP1AG

：.ZANP+ZNAG=90°,ZAPN+NPAG=90°,NNAG=NPAG

:.ZANP^ZAPN

：.AN=AP

,-.AN=ON=-OA=2

2

•••点M与点8关于,’轴对称，点N在＞轴上

:.MN=BN,NOIBM

：.ZBNO=ZMNO=ZANP

QBT//PN

ZBTN=ZANP=ZBNO,NABT=ZAPN

：.ZABT=ZBTN,BN=BT

：.AB=AT

QBN=BT,BOLNT

.-.OT=ON=2

AT=6

:.AB=DE=6

:.0E=3

•点E在y轴上，且在点。的上方.

.•.点£的坐标为（0,3）.

【点睛】

本题主要考查等腰三角形的性质，平行线的性质，含30°的直角三角形的性质，垂直

平分线的性质，掌握等腰三角形的性质，平行线的性质，含30°的直角三角形的性质,

垂直平分线的性质是解题的关键，第⑶问有一定的难度，主要是在于辅助线的作法.

21、(1)1；(2)36°；(3)甲：360,乙：216

【分析】（1）认为无所谓的有80人，占总人数的20%,据此即可求得总人数；

（2）赞成的人数所占的比例是：黑，所占的比例乘以360。即可求解；

（3）甲、乙两校中带手机的学生数分别有x、y人，根据两校共有2384名学生带手机,

3

且乙学校带手机的学生数是甲学校带手机学生数的-,即可列方程组，从而求解.

【详解】解：（1）家长人数为80・20%=1.

（2）表示家长“赞成”的圆心角的度数为黑乂360°=36°.

400

（3）设甲、乙两校中带手机的学生数分别有x、y人，

则由题意有

x+y=576

x=360

3，解得，

y=216

[-5

即甲、乙两校中带手机的学生数分别有360人，216人.

【点睛】

本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得

到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据；扇形统

计图直接反映部分占总体的百分比大小.

22、(1)V2+1；(2)6一1；(3)m+n=a,mn=b,理由见解析

【分析】（1）将3拆分为2+1,再根据完全平方公式和二次根式化简即可求解;

（2）将4拆分为3+1,再根据完全平方公式和二次根式化简即可求解；

（3）利用二次根式的性质结合完全平方公式直接化简得出即可.

【详解】解：（1）"+20

=«五+1『

=>/2+1；

(2)74-V12=7(73-I)2=73-1：