八年数学(十一章)学案课件

11.1全等三角形

一、学习目标

1、掌握全等形、全等三角形及相关概念和全等三角形性质。

2、理解“平移、翻折、旋转”前后的图形全等。

3、熟练确定全等三角形的对应元素。

二、自学指导

自学课本P2—3页，完成下列要求：

1、理解并背诵全等形及全等三角形的定义。

2、注意全等中对应点位置的书写。

3、理解并记忆全等三角形的性质。

4、自学后完成展示的内容，20分钟后，进行展示。

三、展示内容：

1、相同的图形放在一起能够o这样的两个图形叫做

2、能够的两个三角形叫做全等三角形。

3、一个图形经过—、—、―后位置变化了，但形状'大小都没有改变，

即平移、翻折'旋转前后的图形o

4、叫做对应顶点。叫做对应边。叫做

对应角。

5、全等三角形的对应边—。相等。

6、课本P4练习1、2

7、如图1,AABC^ADEF,对应顶点是,对应角是_

______________________,对应边是____________________________________

8、如图2,AABC^ACDA,AB和CD,BC和DA是对应边，写出其他对应

边及对应角__________________________________________________________

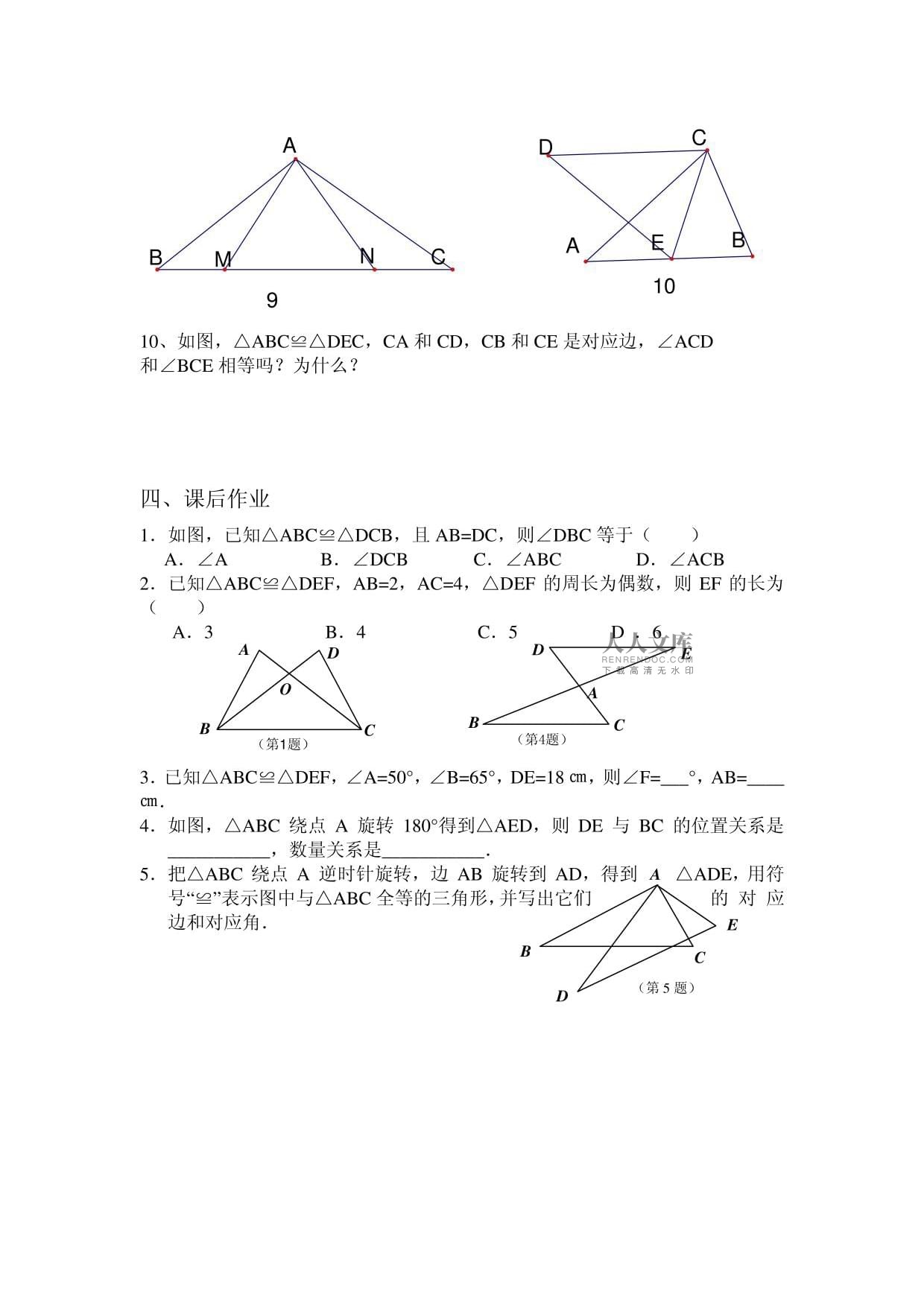
9、如图3,aABN之△ACM,NB=NC,AC=AB,则BN=,Z

BAN=,=AN,=ZAMC.

10、如图，AABC^ADEC,CA和CD,CB和CE是对应边，ZACD

和NBCE相等吗？为什么？

四、课后作业

1.如图，已知^ABC乌ADCB,且AB=DC,则NDBC等于（）

A.ZAB.ZDCBC.ZABCD.ZACB

2.已知AABC丝△DEF,AB=2,AC=4,ADEF的周长为偶数，则EF的长为

3.已知AABC叁ADEF,ZA=50°,NB=65°,DE=18cm,贝ijNF=—°,AB=

cm.

4.如图，4ABC绕点A旋转180。得到4人£口，则DE与BC的位置关系是

，数量关系是.

5.把4ABC绕点A逆时针旋转，边AB旋转到AD,得到AAADE,用符

号“g”表示图中与aABC全等的三角形，并写出它们的对应

边和对应角.\>E

B

（第题）

D5

11.2三角形全等的判定（1）

一、学习目标

1、掌握三角形全等的判定（SSS）

2、初步体会尺规作图

3、掌握简单的证明格式

二、自学指导

认真阅读课本P6—8页，完成下列要求:

1、小组讨论探究lo（1）满足一个或两个条件的两个三角形是否全等。（2）满

足3个条件时，两个三角形是否全等。注意分类。

2、小组讨论探究2,交流合作，初步体会尺规作图（具体按第7页画图步骤）

3、掌握三角形全等的判定之一（SSS）

4、自主学习例1,初步体会证明的基本过程，并会利用判定（SSS）进行简单的

推理，注意过程格式。

5、利用判定（SSS）作一个角等于已知角，具体按第8页作法的具体步骤。

6、自学后完成展示的内容，20分钟后，进行展示。

三、展示内容：1、P8,练习

2、如图，AB=AD,CB=CD,求证：△ABCgZ\ADC

3、如图C是AB的中点,AD=CE,CD=BE,

求证：△ACDg/\CBE

4、如图，AD=BC,AC=BD,

求证：(1)ZDAB=ZCBA(2)ZACD=ZBDC

5、如图，已知点B、E、C、F在同一条直线上，AB=DE,

AC=DF,BE=CF,

求证：（1）AABC^ADEF

（2）AB〃DE

四、课后作业

1.如果△ABC的三边长分别为3,5,7,△OEE的三边长分别为3,3%—2,

2x-l,若这两个三角形全等，则x等于（）

7

A.-B.3C.4D.5

3

2.如图，已知AC=DB,M^AABC^ADCB,还需知道的一个条件是

3.已知AC=FD,BC=ED,点B,D,C,E在一条直线上，要利用“SSS”，还需

添加条件,得△ACB且a.

4.如图4ABC中，AB=AC,现想利用证三角形全等证明NB=NC,若证三角形

全等所用的公理是SSS公理，则图中所添加的辅助线应是

5.如图，A,E,C,尸在同一条直线上，AB=FD,BC=DE,AE=FC.

求证：△ABgXEDE.B

A/x\

AECF

（第5题）

6.如图，AB=AC,BD=CD,那么N6与NC是否相等？为什么%°

/D

AB

（第6题）

11.2全等三角形的判定(2)

一、自学目标：

1、会画一个三角形与已知三角形全等(根据两边与夹角对应相等)

2、理解并掌握边角边的判定方法

3、利用边角边判定方法解决实际问题

4、探究具备“SSA”条件的两个三角形是否全等？

二、自学指导

认真阅读课本第8—10页的内容，完成下列要求：

1、小组合作学习探究2,注意画图时的规范，用尺规作图注意画法。

2、通过画图发现规律：的两个三角形全等。

3、认真学习例2后，我们得到：在证明两个三角形中线段相等或角相等时通常

通过证明来解决。

4、自学后完成展示的内容，20分钟后，进行展示。

三、展不内容：

1、如图1已知4ABF与aDCE中，NB=NC,BE=CF,AB=CD,则a

_

A.P.A.

/X/\

/\/\

B

--

B/ZAV一D.

12

2、如图2已知AB=AC,AD=AE,NBAC=NDAE,

求证：△ABDgZSACE

证明：VZBAC=ZDAE()

ZBAC+=ZDAE+

即NBAD=NCAE

在4ABD和4ACE中

__________________(____________)

__________________(____________)

__________________()

二()

3、如图要测量工件内槽宽，可以把两根钢条的中点连在一起，做成一个工具，

只要测量出的长，就是内槽的宽，为什么？

4、如图AB=AC,AD=AE,求证：(1)ZB=ZC(2)NBDC=NBEC

四、课后作业

1.如图，AB=AC,如果根据“SAS”使4ABE丝AACD,那么需添加条件

2.如图，AB〃CD,BC〃AD,AB=CD,BE=DF,图中全等三角形有

对.

3.下列命题：①腰和顶角对应相等的两个等腰三角形全等；②两条直角边对应

相等的两个直角三角形全等；③有两边和一角对应相等的两个三角形全等；

④等腰三角形顶角平分线把这个等腰三角形分成两个全等的三角形.其中正

确的命题有.

4.已知：如图，C是A6的中点，AD//CE,

求证:/XADC^/XCEB.

5.如图,A,C,D,6在同一条直线上，AE=BF,

求证:FD//EC.

B（第5题）

11.2全等三角形的判定(3)

一、学习目标：

1、掌握全等三角形的判定方法一“ASA”“AAS”。

2、理解并运用“ASA”“AAS”解决相关问题。

二、自学指导：

1、自学课本U—12页内容，完成下列要求：

2、认真学习探究5的内容，按照课本提示的操作步骤动手操作，完成后,

归纳探究5反映的规律。

3、认真阅读探究6,合作探究：要运用-“ASA”证明“两角和其中一角的

对边对应相等的两个三角形全等”关键点是什么。

4、学习例3,考虑要证明△ACD^^ABE还需要的条件。

5、自学后完成要展示的内容，-20分钟后进行展示。

三、展示内容：

1、指导2反映的规律是：的两个三角形全等。

简写为：“"、或“

2、指导3中关键点是：______________________________________

3、完成课本13页1一2题。

4、归纳三角形全等的判定方法：

5、如图：D在AB上，E在AC上，DC=EB,

ZC=ZB

求证：(1)AACDgAABE

(2)AC=AB

四、课后作业

1.下列说法正确的是()

A.有三个角对应相等的两个三角形全等

B.有一个角和两条边对应相等的两个三全等

C.有两个角和它们夹边对应相等的两个三角形全等

D.面积相等的两个三角形全等

2.如图，ZB=ZDEF,BC=EF,要证△ABCgADEF,

（1）若以“SAS”为依据，还缺条件；

（2）若以“ASA”为依据，还缺条件.

（第2题）

3.如图，在^ABC中，BD=EC,NADB=NAEC,

NB=NC,则NCAE=.

4.已知：如图，AB〃CD,OA=OC.求证：OB=OD

（第4题）

（笫5题）

6.已知：如图，AB=AD,BO=DO,求证：AE=AC

BD

（第6题）

11.2全等三角形的判定HL的判定（4）

一、学习目标

1、掌握RT△特殊的判定方法：HL判定方法

2、能够用HL判定方法来判定两个RT△全等

二、自学指导

认真13阅读一14页内容，要求掌握以下内容

1、前面学习的判定方法，直角三角形是否还能用？

2、理解画RTZ\A,B,C,的过程，并由这个过程得出RT△的判定方法:

___________________，简称________

3、在学习探究时，一定要动手画图呀！

4、学习例4,想一想，要证BC=AD,需要证明什么？

1.使两个直角三角形全等的条件是（）

A.一个锐角对应相等B.两个锐角对应相等

C.一条边对应相等Do一直角边和斜边对应相等

2.如图，BE和CF是△45C的高，它们相交于点0,且8E=C£>,则图中有对

全等三角形，其中能根据“HL”来判定三角形全等的有

3.已知:如图，AC=DF,BF=CE,

求证:AB=DE

4.如图,△ABC中，。是5C边的中点，A。平分NBA。，OE_LA8于E,DF1.

AC于E

求证：(1)DE=DF；(2)ZB=ZC.

5.如图，AO为△ABC的高，E为AC上一点，BE交AD于点F,且有8F=AC,

FD=CD.

求证：BELAC.

IL3角的平分线的性质

一、学习目标

1、分用改尺规画出一个角的平分线（会说作法）

2、理解并掌握角平分线的性质

3、感受证明一个儿何命题的方法与步骤

二、自学指导

1、自学课本19页（10分钟）

（1）说出探究中AE是NDAE的平分线的理由

（2）作图时要读一步画一步

2、自学20—21页思考前的内容（6—10分钟）

（1）独立动手完成探究，从而得出角平分线的性质：角的平分线上的点

（2）注意体会角平分线的性质这个命题是如何画出图形，写出已知、求证的。

三、展示内容

P19页练习

1、已知NA0B的角平分线0C,点P在0C上，且点P到OA的距离为4cm,则点P

到边OB的距离是___B

2、如图在AABC中，ZC=90°,AD平分NBAC,BC=10cm,\

BD=6cm,贝ij点D至AB的距离为\

△ABC中，AB=AC,M为BC中点，MDLAB于D,ME±AC

于E,求证：MD=ME

BMc

已知aABC内，ZABC,ZACB的角平分线交于点P,

且PD、PE、PF分别垂直于BC、AC、AB于D、E、F

三点，求证：PD=PE=PF

四、课后作业

1.用尺规作已知角的平分线的理论依据是（）

A.SASB.AASC.SSSD.ASA

2.如图，0P平分NAOB,PD10A,PE1OB,垂足分别为D,E,

下列结论错误的是（）

A.C.ZDPO=ZEPOD.PD=OD

（第3题）

（第2题）

3.如图，在AABC中，NC=90。，AD是NBAC的角平分线，若BC=5cm,

BD=3cm,则点D到AB的距离为cm.

4.已知：如图，AM是NB4。的平分线，。是AM上一点，过点。分别作AB,

AC的垂线，垂足为凡D,且分别交AC、AB于点、G,E.E/B

5.如图，AO平分NBAC,OEL46于点E,UAC于点口，且8。=。.

求1正：BE=CF.

6.如图，ZVIBC中，ZC=90°,AD是△ABC的角平分线，DE±AB于E,AD=BD.

（1）求证：AC=BE；（2）求的度数。

（第6题）

1L3角的平分线的判定

一、学习目标：

1、掌握角平分线的判定

2、会运用角平分线的判定解决简单的问题。

二、自学指导：

认真学习课本21—22页的内容，完成下列要求：

1、找出角平分线判定的题设与结论,并与角平分线性质的题设和结论进

行比较。

2、合作探究“思考”部分的内容：要确定集贸市场的准确位置（1）根

据角平分线的判定，能否确定集贸市场在公路与铁路夹角的平分线

上。（2）再依据集贸市场离两路交叉处的距离。

3、认真学习例题，注意辅助线的作法。

4、自学后，完成展示内容，20分钟后进行展示。

三、展示内容：

1、课本22页练习。

2、角的内部的点在角的平分线上。

3、如图（教材21页11.3-6）,AABC的角平分线BM、CN交于点P,求证：点

P到4ABC三边的距离相等。

证明：过点P作PDLAB于D,PE，BC于E,PF，AC于F。（把辅助线补充完整）

•；BM是AABC的角平分线，点P在BM上

APD=_____________o

同理：PE=~.

PD==.

即点P到三边AB、BC、CA的距离相等。

4、求证：角的内部到角的两边距离相等的点，在角的平分线上。

已知：如图，PDLAB于D,PEL—于E,PD=.点P在0C上。

求证：ZA0C=

证明：

D

1c

EBAC

5

5、在AABC中，外角NCBD和NBCE的平分线BF、CF相交于点F.

求证：点F也在NBAC的平分线上。

（提示：过点F作AD、BC、AE的垂线段FN、FM、FP,然后证FN=FP）

四、课后作业

1.三角形中到三边距离相等的点是（）

A.三条边的垂直平分线的交点B.三条高的交点

C.三条中线的交点D.三条角平分线的交点

2.如图，Z\ABC中，AB=AC,AD是4ABC的角平分线，DE1AB于点E,

DF_LAC于点F,有下面四个结论：①DA平分NEDF；②AE=AF；③AD上

的点到B,C两点的距离相等；④至IJAE,AF的距离相等的点到DE,DF的

距离也相等.其中正确的结论有（）

3.如图，在AABC串户为NBAC的平分线，DE_LAB于E,DFLAC于F,

△ABC面积是28cm2,AB=20cm,AC=8cm,则DE的长为_____cm.

4.已知：如图，BD=CD,CFLAB于点F,BELAC于点E.

求证：AD平分NBAC.

三角形的全等练习题

一、选择题

1.已知4ABC的六个元素，则下面甲、乙、丙三个三角形中和4ABC全等的

图形是（）

A.甲和乙B.乙和丙C.只有乙D.只有

丙

二、填空题

2.如图，已知NA=ND,NABC=NDCB,AB=6,则DC=.

3.如图，已知NA=NC,BE〃DF,若要用“AAS”证4ABE丝Z\C