浙江省衢州市3年（2020-2022）中考数学试卷真题分类汇编-02填空题

浙江省衢州市3年（20202022）中考数学试卷真题分类汇编-02

填空题

一.平方差公式（共1小题）

1.（2020•衢州）定义aXb=a（b+\）,例如2X3=2义（3+1）=2X4=8.则（x-1）※》

的结果为.

二.二次根式有意义的条件（共1小题）

2.（2021•衢州）若心I有意义，则x的值可以是.（写出一个即可）

三.二次根式的乘除法（共1小题）

3.（2022•衢州）计算（V2）2=.

四.一元一次方程的解（共1小题）

4.（2020•衢州）一元一次方程2x+l=3的解是x=.

五.一元二次方程的解（共1小题）

5.（2022•衢州）将一个容积为360c”的包装盒剪开铺平，纸样如图所示.利用容积列出图

中x（cm）满足的一元二次方程：（不必化简）.

4----------------20cm----------►

———国—

六.解一元一次不等式（共1小题）

6.（2021•衢州）不等式2（y+1）Vy+3的解集为.

七.反比例函数系数k的几何意义（共1小题）

7.（2022•衢州）如图，在△ABC中，边AB在x轴上，边4C交y轴于点E.反比例函数y

=K（x>0）的图象恰好经过点C,与边BC交于点D若AE=CE,CD=2BD,S^ABC

X

=6,则k=.

八.反比例函数图象上点的坐标特征（共2小题）

8.（2021•衢州）将一副三角板如图放置在平面直角坐标系中，顶点A与原点O重合，AB

在x轴正半轴上，且AB=4j§,点E在4。上，DE=1AD,将这副三角板整体向右平

4

移个单位，C,E两点同时落在反比例函数y=K的图象上.

9.（2020•衢州）如图，将一把矩形直尺ABC。和一块含30°角的三角板EFG摆放在平面

直角坐标系中，AB在x轴上，点G与点A重合，点厂在AQ上，三角板的直角边EF交

8C于点M,反比例函数y=K（x>0）的图象恰好经过点F,M.若直尺的宽CD=3,

X

三角板的斜边FG=8向，则％=.

10.（2020•衢州）小慧用图1中的一副七巧板拼出如图2所示的“行礼图”，已知正方形A5CZ）

的边长为4dm,则图2中〃的值为dm.

图1图2

一十.勾股定理的应用（共1小题）

11.（2020•衢州）图1是由七根连杆链接而成的机械装置，图2是其示意图.已知O,P两

点固定，连杆PA=PC=\40cm,AB=BC=CQ=QA=60cm,OQ=50cm,O,P两点间

距与OQ长度相等.当0Q绕点。转动时，点A,B,C的位置随之改变，点2恰好在线

段MN上来回运动.当点B运动至点M或N时，点A,C重合，点P,Q,A,B在同一

直线上（如图3）.

（1）点P到MN的距离为cm.

（2）当点P,0,A在同一直线上时，点Q到MN的距离为cm.

一十一.多边形内角与外角（共1小题）

12.（2021•衢州）如图，在正五边形A8CDE中，连结AC,BD交于点F,则/4F8的度数

为

D

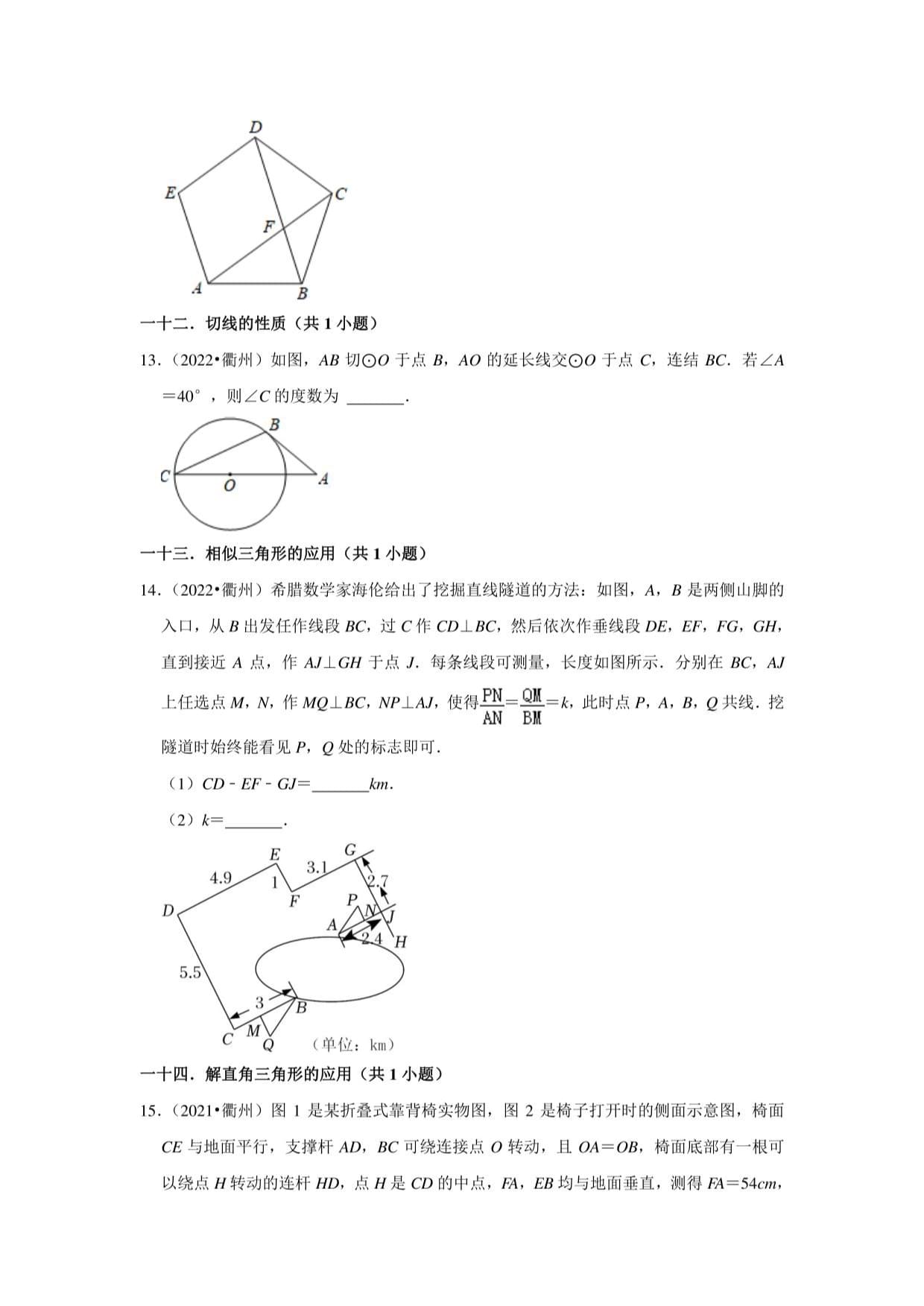
13.（2022•衢州）如图，AB切00于点B,A。的延长线交。。于点C,连结BC.若/A

一十三.相似三角形的应用（共1小题）

14.（2022•衢州）希腊数学家海伦给出了挖掘直线隧道的方法：如图，A,3是两侧山脚的

入口，从8出发任作线段BC,过C作CD_LBC,然后依次作垂线段OE,EF,FG,GH,

直到接近A点，作A/LG4于点J.每条线段可测量，长度如图所示.分别在BC,AJ

上任选点M,N,作MQLBC,NP上AJ,使得型=典=匕此时点尸，A,B,Q共线.挖

ANBM

隧道时始终能看见P,。处的标志即可.

（1）CD-EF-GJ=km.

15.（2021•衢州）图1是某折叠式靠背椅实物图，图2是椅子打开时的侧面示意图，椅面

CE与地面平行，支撑杆A。，BC可绕连接点。转动，且椅面底部有一根可

以绕点”转动的连杆HD，点”是CD的中点，FA,E8均与地面垂直，测得必=54。〃?,

EB=45cm,AB=4Scm.

（1）椅面CE的长度为,

（2）如图3,椅子折叠时，连杆绕着支点4带动支撑杆AD,BC转动合拢，椅面和

连杆夹角NCH。的度数达到最小值30°时，A,8两点间的距离为cm（结果精

确到0.1cm）.

（参考数据：sinl5°七0.26,cosl5°«0.97,tan15°g0.27）

图1图2图3

一十五.中位数（共2小题）

16.（2021•衢州）为庆祝建党100周年，某校举行“庆百年红歌大赛”.七年级5个班得分

分别为85,90,88,95,92,则5个班得分的中位数为分.

17.（2020•衢州）某班五个兴趣小组的人数分别为4,4,5,x,6.已知这组数据的平均数

是5,则这组数据的中位数是

一十六.概率公式（共1小题）

18.（2022•衢州）不透明袋子里装有仅颜色不同的4个白球和2个红球，从袋子中随机摸出

一球，“摸出红球”的概率是

浙江省衢州市3年（2020-2022）中考数学试卷真题分类汇编-02

填空题

参考答案与试题解析

一.平方差公式（共1小题）

1.（2020•衢州）定义〃※6=a（b+1）,例如2X3=2X（3+1）=2X4=8.则（x-1）※彳

的结果为7-I.

【解答】解：根据题意得：

（X-I）※彳=（X-1）（JC+1）=/-1.

故答案为：X2-1.

二.二次根式有意义的条件（共1小题）

2.（2021•衢州）若后I有意义，则x的值可以是2（答案不唯一）.（写出一个即可）

【解答】解：由题意可得：

x-120,

即X21.

则X的值可以是大于等于1的任意实数.

故答案为：2（答案不唯一）.

三.二次根式的乘除法（共1小题）

3.（2022•衢州）计算（&）2=2.

【解答】解：原式=2.

故答案是2.

四.一元一次方程的解（共1小题）

4.（2020•衢州）一元一次方程2x+l=3的解是x=1.

【解答】解；将方程移项得，

2%=2,

系数化为1得，

x=I.

故答案为：1.

五.一元二次方程的解（共1小题）

5.（2022•衢州）将一个容积为3605？的包装盒剪开铺平，纸样如图所示.利用容积列出图

中xCem）满足的一元二次方程：15x（10-x）=360（不必化简）.

【解答】解：由题意可得：长方体的高为：15cm,宽为：（20-2x）4-2Cem）,

则根据题意，列出关于x的方程为：15x（10-x）=360.

故答案为：15x（10-x）=360.

六.解一元一次不等式（共1小题）

6.（2021•衢州）不等式2（y+1）<>+3的解集为y<l.

【解答】解：2（y+1）<y+3

2y+2<y+3>

2y-y<3-2

y<l,

故答案为：><1.

七.反比例函数系数k的几何意义（共1小题）

7.（2022•衢州）如图，在△ABC中，边AB在x轴上，边AC交），轴于点E.反比例函数y

=K（x>0）的图象恰好经过点C,与边BC交于点D若4E=CE,CD=2BD,SMBC

X

=6,则k=—,

【解答】解：如图，作于点M,DNLAB于点、N,

m

则OM=m,CM=—,

m

VOE//CM,AE=CE,

・AO=AE_j

**OMEC，

J.AO=m,

■:DN〃CM,CD=2BD,

ABN=DN=BD=1,

・•丽CMBC

・,.ON=JL,

3m

的纵坐标为K,

3m

•・•k—k,

3mx

•»x—3m,

即0N=3m,

:.MN=2m,

BN—m9

.\AB=5m9

,**S^ABC=6,

.\5/ne—•4=6，

m2

5

故答案为：12.

5

A.反比例函数图象上点的坐标特征（共2小题）

8.（2021•衢州）将一副三角板如图放置在平面直角坐标系中，顶点4与原点O重合，AB

在x轴正半轴上，且AB=4j§,点E在AO上，DE=1AD,将这副三角板整体向右平

移12-、/个单位,C,E两点同时落在反比例函数y=K的图象上.

【解答】解：：48=4加，

:.BD=aAB=12,

：.C（4愿+6,6）,

-：DE=^AD,

4

的坐标为（3代，9）,

设平移t个单位后，则平移后C点的坐标为（4代+6+f,6）,平移后E点的坐标为（3如+/,

9）,

•.•平移后C,£两点同时落在反比例函数y=K的图象上，

X

（4«+6+f）X6=（3次+力X9,

解得f=12-代，

故答案为12-V3.

9.（2020•衢州）如图，将一把矩形直尺ABC。和一块含30°角的三角板EFG摆放在平面

直角坐标系中，AB在x轴上，点G与点A重合，点尸在AD上，三角板的直角边EF交

BC于点M,反比例函数y=K（x>0）的图象恰好经过点尸，M.若直尺的宽C£>=3,

X

三角板的斜边FG=«,则k=4073.

【解答】解：过点“作MNLA。，垂足为M则MN=C£>=3,

在RtZ\FMN中，/MFN=30°,

:.FN=MMN=3M，

:.AN=MB=8如-3禽=5«,

设0A=无，则。8=1+3,

：.F（X,8百），M（x+3,54），

又•.•点八M都在反比例函数的图象上，

；.8我尸（x+3）X5«,

解得，x=5,

：.F（5,8百），

；.k=5X8百=40禽.

故答案为：40,\/3.

九.七巧板（共1小题）

10.（2020•衢州）小慧用图1中的一副七巧板拼出如图2所示的“行礼图”，已知正方形ABC。

的边长为4dm,则图2中〃的值为（4+J?）dm.

图1图2

【解答】解：；正方形A8CZ）的边长为4M7,

•••②的斜边上的高是2dm,④的高是1力"，⑥的斜边上的高是1dm,⑦的斜边上的高是

.•.图2中人的值为（4+&）dm.

一十.勾股定理的应用（共1小题）

11.（2020•衢州）图1是由七根连杆链接而成的机械装置，图2是其示意图.已知。，P两

点固定，连杆B4=PC=140cm,AB=BC^CQ^QA=60cm,OQ=50crc,O,P两点间

距与OQ长度相等.当OQ绕点。转动时，点A,B,C的位置随之改变，点B恰好在线

段MN上来回运动.当点B运动至点M或N时，点A,C重合，点P,Q,A,8在同一

直线上（如图3）.

（1）点P到MN的距离为160cm.

（2）当点P,O,4在同一直线上时，点。到MN的距离为_衅__（?如

【解答】解：（1）如图3中,延长P0交MN于T,过点0作OHLPQ于H.

图3

由题意：。尸=OQ=50cro,140-60=80(cm),PM=PA+BC=140+60=

200Cem),PTYMN,

,：OHYPQ,

：.PH=HQ=40(cm),

VcosZP=^H.=^I.,

OPPM

•40=PT.

"50200，

：.PT=\6Q(an),

：.点P到MN的距离为160cm,

故答案为160.

(2)如图4中，当。，P,A共线时，过。作QH_LPT于”.设/M=xon.

:M

由题意A7=P7-出=160-140=20(cm),OA=PA-OP=140-50=90(。")，OQ=50c〃?,

AQ=60cm,

•/QHA.OA,

：.QH2=A(^-AH-=OQ1-OH2,

A602-?=502-(90-x)2,

解得x=侬，

9

.".HT=AH+AT=^-(cm),

9

.•.点Q到MN的距离为理C7».

9

故答案为我.

9

多边形内角与外角(共1小题)

12.（2021•衢州）如图，在正五边形ABCQE中，连结AC,B。交于点凡则/AF8的度数

为72°

【解答】解：•••五边形A8CDE是正五边形，

ZBCD=ZABC=__108»；

5

'：BA=BC,

：.ZBAC=ZBCA=36a,

同理NC8£>=36°,

二NAFB=NBCA+NCBD=TT,

故答案为：72°.

一十二.切线的性质（共1小题）

13.（2022•衢州）如图，AB切。。于点B,A。的延长线交0。于点C,连结BC若/A

=40°,则/C的度数为25°.

是。。切线,

OBLAB,

：.ZABO=90°,

；NA=40°,

AZAOB=90°-ZA=50°,

,?OC=OB,

；./C=N08C,

ZAOB=ZC+ZOBC,

：.ZC=25°.

故答案为：25°.

一十三.相似三角形的应用（共1小题）

14.（2022•衢州）希腊数学家海伦给出了挖掘直线隧道的方法：如图，A,8是两侧山脚的

入口，从B出发任作线段BC,过C作CC8C,然后依次作垂线段OE,EF,FG,GH,

直到接近A点，作AJ1GH于点J.每条线段可测量，长度如图所示.分别在BC,AJ

上任选点N,作MQ_LBC,NP_LAJ,使得理=旦旦=大，此时点P,A,B,。共线.挖

ANBM

隧道时始终能看见P,。处的标志即可.

（1）CD-EF-GJ=1.8km.

由矩形性质得：AZ^CD-EF-

BZ=DE+FG-CB-AJ=4.9+3.1-3-2.4=2.6,

:点P,A,B,Q共线，

：.ZMBQ^ZZBA,

又；/BMQ=NBZ4=90°,

:.XBMQsWZA,

.QM=4=AZ=1.8=9

"BMBZ获13,

故答案为：1.8；-

13

一十四.解直角三角形的应用（共1小题）

15.（2021•衢州）图1是某折叠式靠背椅实物图，图2是椅子打开时的侧面示意图，椅面

CE与地面平行，支撑杆A。，BC可绕连接点。转动，且OA=OB,椅面底部有一根可

以绕点〃转动的连杆“。，点”是C。的中点，FA,E8均与地面垂直，测得胡=54cm,

EB—45cm,AB=48cm.

（1）椅面CE的长度为40an.

（2）如图3,椅子折叠时，连杆绕着支点，带动支撑杆A。，8c转动合拢，椅面和

连杆夹角NC”。的度数达到最小值30°时，A,B两点间的距离为12.5cvn（结果精

确至1J0.1C/M）.

（参考数据：sinl5°~0.26,cosl50-0.97,tanl据-0.27）

G

图1图2图3

【解答】解：（1）,：CE//AB,

；.NECB=NABF,

tanZECB=tanNABR

•・•BE=—AF,

CEAB

•・•-4--5-=--5--4,

CE48

.•.C£=40(cm),

故答案为：40；

(2)如图2,延长AD,BE交于点M

'：OA=OB,

：.ZOAB=ZOBA,

在△A8F和△BAN中，

，Z0BA=Z0AB

，AB=AB>

ZFAB=ZABN=90°

.♦.△ABF也△BAN(ASA),

：.BN=AF=54(.cm),

:.EN=9Cem),

NEBN

•.•DE_48>

954

：.DE=S(cm),

：.CD=32(cm),

•点”是CO的中点，

:.CH=DH=16(an),

'：CD//AB,

：.△AOBs^DOC,

.C0=CD=32=2^

,,QBAB483"

如图3,连接CQ,过点H作“PLC。于P,

图3

'：HC=HD,HPLCD,

：.ZPHD=XZ