导数的概念及求导法则

关于导数的概念及求导法则第1页，共74页，2023年，2月20日，星期三(1).切线问题:求曲线在点处的切线第一节导数的概念另一点沿曲线趋向点时,割线的极限位置1导数的定义所谓曲线在其上点处的切线,是指当上第2页，共74页，2023年，2月20日，星期三

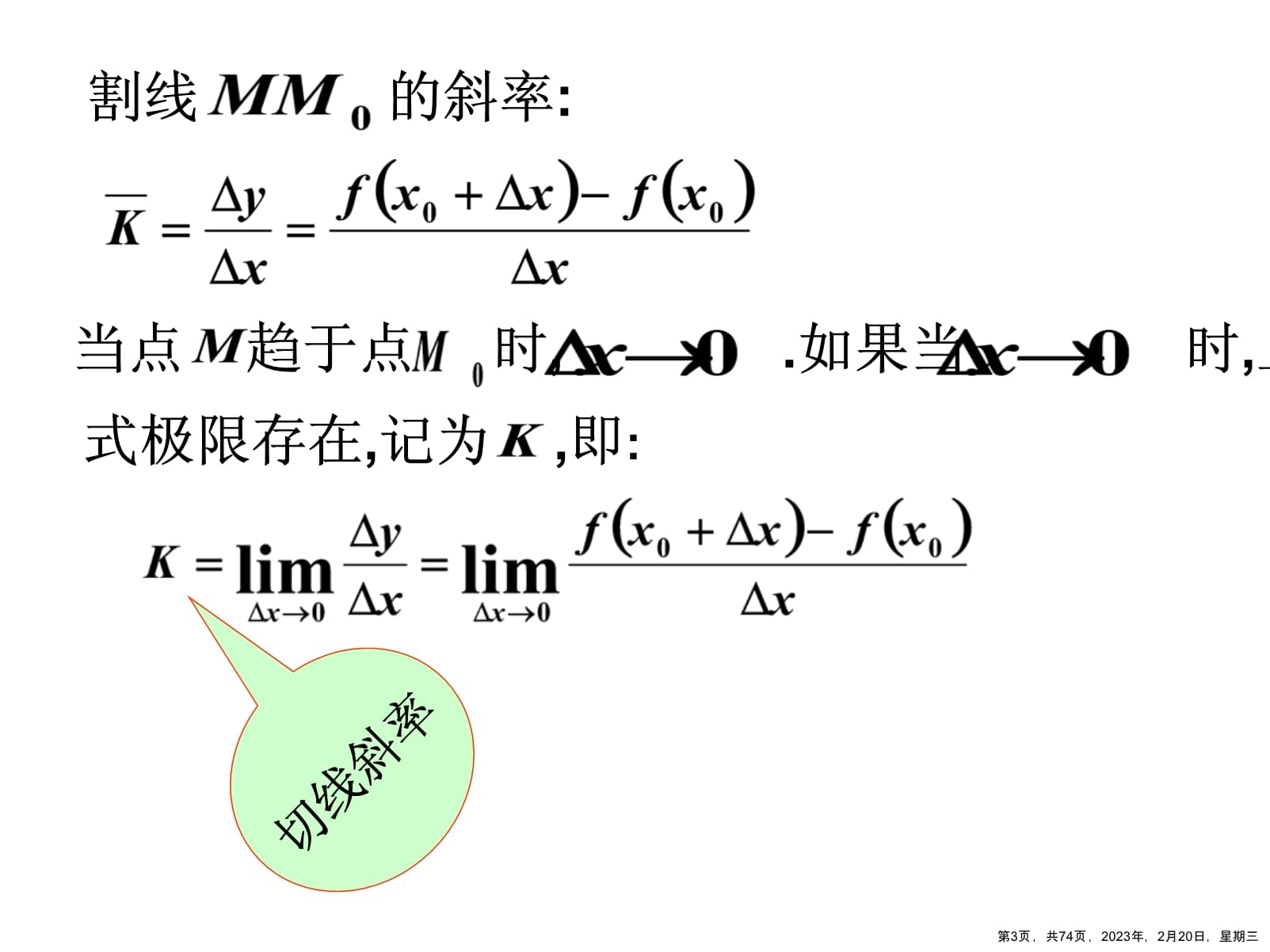
割线的斜率:当点趋于点时,.如果当时,上式极限存在,记为,即:切线斜率第3页，共74页，2023年，2月20日，星期三(2).变速直线运动的瞬时速度问题在时刻到的时间间隔内,平均速度如果当时,上式的极限存在,则设一物体作变速直线运动，运动的位置函数为,求在时刻的瞬时速度。第4页，共74页，2023年，2月20日，星期三定义1.1（导数）或若极限不存在,则称在处不可导。第5页，共74页，2023年，2月20日，星期三2.为方便起见，当时,也称在点处的导数为无穷大.第6页，共74页，2023年，2月20日，星期三3.左导数:右导数:函数在处可导若左极限存在，类似定义右导数此极限值称为左导数，并称f

在处左可导，记作：第7页，共74页，2023年，2月20日，星期三此时对区间I内的任一点,都对应着的一个确定的导数值,于是就构成了I上一个新的函数,这个函数称为原来函数

的导函数,记为即:若函数f在区间I

内的每一点处都可导(若I包含端点，则在左端点右可导，右端点处左可导），则称函数f在区间I上可导。第8页，共74页，2023年，2月20日，星期三例1.求函数(为常数)的导数.解:即:例2.求(为正整数)的导数.解:第9页，共74页，2023年，2月20日，星期三一般地,当为任意实数时,上面的公式也成立.即:第10页，共74页，2023年，2月20日，星期三例3.求的导数,及它在处的导数.解:即:类似可得:第11页，共74页，2023年，2月20日，星期三例4.求 的导数.解:即:特别地:例5.第12页，共74页，2023年，2月20日，星期三例6.解:注：左右导数是研究分段函数在分段点可导与否的有效工具。第13页，共74页，2023年，2月20日，星期三例7.设 ,求解:第14页，共74页，2023年，2月20日，星期三第15页，共74页，2023年，2月20日，星期三曲线在点处的切线的斜率。2.导数的几何意义：曲线在点处的左侧（右侧）切线的斜率。若函数f在处不可导，但单侧导数存在，则第16页，共74页，2023年，2月20日，星期三例10.求曲线在点处的切线和法线方程解:切线斜率:切线方程为:即:法线方程为:即:第17页，共74页，2023年，2月20日，星期三例11．讨论函数在点处的连续性和可导性及相应的曲线在点处切线的存在性。第18页，共74页，2023年，2月20日，星期三即 存在,于是由 ,得:3.可导与连续的关系定理1.1这表明, 在处连续.设函数 在处可导，第19页，共74页，2023年，2月20日，星期三左可导左连续右可导右连续区间I上可导区间I上连续逆命题不成立：亦有处处连续但处处不可导的函数。第20页，共74页，2023年，2月20日，星期三例13.解:第21页，共74页，2023年，2月20日，星期三第22页，共74页，2023年，2月20日，星期三第二节求导的基本法则1.基本初等函数的求导公式第23页，共74页，2023年，2月20日，星期三2.四则运算定理2.1设函数 在点处可导,则函数在点处也可导,且

第24页，共74页，2023年，2月20日，星期三证明:仅证（3）第25页，共74页，2023年，2月20日，星期三注:和与积的导数公式可以推广到任意有限多个函数.例如:第26页，共74页，2023年，2月20日，星期三例1.求下列函数的导数：解:第27页，共74页，2023年，2月20日，星期三第28页，共74页，2023年，2月20日，星期三类似地可得例2. ,求解:第29页，共74页，2023年，2月20日，星期三类似地可得例3.解:例4.解:故第30页，共74页，2023年，2月20日，星期三例5.解:第31页，共74页，2023年，2月20日，星期三定理2.2设函数在区间上单调连续，2.反函数的求导法则2:定理表明反函数的导数等于直接函数在相应点处的导数的倒数

注1:后面将证明若在I上，则f是I上的单调连续函数。第32页，共74页，2023年，2月20日，星期三解: 的反函数为于是解:第33页，共74页，2023年，2月20日，星期三同理可得:的反函数为于是第34页，共74页，2023年，2月20日，星期三定理2.3(链式法则）或3.复合函数的求导法则第35页，共74页，2023年，2月20日，星期三证明：第36页，共74页，2023年，2月20日，星期三即:注：此为求导法则中最重要的公式，可推广到任意有限个情形。应用时要看清复合层次，求导时要由外向内逐层求导，不重复，不遗漏。第37页，共74页，2023年，2月20日，星期三例8 ,求.例9解:解第38页，共74页，2023年，2月20日，星期三例10.求下列函数的导数:解(1)当时,因而当时,第39页，共74页，2023年，2月20日，星期三第40页，共74页，2023年，2月20日，星期三例11.求下列函数的导数:第41页，共74页，2023年，2月20日，星期三第42页，共74页，2023年，2月20日，星期三其中 可导.第43页，共74页，2023年，2月20日，星期三4.初等函数的求导问题一切初等函数的求导问题都解决，可导的初等函数的导函数仍为初等函数。基本的求导公式表：第44页，共74页，2023年，2月20日，星期三第45页，共74页，2023年，2月20日，星期三例12.求下列函数的导数:第46页，共74页，2023年，2月20日，星期三第47页，共74页，2023年，2月20日，星期三此为对数求导法，当所求导的函数为连乘积函数或幂指函数时，可考虑用此法。第48页，共74页，2023年，2月20日，星期三习题2.1P.87-892.(4)3.4.6.8.10.(1)11.(1)(3)(4)(5)(6)12.(2)(4)13141623.(2)(4)(5)(6)(9)(12)(14)(15)(19)(20)(21)24.(2)(3)第49页，共74页，2023年，2月20日，星期三5.高阶导数或 或即:如果的导函数在处可导，第50页，共74页，2023年，2月20日，星期三类似地定义的二阶导数在点的导数为或 或在点的三阶导数,记作:一般地,的阶导数在点的导数称为在点的阶导数(简称为阶导数),记作:或 或第51页，共74页，2023年，2月20日，星期三二阶及二阶以上的导数统称为高阶导数,函数第52页，共74页，2023年，2月20日，星期三例13.求下列函数的阶导数:解:一般地,可得:第53页，共74页，2023年，2月20日，星期三特别,特别,第54页，共74页，2023年，2月20日，星期三一般地,可得:类似地,可得:第55页，共74页，2023年，2月20日，星期三定理2.4第56页，共74页，2023年，2月20日，星期三例14.,求.解:设 则于是,第57页，共74页，2023年，2月20日，星期三解:例15.求下列函数的n阶导数:第58页，共74页，2023年，2月20日，星期三例16.解:p2x,16cos)1()2(xxynn--=第59页，共74页，2023年，2月20日，星期三6.隐函数求导法显函数隐函数链式法则第60页，共74页，2023年，2月20日，星期三例17第61页，共74页，2023年，2月20日，星期三解：方程两边对求导，得：在点处切线斜率法线斜率因此所求切线与法线方程分别为

与例18第62页，共74页，2023年，2月20日，星期三解：应用隐函数的求导法,得上式两边再对求导,得:例19第63页，共74页，2023年，2月20日，星期三7.由参数方程确定的函数的求导法则第64页，共74页，2023年，2月20日，星期三第65页，共74页，2023年，2月20日，星期三求解:例20.设第66页，共74页，2023年，2月20日，星期三故所求的切线方程为：与相对应的点为例21.已知三叶玫瑰线时，求曲线上相应点处的切线方程。解：第67页，共74页，2023年，2月20日，星期三8.相关变化率（自学内容）相关变化率第68页，共74页，2023年，2月20日，星期三

例22.一气球从离开观察员500米处离地面铅直上升其速率为140米/秒。当气球高度为500米时，观察员视线的仰角增加率是多少？解：设气球上升t

秒后其高度为

h，观察员的仰角其中都是时间t的函数。第69页，共74页，2023年，2月20日，星期三上式两边对t

求导，得：即观察员视线的仰角增加率是0.143弧度/秒