初中数学北师大版七年级下册第二章相交线与平行线“黄冈杯”一等奖

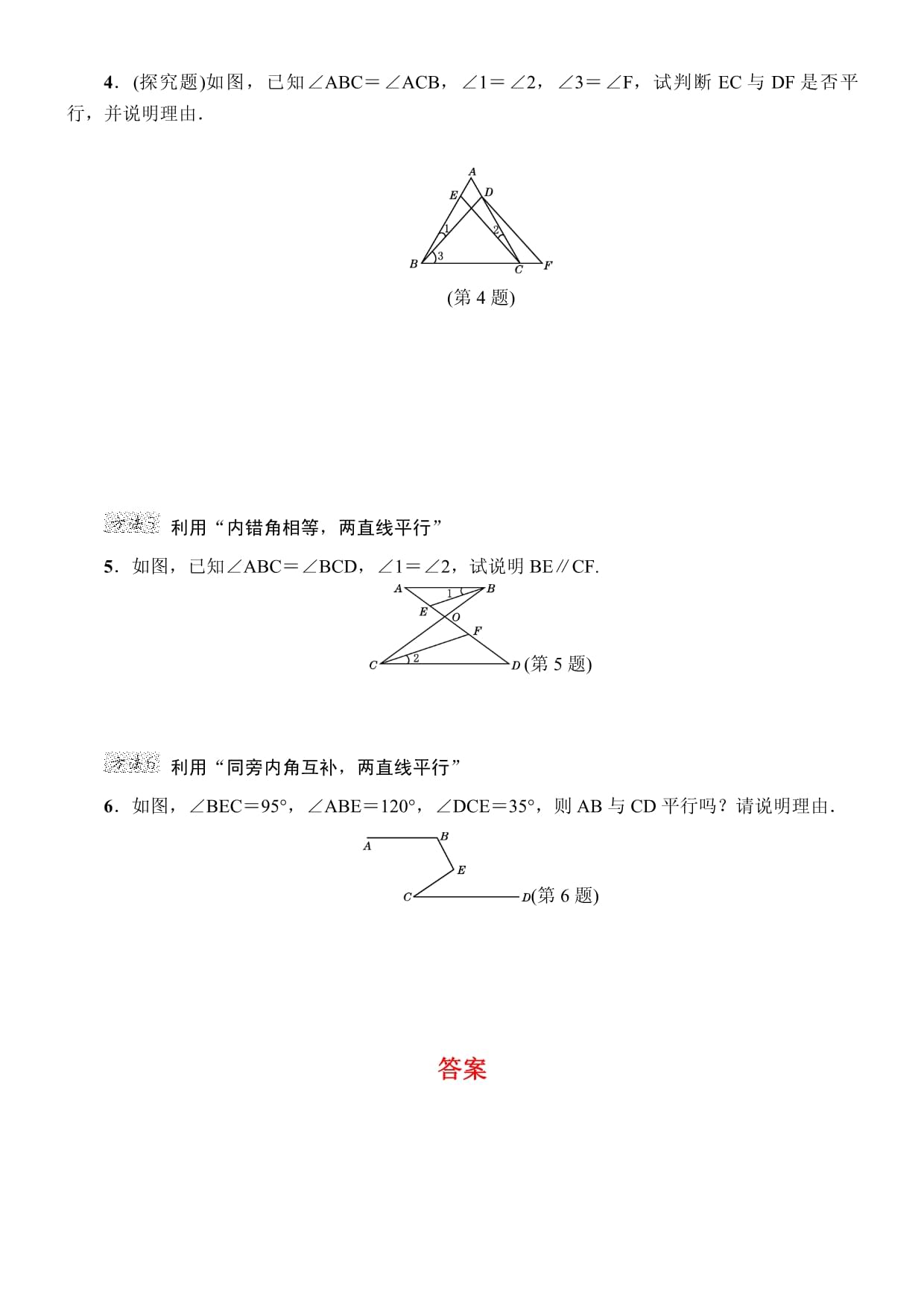
专训1识别相交线中的几种角名师点金：我们已经学习了对顶角、余角、补角和“三线八角”，能够准确地识别这几种角，对我们以后的学习起着铺垫作用．识别“三线八角”中的两个角属于何种类别时可联想英文大写字母，即“F”形的为同位角，“Z”形的为内错角，“U”形的为同旁内角，每类角都有一个共同点，即：有两条边在截线上，另外两条边在被截直线上．识别对顶角1．下列选项中，∠1与∠2互为对顶角的是()2．如图，直线AB，CD相交于点O，OE，OF是过点O的射线，其中构成对顶角的是()(第2题)A．∠AOF和∠DOEB．∠EOF和∠BOEC．∠BOC和∠AODD．∠COF和∠BOD识别余角、补角3．如图，直线AB与CD相交于点O，∠AOE＝90°，则∠1和∠2的关系是()A．互为对顶角B．互补C．相等D．互余(第3题)(第4题)4．如图，∠1的补角是()A．∠BOFB．∠AOC和∠BODC．∠BODD．∠BOF和∠BOD5．如图是由两块三角板拼成的图形，在直角顶点处构成了3个锐角，这三个锐角中互余的角是____________，相等的角是________．(第5题)6．如图，A，O，B三点在同一直线上，∠AOD＝∠DOB＝∠COE＝90°.(1)图中∠2的余角有____________，∠1的余角有________．(2)请写出图中相等的锐角，并说明理由．(3)写出∠1的补角，∠2有补角吗？若有，请写出来．(第6题)识别同位角、内错角、同旁内角7．如图，试判断∠1与∠2，∠1与∠7，∠1与∠BAD，∠2与∠9，∠2与∠6，∠5与∠8各对角的位置关系．(第7题)8．如图，请结合图形找出图中所有的同位角、内错角和同旁内角．(第8题)专训2活用判定两直线平行的六种方法名师点金：1.直线平行的判定方法很多，我们要根据图形的特征和已知条件灵活选择方法．2．直线平行的判定常结合角平分线、对顶角、邻补角、垂直等知识．利用平行线的定义1．下面几种说法中，正确的是()A．同一平面内不相交的两条线段平行B．同一平面内不相交的两条射线平行C．同一平面内不相交的两条直线平行D．以上三种说法都不正确利用“平行于同一条直线的两直线平行”2．如图，已知∠B＝∠CDF，∠E＋∠ECD＝180°.试说明AB∥EF.(第2题)利用“同垂直于第三条直线的两直线平行(在同一平面内)”3．如图，在三角形ABC中，CE⊥AB于点E，DF⊥AB于点F，DE∥CA，CE平分∠ACB，试说明∠EDF＝∠BDF.(第3题)利用“同位角相等，两直线平行”4．(探究题)如图，已知∠ABC＝∠ACB，∠1＝∠2，∠3＝∠F，试判断EC与DF是否平行，并说明理由．(第4题)利用“内错角相等，两直线平行”5．如图，已知∠ABC＝∠BCD，∠1＝∠2，试说明BE∥CF.(第5题)利用“同旁内角互补，两直线平行”6．如图，∠BEC＝95°，∠ABE＝120°，∠DCE＝35°，则AB与CD平行吗？请说明理由．(第6题)答案eq\a\vs4\al(专训1)1．D5．∠1与∠2，∠2与∠3；∠1与∠36．解：(1)∠1，∠3；∠2，∠4(2)∠1和∠3都是∠2的余角，根据同角的余角相等得∠1＝∠3，∠2和∠4都是∠1的余角，根据同角的余角相等得∠2＝∠4.(3)∠1的补角是∠BOC，∠2有补角，是∠AOE.7．解：∠1与∠2是同旁内角，∠1与∠7是同位角，∠1与∠BAD是同旁内角，∠2与∠9没有特殊的位置关系，∠2与∠6是内错角，∠5与∠8互为对顶角．8．解：(1)当直线AB，BE被AC所截时，所得到的内错角有：∠BAC与∠ACE，∠BCA与∠FAC；同旁内角有：∠BAC与∠BCA，∠FAC与∠ACE.(2)当AD，BE被AC所截时，内错角有：∠ACB与∠CAD；同旁内角有：∠DAC与∠ACE.(3)当AD，BE被BF所截时，同位角有：∠FAD与∠B；同旁内角有：∠DAB与∠B.(4)当AC，BE被AB所截时，同位角有：∠B与∠FAC；同旁内角有：∠B与∠BAC.(5)当AB，AC被BE所截时，同位角有：∠B与∠ACE；同旁内角有：∠B与∠ACB.eq\a\vs4\al(专训2)1．C点拨：根据定义判定两直线平行，一定要注意前提条件“同一平面内”，同时要注意在同一平面内，不相交的两条线段或两条射线不能判定其平行．2．解：因为∠B＝∠CDF，所以AB∥CD(同位角相等，两直线平行)．因为∠E＋∠ECD＝180°，所以CD∥EF(同旁内角互补，两直线平行)，所以AB∥EF(平行于同一条直线的两直线平行)．3．解：因为DF⊥AB，CE⊥AB，所以DF∥CE.所以∠BDF＝∠DCE，∠EDF＝∠DEC.因为DE∥CA，所以∠DEC＝∠ACE.因为CE平分∠ACB，所以∠ACE＝∠DCE.所以∠DCE＝∠DEC.所以∠EDF＝∠BDF.4．解：EC∥DF，理由如下：因为∠ABC＝∠ACB，∠1＝∠2，所以∠3＝∠ECB.又因为∠3＝∠F，所以∠ECB＝∠F.所以EC∥DF(同位角相等，两直线平行)．5．解：因为∠ABC＝∠BCD，∠1＝∠2，所以∠ABC－∠1＝∠BCD－∠2，即∠EBC＝∠FCB，所以BE∥CF(内错角相等，两直线平行)．(第6题)6．解：AB∥CD，理由如下：如图，延长BE，交CD于点F，则直线CD，AB被直线BF所截．因为∠BEC＝95°，所以∠CEF＝180°－95°＝85°.又因为∠DCE＝35°，所以∠BFC＝180°－∠DCE－∠CEF＝180