Ch8-6 位移电流 电磁场基本方程的积分形式

第八章电磁感应定律

电磁场位移电流一、随时间变化的磁场感生电场(涡旋电场)？随时间变化的电场电场和磁场应该对称！

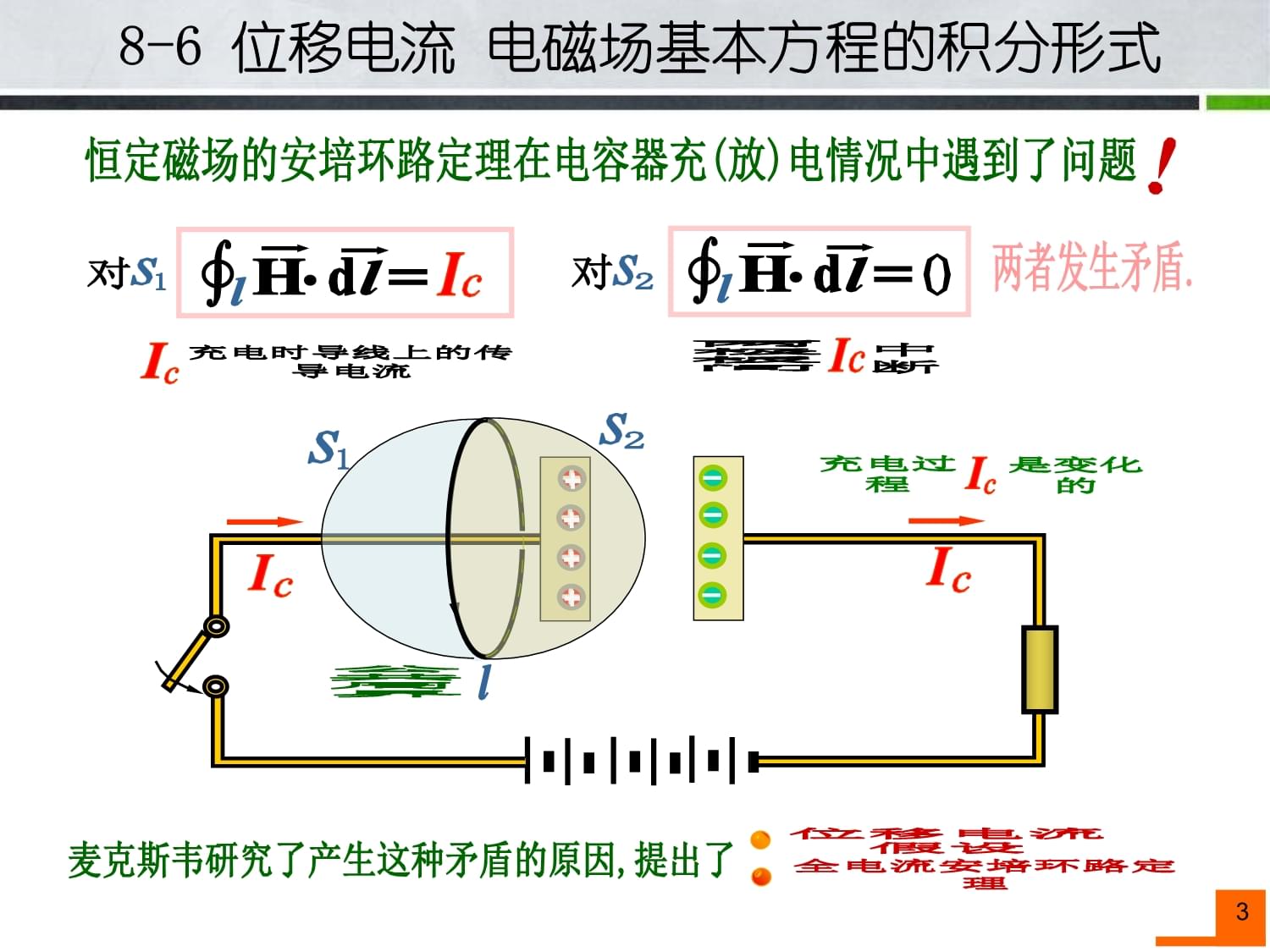
英国物理学家，经典电磁理论的奠基人，气体动理论创始人之一。治学严谨，擅长数学。他提出了有旋场和位移电流的概念,建立了经典电磁理论,并预言了以光速传播的电磁波的存在。和谐、完美、统一、对称麦克斯韦J.C.Maxwell2恒定磁场的安培环路定理在电容器充(放)电情况中遇到了问题！++++IcIc2s对0ldHl中断Ic两极板间对s1充电时导线上的传导电流IcIcldHl麦克斯韦研究了产生这种矛盾的原因,提出了位移电流假设全电流安培环路定理两者发生矛盾.充电过程

Ic是变化的s1l2s公共周界3Ic传导电流传导电流密度cjD电位移数值(线的密度)D极板带电量q都在变注意:两极板间虽然没有传导电流,但有变化的电场.电位移线的密度随着极板电荷的增多而变密.充电过程t1++Ic1D1cj1q1q1+2t++++Ic2D2cj2q2q2+4充电过程中某时刻，t则FDtddqtdd电场中也具有电流的量纲与等量值,并Ic传导电流Icqtdd电路中s作封闭面，s由高斯定理sFDDdsq解决了电流连续性问题麦克斯韦提出了位移电流的概念：若把右端电通量的时间变化率看作为一种电流，则电路连续。拓展了安培环路定理++++IcDcjqq+5位移电流等于通过该截面电位移通量对时间的变化率.定义充电过程中某时刻tFDtddqtddIDIc位移电流位移电流FDtddIDeDtejD位移电流密度某一点位移电流密度等于该点Ic++++IcDqq+qtdd

ID在有电容器的电路中，极板表面中断了的传导电流，由位移电流继续下去，两者一起构成电流的连续性。6全电流安培环路定理二、全电流传导电流+位移电流定义:ScjdS+SdSeDteIDIcsI+ScjdS+SDjdS比较位移电流仅由变化的电场所引起,它既可沿导体传播,也可脱离导体不产生焦耳热.在真空中传播,但IDIc传导电流是由运动的电荷产生,在导体中传播时会产生焦耳热.传导电流只在导体中存在；7ldHlIDIcsI+全电流对恒定和非恒定情况均适用.Ic0在两极板间ldlHIDdsteeDSDlIc充电过程SS'解决了恒定磁场的安培环路定理在电容器充(放)电情况中的矛盾！重大意义:表明传导电流位移电流都能产生磁场物理本质：激发（变化）磁场（变化）电场8三、位移电流的磁场性质：右旋的涡旋场ldlHdsteeDSldlEdsteeBSEteeB左旋涡旋场HteeD右旋涡旋场对称美9回顾麦克斯韦先后的两个重要发现变化的磁场感生电场LdlEBdtFdmBdssdtdsdtdBdsB()t0BddtEBB变化的电场变化的磁场D()t0DddtHsDtdsddldlHdtFdDDdssdtd四、麦克斯韦的电磁场理论10(中年)麦克斯韦(1831-1879)在充满变化的电场空间同时也充满变化的磁场,变化的电场和变化的磁场相互激发、相互依存电场和磁场的统一体称为电磁场都只不过是电磁场的两种特殊的表现形式稳恒磁场静电场和如果不考虑介质吸收电磁场能量,则电场与磁场之间的相互转化过程会永远循环下去,形成相互联系在一起的不可分割的统一的电磁场运动,并由近及远地传播出去形成电磁波。预言：11麦克斯韦对高斯定理电场环路定理磁场高斯定理环路定理的推广1.推广后的电场环路定理ldlE+ldlE静ldlE感0+((stBdseestBdsee空间任一点的电场强度麦克斯韦认为:静EE+E感空间任一点的电位移矢量静DD+D感122.推广后的电场高斯定理感SdSD静SdSD+SdSDSqi+0SqidVrV对于电荷连续分布带电体3.推广后的磁场高斯定理无论稳恒磁场或变化电场产生的磁场都是无源场SdSB04.推广后的磁场环路定理也就是我们前面已经讨论过的全电流安培环路定理ldHlIDIcsI+ScjdS+SdSeDte((Scj+eDteSd131.电场环路定理ldlEstBdsee2.电场高斯定理SdSDdVrV3.磁场高斯定理SdSB04.磁场环路定理ldHl((Scj+eDteSd麦克斯韦方程组(积分形式)方程组是电磁学实验规律的全面总结和高度概括被誉为电磁学中的牛顿定律14(简易的表述形式)qdsD-EldLmdtdF电场高斯定理环路定理电荷总伴随有电场变化磁场一定伴随有电场感应电场线是无头无尾的SisBds0磁场高斯定理环路定理磁场是无源场变化电场一定伴随有磁场磁力场线是无头无尾的Hld+ILDdtdFSics理解麦克斯韦方程组15理解麦克斯韦方程组揭示了电磁场的统一性和相对性空间带电体对相对其静止的观察者—静电场对相对其运动的观察者电场电磁波可脱离电荷、电流在空间传播麦克斯韦于1862年预言电磁波的存在能推断和解释一切电磁现象，且逻辑体系严密、数学形式简洁它完整地反映和概括了电磁场的运动规律16理解麦克斯韦方程组电磁波的传播速率真空中u1me000318ms真空中光速c它预言了光的电磁本性，将光学和电磁学统一起来电磁场是最简单的规范场，蕴藏着完美的对称结构——电磁对称它在技术上的应用促进了电子技术和生产力的高速发展近代一切电报、无线电、雷达、电视、计算机等……麦克斯韦方程的应用而已爱因斯坦评价说:“这个理论是以场为基本量的革命性的理论”.17简单、对称、和谐、统一理解麦克斯韦方程组麦克斯韦方程组是符合这些审美准则的典范DrB0tBeeEH+JtDee我们能够欣赏麦克斯韦方程中的美，也就懂得它蕴含的物理意义我们只有懂得麦克斯韦方程所蕴含的物理意义，才能欣赏它的美原天地之美，而达万物之理——庄子18DH+++++tVk2求两极板间的IDjD、HB、分布已知极板半径R电容CVtk2电源电压真空0mldlHdss两极板间jDIDFDdtdtdd((dtdqCVCtdd(tk2(Ctk2IDSpR2Ctk2jDp2Hrpr2H2rrpR2CtkB0mH0mrpR2CtkjDjD例19位移电流tdIDFDdDe0E2FDSDDpRpR2e0EIDFDdtdpR2e0Edtd已知：Re0D空气电容器Edtde0R,,例求：ID位移电流例20接高压电源振荡火花诱发火花赫兹(1857-1894)25年后,赫兹于1887年首次从实验中获得了电磁波.将感应线圈电极产发射:带有筒球和锌板的生的振荡高压,接至接收:弯成圆弧形的铜线两端接有铜球,调节铜球间的距离,能产生诱发火花,表明接收到电磁波.产生振荡火花,发射电磁波.导体棒,两铜球之间五、电磁波21从LC振荡电路到振荡电偶极子1.电磁波的产生~振荡电路LCLC激励源~激励源振荡电路LC半开放式~激励源振荡电路LC开放式~激励源振荡电偶极子22E与H平面EH+~+~极轴在子午面(一系列包含极轴的平面)内.E在与赤道面平行的平面内.H振荡电偶极子发射的电磁波23传播方向rEH振荡电偶极子发射的电磁波在子午面(一系列包含极轴的平面)内.E在与赤道面平行的平面内.H传播方向沿的方向.rEH与相互垂直.EH波场中任一点的+~+~极轴OEEHHO+~rr+~24接收1该接收天线与E平行时,.eilEdl的绝对值最大该接收天线与E垂直时,.eilEdl的绝对值最小用直线天线接收E波E超高頻发射天线25接收2接收线圈的法线与穿过线的绝对值最小sdtdBdsi接收线圈的法线与穿过线的绝对值最大sdtdBdsi用环形天线接收H波超高頻发射天线H26平面电磁波~+波源远离波源处的波面近似于平面E电振动磁振动HrEH、相互垂直，且都垂直于传播方向。EH、u、且构成右旋直角坐标。三者相互垂直，u方向传播HE沿2.平面电磁波27平面电磁波方程EruH介质em,电振幅OEH0磁振幅E.cosw()turE0HH0cosw()tur电波方程磁波方程同频率同相位EH、，28EruH介质em,电振幅OEH0磁振幅磁场能量密度电场能量密度21mH221HBwmmHBeED21eE221EDwe电磁波中的wewmeE2mH2有即eEmHeEmH00平面电磁波的振幅29电磁波的波速波速取决于媒质的物理性质em若,给定理论和实验都能证明波速ume1真空中u1me008.854011212.56601710318ms等于真空中光速c303.电磁波的基本性质eEmH00同频率同相位EH、，着重三点:且都EHu构成右旋直角坐标E、H、uu1me31电磁波的波强波强I21EH00单位：W.m-2电磁波强的内涵是平均能流密度ESuH介质em,电振幅OEH0磁振幅电磁波的能流密度swuEHEHs坡印廷矢量sIsT10Tdts21EH0032电磁波谱红外线紫外线微波无线电波X射线g射线可见光波长:1041810610210101012101104102410m1041810610210101011610104210281100210频率:Hz33emE0H0由对真空有：H0E0e0m08.8510124p1075001.33Am1cos2pn((txcHy1.33得Am1EzcH真空OEH0xym0Hm14p107e08.851012Fm1Ex500(SI)cos2pn((txc已知