中考数学与相似有关的压轴题及答案

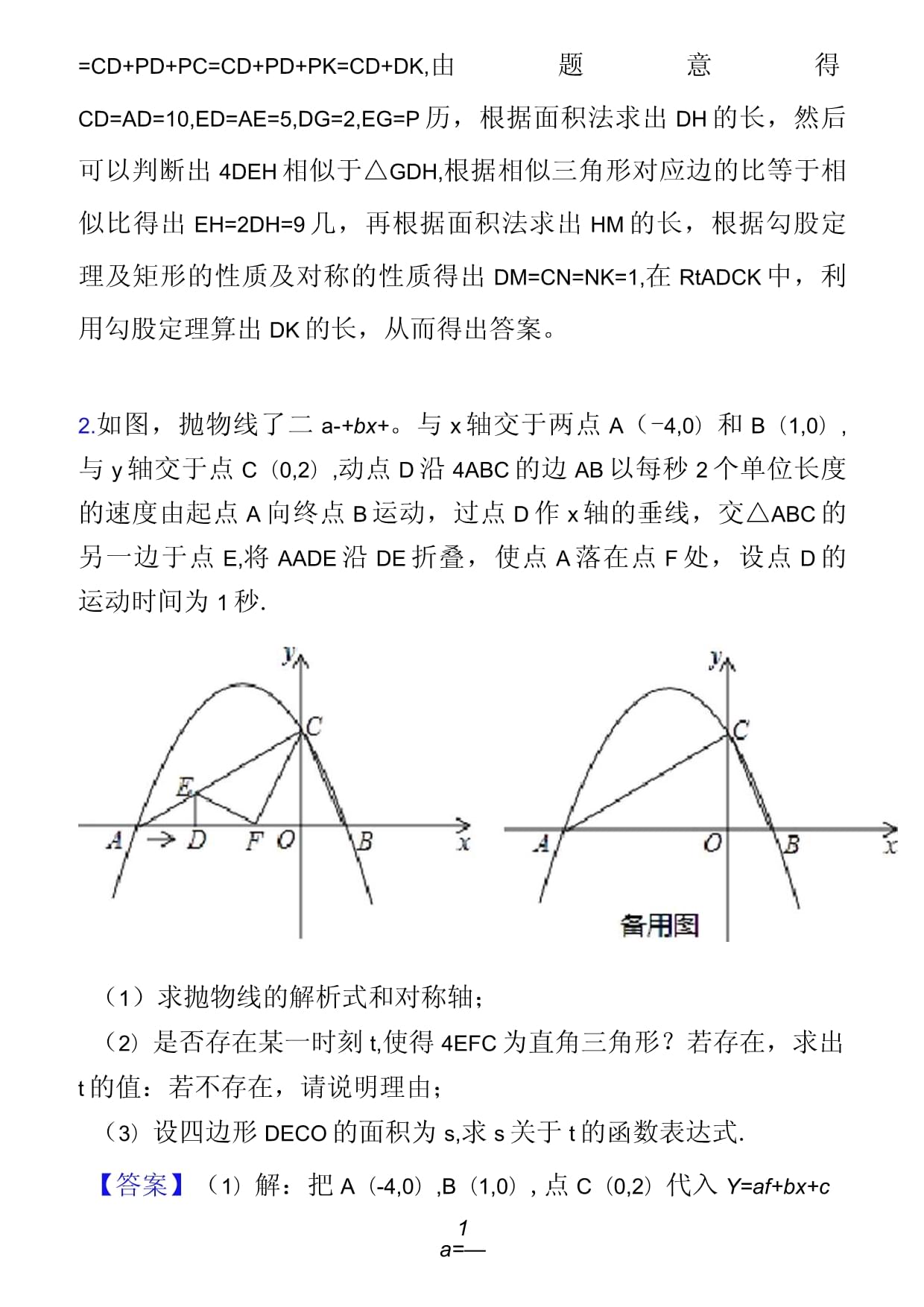
中考数学与相似有关的压轴题及答案一、相似1.如图，在正方形ABCD中，点E,F分别是边AD,BC的中点，连接DF,过点E作EHJLDF,垂足为H,EH的延长线交DC于点G.（1）猜想DG与CF的数量关系，并证明你的结论：（2）过点H作MNIICD,分别交AD,BC于点M,N,若正方形ABCD的边长为10,点P是MN上一点，求^PDC周长的最小值.【答案】（1）解：结论：CF=2DG.理由：四边形ABCD是正方形，•.AD=BC=CD=AB,ZADC=ZC=90%DE=AE,•.AD=CD=2DE,EGJLDF,•・ZDHG=90°,•・ZCDF+ZDGE=90%ZDGE+ZDEG=90。，•・ZCDF=ZDEG,DEG~△CDF,DGDE1d=应=2,「•CF=2DG（2）解：作点C关于NM的对称点K,连接DK交MN于点P,连接PC,此时△PDC的周长最短.周长的最小值=CD+PD+PC=CD+PD+PK=CD+DK.55ntDE♦DG由题意：CD=AD=10,ED=AE=5,DG=2,EG=2,DH=EG=、氏・•.EH=2DH=2DH•Eh/.HM=DE=2,/.DM=CN=NK='加一如=1,在RtADCK中,DK=+决=+汽府+（部产=2他,PCD的周长的最小值为10+2他.【解析】【分析】（1）结论：CF=2DG.理由如下：根据正方形的性质得出AD=BC=CD=AB,ZADC=ZC=90%根据中点的定义得出AD=CD=2DE,根据同角的余角相等得出NCDF=NDEG,从而判断出△DEG~△CDF,根据相似三角形对应边的比等于相似比即可得出结论；（2）作点C关于NM的对称点K,连接DK交MN于点P,连接PC,此时△PDC的周长最5短.周长的最小值=CD+PD+PC=CD+PD+PK=CD+DK,由题意得CD=AD=10,ED=AE=5,DG=2,EG=P历，根据面积法求出DH的长，然后可以判断出4DEH相似于△GDH,根据相似三角形对应边的比等于相似比得出EH=2DH=9几，再根据面积法求出HM的长，根据勾股定理及矩形的性质及对称的性质得出DM=CN=NK=1,在RtADCK中，利用勾股定理算出DK的长，从而得出答案。2.如图，抛物线了二a-+bx+。与x轴交于两点A（-4,0）和B（1,0）,与y轴交于点C（0,2）,动点D沿4ABC的边AB以每秒2个单位长度的速度由起点A向终点B运动，过点D作x轴的垂线，交△ABC的另一边于点E,将AADE沿DE折叠，使点A落在点F处，设点D的运动时间为1秒.（1）求抛物线的解析式和对称轴；（2）是否存在某一时刻t,使得4EFC为直角三角形？若存在，求出t的值：若不存在，请说明理由；（3）设四边形DECO的面积为s,求s关于t的函数表达式.【答案】（1）解：把A（-4,0）,B（1,0）,点C（0,2）代入Y=af+bx+c1

a=—2TOC\o"1-5"\h\z16a-4b+c=01二」{a+b+c=02得：c=2,解得：c二2,L3.Y产X+2••・抛物线的解析式为：.22,3对称轴为：直线x=-2：(2)解：存在,•/AD=2t,・・・DF=AD=2t,・•・0F=4-43・・・D(2t-4,0),1v=-x2二直线AC的解析式为：,2,.・.E(2t-4,t),.「△EFC为直角三角形，分三种情况讨论：①当/EFC=90°,则4DEF-△OFC,DEDFt2t3.•.苏一五，即4-41-7,解得：t=)：②当/FEC=90%・•.ZAEF=90%AEF是等腰直角三角形，・・.DE=2aF,即t=2t,/.t=0,(舍去)，<5③当NACF=90。，则AC2+CF2=AF2,即(42+22)+[22+(4t-4)2]=(4t)2,解得：t=4,35・・・存在某一时刻t,使得4EFC为直角三角形，此时，或；；(3)解：:B(1,0),C(0,2),「•直线BC的解析式为：y=-2x+2,11当D在y轴的左侧时，S=2(DE+OC)・OD=2(t+2)•(4-2t)=-t2+4(0<t<2)；当D在y轴的右侧时，如图2,

OD=4t-4,DE=-8t+10,S=W(DE+OC)55--16T2+40t-24(2<t<2).-t24(0<t<2)1•0D=2(-1•0D=2(-8t+10+2)•(4t-4),即S={综上所述：

【解析】【分析】-16V+40t-24(2<t<（I）（1）利用待定系数法，将点A、B、C的坐标代入函数解析式，建立方程组求解即可。（2）根据题意分别求出AD、DF、OF的长，表示出点D的坐标，利用待定系数法求出直线BC的函数解析式，表示出点E的坐标，再分三种情况讨论△EFC为直角三角形：①当NEFC=90。，则△DEF~AOFC,根据相似三角形的性质，列出关于t的方程求解即可；②NFEC=90。，NAEF=90。，△AEF是等腰直角三角形求出t的值即可；③当NACF=90。，则AC2+CF2=AF2,建立关于t的方程求解即可，从而可得出答案。（3）求得直线BC的解析式为：y=-2x+2,当D在y轴的左侧时，当D在y轴的右侧时，如图2,根据梯形的面积公式即可得到结论。3.如图①，已知直线11Hl2，线段AB在直线I1上，BC垂直于I1交I2于点C,且AB=BC,P是线段BC上异于两端点的一点，过点P的直线分别交b，li于点D,E（点A,E位于点B的两侧,满足BP=BE,连接AP,CE.①②（1）求证：△ABP2△CBE.（2）连接AD、BD,BD与AP相交于点F,如图②.BC_①当分时，求证：AP±BD；BCSi--73一②当6尸（n>l）时，设4PAD的面积为Si,4PCE的面积为S2,求&的值.【答案】（1）证明：BC，直线h,ZABP=ZCBE.在^ABP和^CBE中，AB=CBf{ZABP=NCBE,BP=BE,（2）①证明：如图，延长AP交CE于点H.•：匕ABP登△CBE,ZPAB=ZECB,「・ZPAB+ZAEH=ZECB+ZAEH=90°,/.ZAHE=90°,AP±CE.BC_•••而一"，即P为BC的中点，直线I】II直线I，「・△CPD〜△BPE,DPCP----1「・EPBP,「•DP=EP.••・四边形BDCE是平行四边形，CEIIBD.AP±CE,/.AP±BD.BC--n②解：:BP，,BC=nBP,「•CP=(n-l)BP.CDIIBE,・•.△CPD~△BPE,PDPC----7?~/・•・PEPB令Sabpe=S,则S2=(n—1)S,SaPAB=S△BCE=nSfSaPAE=(n+l)S・s△PADPD-=n-1■:S△paePE,「・Si=(n+l)(n-l)S,Si（n+1）（n-1）S-=n+1S2（n-1）S.【解析】【分析】（1）由己知条件用边角边即可证得△ABP登△CBE；（2）①、延长AP交CE于点H,由（1）知^ABP2△CBE,所以可得NPAB=ZECB,而NNECB+NBEC=9。'，所以可得NPAB+NBEC=90'，即NAHE=90'，所以AP_LCE：己知BC面=2,则点P为BC的中点，所以易证得BE=CD,由有一组对边平行且相等的四边形是平行四边形可得四边形BDCE是平行四边形，由平行四边形的性质可得CEIIBD,再根据平行线的性质即可求得AP_LBD；②方法与①类似，由己知条件易证得△CPD~aBPE,则可得对应线段的比相等，然后可将APAD的面积和APCE的面枳用三角形BPE的面积表示出来，则这两个三角形的比值即可求解。4.如图1,以ejABCD的较短边CD为一边作菱形CDEF,使点F落在边AD上，连接BE,交AF于点G.图1图2图3（1）猜想BG与EG的数量关系.并说明理由;（2）延长DE,BA交于点H,其他条件不变，DG①如图2,若NADC=60。，求班的值；DG②如图3,若NADC=a（0。。＜90。），直接写出原的值.（用含a的三角函数表示）【答案】（1）解：BG二EG,理由如下：・「四边形月箭是平行四边形，Ab||CLyAB=CD,・「四边形侬7是菱形，/.夕II/，CD=EF.Ab||EF,AB=EF.NABG=NFEG.又/ZAGB=ZFGE,・.AABG^AFEG（幽5）.・・BG=EG(2)解：方法1：过点6作⑶II应，交〃族于点心,.・.NEMG=NEHA./NGEM=ZBEh,・・/腹〜ABHL.GM_GE而一瓦.由（1）结论知3G=EG,1EG=-BE•9••~•GMGE_1・・茄一应一，.••四边形四济为菱形，・.ZADC=NEDF=60：「四边形，始Q是平行四边形，Ab||CL.・・NCDF=/HAD=60°•••/翁||Ah,JNMGD=NHAD=60°・••・・・ZGMD=1800-ZMGD-ZMDG=60°,即ZGMD=ZMGD=ZMGD=60°.”是等边三角形。/.DG=MG.DGMG_1・・・那―第一方法2：延长以，戊交于点心，II・・・四边形如为菱形，ZEDF=NCDF=60：四边形,四口为平形四边形，ZABC=ZADC=60°,AL||BC..・.NEDF==60Q.ZH=180°-ZHBM-=180°-60°=60即/HBM==ZH=60°./阳》为等边三角形./.HB二阪'：AL||BC,/.NEGD=NEBA,NEDG=Zk.AEDG〜^EMb,DG_EG届一届.由⑴结论知3G=EG1EG=-BE：.2.DGGE_1•/HB=MBfDGDG_1「•茄一砺一；.如图3,连接EC交DF于0,・・・四边形CFED是菱形,・•.EC±AD,FD=2F0,设FG=a,AB=b,则FG=a,EF=ED=CD=b,OhRtAEFO中，cosa=EF,OF=bcosa,DG=a+2bcosa,过H作HM±AD于M,•/ZADC=ZHAD=ZADH=a,/.AH=HD,11/.AM=-AD=-(2a+2bcosa)=a+bcosa,/iRtAAHM中，cosa二也，a+bcoso：.AH=cosa,a+2Aos〃DGa+bcosa-b+/.Bh=cos"=cosa【解析】【分析】(1)利用菱形和平行四边形的性质可得出ABIICDIIEF,AB=CD=EF,再利用平行线的性质可证得NABG=NFEG,然后利用AAS可证得△ABG2△FEG,由全等三角形的性质可证得结论。(2)①过点G作GMIIBH,交DH于点M,易证△GME~△BHE。得出对应边成比例，求出MG与BH的比值，再利用菱形的性质及平行四边形的性质证明DG=MG,即可解答；②连接EC交DF于0,利用菱形的性质可得出EC_LAD,FD=2F0,设FG=a,AB=b,可表示出FG,EF=ED=CD=b,RtAEFO中，利用锐角三角函数的定义可得出OF、DG,过H作HM_LAD于M,易证AH=HD,AM=a+bcosa,再在R3AHM中，利用锐角三角函数的定义求出AH的长，继而可得出DG与BH的比值，可解答。5.如图，△ABC内接于OO,ZCBG=ZA,CD为直径，0C与AB相交于点E,过点E作EF±BC,垂足为F,延长CD交GB的延长线于点P,连接BD.(1)求证：PG与。0相切；Ek5BE(2)若五二，求五的值；(3)在(2)的条件下，若。0的半径为8,PD=OD,求0E的长.【答案】（1）解：如图，连接0B,则OB=OD,•・ZBDC=ZDBO,/ZBAC=ZBDC、ZBAC=ZGBC,•・ZGBC=ZBDO,CD是OO的直径，•.ZDBO+ZOBC=90°,「•ZGBC+ZOBC=90°,•.ZGBO=90°,/.PG与。0相切。（2）解：过点。作OMJLAC于点M,连接OA,1则NAOM=ZCOM=2ZAOC,圆心角/ABC和圆周痛/AOC所对弧相同，、1•.ZABC=Z/aoc=zcom,又「ZEFB=ZOMC=90°,△BEF~△OCM,EFBEJ•・•CM=2AC,EF_Bb厂一区-AC：.2,EF_5又fAC~~8,BEEF55—=2X—=2BE5（3）解：由（2）可知窕=4,则BE=10.・•PD=OD,ZPBO=90°,「・BD=0D=8,在RtADBC中，BC=个Dd-B抉=8W,又「OD=OB,…DOB是等边三角形，•・ZDOB=60%/ZDOB=ZOBC+ZOCB,OB=OC,•・ZOCB=30°,EF_1FC「•日一£,百二、Z3,••可设EF=x,则EC=2x、FC=/x,•・BF=8/-Wx,在RtABEF中，BE2=EF2+BF2,•・100=x2+（8/-Wx）2,解得：x=6±\.^,6+V^>8,舍去，x=6-,•・EC=12-2",/.0E=8-（12-2%历）=2%历-4【解析】【分析】（1）连接OB,则需要证明NGBO=NGBC+NOBC=90°；由CD是。0的直径，则NDBO+NOBC=90。，即需要证明NGBC=NBDO,由同弧所对的圆周角相等，可知ZBAC=ZBDC,而NBAC=ZGBC,ZBDC=ZDBO,则可证得NGBC=ZBDOoEF5Bh（2）因为己知水=8,求窕，其中EF,BE是^BEF的两条边，而AC,0C是△AOC的两条边，但△BEF和△AOC不相似，则可构造两三角形相似，因为△BEF是直角三角形，则可过Bh点。作OM_LAC于点M,连接OA,即构造△BEF~△OCM,从而可求得窕。BE（3）由（2）得窕的值及0C=8求出BE；由PD=OD,且NPBO=90。，根据“直角三角形斜边上的中线长等于斜边长的一半"可得BD=OD=8,由勾股定理可求得BC的长，MaDOB是等边三角形，则在直角三角形ECF中存在特殊角30度，不妨设EF=x,则CE=2x,CF八每。在RSBEF中，由勾股定理可得BE?=EF2+BF2,构造方程解答即可。6.若一个三角形一条边的平方等于另两条边的乘积，我们把这个三角形叫做比例三角形.

AA(1)已知△ABC是比例三角形，AB=2,BC=3.请直接写出所有满足条件的AC的长；(2)如图1,在四边形ABCD中，ADIIBC,对角线BD平分NABC,ZBAC=ZADC.求证：△ABC是比例三角形；BL(3)如图2,在(2)的条件下,当NADC=90。时，求水的值。46【答案】(1)3或2或筐.(2)证明：•••ADIIBC,•・ZACB=ZCAD,又「ZBAC=ZADC,「・△ABC〜△DCA,BCCA：.CA=AL,即CA2=BC-AD,ADIIBC,•・ZADB=ZCBD,/BD平分NABC,•・ZABD=ZCBD,•・ZADB=ZABD,「•AB=AD,「•CA2=BC-AB,・・aABC是比例三角形.（3）解：如图，过点A作AHJLBD于点H,BH=/BD,.ADIIBC,ZADC=90°/ZBHA=ZBCD=90°,又「ZABH=ZDBC,△ABH-△DBQABBh：.~Db=~BCf・•・AB・BC=DB-BH,1「•AB・BC=2BD2,又「AB-BC=AC2Zbd2=ac2zBL五=遂.【解析】【解答】解：⑴.••己知△ABC是比例三角形，依题可得：①当AB2=BC-AC时，VAB=2,BC=3./.4=3AC,4：.AC=5；②CB2=AB-AC,・「AB=2,BC=3.「♦9=2AC,g/.AC=2；③AC?=BC・AB,・「AB=2,BC=3.「•AC2=2x3,/.AC=#.4g综上所述：AC的长为：彳或；或筐.【分析】（1）由比例三角形的定义分三种情况讨论:①当AB2=BCAC时,②CB2=ABAC,（3）AC2=BC-AB,代入CB、AB的数值分别求得AC长.（2）根据平行线的性质和相似三角形的判定得△ABC~△DCA,由相似三角形的性质得CA2=BC-AD；根据平行线的性质和角平分线的定义得NADBNABD,根据等腰三角形等角对等边得AB=AD,将此代入上式即可得证.（3）如图，过点A作AH±BD于点H,根据等腰三角形三线合一的性质可知BH=；BD,由相似三角形的判定和性质得ABBC=DB-BH,即ABBC=2BD?,联立（1）中的结论即可得出答案.7.如图，抛物线丫=ax?+bx-4经过AV-3,①，B⑶-4两点，与y轴交于点C,连接AB,AC,BC.(1)求抛物线的表达式；(2)求证：AB平分4A0；(3)抛物线的对称轴上是否存在点M,使得4ABM是以AB为直角边的直角三角形，若存在，求出点M的坐标；若不存在，请说明理由.,%一氏-4二0【答案】(1)解：将—B⑶一夕代入得：125a十氏-4二-4,TOC\o"1-5"\h\z15a--b--解得：6,6,125

y二一X乙一""X-4:抛物线的解析式为.66（2）解：⑵：•A0=3,0C=4,•:AC=3,取D色切，则AD=AC=5,（-（-4-0）2=5y•・•C（a-4）,B⑸-4）,:BC=5,:BD=BC,在ABC和4ABD中，AD=AC,AB-AB,BD=BC,,ABC2Z\ABD,:"AB=4AD,:AB平分NtAO（3）解：如图所示：抛物线的对称轴交x轴与点E,交BC与点F.•:tan-ZEAB--2,：•Tab二,:tanNM'AE=2,:M'E二舜二11,5:M'(-11)2,同理：tan^IMF=2,:FM=5,5:M弓-9）55―9）•:点M的坐标为2或2【解析】【分析】（1）利用待定系数法，将点A、B两点坐标分别代入抛物线的解析式，求出a、b的值，即可解答。（2）利用勾股定理，在RtAAOC中，求出AC的长，再根据两点间的距离公式求出BD的长，由点B、C的坐标，求出BC的长，可证得BD=BC,然后证明^ABC△ABD,利用全等三角形的性质，可证得结论。（3）抛物线的对称轴交x轴与点E,交BC与点F.求出抛物线的对称轴，就可求出AE的长，再利用点A、B的坐标，求出tanZEAB的值，再由NM'AB=90。，求出tanZZM'AE

的值，求出M，E的长，就可得出点M’的坐标，再用同样的方法求出点M的坐标，即可解答。\fTccosB8.如图：在0c中，BC=2ZAB=AC,点D为AC上的动点，且.(1)求AB的长度；(2)求ADAE的值；(3)过A点作AH_LBD,求证：BH=CD+DH.【答案】(1)解：作AM_LBC,J.BM=CM=2BC=1Z在RtAAMB中，BM、伉——cosB=10y[ld•・AB=BM+cosB=1+10=木乙(2)解：连接CD,AB=AC,•・ZACB=ZABC,丁四边形ABCD内接于圆0,「•ZADC+ZABC=180°,又「ZACE+ZACB=180°,ZADC=ZACE,/ZCAE=ZCAD,•・△EAJ△CAD,AC_AE：.~AD~~ACf/.AD-AE=AC2=AB2=(«n)2=10.(3)证明：在BD上取一点N,使得BN=CD,ABN和^ACD中AB=AC{N3=Z1/BN二CD「•△ABN^△ACD（SAS）,「•AN=AD,AH±BD>AN=AD,「•NH=DH,又「BN=CD,NH=DH,BH=BN+NH=CD+DH.1【解析】【分析】（1）作AM_LBC,由等腰三角形三线合一的性质得BM=CM=；BC=1,在BM_yflGRtAAMB中，根据余弦定义得cosB=AB10，由此求出AB.（2）连接CD,根据等腰三角形性质等边对等角得NACB=NABC,再由圆内接四边形性质和等角的补角相等得NADC=NACE；由相似三角形的判定得△EAC~△CAD,根据相似三角形的性质得AC_AE1—1Q月c；从而得ad-ae=ac2=ab2.（3）在BD上取一点N,使得BN=CD,根据SAS得公ABN2△ACD,再由全等三角形的性质得AN=AD,根据等腰三角形三线合一的性质得NH=DH,从而得BH=BN+NH=CD+DH.9.如图，在平面直角坐标系中，已知抛物线y=2x2+*x-2与x轴交于A,B两点（点A在点B的左侧），与y轴交于点C,直线I经过A,C两点，连接BC.（1）求直线I的解析式