2023届山东省东营市胜利第二中学九年级数学第一学期期末达标测试试题含解析

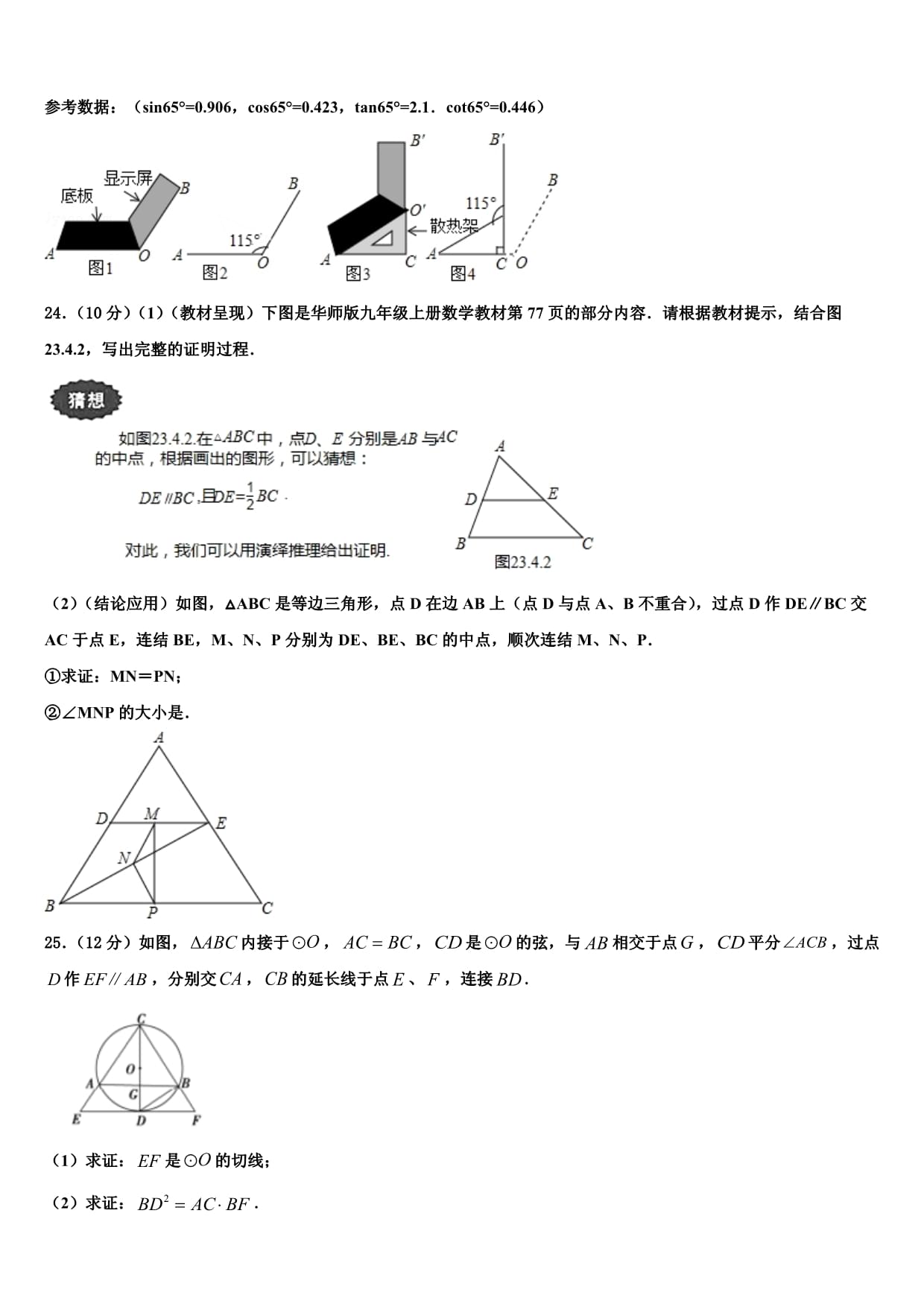
2022-2023学年九上数学期末模拟试卷注意事项1．考试结束后，请将本试卷和答题卡一并交回．2．答题前，请务必将自己的姓名、准考证号用0．5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置．3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符．4．作答选择题，必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑；如需改动，请用橡皮擦干净后，再选涂其他答案．作答非选择题，必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效．5．如需作图，须用2B铅笔绘、写清楚，线条、符号等须加黑、加粗．一、选择题（每题4分，共48分）1．下列说法正确的是（）A．25人中至少有3人的出生月份相同B．任意抛掷一枚均匀的1元硬币，若上一次正面朝上，则下一次一定反面朝上C．天气预报说明天降雨的概率为10%，则明天一定是晴天D．任意抛掷一枚均匀的骰子，掷出的点数小于3的概率是2．计算得（）A．1 B．﹣1 C． D．3．主视图、左视图、俯视图分别为下列三个图形的物体是（）A． B． C． D．4．如图，菱形ABCD的两条对角线AC，BD相交于点O，E是AB的中点，若AC＝6，BD＝8，则OE长为（）A．3 B．5 C．2.5 D．45．如图是二次函数y=ax1+bx+c（a≠0）图象的一部分，对称轴是直线x=﹣1．关于下列结论：①ab<0；②b1﹣4ac>0；③9a﹣3b+c>0；④b﹣4a=0；⑤方程ax1+bx=0的两个根为x1=0，x1=﹣4，其中正确的结论有（）A．②③ B．②③④ C．②③⑤ D．②③④⑤6．不透明的袋子中装有形状、大小、质地完全相同的6个球，其中4个黑球、2个白球，从袋子中一次摸出3个球，下列事件是不可能事件的是（）A．摸出的是3个白球 B．摸出的是3个黑球C．摸出的是2个白球、1个黑球 D．摸出的是2个黑球、1个白球7．如图，矩形AOBC，点C在反比例的图象上，若，则的长是（）A．1 B．2 C．3 D．48．二次函数的顶点坐标为（）A． B． C． D．9．已知关于x的一元二次方程xaxb0ab的两个根为x1、x2，x1x2则实数a、b、x1、x2的大小关系为（）A．ax1bx2 B．ax1x2b C．x1ax2b D．x1abx210．能判断一个平行四边形是矩形的条件是（）A．两条对角线互相平分 B．一组邻边相等C．两条对角线互相垂直 D．两条对角线相等11．的半径为5，圆心O到直线l的距离为3，则直线l与的位置关系是A．相交 B．相切 C．相离 D．无法确定12．在平面直角坐标系中，二次函数的图像向右平移2个单位后的函数为()A． B．C． D．二、填空题（每题4分，共24分）13．某学校的初三（1）班，有男生20人，女生23人．现随机抽一名学生，则：抽到一名男生的概率是_____．14．已知，则的值是_______．15．正五边形的中心角的度数是_____．16．如图，用一张半径为10cm的扇形纸板做一个圆锥形帽子（接缝忽略不计），如果做成的圆锥形帽子的高为8cm，那么这张扇形纸板的弧长是________cm．17．已知2是关于的一元二次方程的一个根，则该方程的另一个根是________．18．如图，把△ABC绕点C按顺时针方向旋转35°，得到△A’B’C，A’B’交AC于点D，若∠A’DC=90°，则∠A=°.三、解答题（共78分）19．（8分）小红想利用阳光下的影长测量学校旗杆AB的高度．如图，她在地面上竖直立一根2米长的标杆CD，某一时刻测得其影长DE＝1.2米，此时旗杆AB在阳光下的投影BF＝4.8米，AB⊥BD，CD⊥BD．请你根据相关信息，求旗杆AB的高．20．（8分）解方程：（1）x2﹣2x﹣1＝0；（2）（2x﹣1）2＝4（2x﹣1）．21．（8分）如图，在Rt△ABC中，∠C=90°，以BC为直径的⊙O交斜边AB于点M，若H是AC的中点，连接MH．（1）求证：MH为⊙O的切线．（2）若MH=，tan∠ABC=，求⊙O的半径．（3）在（2）的条件下分别过点A、B作⊙O的切线，两切线交于点D，AD与⊙O相切于N点，过N点作NQ⊥BC，垂足为E，且交⊙O于Q点，求线段NQ的长度．22．（10分）如图，在平面直角坐标系中，将一个图形绕原点顺时针方向旋转称为一次“直角旋转，已知的三个顶点的坐标分别为，，，完成下列任务：（1）画出经过一次直角旋转后得到的；（2）若点是内部的任意一点，将连续做次“直角旋转”（为正整数），点的对应点的坐标为，则的最小值为；此时，与的位置关系为．(3)求出点旋转到点所经过的路径长．23．（10分）将笔记本电脑放置在水平桌面上，显示屏OB与底板OA夹角为115°（如图1），侧面示意图为图2；使用时为了散热，在底板下面垫入散热架O′AC后，电脑转到AO′B′的位置（如图3），侧面示意图为图4，已知OA=OB=20cm，B′O′⊥OA，垂足为C．（1）求点O′的高度O′C；（精确到0.1cm）（2）显示屏的顶部B′比原来升高了多少？（精确到0.1cm）（3）如图4，要使显示屏O′B′与原来的位置OB平行，显示屏O′B′应绕点O′按顺时针方向旋转多少度？参考数据：（sin65°=0.906，cos65°=0.423，tan65°=2.1．cot65°=0.446）24．（10分）（1）（教材呈现）下图是华师版九年级上册数学教材第77页的部分内容．请根据教材提示，结合图23.4.2，写出完整的证明过程．（2）（结论应用）如图，△ABC是等边三角形，点D在边AB上（点D与点A、B不重合），过点D作DE∥BC交AC于点E，连结BE，M、N、P分别为DE、BE、BC的中点，顺次连结M、N、P．①求证：MN＝PN；②∠MNP的大小是．25．（12分）如图，内接于，，是的弦，与相交于点，平分，过点作，分别交，的延长线于点、，连接.（1）求证：是的切线；（2）求证：.26．（1）2y2+4y＝y+2（用因式分解法）（2）x2﹣7x﹣18＝0（用公式法）（3）4x2﹣8x﹣3＝0（用配方法）

参考答案一、选择题（每题4分，共48分）1、A【分析】根据概率的意义对各选项分析判断后利用排除法求解．【详解】A、25人中至少有3人的出生月份相同，原说法正确，故这个选项符合题意；B、任意抛掷一枚均匀的1元硬币，若上一次正面朝上，则下一次可能正面朝上，可能反面朝上，原说法错误，故这个选项不符合题意；C、天气预报说明天的降水概率为10%，则明天不一定是晴天，原说法错误，故这个选项不符合题意；D、任意抛掷一枚均匀的骰子，掷出的点数小于3有2种可能，故概率是，原说法错误，故这个选项不符合题意；故选：A．【点睛】本题考查了概率的意义，概率是反映事件发生机会的大小的概念，只是表示发生的机会的大小，机会大也不一定发生，机会小也有可能发生．2、A【分析】根据题意对原式变形后，利用同分母分式的减法法则计算，约分即可得到结果．【详解】解：=1．故选：A．【点睛】本题考查分式的加减法，熟练掌握分式的加减法运算法则是解答本题的关键．3、A【解析】分析：本题时给出三视图，利用空间想象力得出立体图形，可以先从主视图进行排除.解析：通过给出的主视图，只有A选项符合条件.故选A.4、C【分析】根据菱形的性质可得OB=OD，AO⊥BO，从而可判断OE是△DAB的中位线，在Rt△AOB中求出AB，继而可得出OE的长度．【详解】解：∵四边形ABCD是菱形，AC=6，BD=8，

∴AO=OC=3，OB=OD=4，AO⊥BO，

又∵点E是AB中点，

∴OE是△DAB的中位线，

在Rt△AOD中，AB==5，

则OE=AD=．

故选C．【点睛】本题考查了菱形的性质及三角形的中位线定理，熟练掌握菱形四边相等、对角线互相垂直且平分的性质是解题关键．5、D【分析】根据二次函数的图像与性质即可得出答案.【详解】由图像可知，a＜0，b＜0，故①错误；∵图像与x轴有两个交点∴，故②正确；当x=-3时，y=9a﹣3b+c，在x轴的上方∴y=9a﹣3b+c>0，故③正确；∵对称轴∴b-4a=0，故④正确；由图像可知，方程ax1+bx=0的两个根为x1=0，x1=﹣4，故⑤正确；故答案选择D.【点睛】本题考查的是二次函数的图像与性质，难度系数中等，解题关键是根据图像判断出a，b和c的值或者取值范围.6、A【解析】由题意可知，不透明的袋子中总共有2个白球，从袋子中一次摸出3个球都是白球是不可能事件，故选B.7、B【分析】根据OB的长度即为点C的横坐标，代入反比例函数的解析式中即可求出点C的纵坐标，即BC的长度，再根据矩形的性质即可求出OA．【详解】解：∵∴点C的横坐标为1将点C的横坐标代入中，解得y=2∴BC=2∵四边形AOBC是矩形∴OA=BC=2故选B．【点睛】此题考查的是根据反比例函数解析式求点的坐标和矩形的性质，掌握根据反比例函数解析式求点的坐标和矩形的性质是解决此题的关键．8、D【分析】已知二次函数y＝2x2＋3为抛物线的顶点式，根据顶点式的坐标特点直接写出顶点坐标．【详解】∵y＝2x2＋3＝2（x−0）2＋3，∴顶点坐标为（0，3）．故选：D．【点睛】本题考查了二次函数的性质：二次函数的图象为抛物线，则解析式为y＝a（x−k）2＋h的顶点坐标为（k，h），9、D【分析】根据二次函数的图象与性质即可求出答案．【详解】如图，设函数y＝（x−a）（x−b），当y＝0时，x＝a或x＝b，当y＝时，由题意可知：（x−a）（x−b）−＝0（a＜b）的两个根为x1、x2，由于抛物线开口向上，由抛物线的图象可知：x1＜a＜b＜x2故选：D．【点睛】本题考查一元二次方程，解题的关键是正确理解一元二次方程与二次函数之间的关系，本题属于中等题型．10、D【分析】根据矩形的判定进行分析即可；【详解】选项A中，两条对角线互相平分是平行四边形，故选项A错误；选项B中，一组邻边相等的平行四边形是菱形，故选项B错误；选项C中，两条对角线互相垂直的平行四边形是菱形，故选项C错误；选项D中，两条对角线相等的平行四边形是矩形，故选项D正确；故选D.【点睛】本题主要考查了矩形的判定，掌握矩形的判定是解题的关键.11、A【分析】根据直线和圆的位置关系可知，圆的半径大于直线到圆距离，则直线l与O的位置关系是相交．【详解】∵⊙O的半径为5，圆心O到直线的距离为3，∴直线l与⊙O的位置关系是相交．故选A．【点睛】本题考查了直线和圆的位置关系，直接根据直线和圆的位置关系解答即可．12、B【分析】根据“左加右减，上加下减”的规律，求出平移后的函数表达式即可；【详解】解：根据“左加右减，上加下减”得，二次函数的图像向右平移2个单位为：；故选B.【点睛】本题主要考查了二次函数与几何变换，掌握二次函数与几何变换是解题的关键.二、填空题（每题4分，共24分）13、【分析】随机抽取一名学生总共有20+23＝43种情况，其中是男生的有20种情况．利用概率公式进行求解即可．【详解】解：一共有20+23＝43人,即共有43种情况,∴抽到一名男生的概率是．【点睛】本题考查了用列举法求概率,属于简单题,熟悉概率的计算公式是解题关键.14、【分析】由可设a=k，b=3k，代入中即可.【详解】解：∵，∴设a=k，b=3k，代入中，==.故答案为：.【点睛】本题考查比例线段，解题的关键是学会利用参数解决问题，属于中考常考题型．15、72°．【分析】根据正多边形的圆心角定义可知：正n边形的圆中心角为，则代入求解即可．【详解】解：正五边形的中心角为：．故答案为72°．【点睛】此题考查了正多边形的中心角的知识．题目比较简单，注意熟记定义．16、【分析】首先求出圆锥的底面半径，然后可得底面周长，问题得解．【详解】解：∵扇形的半径为10cm，做成的圆锥形帽子的高为8cm，∴圆锥的底面半径为cm，∴底面周长为2π×6＝12πcm，即这张扇形纸板的弧长是12πcm，故答案为：12π．【点睛】本题考查圆锥的计算，用到的知识点为：圆锥的底面周长＝侧面展开扇形的弧长．17、-1．【解析】设方程的另一个根为,由韦达定理可得:,即,解得.点睛:本题主要考查一元二次方程根与系数的关系,解决本题的关键是要熟练掌握一元二次方程根与系数的关系.18、55.【详解】试题分析：∵把△ABC绕点C按顺时针方向旋转35°，得到△A’B’C∴∠ACA’=35°，∠A=∠A’，.∵∠A’DC=90°，∴∠A’=55°.∴∠A=55°.考点：1.旋转的性质；2.直角三角形两锐角的关系.三、解答题（共78分）19、旗杆AB的高为8m．【分析】证明△ABF∽△CDE，然后利用相似比计算AB的长．【详解】∵AB⊥BD，CD⊥BD，∴∠AFB＝∠CED，而∠ABF＝∠CDE＝90°，∴△ABF∽△CDE，∴＝，即，∴AB＝8（m）．答：旗杆AB的高为8m．【点睛】本题考查了平行投影：由平行光线形成的投影是平行投影，如物体在太阳光的照射下形成的影子就是平行投影．平行投影中物体与投影面平行时的投影是全等的．20、（1）x＝2±；（2）x＝或x＝．【分析】（1）根据配方法即可求出答案．（2）根据因式分解法即可求出答案．【详解】解：（1）∵x2﹣2x﹣1＝0，∴x2﹣2x+1＝2，∴（x﹣2）2＝2，∴x＝2±．（2）∵（2x﹣1）2＝4（2x﹣1），∴（2x﹣1﹣4）（2x﹣1）＝0，∴x＝或x＝.【点睛】此题主要考查一元二次方程的求解，解题的关键是熟知一元二次方程的解法.21、（1）证明见解析；（2）2；（3）．【分析】（1）连接OH、OM，易证OH是△ABC的中位线，利用中位线的性质可证明△COH≌△MOH，所以∠HCO=∠HMO=90°，从而可知MH是⊙O的切线；（2）由切线长定理可知：MH=HC，再由点M是AC的中点可知AC=3，由tan∠ABC=，所以BC=4，从而可知⊙O的半径为2；（3）连接CN，AO，CN与AO相交于I，由AC、AN是⊙O的切线可知AO⊥CN，利用等面积可求出可求得CI的长度，设CE为x，然后利用勾股定理可求得CE的长度，利用垂径定理即可求得NQ．【详解】解：（1）连接OH、OM，∵H是AC的中点，O是BC的中点∴OH是△ABC的中位线∴OH∥AB，∴∠COH=∠ABC，∠MOH=∠OMB又∵OB=OM，∴∠OMB=∠MBO∴∠COH=∠MOH，在△COH与△MOH中，∵OC=OM，∠COH=∠MOH，OH=OH∴△COH≌△MOH（SAS）∴∠HCO=∠HMO=90°∴MH是⊙O的切线；（2）∵MH、AC是⊙O的切线∴HC=MH=∴AC=2HC=3∵tan∠ABC=，∴=∴BC=4∴⊙O的半径为2；（3）连接OA、CN、ON，OA与CN相交于点I∵AC与AN都是⊙O的切线∴AC=AN，AO平分∠CAD∴AO⊥CN∵AC=3，OC=2∴由勾股定理可求得：AO=∵AC•OC=AO•CI，∴CI=∴由垂径定理可求得：CN=设OE=x，由勾股定理可得：∴，∴x=，∴CE=，由勾股定理可求得：EN=，∴由垂径定理可知：NQ=2EN=．22、（1）图见解析；（2）2，关于中心对称；（3）．【分析】（1）根据图形旋转的性质画出旋转后的△即可；（2）根据中心对称的性质即可得出结论；（3）根据弧长公式求解即可．【详解】解：（1）如图，△即为所求；（2）点的对应点的坐标为，点与关于点对称，．故答案为：2，关于中心对称．（3）∵点A坐标为∴，则旋转到点所经过的路径长．【点睛】本题考查了根据旋转变换作图以及弧长公式，解答本题的关键是根据网格结构找出对应点的位置．23、（1）8.5cm；（2）显示屏的顶部B′比原来升高了10.3cm；（3）显示屏O′B′应绕点O′按顺时针方向旋转25度．【解析】（1）∵B′O′⊥OA，垂足为C，∠AO′B=115°，∴∠AO′C=65°，∵cos∠CO′A=，∴O′C=O′A•cos∠CO′A=20•cos65°=8.46≈8.5（cm）；（2）如图2，过B作BD⊥AO交AO的延长线于D．∵∠AOB=115°，∴∠BOD=65°．∵sin∠BOD=，∴BD=OB•sin∠BOD=20×sin65°=18.12，∴O′B′+O′C﹣BD=20+8.46﹣18.12=10.34≈10.3（cm），∴显示屏的顶部B′比原来升高了10.3cm；（3）如图4，过O′作EF∥OB交AC于E，∴∠FEA=∠BOA=115°，∠FOB′=∠EO′C=∠FEA﹣∠O′CA=115°﹣90°=25°，∴显示屏O′B′应绕点O′按顺时针方向旋转25度．24、（1）见详解；（2）①见详解；②120°【分析】教材呈现：证明△ADE∽△ABC即可解决问题．结论应用：（1）首先证明△ADE是等边三角形，推出AD＝AE，BD＝CE，再利用三角形的中位线定理即可证明．（2）利用三角形的中位线定理以及平行线的性质解决问题即可．【详解】教材呈现：证明：∵点D，E分别是AB，AC的中点，∴，∵∠A＝∠A，∴△ADE∽△ABC，∴∠ADE＝∠ABC，，∴DE∥BC，DE＝BC．结论应用：（1）证明：∵△ABC是等边三角形，∴AB＝AC，∠ABC＝∠ACB＝60°，∵DE∥AB，∴∠ABC＝∠ADE＝60°，∠ACB＝∠AED＝60°，∴∠ADE＝∠AED＝60°，∴△ADE是等边三角形，∴AD＝AE，∴BD＝CE，∵EM＝MD，EN＝NB，∴MN＝BD，∵BN＝NE，BP＝PC，∴PN＝EC，∴NM＝NP．（2）∵EM＝MD，E