MXT-高中数学-同角三角函数基本关系及诱导公式

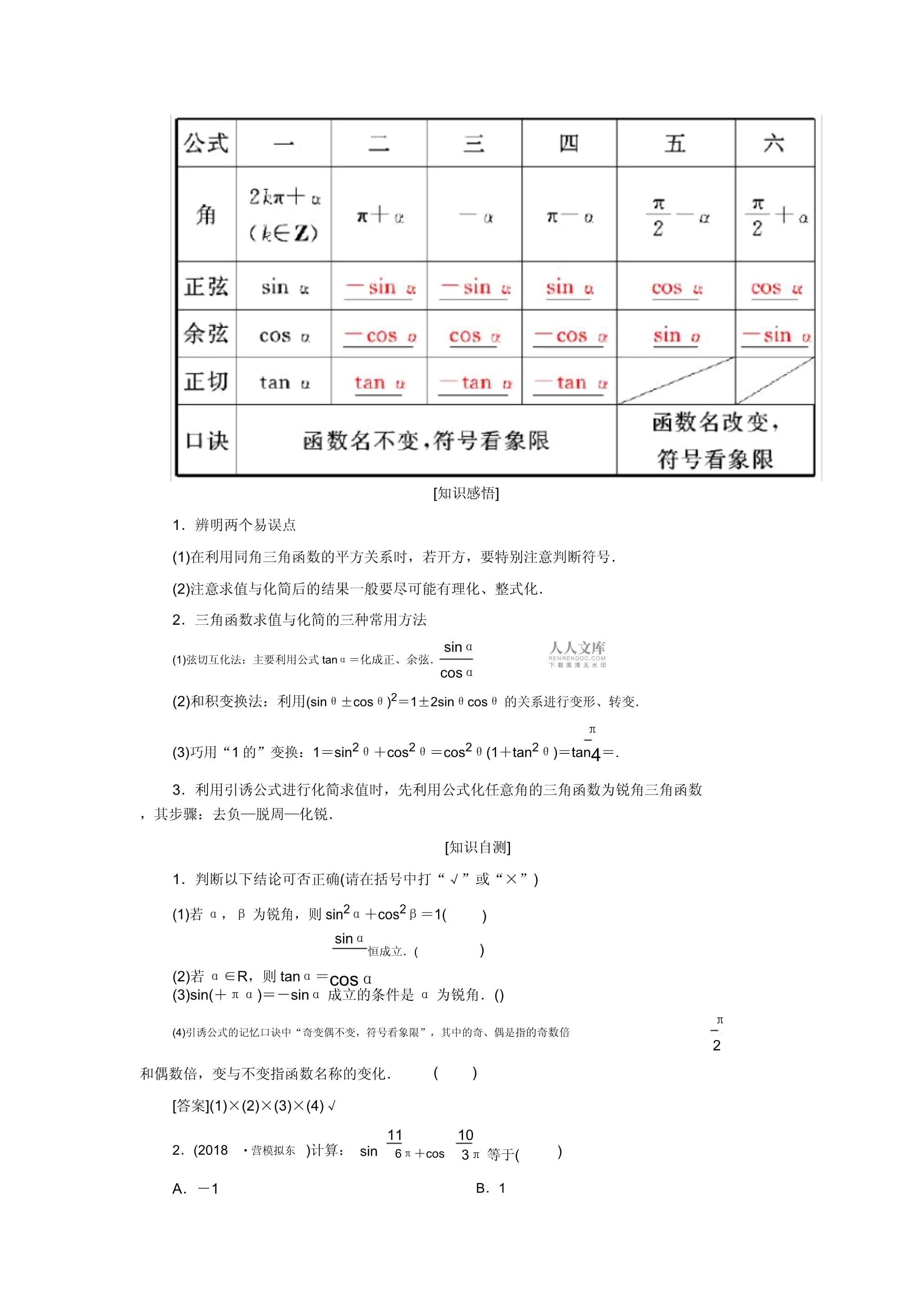
同角三角函数基本关系及引诱公式◆高考导航·顺风出发◆最新考纲常有题型1.理解同角三角函数的基本关系式：sin2α＋2sinα＝tanα.本节在高考中应用很广，比较灵便，常以选cosα＝1，cosα2.能利用单位圆中的三角函数线推导出π择题，填空题形式出现，5分左右.2±α，π±α的正弦、余弦、正切的引诱公式.[知识梳理]1．同角三角函数的基本关系(1)平方关系：sin2α＋cos2α＝1.sinα(2)商数关系：＝tanα.cosα2．三角函数的引诱公式[知识感悟]1．辨明两个易误点(1)在利用同角三角函数的平方关系时，若开方，要特别注意判断符号．(2)注意求值与化简后的结果一般要尽可能有理化、整式化．2．三角函数求值与化简的三种常用方法sinα(1)弦切互化法：主要利用公式tanα＝化成正、余弦．cosα(2)和积变换法：利用(sinθ±cosθ)2＝1±2sinθcosθ的关系进行变形、转变．π(3)巧用“1的”变换：1＝sin2θ＋cos2θ＝cos2θ(1＋tan2θ)＝tan4＝.3．利用引诱公式进行化简求值时，先利用公式化任意角的三角函数为锐角三角函数，其步骤：去负—脱周—化锐．[知识自测]1．判断以下结论可否正确(请在括号中打“√”或“×”)(1)若α，β为锐角，则sin2α＋cos2β＝1()sinα)恒成立．((2)若α∈R，则tanα＝cosα(3)sin(＋πα)＝－sinα成立的条件是α为锐角．()π(4)引诱公式的记忆口诀中“奇变偶不变，符号看象限”，其中的奇、偶是指的奇数倍2和偶数倍，变与不变指函数名称的变化．[答案](1)×(2)×(3)×(4)√

(

)11

102．(2018

·营模拟东

)计算：

sin

6π＋cos

3π等于(

)A．－1

B．1C．0D.1－3221155π1[解析]∵sin6π＝sinπ＋6π＝－sin6＝－2，104π4π1cos3π＝cos2π＋3＝cos3＝－2，∴sin11106π＋cos3π＝－1.[答案]A3．化简2sin2α－21＝________.1－2cosα[解析]sin2α＋sin2α－1sin2α－cos2α原式＝22＝22＝1.1－cosα－cosαsinα－cosα[答案]1题型一同角三角函数关系式的应用(高频考点题，多角打破)考向一知弦求弦π3π，则sin(π＋α)等于()＋α＝5，α∈0，21．已知sin23B．－3A.554D．－4C.55π3π[解析]因为sin2＋α＝5，α∈0，2，所以cosα＝3，所以sinα＝4，554所以sin(π＋α)＝－sinα＝－.[答案]D考向二知弦求切2．(2018辽·宁省五校高三联考)已知cosππ3π)＋α＝3，且α∈，，则tanα＝(252243A.3B.4C．－334D．±4π334[解析]因为cos2＋α＝5，所以sinα＝－5，显然α在第三象限，所以cosα＝－5，故tanα＝34.[答案]B考向三知切求弦3．若α是三角形的内角，且tanα＝－1，则sinα＋cosα的值为________.311sin2α＋cos2α＝1，[解析]由tanα＝－3，得sinα＝－3cosα，将其代入得10cos2α＝1，∴cos2α＝9，易知cosα＜0，9103101010∴cosα＝－10，sinα＝10，故sinα＋cosα＝－5.10[答案]－5考向四巧用sin2α＋cos2α＝1.4．sin21°＋sin22°＋＋sin289°＝______.[解析]原式＝(sin21°＋sin289°)＋(sin22°＋sin288°)＋＋(sin244°＋sin246°)＋sin245°＝222222111＝1＋1＋1＋＋1＋＝44(sin1°＋cos1°)＋(sin2°＋cos2°)＋＋(sin44°＋cos44°)＋22.44个21[答案]442考向五sinα、cosα的齐次式的应用5．已知sinα＋3cosα)＝5，则sin2α－sinαcosα的值为(3cosα－sinα12A．－5B．－512C.5D.5[解析]tanα＋3＝5，∴tanα＝2.依题意得：3－tanαsin2α－sinαcosα∴sin2α－sinαcosα＝22sinα＋cosαtan2α－tanα22－22＝tan2α＋1＝22＋1＝5.[答案]D考向六sinα±cosα关系式的应用16．已知α是三角形的内角，且sinα＋cosα＝5.(1)求tanα的值；1(2)把cos2α－sin2α用tanα表示出来，并求其值．sinα＋cosα＝1①[解](1)法一：联立方程5，sin2α＋cos2α＝1，②由①得cosα＝1－sinα，将其代入②，整理得25sin2α－5sinα－12＝0.54sinα＝5，∴tanα＝－4∵α是三角形内角，∴33.cosα＝－5，法二：∵sinα＋cosα＝1，∴(sinα＋cosα)2＝12，55即1＋2sinαcosα＝1，∴2sinαcosα＝－24，2525(sinα－cosα)2＝1－2sinαcosα＝1＋24＝49.2525sinαcosα＝－12＜0且0＜α＜π，25sinα＞0，cosα＜0，∴sinα－cosα＞0.7∴sinα－cosα＝5.14sinα＋cosα＝5，得sinα＝5，∴tanα＝－4由3，3.sinα－cosα＝7，cosα＝－55sin2α＋cos2α(2)21sin2α＋cos2αcos2αtan2α＋12＝22＝22＝2.cosα－sinαcosα－sinαcosα－sinα1－tanαcos2αtanα＝－43，1tan2α＋1－42＋125∴232＝2＝4＝－7.cosα－sinα1－tanα21－－3方法感悟同角三角函数基本关系式的应用技巧技巧解读适合题型主要利用公式sinθtanθ＝化成正弦、余弦，cosθ切弦互化sinθ表达式中含有sinθ，cosθ与tanθ也许利用公式＝tanθ化成正切cosθπ“1的”变换1＝sin2θ＋cos2θ＝cos2θ(1＋tan2θ)＝tan4＝表达式中需要利用“1转”化(sinθ±cosθ)2?2sinθcosθ和积变换利用(sinθ±cosθ)2＝1±2sinθcosθ的关系进表达式中含有sinθ±cosθ或sin行变形、转变θcosθ【针对补偿】1．(福建高考)若sinα＝－5tanα的值等于()13，且α为第四象限角，则1212A.5B．－555C.12D．－12[解析]法一：因为α为第四象限的角，故cosα＝1－sin2α＝1－－52＝12，13135所以tanα＝sinα－135＝＝－12.cosα1213法二：因为α是第四象限角，且sinα＝－5，所以可在α的终边上取一点P(12，－5)，13则tanα＝yx＝－125.[答案]D2．已知sinα－cosα＝2，α∈(0，π)，则tanα等于()2A．－1B．－22C.2D．1[解析]由

sinα－cosα＝2，sin2α＋cos2α＝1，消去sinα得2cos2α＋22cosα＋1＝0，即(2cosα＋1)2＝0，∴cosα＝－22.又α∈(0，π)，∴α＝3π3π＝－1.4.∴tanα＝tan4[答案]A3．化简：(1＋tan2α)(1－sin2α)＝________.[解析]22sin2α2cos2α＋sin2α2α＝1.(1＋tanα)(1－sinα＝)1＋cos2α·cosα＝cos2αcos[答案]1题型二引诱公式的应用(重点保分题，共同商议)(1)sin(－1200°)cos1290°＋cos(－1020°)·－sin(1050°)＝______.(2)设f(α)＝2sinπ＋αcosπ－α－cosπ＋α，其中1＋2sinα≠0，则f－23π＝______.3ππ61＋sin2α＋cos2＋α－sin22＋α[解析](1)原式＝－sin1200°cos1－290cos°1020°sin1050°＝－sin(3×360°＋120°)cos(3×360°＋210°)－cos(2×360°＋300°)sin(2×360°＋330°)＝－sin120°cos210－°cos300°sin330°＝－sin(180°－60°)cos(180＋°30°)－cos(360°－60°)·sin(360－30°°)＝sin60°cos30＋°cos60°sin30＝°3×3＋1×1＝1.2222－2sinα－cosα＋cosα(2)∵f(α)＝1＋sin2α＋sinα－cos2α2sinαcosα＋cosαcosα1＋2sinα1，＝＝＝2sin2α＋sinαsinα1＋2sinαtanα23π123π＝11∴f－6＝tan－π＝π＝3.6tan－4π＋tan66[答案](1)1(2)3方法感悟利用引诱公式化简三角函数的基本思路和化简要求：基本思路：①解析结构特点，选择适合公式；②利用公式化成单角三角函数；③整理得最简形式．化简要求：①化简过程是恒等变形；结果要求项数尽可能少，次数尽可能低，结构尽可能简单，能求值的要求出值．【针对补偿】cos350－°2sin160°)4．计算：－190°＝(sin3A．－3B．－23C.2D.3[解析]cos360°－10°－2sin180°－20°原式＝－sin180°＋10°13cos10－°2sin30°－10°cos10－°22cos10－°2sin10°＝－－sin10°＝sin10°＝3.[答案]Dtanπ＋αcos2π＋αsinα－3π2＝________.5．化简：cos－α－3πsin－3π－αtanαcosαsin－2π＋π[解析](1)原式＝α＋2cos3π＋α[－sin3π＋α]π＋αtanαcosαcosαtanαcosαsinαcosαtanαcosαsin2＝＝＝－sinα＝－·＝－1.－cosαsinα－cosαsinαcosαsinα[答案]－1题型三巧用引诱公式(高频考点题，多角打破)π3(2018·皖北模拟)若sin＋α＝，则65πcos3－α＝()33A．－5B.544C.5D．－5ππππ3[解析]cos3－α＝cos2－6＋α＝sin6＋α＝5，应选B.[答案]Bπ已知sinα－5＝a(a≠±1，a≠0)，求tanα＋9π5cosα＋14πα－11π＋的值．5·tan526πcos－α5tanα＋9π5[解]cosα＋14πα－11π＋5·tan526πcos5－αtanα－πππ5＝－cosα－5·tanα－5＋π－cos5－αsinα－π＝－sinπ5α－5－cos2α－π5a2＝a3－2a＝－a－1－a2.1－a方法感悟πππππ巧用相关角的关系会简化解题过程．常有的互余关系有3－α与6＋α；3＋α与6－α；4＋ππ2ππ3πα与4－α等，常有的互补关系有3＋θ与3－θ；4＋θ与4－θ等．【针对补偿】π35π6．已知tan－α＝3，则tan＋α＝________.665ππ[解析]tan6＋α＝tanπ－6＋αππ3＝tanπ－6－α＝－tan6－α＝－3.[答案]3－3π22π7．已知cos6－α＝3，则sinα－3＝________.π2π＝－π[解析]∵－α＋α－3，622πππ所以sinα－3＝sin－2－6－α＝－sinππ＝－cosπ2＋－α－α＝－3.266[答案]2－38．(2016全·国乙卷)已知θ是第四象限角，且sinθ＋π＝3，则tanθ－π＝________.454[解析]由题意知sinθ＋π＝3，θ是第四象限角，45π所以cosθ＋4＞0，所以cosθ＋π1－sin2θ＋π44＝4＝.5则tanθ－π＝tanππ4θ＋－24ππsin2－θ＋4＝－ππcos2－θ＋4πcosθ＋4＝－πsinθ＋4454＝－×＝－.533[答案]4－3◆牛刀小试·成功靠岸◆课堂达标(十七)[A基础牢固练]1．(2018济·南质检)α∈ππ)－，，sinα＝－3，则cos(－α)的值为(2254433A．－5B.5C.5D．－5[解析]ππ因为α∈－，2，sinα＝－3，25所以cosα＝4，即cos(－α)＝4，应选B.55[答案]B2．已知函数f(x)＝asin(xπ＋α)＋bcos(πx＋β)，且f(4)＝3，则f(2018)的值为()A．－1B．1C．3D．－3[解析]∵f(4)＝asin(4＋πα)＋bcos(4π＋β)＝asinα＋bcosβ＝3，∴f(2018)＝asin(2018π＋α)＋bcos(2018π＋β)＝asinα＋bcosβ＝3.即f(2018)＝3.[答案]Cπ3．(2018石·家庄模拟)已知α为锐角，且2tan(－πα)－3cos2＋β＋5＝0，tan(π＋α)＋6sin(π＋β)＝1，则sinα的值是()3537A.5B.73101C.10D.3[解析]由已知可得－2tanα＋3sinβ＋5＝0，tanα－6sinβ＝1，解得tanα＝3，故sinα＝31010.[答案]Cπ4．已知α和β的终边关于直线y＝x对称，且β＝－3，则sinα等于()33A．－2B.211C．－2D.2ππ[解析]因为α和β的终边关于直线y＝x对称，所以α＋β＝2kπ＋2(k∈Z)．又β＝－3，5π1所以α＝2kπ＋6(k∈Z)，即得sinα＝2.[答案]D5．已知－π112的值为()<α<0，sinα＋cosα＝，则225cosα－sinα77A.5B.252524C.7D．－2511[解析]∵sinα＋cosα＝5，∴1＋sin2α＝25，24π即sin2α＝－25，又∵－2<α<0，∴cosα－sinα>0.7∴cosα－sinα＝1－sin2α＝5，∴11＝25＝7.cos2α－sin2αcosα＋sinαcosα－sinα[答案]Cπ6．(2018辽·宁沈阳三模)若sinα＋3sin＋α＝0，则cos2α的值为()233A．－5B.544C．－5D.5[解析]π＝0，则sinα＋3cosα＝0，可得：tanα＝sinα由sinα＋3sin(＋α)＝－3；则cos2α2cosα1－tan2α1－94＝cos2α－sin2α＝tan2α＋1＝1＋9＝－5.应选C.[答案]Ctanπ－αcos2π－αsin－α＋3π7．化简：2＝______.cos－α－πsin－π－αtanα·cosα·－cosα[解析]原式＝cosπ＋α·－sinπ＋αsinα·cosαtanα·cosα·cosαcosα＝－cosα·sinα＝－sinα＝－1.[答案]－1sinsin

8．已知角θ的极点在坐标原点，始边与x轴正半轴重合，终边在直线2x－y＝0上，则3π()2＋θ＋cosπ－θ＝________.π2－θ－sinπ－θ[解析]由题意可得tanθ＝2，原式＝－cosθ－cosθ－2＝＝2.cosθ－sinθ1－tanθ[答案]2π＝a(|a|≤1)，则cos5π＋sin2π的值是______．9．已知cos－θ＋θ－θ6635ππ[解析]cos6＋θ＝cosπ－6－θπ＝－cos6－θ＝－a.2ππππsin3－θ＝sin2＋6－θ＝cos6－θ＝a，5π2π∴cos6＋θ＋sin3－θ＝0.[答案]010．已知sin(31，求cosπ＋θ＋＋πθ)＝3cosθ[cosπ－θ－1]cosθ－2π的值．3π3πsinθ－2cosθ－π－sin2＋θ11[解]∵sin(3＋πθ)＝－sinθ＝3，∴sinθ＝－3.∴原式＝－cosθ＋cosθcosθ－cosθ－1cosθ·－cosθ＋cosθ＝1＋cosθ＝1＋1＝2＝2＝2＝18.1＋cosθ－cos2θ＋cosθ1＋cosθ1－cosθ1－cos2θsin2θ12－3[B能力提升练]1．(2018厦·门模拟)已知cos31＝°a，则sin239°·tan的149值是°()1－a2B.1－a2A.aa2－1D．－1－a2C.a[解析]sin239°·tan149°＝sin(270－°31°)·tan(180－31°＝)(－cos31°)－·(tan31°)＝sin31°＝1－a2.[答案]B2．设A，B，C为△ABC的三个内角，有以下表达式：(1)sin(A＋B)＋sinC；(2)cos(A＋B)＋cosC；A＋BC(3)tan2tan2；(4)sin2A＋B＋sin2C22.无论△ABC的形状如何变化，向来是常数的表达式有()A．1个B．2个C．3个D．4个[解析](1)sin(A＋B)＋sinC＝sin(－πC)＋sinC＝2sinC，不是常数；(2)cos(A＋B)＋cosC＝cos(－πC)＋cosC＝－cosC＋cosC＝0，是常数；A＋BCπCC(3)tan2tan2＝tan2－2tan2＝1，是常数；A＋BCπCCCC(4)sin2(2)＋sin22＝sin22－2＋sin22＝cos22＋sin22＝1，是常数．故向来是常数的表达式有3个，选C.[答案]Ccosα1＋tan2α＋sinα13．(2018新·疆阿勒泰二模)已知α为第二象限角，则1＋tan2α＝______.sin2α＋cos2αsin2α＋cos2α1＋sinα1，[解析]原式＝cosαcos2α＋sinαsin2α＝cosα|cosα||sinα|因为α是第二象限角，所以sinα＞0，cosα＜0，所以cosα1＋sinα1＝－1＋1＝0，|cosα||