2021直线与圆锥曲线的位置关系课件和练习(优秀)

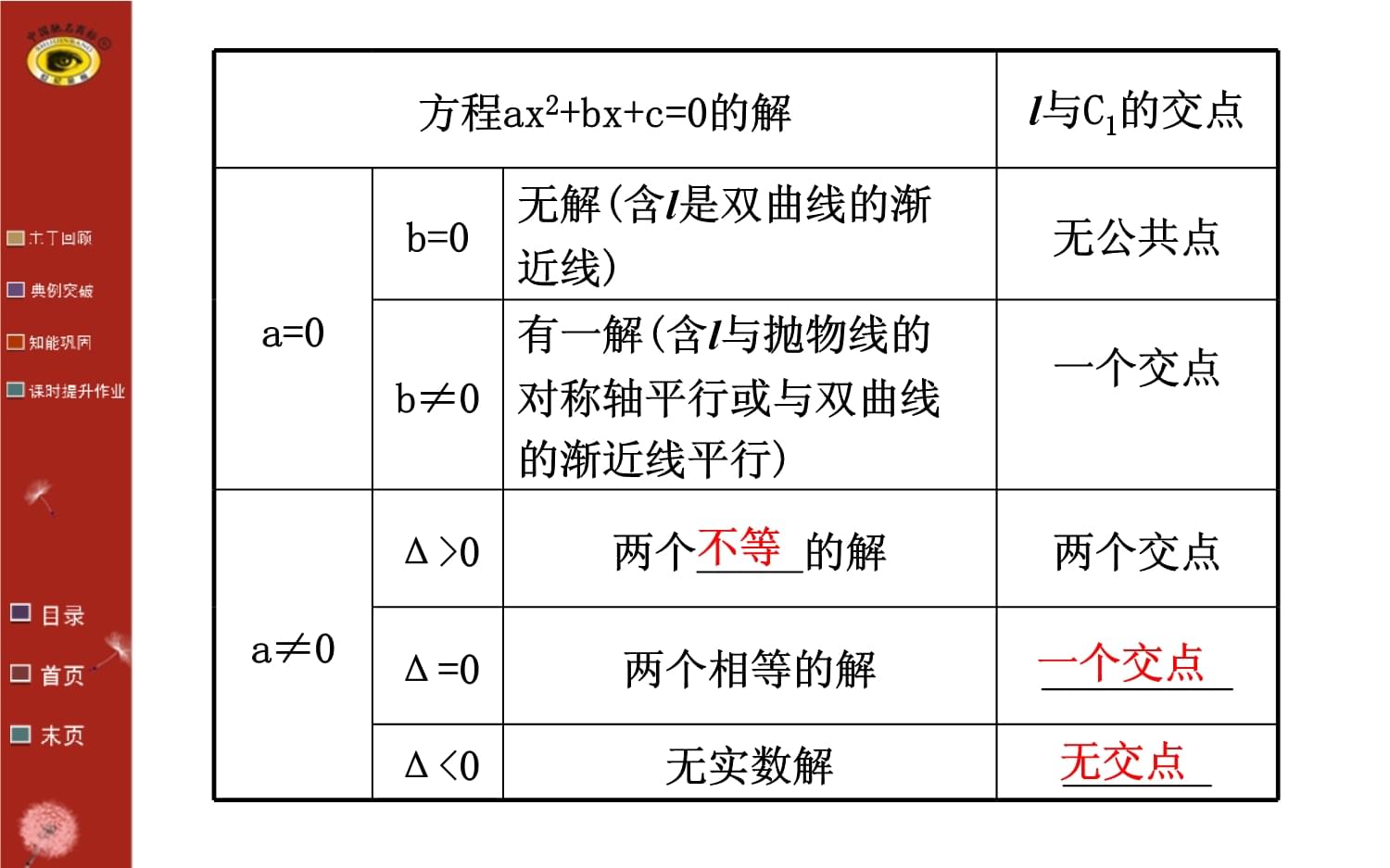
第九节直线与圆锥曲线的位置关系第九节直线与圆锥曲线的位置关系2021直线与圆锥曲线的位置关系课件和练习(优秀)1.直线与圆锥曲线的位置关系的判断方法直线与圆锥曲线的位置关系可分为：_____、_____、_____.这三种位置关系的判断方法为：设直线l:Ax+By+C=0(A2+B2≠0)，圆锥曲线C1：f(x,y)=0,由即将直线l的方程与圆锥曲线C1的方程联立，消去y便得到关于x的方程ax2+bx+c=0(当然，也可以消去x得到关于y的方程)，通过方程解的情况判断直线l与圆锥曲线C1的位置关系，见下表：相交相切相离1.直线与圆锥曲线的位置关系的判断方法相交相切相离方程ax2+bx+c=0的解

l与C1的交点

a=0b=0无解(含l是双曲线的渐近线)无公共点b≠0有一解(含l与抛物线的对称轴平行或与双曲线的渐近线平行)一个交点a≠0Δ>0两个_____的解两个交点Δ=0两个相等的解_________Δ<0无实数解_______不等一个交点无交点方程ax2+bx+c=0的解l与C1的交点a=0b=0无2.圆锥曲线的弦长设斜率为k(k≠0)的直线l与圆锥曲线C相交于A，B两点，A(x1,y1),B(x2,y2),则|AB|====2.圆锥曲线的弦长判断下列结论是否正确(请在括号中打“√”或“×”).(1)直线l与椭圆C相切的充要条件是：直线l与椭圆C只有一个公共点.()(2)直线l与双曲线C相切的充要条件是：直线l与双曲线C只有一个公共点.()(3)直线l与抛物线C相切的充要条件是：直线l与抛物线C只有一个公共点.()判断下列结论是否正确(请在括号中打“√”或“×”).(4)如果直线x=ty+a与圆锥曲线相交于A(x1,y1)，B(x2,y2)两点，则弦长()(5)若抛物线C上存在关于直线l对称的两点，则需满足直线l与抛物线C的方程联立消元得到的一元二次方程的判别式Δ>0.()(4)如果直线x=ty+a与圆锥曲线相交于A(x1,y1)，【解析】(1)正确，直线l与椭圆C只有一个公共点，则直线l与椭圆C相切，反之亦成立.(2)错误，因为直线l与双曲线C的渐近线平行时，也只有一个公共点，是相交，但并不相切.(3)错误，因为直线l与抛物线C的对称轴平行时，也只有一个公共点，是相交，但不相切.【解析】(1)正确，直线l与椭圆C只有一个公共点，则直线l与(4)正确，又x1=ty1+a,x2=ty2+a,(5)错误，应是以l为垂直平分线的线段AB所在的直线l′与抛物线方程联立，消元后所得一元二次方程的判别式Δ>0.答案:(1)√(2)×(3)×(4)√(5)×(4)正确，1.已知直线y=kx-k及抛物线y2=2px(p>0)，则()(A)直线与抛物线有一个公共点(B)直线与抛物线有两个公共点(C)直线与抛物线有一个或两个公共点(D)直线与抛物线可能无公共点【解析】选C.因为直线y=kx-k=k(x-1)恒过定点(1，0)，而点(1，0)在抛物线内部，故直线与抛物线有一个或两个公共点.1.已知直线y=kx-k及抛物线y2=2px(p>0)，则(2.已知以F1(-2，0)，F2(2，0)为焦点的椭圆与直线有且仅有一个交点，则椭圆的长轴长为()(A)(B)(C)(D)2.已知以F1(-2，0)，F2(2，0)为焦点的椭圆与直线【解析】选C.根据题意设椭圆方程为则将代入椭圆方程，得∵椭圆与直线有且仅有一个交点，∴b2=3,长轴长为【解析】选C.根据题意设椭圆方程为3.已知直线x-y-1=0与抛物线y=ax2相切，则a等于()(A)(B)(C)(D)4【解析】选C.将x-y-1=0，即y=x-1代入y=ax2得，ax2-x+1=0,∵直线与抛物线相切，∴Δ=(-1)2-4a=0，解得a=3.已知直线x-y-1=0与抛物线y=ax2相切，则a等于(4.已知双曲线x2-y2=1和斜率为的直线l交于A，B两点，当l变化时，线段AB的中点M的坐标满足的方程是_____.【解析】设A(x1,y1),B(x2,y2)，线段AB中点坐标(x0,y0),则两式相减，得(x1+x2)(x1-x2)=(y1+y2)(y1-y2),答案:y=2x4.已知双曲线x2-y2=1和斜率为的直线l交于A，B两5.过椭圆的左焦点且倾斜角为的直线被椭圆所截得的弦长为______.5.过椭圆的左焦点且倾斜角为的直线被椭【解析】设直线与椭圆的交点分别为A(x1,y1),B(x2,y2).由椭圆方程得：a=3，b=1，所以因此，直线方程为：与椭圆方程联立，消去y得：则所以答案：2

【解析】设直线与椭圆的交点分别为A(x1,考向1直线与圆锥曲线的位置关系的确定及应用【典例1】(1)已知椭圆若此椭圆与直线y=4x+m交于不同两点A，B，则实数m的取值范围是_____.(2)(2013·西安模拟)已知抛物线的方程为y2=4x,斜率为k的直线l过定点P(-2，1)，若直线l与抛物线只有一个公共点，则k的值为______.考向1直线与圆锥曲线的位置关系的确定及应用(3)(2012·安徽高考)如图，F1(-c,0),F2(c,0)分别是椭圆C:(a>b>0)的左、右焦点，过点F1作x轴的垂线交椭圆的上半部分于点P，过点F2作直线PF2的垂线交直线于点Q.①若点Q的坐标为(4，4)，求椭圆C的方程；②证明：直线PQ与椭圆C只有一个交点.(3)(2012·安徽高考)如图，【思路点拨】(1)(2)将直线与曲线方程联立转化为所得方程解的个数满足的条件求解.(3)①利用F1P⊥x轴，PF2⊥QF2，构建关于a,b,c的方程组，求解；②只需证明直线PQ与椭圆相切，即其方程联立消元后的一元二次方程有唯一解即可.【思路点拨】(1)(2)将直线与曲线方程联立转化为所得方程解【规范解答】(1)直线y=4x+m与椭圆联立，消去y得：67x2+32mx+4(m2-3)=0，由已知，其判别式Δ=(32m)2-4×67×4(m2-3)>0,解得：答案:【规范解答】(1)直线y=4x+m与椭圆联(2)由题意，得直线l的方程为y-1=k(x+2)，由得ky2-4y+4(2k+1)=0(*)(ⅰ)当k=0时，由方程(*)得y=1,方程组有一个解,此时，直线与抛物线只有一个公共点.(2)由题意，得直线l的方程为y-1=k(x+2)，(ⅱ)当k≠0时，方程(*)的判别式为Δ=-16(2k2+k-1).由Δ=0，即2k2+k-1=0，解得k=-1或∴当k=-1或时，方程组有一个解，此时，直线与抛物线只有一个公共点.综上可知，当k=-1或k=0或时，直线与抛物线只有一个公共点.答案:-1或0或(ⅱ)当k≠0时，方程(*)的判别式为Δ=-16(2k2+k(3)①由条件知，故直线PF2的斜率为因为PF2⊥F2Q，所以直线F2Q的方程为故由题设知，2a=4，解得a=2,c=1.故椭圆方程为(3)①由条件知，故直线PF2的斜率为②证明：直线PQ的方程为即将上式代入得x2+2cx+c2=0.(方法一)其判别式Δ=(2c)2-4c2=0,(方法二)解得x=-c,所以直线PQ与椭圆C只有一个交点.②证明：直线PQ的方程为【互动探究】若将本例题(1)中“此椭圆与直线y=4x+m交于不同两点A，B”变为“此椭圆上存在不同的两点A，B关于直线y=4x+m对称”，则实数m的取值范围如何？【互动探究】若将本例题(1)中“此椭圆与直线y=4x+m交于【解析】方法一：由于A，B两点关于直线y=4x+m对称，所以设直线AB的方程为即x=-4(y-b)，将其代入得:13y2-24by+12b2-3=0，其判别式Δ=(-24b)2-4×13×(12b2-3)>0，解得：①，设A(x1,y1),B(x2,y2),线段AB中点为M0(x0,y0),又M0在y=4x+m上，∴有②将②代入①解得【解析】方法一：由于A，B两点关于直线y=4x+m对称，所以方法二：设A(x1,y1),B(x2,y2),线段AB的中点M(x,y)，x1+x2=2x,y1+y2=2y,①②①②两式相减得即y1+y2=3(x1+x2),即y=3x,与y=4x+m联立得x=-m,y=-3m,而M(x,y)在椭圆的内部，则方法二：设A(x1,y1),B(x2,y2),【拓展提升】1.直线与圆锥曲线位置关系的判断方法用直线方程与圆锥曲线方程组成的方程组的解的个数，可以研究直线与圆锥曲线的位置关系，即用代数法研究几何问题，这是解析几何的重要思想方法.直线与圆锥曲线有无公共点或有几个公共点问题，实际上是研究方程组解的个数问题.【提醒】在研究方程组是否有实数解或实数解的个数问题时，要注意用好分类讨论和数形结合的思想方法.【拓展提升】2.曲线上存在关于直线对称的两点问题的解法及关键(1)解法：转化为过两对称点的直线与曲线的相交问题求解.(2)关键：用好两对称点的连线与对称轴垂直，且两点的中点在对称轴上.2.曲线上存在关于直线对称的两点问题的解法及关键【变式备选】(1)(2013·抚州模拟)若直线mx+ny=4与⊙O:x2+y2=4没有交点，则过点P(m,n)的直线与椭圆的交点个数是()(A)至多为1(B)2(C)1(D)0【解析】选B.由题意知：∴点P(m,n)在椭圆的内部，故所求交点个数是2个.【变式备选】(1)(2013·抚州模拟)若直线mx+ny=4(2)过双曲线的右焦点作直线l交双曲线于A，B两点，若|AB|=4，则这样的直线l有()(A)1条(B)2条(C)3条(D)4条【解析】选C.由于a=1，所以2a=2<4，数形结合知，当A，B在左右两支上时有2条，又过右焦点垂直于x轴的弦长恰好为4，故A，B同在右支上时，有1条.所以共3条.(2)过双曲线的右焦点作直线l交双曲线于A，考向2与弦长、弦中点及弦端点相关的问题【典例2】(1)已知抛物线C的顶点在坐标原点，焦点为F(0,-1),直线l与抛物线C相交于A，B两点.若线段AB的中点为(2，-2)，则直线l的方程为_____.(2)(2013·阜阳模拟)过抛物线y2=4x焦点F的直线与抛物线交于A，B两点，如果则直线AB的方程是_______.(3)(2013·南昌模拟)已知椭圆的中心在原点，焦点在x轴上，直线y=x+1与该椭圆相交于P，Q，且OP⊥OQ，求椭圆的方程.考向2与弦长、弦中点及弦端点相关的问题【思路点拨】(1)涉及弦的中点、斜率问题可利用点差法求解.(2)关键将弦的端点满足的向量关系转化为其横坐标大小关系，从而构建方程求解.(3)设出椭圆方程，与直线方程联立，利用OP⊥OQ及弦长构建方程(组)求解.【思路点拨】(1)涉及弦的中点、斜率问题可利用点差法求解.【规范解答】(1)由题意知，抛物线的方程为x2=-4y，设A(x1,y1),B(x2,y2)，且x1≠x2,联立方程得两式相减得∴直线l的方程为y+2=-(x-2),即y=-x.答案:x+y=0【规范解答】(1)由题意知，抛物线的方程为x2=-4y，设(2)由已知抛物线y2=4x的焦点F(1，0)，显然满足题意的直线斜率存在，设为k,则直线的方程为y=k(x-1),将其代入y2=4x,整理得k2x2-2(k2+2)x+k2=0(k2≠0)①其判别式Δ=16(k2+1)>0,设A(x1,y1),B(x2,y2)且由不妨设x1>x2.由①解得又得(1-x1,-y1)=2(x2-1,y2),得1-x1=2(x2-1),即x1+2x2=3,(2)由已知抛物线y2=4x的焦点F(1，0)，显然满足题意亦即：解得∴所求直线方程为答案:亦即：(3)设椭圆方程为ax2+by2=1且设P(x1,y1),Q(x2,y2).由得(a+b)x2+2bx+b-1=0.Δ=4b2-4(a+b)(b-1)=4(a+b-ab).∵OP⊥OQ,∴x1x2+y1y2=0.∴x1x2+(x1+1)(x2+1)=0,(3)设椭圆方程为ax2+by2=1∴2x1x2+x1+x2+1=0③①②代入③得∴a+b=2,∵|PQ|2=(x1-x2)2+(y1-y2)2=2(x1-x2)2=2［(x1+x2)2-4x1x2］=∴2x1x2+x1+x2+1=0③∵a+b=2且满足Δ>0.∴椭圆方程为∵a+b=2且满足Δ>0.【拓展提升】1.弦长的计算方法与技巧求弦长时可利用弦长公式，根据直线方程与圆锥曲线方程联立消元后得到的一元二次方程，利用根与系数的关系得到两根之和、两根之积的代数式，然后进行整体代入弦长公式求解.【提醒】注意两种特殊情况：(1)直线与圆锥曲线的对称轴平行或垂直；(2)直线过圆锥曲线的焦点.【拓展提升】2.弦中点问题的解法点差法在解决有关弦中点、弦所在直线的斜率、弦中点与原点连线斜率问题时可简化运算，但要注意直线斜率是否存在.3.与弦端点相关问题的解法解决与弦端点有关的向量关系、位置关系等问题的一般方法，就是将其转化为端点的坐标关系，再根据联立消元后的一元二次方程根与系数的大小关系，构建方程(组)求解.2.弦中点问题的解法【变式训练】设椭圆C：(a>b>0)过点(0，4)，离心率为(1)求椭圆C的方程.(2)求过点(3，0)且斜率为的直线被C所截线段的中点坐标.【变式训练】设椭圆C：(a>b>0)过点(0【解析】(1)将点(0，4)代入C的方程得∴b=4,∴椭圆C的方程为(2)过点(3，0)且斜率为的直线方程为设直线与C的交点为A(x1,y1),B(x2,y2)，将直线方程代入C的方程，得即x2-3x-8=0,解得∴AB的中点的横坐标纵坐标即所截线段的中点坐标为【解析】(1)将点(0，4)代入C的方程得∴b=4考向3探究性、存在性问题【典例3】(2012·福建高考)如图，椭圆E：(a>b>0)的左焦点为F1，右焦点为F2，离心率过F1的直线交椭圆于A，B两点，且△ABF2的周长为8.考向3探究性、存在性问题(1)求椭圆E的方程.(2)设动直线l：y=kx+m与椭圆E有且只有一个公共点P，且与直线x=4相交于点Q.试探究：在坐标平面内是否存在定点M，使得以PQ为直径的圆恒过点M？若存在，求出点M的坐标；若不存在，说明理由.(1)求椭圆E的方程.【思路点拨】(1)利用待定系数法求解，(2)假设存在点M满足题设条件，先探索出M必在x轴上，再根据以PQ为直径的圆恒过M点，即恒成立，求M点横坐标大小，从而判断点Ｍ是否存在.【思路点拨】(1)利用待定系数法求解，(2)假设存在点M满足【规范解答】方法一：(1)因为|AB|+|AF2|+|BF2|=8，即|AF1|+|F1B|+|AF2|+|BF2|=8，又|AF1|+|AF2|=|BF1|+|BF2|=2a,所以4a=8,a=2.又因为所以c=1,所以故椭圆E的方程是【规范解答】方法一：(1)因为|AB|+|AF2|+|BF2(2)由得(4k2+3)x2+8kmx+4m2-12=0.因为动直线l与椭圆E有且只有一个公共点P(x0,y0)，所以m≠0且Δ=0,即64k2m2-4(4k2+3)(4m2-12)=0，化简得4k2-m2+3=0.(*)此时所以(2)由得由得Q(4,4k+m).假设平面内存在定点M满足条件，由图形对称性知，点M必在x轴上.设M(x1,0)，则对满足(*)式的m,k恒成立.因为由得整理，得(**)由得Q(4,4k+m).由于(**)式对满足(*)式的m,k恒成立，所以解得x1=1.故存在定点M(1,0)，使得以PQ为直径的圆恒过点M.方法二：(1)同方法一.(2)由得(4k2+3)x2+8kmx+4m2-12=0.因为动直线l与椭圆E有且只有一个公共点P(x0,y0)，所以m≠0且Δ=0,由于(**)式对满足(*)式的m,k恒成立，所以即64k2m2-4(4k2+3)(4m2-12)=0，化简得4k2-m2+3=0.(*)此时所以由得Q(4,4k+m).假设平面内存在定点M满足条件，由图形对称性知，点M必在x轴上.即64k2m2-4(4k2+3)(4m2-12)=0，取k=0,此时以PQ为直径的圆为(x-2)2+交x轴于点M1(1,0),M2(3,0)；取m=2,此时Q(4,0)，以PQ为直径的圆为交x轴于点M3(1，0)，M4(4,0).所以若符合条件的点M存在，则M的坐标必为(1，0).以下证明M(1，0)就是满足条件的点:因为M的坐标为(1，0)，所以从而故恒有即存在定点M(1，0)，使得以PQ为直径的圆恒过点M.取k=0,此时以P【拓展提升】探究性、存在性问题的求解步骤(1)先假设存在,引入参数,根据题目条件列出关于参数的方程(组)或不等式(组).(2)解此方程(组)或不等式(组),若有解即存在,若无解则不存在.【拓展提升】探究性、存在性问题的求解步骤【变式训练】(2013·宝鸡模拟)已知：向量O为坐标原点，动点M满足：(1)求动点M的轨迹C的方程.(2)已知直线l1,l2都过点B(0,1)，且l1⊥l2，l1,l2与轨迹C分别交于点D,E，试探究是否存在这样的直线使得△BDE是等腰直角三角形.若存在，指出这样的直线共有几组(无需求出直线的方程)；若不存在，请说明理由.【变式训练】(2013·宝鸡模拟)已知：向量【解析】(1)方法一：设则∴动点M的轨迹为以A，A′为焦点，长轴长为4的椭圆.由2a=4，得a=2,∴动点M的轨迹C的方程为方法二:设点M(x,y),则【解析】(1)方法一：设则∴点M的轨迹C是以为焦点，长轴长为4的椭圆.∴动点M的轨迹C的方程为(2)轨迹C是椭圆点B(0,1)是它的上顶点，设满足条件的直线l1，l2存在，由题意知两直线斜率存在且不为零，不妨设直线l1的方程为y=kx+1(k＞0)①则直线l2的方程为②∴点M的轨迹C是以为焦点，长轴长为4的将①代入椭圆方程并整理得：(1+4k2)x2+8kx=0，可得则将②代入椭圆方程并整理得：(4+k2)x2-8kx=0，可得由△BDE是等腰直角三角形得|BD|=|BE|将①代入椭圆方程并整理得：(1+4k2)x2+8kx=0，可k3+4k=1+4k2k3-1=4k2-4k(k-1)(k2+k+1)=4k(k-1)③∴k=1或k2-3k+1=0④∵方程④的判别式Δ=5＞0，即方程④有两个不相等的实根，且不为1.∴方程③有三个互不相等的实根.即满足条件的直线l1，l2存在，共有3组．k3+4k=1+4k2k3-1=4k2-4k【满分指导】解答直线与圆锥曲线位置关系的综合问题【典例】(12分)(2012·北京高考)已知曲线C：(5-m)x2+(m-2)y2=8(m∈R).(1)若曲线C是焦点在x轴上的椭圆，求m的取值范围.(2)设m=4，曲线C与y轴的交点为A，B(点A位于点B的上方)，直线y=kx+4与曲线C交于不同的两点M，N，直线y=1与直线BM交于点G.求证：A，G，N三点共线.【满分指导】解答直线与圆锥曲线位置关系的综合问题【思路点拨】已知条件条件分析曲线C是焦点在x轴上的椭圆构建关于m的不等式组m=4得曲线C：x2+2y2=8直线y=kx+4与曲线C交于不同两点联立消元所得一元二次方程的判别式Δ>0A，G，N三点共线只需证kAN=kAG即可【思路点拨】已知条件条件分析曲线C是焦点在x轴上的椭圆构建关【规范解答】(1)曲线C是焦点在x轴上的椭圆，当且仅当

①

…………3分解得所以m的取值范围是……5分(2)当m=4时，曲线C的方程为x2+2y2=8,点A，B的坐标分别为(0，2)，(0，-2).……………6分由得(1+2k2)x2+16kx+24=0.…7分【规范解答】(1)曲线C是焦点在x轴上的椭圆，当且仅当因为直线与曲线C交于不同的两点，所以

②……8分设点M，N的坐标分别为(x1,y1),(x2,y2),则y1=kx1+4,y2=kx2+4,直线BM的方程为点G的坐标为………9分因为直线AN和直线AG的斜率分别为所以=因为直线与曲线C交于不同的两点，所以

…………11分即kAN=kAG.又AN与AG有公共点A，故A，G，N三点共线.…………………12分………………【失分警示】(下文①②③见规范解答过程)【失分警示】(下文①②③见规范解答过程)1.(2013·咸阳模拟)设抛物线y2=8x的准线与x轴交于点Q，若过点Q的直线l与抛物线有公共点，则直线l的斜率的取值范围是()(A)(B)［-2,2］(C)［-1,1］(D)［-4,4］1.(2013·咸阳模拟)设抛物线y2=8x的准线与x轴交于【解析】选C.由题意得Q(-2，0).设l的方程为y=k(x+2),代入y2=8x得k2x2+4(k2-2)x+4k2=0,∴当k=0时，直线l与抛物线恒有一个交点；当k≠0时,Δ=16(k2-2)2-16k4≥0,即k2≤1,∴-1≤k≤1,且k≠0,综上-1≤k≤1.【解析】选C.由题意得Q(-2，0).设l的方程为y=k(x2.(2013·九江模拟)直线3x-4y+4=0与抛物线x2=4y和圆x2+(y-1)2=1从左到右的交点依次为A，B，C，D.则的值为()(A)16(B)(C)4(D)2.(2013·九江模拟)直线3x-4y+4=0与抛物线x2【解析】选B.由得x2-3x-4=0，∴xA=-1,xD=4，直线3x-4y+4=0恰过抛物线的焦点F(0，1).【解析】选B.由得x2-3x-4=3.(2013·安庆模拟)已知双曲线方程是过定点P(2，1)作直线交双曲线于P1，P2两点，并使P(2，1)为P1P2的中点，则此直线方程是______.3.(2013·安庆模拟)已知双曲线方程是【解析】设点P1(x1,y1),P2(x2,y2),则由得从而所求方程为4x-y-7=0.将此直线方程与双曲线方程联立得14x2-56x+51=0,Δ>0，故此直线满足条件.答案:4x-y-7=0【解析】设点P1(x1,y1),P2(x2,y2),则由4.(2013·南昌模拟)在平面直角坐标系xOy中，O为坐标原点，动点P与两个定点M(1，0)，N(4，0)的距离之比为(1)求动点P的轨迹W的方程.(2)若直线l:y=kx+3与曲线W交于A，B两点，则曲线W上是否存在一点Q，使得若存在，求出此时直线l的斜率；若不存在，请说明理由.4.(2013·南昌模拟)在平面直角坐标系xOy中，O为坐标【解析】(1)设点P的坐标为(x,y)，依题意，知即化简得x2+y2=4,所以动点P的轨迹W的方程为x2+y2=4.【解析】(1)设点P的坐标为(x,y)，依题意，知(2)因为直线l:y=kx+3与曲线W相交于A，B两点，所以假设存在点Q，使得因为A，B在圆上，且由向量加法的平行四边形法则可知四边形OAQB为菱形，所以OQ与AB互相垂直且平分，所以原点O到直线l:y=kx+3的距离为1,即解得k2=8,经验证满足条件.所以存在点Q，使得(2)因为直线l:y=kx+3与曲线W相交于A，B两点，1.已知圆M：及定点点P是圆M上的动点，点Q在NP上，点G在MP上，且满足(1)求点G的轨迹C的方程.(2)过点K(2，0)作直线l,与曲线C交于A，B两点，O是坐标原点，设是否存在这样的直线l,使四边形OASB的对角线相等？若存在，求出直线l的方程；若不存在，说明理由.1.已知圆M：及定点【解析】(1)由Q为PN的中点，且GQ⊥PNGQ是PN的中垂线，|PG|=|GN|，∴|PM|=|GM|+|GP|=|GM|+|GN|=∴点G的轨迹是以M，N为焦点的椭圆，又a=3,∴C的方程为【解析】(1)由Q为PN的中点，且GQ(2)∵四边形OASB为平行四边形，假设存在直线l，使|OS|=|AB|四边形OASB为矩形OA⊥OB.若l的斜率不存在，则l的方程为x=2,由这与相矛盾，∴l的斜率存在.(2)∵四边形OASB为平行四边形，假设直线l的方程为y=k(x-2),A(x1,y1),B(x2,y2),

(9k2+4)x2-36k2x+36(k2-1)=0.∴y1y2=k(x1-2)·k(x2-2)由∴存在直线l:3x-2y-6=0或3x+2y-6=0满足条件.设直线l的方程为y=k(x-2),A(x1,y1),B(x22.如图，在x轴上方有一段曲线弧Γ，其端点A，B在x轴上(但不属于Γ)，对Γ上任一点P及点F1(-1，0)，F2(1，0)，满足：|PF1|+|PF2|=直线AP，BP分别交直线l:x=a于R，T两点.2.如图，在x轴上方有一段曲线(1)求曲线弧Γ的方程.(2)求|RT|的最小值(用a表示).(3)曲线弧Γ上是否存在点P，使△PRT为正三角形？若存在，求a的取值范围；若不存在，说明理由.(1)求曲线弧Γ的方程.【解析】(1)由椭圆的定义知，曲线弧Γ是以F1(-1，0)，F2(1，0)为焦点的半椭圆，c=1,b2=a2-c2=1.∴曲线弧Γ的方程为(2)由(1)知，曲线弧Γ的方程为设P(x0,y0),则有又从而直线AP，BP的方程为【解析】(1)由椭圆的定义知，曲线弧Γ是以F1(-1，0)，令x=a得R，T的纵坐标分别为将①代入②，得当且仅当|yR|=|yT|,即yR=-yT时，取等号.即|RT|的最小值是令x=a得R，T的纵坐标分别为(3)设P(x0,y0)，依题设，直线l∥y轴，若△PRT为正三角形，则必有∠PAB=30°,从而直线AP，BP的斜率存在，分别设为k1,k2,由(2)知，于是有矛盾.∴不存在点P，使△PRT为正三角形.(3)设P(x0,y0)，依题设，直线l∥y轴，若△PRT为2021直线与圆锥曲线的位置关系课件和练习(优秀)2021直线与圆锥曲线的位置关系课件和练习(优秀)8.每天只看目标，别老想障碍。19.学会宽容，意味着成长，秀木出木可吸纳更多的日月风华，舒展茁壮而更具成熟的力量。3、遇到会做的题：仔细;遇到不会做的题：冷静。18.如同磁铁吸引四周的铁粉，热情也能吸引周围的人，改变周围的情况。13.别人可以违背因果，别人可以害我们，打我们，毁谤我们。可是我们不能因此而憎恨别人，为什么?我们一定要保有一颗完整的本性和一颗清净的心。14.这个社会是存在不公平的，不要抱怨，因为没有用!人总是在反省中进步的!5.这或许是人的自然倾向，这样的话，结婚时为了年老后的保险。表面上是相爱，其实是衰老之后的一种保险。5.没有一种不通过蔑视、忍受和奋斗就可以征服的命运。12、人有时是要勉强自己的。我们需要一种来自自身的强有力的能量推动自己闯出一个新的境界来。19.过去不等于未来，没有失败，只有暂时停止成功。6.人的痛苦只能在生活和劳动中慢慢消磨掉，但朋友，没有什么灵丹妙药比得上劳动更能医治人的精神创伤。8、靠山山会倒，靠水水会流，靠自己永远不倒。2.推销产品要针对顾客的心，不要针对顾客的头。2.对于最有能力的领航人风浪总是格外的汹涌。12.昨晚多几分钟的准备，今天少几小时的麻烦。7.人也罢，花草和其他生物也罢，凡是过度想表现自己，就会使观众扫兴，减弱了它本来所具有的魅力。15、夫妇一条心，泥土变黄金。12.仔细思量一下就会明白：对对方的不信任，实际上就是对自我的不信任。推测对方的内心时，人就像把自己的生命反映到镜子中一样凝视着，再将其投影于对方，从而决定信任或不信任对方。13.知难而上，奋发图强，是竞争的作用;知难而退消极颓唐，也是竞争的作用。16.在真实的生命里，每桩伟业都由信心开始，并由信心跨出第一步。8.每天只看目标，别老想障碍。85第九节直线与圆锥曲线的位置关系第九节直线与圆锥曲线的位置关系2021直线与圆锥曲线的位置关系课件和练习(优秀)1.直线与圆锥曲线的位置关系的判断方法直线与圆锥曲线的位置关系可分为：_____、_____、_____.这三种位置关系的判断方法为：设直线l:Ax+By+C=0(A2+B2≠0)，圆锥曲线C1：f(x,y)=0,由即将直线l的方程与圆锥曲线C1的方程联立，消去y便得到关于x的方程ax2+bx+c=0(当然，也可以消去x得到关于y的方程)，通过方程解的情况判断直线l与圆锥曲线C1的位置关系，见下表：相交相切相离1.直线与圆锥曲线的位置关系的判断方法相交相切相离方程ax2+bx+c=0的解

l与C1的交点

a=0b=0无解(含l是双曲线的渐近线)无公共点b≠0有一解(含l与抛物线的对称轴平行或与双曲线的渐近线平行)一个交点a≠0Δ>0两个_____的解两个交点Δ=0两个相等的解_________Δ<0无实数解_______不等一个交点无交点方程ax2+bx+c=0的解l与C1的交点a=0b=0无2.圆锥曲线的弦长设斜率为k(k≠0)的直线l与圆锥曲线C相交于A，B两点，A(x1,y1),B(x2,y2),则|AB|====2.圆锥曲线的弦长判断下列结论是否正确(请在括号中打“√”或“×”).(1)直线l与椭圆C相切的充要条件是：直线l与椭圆C只有一个公共点.()(2)直线l与双曲线C相切的充要条件是：直线l与双曲线C只有一个公共点.()(3)直线l与抛物线C相切的充要条件是：直线l与抛物线C只有一个公共点.()判断下列结论是否正确(请在括号中打“√”或“×”).(4)如果直线x=ty+a与圆锥曲线相交于A(x1,y1)，B(x2,y2)两点，则弦长()(5)若抛物线C上存在关于直线l对称的两点，则需满足直线l与抛物线C的方程联立消元得到的一元二次方程的判别式Δ>0.()(4)如果直线x=ty+a与圆锥曲线相交于A(x1,y1)，【解析】(1)正确，直线l与椭圆C只有一个公共点，则直线l与椭圆C相切，反之亦成立.(2)错误，因为直线l与双曲线C的渐近线平行时，也只有一个公共点，是相交，但并不相切.(3)错误，因为直线l与抛物线C的对称轴平行时，也只有一个公共点，是相交，但不相切.【解析】(1)正确，直线l与椭圆C只有一个公共点，则直线l与(4)正确，又x1=ty1+a,x2=ty2+a,(5)错误，应是以l为垂直平分线的线段AB所在的直线l′与抛物线方程联立，消元后所得一元二次方程的判别式Δ>0.答案:(1)√(2)×(3)×(4)√(5)×(4)正确，1.已知直线y=kx-k及抛物线y2=2px(p>0)，则()(A)直线与抛物线有一个公共点(B)直线与抛物线有两个公共点(C)直线与抛物线有一个或两个公共点(D)直线与抛物线可能无公共点【解析】选C.因为直线y=kx-k=k(x-1)恒过定点(1，0)，而点(1，0)在抛物线内部，故直线与抛物线有一个或两个公共点.1.已知直线y=kx-k及抛物线y2=2px(p>0)，则(2.已知以F1(-2，0)，F2(2，0)为焦点的椭圆与直线有且仅有一个交点，则椭圆的长轴长为()(A)(B)(C)(D)2.已知以F1(-2，0)，F2(2，0)为焦点的椭圆与直线【解析】选C.根据题意设椭圆方程为则将代入椭圆方程，得∵椭圆与直线有且仅有一个交点，∴b2=3,长轴长为【解析】选C.根据题意设椭圆方程为3.已知直线x-y-1=0与抛物线y=ax2相切，则a等于()(A)(B)(C)(D)4【解析】选C.将x-y-1=0，即y=x-1代入y=ax2得，ax2-x+1=0,∵直线与抛物线相切，∴Δ=(-1)2-4a=0，解得a=3.已知直线x-y-1=0与抛物线y=ax2相切，则a等于(4.已知双曲线x2-y2=1和斜率为的直线l交于A，B两点，当l变化时，线段AB的中点M的坐标满足的方程是_____.【解析】设A(x1,y1),B(x2,y2)，线段AB中点坐标(x0,y0),则两式相减，得(x1+x2)(x1-x2)=(y1+y2)(y1-y2),答案:y=2x4.已知双曲线x2-y2=1和斜率为的直线l交于A，B两5.过椭圆的左焦点且倾斜角为的直线被椭圆所截得的弦长为______.5.过椭圆的左焦点且倾斜角为的直线被椭【解析】设直线与椭圆的交点分别为A(x1,y1),B(x2,y2).由椭圆方程得：a=3，b=1，所以因此，直线方程为：与椭圆方程联立，消去y得：则所以答案：2

【解析】设直线与椭圆的交点分别为A(x1,考向1直线与圆锥曲线的位置关系的确定及应用【典例1】(1)已知椭圆若此椭圆与直线y=4x+m交于不同两点A，B，则实数m的取值范围是_____.(2)(2013·西安模拟)已知抛物线的方程为y2=4x,斜率为k的直线l过定点P(-2，1)，若直线l与抛物线只有一个公共点，则k的值为______.考向1直线与圆锥曲线的位置关系的确定及应用(3)(2012·安徽高考)如图，F1(-c,0),F2(c,0)分别是椭圆C:(a>b>0)的左、右焦点，过点F1作x轴的垂线交椭圆的上半部分于点P，过点F2作直线PF2的垂线交直线于点Q.①若点Q的坐标为(4，4)，求椭圆C的方程；②证明：直线PQ与椭圆C只有一个交点.(3)(2012·安徽高考)如图，【思路点拨】(1)(2)将直线与曲线方程联立转化为所得方程解的个数满足的条件求解.(3)①利用F1P⊥x轴，PF2⊥QF2，构建关于a,b,c的方程组，求解；②只需证明直线PQ与椭圆相切，即其方程联立消元后的一元二次方程有唯一解即可.【思路点拨】(1)(2)将直线与曲线方程联立转化为所得方程解【规范解答】(1)直线y=4x+m与椭圆联立，消去y得：67x2+32mx+4(m2-3)=0，由已知，其判别式Δ=(32m)2-4×67×4(m2-3)>0,解得：答案:【规范解答】(1)直线y=4x+m与椭圆联(2)由题意，得直线l的方程为y-1=k(x+2)，由得ky2-4y+4(2k+1)=0(*)(ⅰ)当k=0时，由方程(*)得y=1,方程组有一个解,此时，直线与抛物线只有一个公共点.(2)由题意，得直线l的方程为y-1=k(x+2)，(ⅱ)当k≠0时，方程(*)的判别式为Δ=-16(2k2+k-1).由Δ=0，即2k2+k-1=0，解得k=-1或∴当k=-1或时，方程组有一个解，此时，直线与抛物线只有一个公共点.综上可知，当k=-1或k=0或时，直线与抛物线只有一个公共点.答案:-1或0或(ⅱ)当k≠0时，方程(*)的判别式为Δ=-16(2k2+k(3)①由条件知，故直线PF2的斜率为因为PF2⊥F2Q，所以直线F2Q的方程为故由题设知，2a=4，解得a=2,c=1.故椭圆方程为(3)①由条件知，故直线PF2的斜率为②证明：直线PQ的方程为即将上式代入得x2+2cx+c2=0.(方法一)其判别式Δ=(2c)2-4c2=0,(方法二)解得x=-c,所以直线PQ与椭圆C只有一个交点.②证明：直线PQ的方程为【互动探究】若将本例题(1)中“此椭圆与直线y=4x+m交于不同两点A，B”变为“此椭圆上存在不同的两点A，B关于直线y=4x+m对称”，则实数m的取值范围如何？【互动探究】若将本例题(1)中“此椭圆与直线y=4x+m交于【解析】方法一：由于A，B两点关于直线y=4x+m对称，所以设直线AB的方程为即x=-4(y-b)，将其代入得:13y2-24by+12b2-3=0，其判别式Δ=(-24b)2-4×13×(12b2-3)>0，解得：①，设A(x1,y1),B(x2,y2),线段AB中点为M0(x0,y0),又M0在y=4x+m上，∴有②将②代入①解得【解析】方法一：由于A，B两点关于直线y=4x+m对称，所以方法二：设A(x1,y1),B(x2,y2),线段AB的中点M(x,y)，x1+x2=2x,y1+y2=2y,①②①②两式相减得即y1+y2=3(x1+x2),即y=3x,与y=4x+m联立得x=-m,y=-3m,而M(x,y)在椭圆的内部，则方法二：设A(x1,y1),B(x2,y2),【拓展提升】1.直线与圆锥曲线位置关系的判断方法用直线方程与圆锥曲线方程组成的方程组的解的个数，可以研究直线与圆锥曲线的位置关系，即用代数法研究几何问题，这是解析几何的重要思想方法.直线与圆锥曲线有无公共点或有几个公共点问题，实际上是研究方程组解的个数问题.【提醒】在研究方程组是否有实数解或实数解的个数问题时，要注意用好分类讨论和数形结合的思想方法.【拓展提升】2.曲线上存在关于直线对称的两点问题的解法及关键(1)解法：转化为过两对称点的直线与曲线的相交问题求解.(2)关键：用好两对称点的连线与对称轴垂直，且两点的中点在对称轴上.2.曲线上存在关于直线对称的两点问题的解法及关键【变式备选】(1)(2013·抚州模拟)若直线mx+ny=4与⊙O:x2+y2=4没有交点，则过点P(m,n)的直线与椭圆的交点个数是()(A)至多为1(B)2(C)1(D)0【解析】选B.由题意知：∴点P(m,n)在椭圆的内部，故所求交点个数是2个.【变式备选】(1)(2013·抚州模拟)若直线mx+ny=4(2)过双曲线的右焦点作直线l交双曲线于A，B两点，若|AB|=4，则这样的直线l有()(A)1条(B)2条(C)3条(D)4条【解析】选C.由于a=1，所以2a=2<4，数形结合知，当A，B在左右两支上时有2条，又过右焦点垂直于x轴的弦长恰好为4，故A，B同在右支上时，有1条.所以共3条.(2)过双曲线的右焦点作直线l交双曲线于A，考向2与弦长、弦中点及弦端点相关的问题【典例2】(1)已知抛物线C的顶点在坐标原点，焦点为F(0,-1),直线l与抛物线C相交于A，B两点.若线段AB的中点为(2，-2)，则直线l的方程为_____.(2)(2013·阜阳模拟)过抛物线y2=4x焦点F的直线与抛物线交于A，B两点，如果则直线AB的方程是_______.(3)(2013·南昌模拟)已知椭圆的中心在原点，焦点在x轴上，直线y=x+1与该椭圆相交于P，Q，且OP⊥OQ，求椭圆的方程.考向2与弦长、弦中点及弦端点相关的问题【思路点拨】(1)涉及弦的中点、斜率问题可利用点差法求解.(2)关键将弦的端点满足的向量关系转化为其横坐标大小关系，从而构建方程求解.(3)设出椭圆方程，与直线方程联立，利用OP⊥OQ及弦长构建方程(组)求解.【思路点拨】(1)涉及弦的中点、斜率问题可利用点差法求解.【规范解答】(1)由题意知，抛物线的方程为x2=-4y，设A(x1,y1),B(x2,y2)，且x1≠x2,联立方程得两式相减得∴直线l的方程为y+2=-(x-2),即y=-x.答案:x+y=0【规范解答】(1)由题意知，抛物线的方程为x2=-4y，设(2)由已知抛物线y2=4x的焦点F(1，0)，显然满足题意的直线斜率存在，设为k,则直线的方程为y=k(x-1),将其代入y2=4x,整理得k2x2-2(k2+2)x+k2=0(k2≠0)①其判别式Δ=16(k2+1)>0,设A(x1,y1),B(x2,y2)且由不妨设x1>x2.由①解得又得(1-x1,-y1)=2(x2-1,y2),得1-x1=2(x2-1),即x1+2x2=3,(2)由已知抛物线y2=4x的焦点F(1，0)，显然满足题意亦即：解得∴所求直线方程为答案:亦即：(3)设椭圆方程为ax2+by2=1且设P(x1,y1),Q(x2,y2).由得(a+b)x2+2bx+b-1=0.Δ=4b2-4(a+b)(b-1)=4(a+b-ab).∵OP⊥OQ,∴x1x2+y1y2=0.∴x1x2+(x1+1)(x2+1)=0,(3)设椭圆方程为ax2+by2=1∴2x1x2+x1+x2+1=0③①②代入③得∴a+b=2,∵|PQ|2=(x1-x2)2+(y1-y2)2=2(x1-x2)2=2［(x1+x2)2-4x1x2］=∴2x1x2+x1+x2+1=0③∵a+b=2且满足Δ>0.∴椭圆方程为∵a+b=2且满足Δ>0.【拓展提升】1.弦长的计算方法与技巧求弦长时可利用弦长公式，根据直线方程与圆锥曲线方程联立消元后得到的一元二次方程，利用根与系数的关系得到两根之和、两根之积的代数式，然后进行整体代入弦长公式求解.【提醒】注意两种特殊情况：(1)直线与圆锥曲线的对称轴平行或垂直；(2)直线过圆锥曲线的焦点.【拓展提升】2.弦中点问题的解法点差法在解决有关弦中点、弦所在直线的斜率、弦中点与原点连线斜率问题时可简化运算，但要注意直线斜率是否存在.3.与弦端点相关问题的解法解决与弦端点有关的向量关系、位置关系等问题的一般方法，就是将其转化为端点的坐标关系，再根据联立消元后的一元二次方程根与系数的大小关系，构建方程(组)求解.2.弦中点问题的解法【变式训练】设椭圆C：(a>b>0)过点(0，4)，离心率为(1)求椭圆C的方程.(2)求过点(3，0)且斜率为的直线被C所截线段的中点坐标.【变式训练】设椭圆C：(a>b>0)过点(0【解析】(1)将点(0，4)代入C的方程得∴b=4,∴椭圆C的方程为(2)过点(3，0)且斜率为的直线方程为设直线与C的交点为A(x1,y1),B(x2,y2)，将直线方程代入C的方程，得即x2-3x-8=0,解得∴AB的中点的横坐标纵坐标即所截线段的中点坐标为【解析】(1)将点(0，4)代入C的方程得∴b=4考向3探究性、存在性问题【典例3】(2012·福建高考)如图，椭圆E：(a>b>0)的左焦点为F1，右焦点为F2，离心率过F1的直线交椭圆于A，B两点，且△ABF2的周长为8.考向3探究性、存在性问题(1)求椭圆E的方程.(2)设动直线l：y=kx+m与椭圆E有且只有一个公共点P，且与直线x=4相交于点Q.试探究：在坐标平面内是否存在定点M，使得以PQ为直径的圆恒过点M？若存在，求出点M的坐标；若不存在，说明理由.(1)求椭圆E的方程.【思路点拨】(1)利用待定系数法求解，(2)假设存在点M满足题设条件，先探索出M必在x轴上，再根据以PQ为直径的圆恒过M点，即恒成立，求M点横坐标大小，从而判断点Ｍ是否存在.【思路点拨】(1)利用待定系数法求解，(2)假设存在点M满足【规范解答】方法一：(1)因为|AB|+|AF2|+|BF2|=8，即|AF1|+|F1B|+|AF2|+|BF2|=8，又|AF1|+|AF2|=|BF1|+|BF2|=2a,所以4a=8,a=2.又因为所以c=1,所以故椭圆E的方程是【规范解答】方法一：(1)因为|AB|+|AF2|+|BF2(2)由得(4k2+3)x2+8kmx+4m2-12=0.因为动直线l与椭圆E有且只有一个公共点P(x0,y0)，所以m≠0且Δ=0,即64k2m2-4(4k2+3)(4m2-12)=0，化简得4k2-m2+3=0.(*)此时所以(2)由得由得Q(4,4k+m).假设平面内存在定点M满足条件，由图形对称性知，点M必在x轴上.设M(x1,0)，则对满足(*)式的m,k恒成立.因为由得整理，得(**)由得Q(4,4k+m).由于(**)式对满足(*)式的m,k恒成立，所以解得x1=1.故存在定点M(1,0)，使得以PQ为直径的圆恒过点M.方法二：(1)同方法一.(2)由得(4k2+3)x2+8kmx+4m2-12=0.因为动直线l与椭圆E有且只有一个公共点P(x0,y0)，所以m≠0且Δ=0,由于(**)式对满足(*)式的m,k恒成立，所以即64k2m2-4(4k2+3)(4m2-12)=0，化简得4k2-m2+3=0.(*)此时所以由得Q(4,4k+m).假设平面内存在定点M满足条件，由图形对称性知，点M必在x轴上.即64k2m2-4(4k2+3)(4m2-12)=0，取k=0,此时以PQ为直径的圆为(x-2)2+交x轴于点M1(1,0),M2(3,0)；取m=2,此时Q(4,0)，以PQ为直径的圆为交x轴于点M3(1，0)，M4(4,0).所以若符合条件的点M存在，则M的坐标必为(1，0).以下证明M(1，0)就是满足条件的点:因为M的坐标为(1，0)，所以从而故恒有即存在定点M(1，0)，使得以PQ为直径的圆恒过点M.取k=0,此时以P【拓展提升】探究性、存在性问题的求解步骤(1)先假设存在,引入参数,根据题目条件列出关于参数的方程(组)或不等式(组).(2)解此方程(组)或不等式(组),若有解即存在,若无解则不存在.【拓展提升】探究性、存在性问题的求解步骤【变式训练】(2013·宝鸡模拟)已知：向量O为坐标原点，动点M满足：(1)求动点M的轨迹C的方程.(2)已知直线l1,l2都过点B(0,1)，且l1⊥l2，l1,l2与轨迹C分别交于点D,E，试探究是否存在这样的直线使得△BDE是等腰直角三角形.若存在，指出这样的直线共有几组(无需求出直线的方程)；若不存在，请说明理由.【变式训练】(2013·宝鸡模拟)已知：向量【解析】(1)方法一：设则∴动点M的轨迹为以A，A′为焦点，长轴长为4的椭圆.由2a=4，得a=2,∴动点M的轨迹C的方程为方法二:设点M(x,y),则【解析】(1)方法一：设则∴点M的轨迹C是以为焦点，长轴长为4的椭圆.∴动点M的轨迹C的方程为(2)轨迹C是椭圆点B(0,1)是它的上顶点，设满足条件的直线l1，l2存在，由题意知两直线斜率存在且不为零，不妨设直线l1的方程为y=kx+1(k＞0)①则直线l2的方程为②∴点M的轨迹C是以为焦点，长轴长为4的将①代入椭圆方程并整理得：(1+4k2)x2+8kx=0，可得则将②代入椭圆方程并整理得：(4+k2)x2-8kx=0，可得由△BDE是等腰直角三角形得|BD|=|BE|将①代入椭圆方程并整理得：(1+4k2)x2+8kx=0，可k3+4k=1+4k2k3-1=4k2-4k(k-1)(k2+k+1)=4k(k-1)③∴k=1或k2-3k+1=0④∵方程④的判别式Δ=5＞0，即方程④有两个不相等的实根，且不为1.∴方程③有三个互不相等的实根.即满足条件的直线l1，l2存在，共有3组．k3+4k=1+4k2k3-1=4k2-4k【满分指导】解答直线与圆锥曲线位置关系的综合问题【典例】(12分)(2012·北京高考)已知曲线C：(5-m)x2+(m-2)y2=8(m∈R).(1)若曲线C是焦点在x轴上的椭圆，求m的取值范围.(2)设m=4，曲线C与y轴的交点为A，B(点A位于点B的上方)，直线y=kx+4与曲线C交于不同的两点M，N，直线y=1与直线BM交于点G.求证：A，G，N三点共线.【满分指导】解答直线与圆锥曲线位置关系的综合问题【思路点拨】已知条件条件分析曲线C是焦点在x轴上的椭圆构建关于m的不等式组m=4得曲线C：x2+2y2=8直线y=kx+4与曲线C交于不同两点联立消元所得一元二次方程的判别式Δ>0A，G，N三点共线只需证kAN=kAG即可【思路点拨】已知条件条件分析曲线C是焦点在x轴上的椭圆构建关【规范解答】(1)曲线C是焦点在x轴上的椭圆，当且仅当

①

…………3分解得所以m的取值范围是……5分(2)当m=4时，曲线C的方程为x2+2y2=8,点A，B的坐标分别为(0，2)，(0，-2).……………6分由得(1+2k2)x2+16kx+24=0.…7分【规范解答】(1)曲线C是焦点在x轴上的椭圆，当且仅当因为直线与曲线C交于不同的两点，所以

②……8分设点M，N的坐标分别为(x1,y1),(x2,y2),则y1=kx1+4,y2=kx2+4,直线BM的方程为点G的坐标为………9分因为直线AN和直线AG的斜率分别为所以=因为直线与曲线C交于不同的两点，所以

…………11分即kAN=kAG.又AN与AG有公共点A，故A，G，N三点共线.…………………12分………………【失分警示】(下文①②③见规范解答过程)【失分警示】(下文①②③见规范解答过程)1.(2013·咸阳模拟)设抛物线y2=8x的准线与x轴交于点Q，若过点Q的直线l与抛物线有公共点，则直线l的斜率的取值范围是()(A)(B)［-2,2］(C)［-1,1］(D)［-4,4］1.(2013·咸阳模拟)设抛物线y2=8x的准线与x轴交于【解析】选C.由题意得Q(-2，0).设l的方程为y=k(x+2),代入y2=8x得k2x2+4(k2-2)x+4k2=0,∴当k=0时，直线l与抛物线恒有一个交点；当k≠0时,Δ=16(k2-2)2-16k4≥0,即k2≤1,∴-1≤k≤1,且k≠0,综上-1≤k≤1.【解析】选C.由题意得Q(-2，0).设l的方程为y=k(x2.(2013·九江模拟)直线3x-4y+4=0与抛物线x2=4y和圆x2+(y-1)2=1从左到右的交点依次为A，B，C，D.则的值为()(A)16(B)(C)4(D)2.(2013·九江模拟)直线3x-4y+4=0与抛物线x2【解析】选B.由得x2-3x-4=0，∴xA=-1,xD=4，直线3x-4y+4=0恰过抛物线的焦点F(0，1).【解析】选B.由得x2-3x-4=3.(2013·安庆模拟)已知双曲线方程是过定点P(2，1)作直线交双曲线于P1，P2两点，并使P(2，1)为P1P2的中点，则此直线方程是______.3.(2013·安庆模拟)已知双曲线方程是【解析】设点P1(x1,y1),P2(x2,y