等高模型(古柏优讲)课件

等高模型

1科学教育等高模型1科学教育

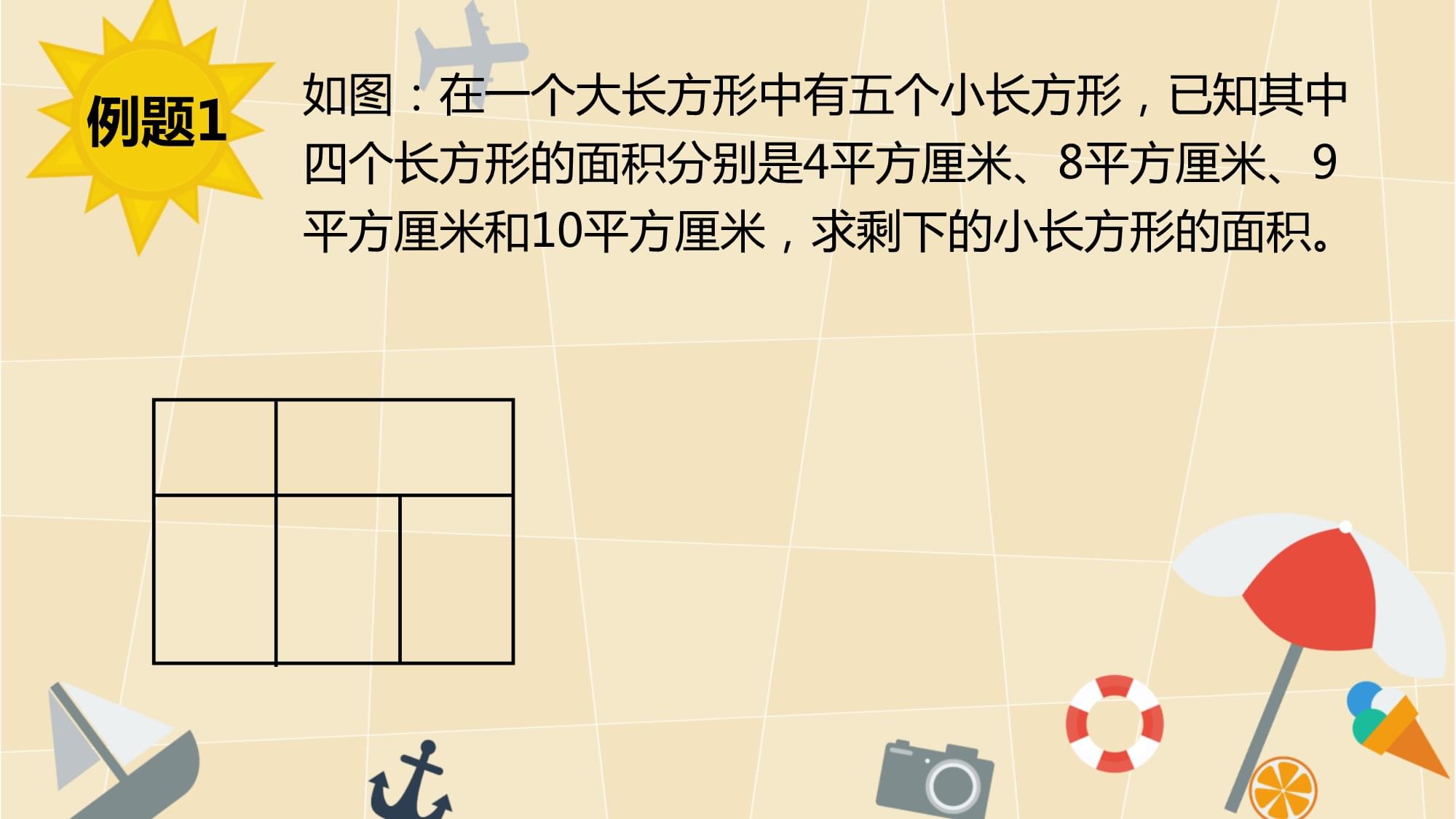
Part1.长方形Part1.长方形如图：在一个大长方形中有五个小长方形，已知其中四个长方形的面积分别是4平方厘米、8平方厘米、9平方厘米和10平方厘米，求剩下的小长方形的面积。例题1如图：在一个大长方形中有五个小长方形，已知其中四个长方形的面如图：在一个大长方形中有五个小长方形，已知其中四个长方形的面积分别是4平方厘米、8平方厘米、9平方厘米和10平方厘米，求剩下的小长方形的面积。例题14cm210cm28cm29cm2ABCDEFG解：给各个顶点上标注字母，如右图。因为长方形AEKI与长方形IKHD的一边重合，S长方形IKHD=2S长方形AEKI所以：HK=2EK所以：S长方KFCH=2S长方形EBFK=2×10=20（cm2）S长方形OFCG=20-9=11cm2HIKO如图：在一个大长方形中有五个小长方形，已知其中四个长方形的面如图：已知一个大长方形中的三个小长方形的面积分别是5平方厘米、7平方厘米和10平方厘米，求剩下的小长方形的面积。练习1如图：已知一个大长方形中的三个小长方形的面积分别是5平方厘如图：已知一个大长方形中的三个小长方形的面积分别是5平方厘米、7平方厘米和10平方厘米，求剩下的小长方形的面积。练习15cm27cm210cm2ABCDEFHIK解：给各个顶点上标注字母，如右图。因为长方形AEKI与长方形IKHD的一边重合所以S长方形IKHD=2S长方形AEKI

HK=2EK

即：S长方形KFCH=2S长方形EBFK=2×7=14（cm2）

如图：已知一个大长方形中的三个小长方形的面积分别是5平方厘

Part2.三角形Part2.三角形等高三角形三角形高不变，底越大，则三角形面积越大等高三角形三角形高不变，底越大，则三角形面积越大等高三角形高不变，底变为原来的2倍2cm2cm2cm4cmS=2×2÷2=2（平方厘米）S=4×2÷2=4（平方厘米）两个三角形高相等面积的倍数关系=底的倍数关系等高三角形高不变，底变为原来的2倍2cm2cm2cm4cmS平行线间三角形一组平行线间，同底的三角形面积相等haS=a×h÷2

一组平行线间的三角形等高。平行线间三角形一组平行线间，同底的三角形面积相等haS=a×如图：已知△ABC的面积是20平方厘米，△ABD的边BD的长为3厘米，△ADC的边CD的长是2厘米，求△ABD的面积。例题2如图：已知△ABC的面积是20平方厘米，△ABD的边B如图：已知△ABC的面积是20平方厘米，△ABD的边BD的长为3厘米，△ADC的边CD的长是2厘米，求△ABD的面积。例题2解：因为BC、BD在同一条直线上，顶点重合所以△ADC、△ABD等高3÷2=1.5BD=1.5DC因为△ABC的面积是20平方厘米所以△ABD的面积：

20÷（1.5+1）×1.5=12（平方厘米）如图：已知△ABC的面积是20平方厘米，△ABD的边B如图：已知在△ABC中，BD的长是3厘米，CD的长是6厘米，且△ABD的面积是9平方厘米，求△ACD的面积。练习2如图：已知在△ABC中，BD的长是3厘米，CD的长是如图：已知在△ABC中，BD的长是3厘米，CD的长是6厘米，且△ABD的面积是9平方厘米，求△ACD的面积。练习2解：因为BD、CD在同一条直线上，△ABD、△ACD顶点重合，所以△ABD、△ACD等高。

6÷3=2DC=2BD所以S△ACD=2S△ABD=2×9=18（平方厘米）如图：已知在△ABC中，BD的长是3厘米，CD的长是如图：△ABC的面积是12平方厘米，其中AE=3AB，BD=2BC，则△BDE的面积是多少平方厘米？例题3如图：△ABC的面积是12平方厘米，其中AE=3AB，如图：△ABC的面积是12平方厘米，其中AE=3AB，BD=2BC，则△BDE的面积是多少平方厘米？例题3解：连接AD因为△ACD、△ABC等底，BD=2BC

BC=CD，所以S△ABC=S△ACD=12（cm2）

因为△BDE、△ABD等高，且AE=3AB

BE=2AB，所以

S△BDE=2S△ABD=2×(12+12)=48（cm2）如图：△ABC的面积是12平方厘米，其中AE=3AB，如图：已知△ABC的面积是60平方厘米，点D是边BC的中点，AD=3AE，求△ABE的面积。练习3如图：已知△ABC的面积是60平方厘米，点D是边BC解：S△ABE=1（份）因为AE、AD在一条直线上，△ABD、△ABE的顶点重合所以△EBD、△ABE等高，AD=3AE

DE=2AE，所以S△EBD=2S△ABE=1×2=2（份）因为BD、BC在一条直线上，△ABD、△ABC的顶点重合，所以△ABD、△ADC等高又因为D是边BC的中点，BD=DC所以S△ABD:S△ADC=1+2=3（份） 1+2+3=6（份）所以△ABE的面积：60÷6=10（cm2）练习3解：S△ABE=1（份）练习3如图：已知△ABC的面积是120平方厘米，点D是边BC的中点，AD=3AE，BE=2BF。△AEF的面积是多少平方厘米？例题4如图：已知△ABC的面积是120平方厘米，点D是边B如图：已知△ABC的面积是120平方厘米，点D是边BC的中点，AD=3AE，BE=2BF。△AEF的面积是多少平方厘米？例题4解：S△AEF=1（份）

△ABF、△AFE等高，BE=2BF

BF=EF，所以S△AFE=S△ABF=1（份）△BED、△ABE等高，AD=3AEDE=2AE，所以S△EBD=2S△ABE=2×(1+1)=4（份）△ABD、△ADC等高，D是边BC的中点

BD=DC，所以S△ABD=S△ADC=1+1+4=6（份）

1+1+4+6=12（份）120÷12=10（cm2）

△AEF的面积是10平方厘米。如图：已知△ABC的面积是120平方厘米，点D是边B如图：在△ABC中，点D、E、F分别是BC、AC、DE的中点，△ABC的面积是1000平方厘米，那么阴影部分的面积是多少平方厘米？练习4如图：在△ABC中，点D、E、F分别是BC、AC、DE如图：在△ABC中，点D、E、F分别是BC、AC、DE的中点，△ABC的面积是1000平方厘米，那么阴影部分的面积是多少平方厘米？练习4解：S△ADF=1（份）△ADF、△AEF等高，点F是边ED的中点

DF=EF，所以S△ADF=S△AEF=1（份）△ACD、△CDE等高，点E是边AC的中点

AE=EC，所以S△CDE=S△AED=1+1=2（份）△ABD、△ACD等高，点D是边BC的中点

BD=CD，所以S△ABD=S△ADC=1+1+2=4（份）

1+1+2+4=8（份）1000÷8=125（cm2）如图：在△ABC中，点D、E、F分别是BC、AC、DE如图：已知在△AEF中，点C是边AE的中点，点B、D是边AF的三等分点，△EDF的面积是50平方厘米，求△ABC的面积。例题5如图：已知在△AEF中，点C是边AE的中点，点B、D如图：已知在△AEF中，点C是边AE的中点，点B、D是边AF的三等分点，△EDF的面积是50平方厘米，求△ABC的面积。例题5解：S△ACB=1（份）

△ABC、△BDC等高，因为点B、D是边AF的三等分点，AB=BD=DF。所以S△DBC=S△ABC=1（份）

△ADC、△EDC等高，点C是边AE的中点

AC=CE，S△EDC=S△ADC=1+1=2（份）

△ADE、△DEF等高，2AD=DF。

S△DEF=S△ADE÷2=（1+1+2）÷2=2（份）

50÷2=25（平方厘米）

△ABC的面积为25平方厘米。如图：已知在△AEF中，点C是边AE的中点，点B、D如图：已知在△AEF中，点D是边AF的中点，点C是边AE的中点，点B是边AD的中点，△ABC的面积是2平方厘米，求△AEF的面积。练习5如图：已知在△AEF中，点D是边AF的中点，点C是边如图：已知在△AEF中，点D是边AF的中点，点C是边AE的中点，点B是边AD的中点，△ABC的面积是2平方厘米，求△AEF的面积。练习5解：1+1+2+4=8（份）8×2=16（平方厘米）如图：已知在△AEF中，点D是边AF的中点，点C是边

Part3.综合题目Part3.综合题目如图：已知长方形ABCD的面积是30平方厘米，△CDE的面积是10平方厘米，对角线AC的长是9厘米，求AE的长。例题6如图：已知长方形ABCD的面积是30平方厘米，△CDE如图：已知长方形ABCD的面积是30平方厘米，△CDE的面积是10平方厘米，对角线AC的长是9厘米，求AE的长。例题6解：由一半模型可得：

S△ACD=30÷2=15（平方厘米）

S△AED=15-10=5（平方厘米）△AED、△CDE等高

S△CDE=2S△ACD

CE=2AE所以AE=9÷(1+2)=3（厘米）如图：已知长方形ABCD的面积是30平方厘米，△CDE如图：已知长方形ABCD的面积是20平方厘米，△ADE的面积是2平方厘米，边BC的长是4厘米，求EC的长。练习6如图：已知长方形ABCD的面积是20平方厘米，△ADE如图：已知长方形ABCD的面积是20平方厘米，△ADE的面积是2平方厘米，边BC的长是4厘米，求EC的长。练习6解：因为长方形ABCD的面积是20平方厘米，边BC的长是4厘米所以CD=20÷4=5（厘米）由一半模型可得：

S△ACD=20÷2=10（平方厘米）

S△AEC=10-2=8（平方厘米）△AED、△ACE等高

S△ACE=4S△ADE所以CE=4DE

所以DE=5÷(4+1)=1（厘米）所以EC=5-1=4（厘米）如图：已知长方形ABCD的面积是20平方厘米，△ADE总结三角形底相等，面积的倍数关系等于高的倍数关系三角形高相等，面积的倍数关系等于底的倍数关系一组平行线间，等底的三角形面积相等借助辅助线构造等高模型总结三角形底相等，面积的倍数关系等于高的倍数关系谢谢!谢谢!等高模型

34科学教育等高模型1科学教育

Part1.长方形Part1.长方形如图：在一个大长方形中有五个小长方形，已知其中四个长方形的面积分别是4平方厘米、8平方厘米、9平方厘米和10平方厘米，求剩下的小长方形的面积。例题1如图：在一个大长方形中有五个小长方形，已知其中四个长方形的面如图：在一个大长方形中有五个小长方形，已知其中四个长方形的面积分别是4平方厘米、8平方厘米、9平方厘米和10平方厘米，求剩下的小长方形的面积。例题14cm210cm28cm29cm2ABCDEFG解：给各个顶点上标注字母，如右图。因为长方形AEKI与长方形IKHD的一边重合，S长方形IKHD=2S长方形AEKI所以：HK=2EK所以：S长方KFCH=2S长方形EBFK=2×10=20（cm2）S长方形OFCG=20-9=11cm2HIKO如图：在一个大长方形中有五个小长方形，已知其中四个长方形的面如图：已知一个大长方形中的三个小长方形的面积分别是5平方厘米、7平方厘米和10平方厘米，求剩下的小长方形的面积。练习1如图：已知一个大长方形中的三个小长方形的面积分别是5平方厘如图：已知一个大长方形中的三个小长方形的面积分别是5平方厘米、7平方厘米和10平方厘米，求剩下的小长方形的面积。练习15cm27cm210cm2ABCDEFHIK解：给各个顶点上标注字母，如右图。因为长方形AEKI与长方形IKHD的一边重合所以S长方形IKHD=2S长方形AEKI

HK=2EK

即：S长方形KFCH=2S长方形EBFK=2×7=14（cm2）

如图：已知一个大长方形中的三个小长方形的面积分别是5平方厘

Part2.三角形Part2.三角形等高三角形三角形高不变，底越大，则三角形面积越大等高三角形三角形高不变，底越大，则三角形面积越大等高三角形高不变，底变为原来的2倍2cm2cm2cm4cmS=2×2÷2=2（平方厘米）S=4×2÷2=4（平方厘米）两个三角形高相等面积的倍数关系=底的倍数关系等高三角形高不变，底变为原来的2倍2cm2cm2cm4cmS平行线间三角形一组平行线间，同底的三角形面积相等haS=a×h÷2

一组平行线间的三角形等高。平行线间三角形一组平行线间，同底的三角形面积相等haS=a×如图：已知△ABC的面积是20平方厘米，△ABD的边BD的长为3厘米，△ADC的边CD的长是2厘米，求△ABD的面积。例题2如图：已知△ABC的面积是20平方厘米，△ABD的边B如图：已知△ABC的面积是20平方厘米，△ABD的边BD的长为3厘米，△ADC的边CD的长是2厘米，求△ABD的面积。例题2解：因为BC、BD在同一条直线上，顶点重合所以△ADC、△ABD等高3÷2=1.5BD=1.5DC因为△ABC的面积是20平方厘米所以△ABD的面积：

20÷（1.5+1）×1.5=12（平方厘米）如图：已知△ABC的面积是20平方厘米，△ABD的边B如图：已知在△ABC中，BD的长是3厘米，CD的长是6厘米，且△ABD的面积是9平方厘米，求△ACD的面积。练习2如图：已知在△ABC中，BD的长是3厘米，CD的长是如图：已知在△ABC中，BD的长是3厘米，CD的长是6厘米，且△ABD的面积是9平方厘米，求△ACD的面积。练习2解：因为BD、CD在同一条直线上，△ABD、△ACD顶点重合，所以△ABD、△ACD等高。

6÷3=2DC=2BD所以S△ACD=2S△ABD=2×9=18（平方厘米）如图：已知在△ABC中，BD的长是3厘米，CD的长是如图：△ABC的面积是12平方厘米，其中AE=3AB，BD=2BC，则△BDE的面积是多少平方厘米？例题3如图：△ABC的面积是12平方厘米，其中AE=3AB，如图：△ABC的面积是12平方厘米，其中AE=3AB，BD=2BC，则△BDE的面积是多少平方厘米？例题3解：连接AD因为△ACD、△ABC等底，BD=2BC

BC=CD，所以S△ABC=S△ACD=12（cm2）

因为△BDE、△ABD等高，且AE=3AB

BE=2AB，所以

S△BDE=2S△ABD=2×(12+12)=48（cm2）如图：△ABC的面积是12平方厘米，其中AE=3AB，如图：已知△ABC的面积是60平方厘米，点D是边BC的中点，AD=3AE，求△ABE的面积。练习3如图：已知△ABC的面积是60平方厘米，点D是边BC解：S△ABE=1（份）因为AE、AD在一条直线上，△ABD、△ABE的顶点重合所以△EBD、△ABE等高，AD=3AE

DE=2AE，所以S△EBD=2S△ABE=1×2=2（份）因为BD、BC在一条直线上，△ABD、△ABC的顶点重合，所以△ABD、△ADC等高又因为D是边BC的中点，BD=DC所以S△ABD:S△ADC=1+2=3（份） 1+2+3=6（份）所以△ABE的面积：60÷6=10（cm2）练习3解：S△ABE=1（份）练习3如图：已知△ABC的面积是120平方厘米，点D是边BC的中点，AD=3AE，BE=2BF。△AEF的面积是多少平方厘米？例题4如图：已知△ABC的面积是120平方厘米，点D是边B如图：已知△ABC的面积是120平方厘米，点D是边BC的中点，AD=3AE，BE=2BF。△AEF的面积是多少平方厘米？例题4解：S△AEF=1（份）

△ABF、△AFE等高，BE=2BF

BF=EF，所以S△AFE=S△ABF=1（份）△BED、△ABE等高，AD=3AEDE=2AE，所以S△EBD=2S△ABE=2×(1+1)=4（份）△ABD、△ADC等高，D是边BC的中点

BD=DC，所以S△ABD=S△ADC=1+1+4=6（份）

1+1+4+6=12（份）120÷12=10（cm2）

△AEF的面积是10平方厘米。如图：已知△ABC的面积是120平方厘米，点D是边B如图：在△ABC中，点D、E、F分别是BC、AC、DE的中点，△ABC的面积是1000平方厘米，那么阴影部分的面积是多少平方厘米？练习4如图：在△ABC中，点D、E、F分别是BC、AC、DE如图：在△ABC中，点D、E、F分别是BC、AC、DE的中点，△ABC的面积是1000平方厘米，那么阴影部分的面积是多少平方厘米？练习4解：S△ADF=1（份）△ADF、△AEF等高，点F是边ED的中点

DF=EF，所以S△ADF=S△AEF=1（份）△ACD、△CDE等高，点E是边AC的中点

AE=EC，所以S△CDE=S△AED=1+1=2（份）△ABD、△ACD等高，点D是边BC的中点

BD=CD，所以S△ABD=S△ADC=1+1+2=4（份）

1+1+2+4=8（份）1000÷8=125（cm2）如图：在△ABC中，点D、E、F分别是BC、AC、DE如图：已知在△AEF中，点C是边AE的中点，点B、D是边AF的三等分点，△EDF的面积是50平方厘米，求△ABC的面积。例题5如图：已知在△AEF中，点C是边AE的中点，点B、D如图：已知在△AEF中，点C是边AE的中点，点B、D是边AF的三等分点，△EDF的面积是50平方厘米，求△ABC的面积。例题5解：S△ACB=1（份）

△ABC、△BDC等高，因为点B、D是边AF的三等分点，AB=BD=DF。所以S△DBC=S△ABC=1（份）

△ADC、△EDC等高，点C是边AE的中点

AC=CE，S△EDC=S△ADC=1+1=2（份）

△ADE、△DEF等高，2AD=DF。

S△DEF=S△ADE÷2=（1+1+2）÷2=2（份）

50÷2=25（平方厘米）

△ABC的面积为25平方厘米。如图：已知在△AEF中，点C是边AE的中点，点B、D如图：已知在△AEF中，点D是边AF的中点，点C是边AE的中点，点B是边AD的中点，△ABC的面积是2平方厘米，求△AEF的面积。练习5如图：已知在△AEF中，点D是边AF的中点，点C是边如图：已知在△AEF中，点D是边AF