2022年高考数学基础知识综合复习第22讲概率课件

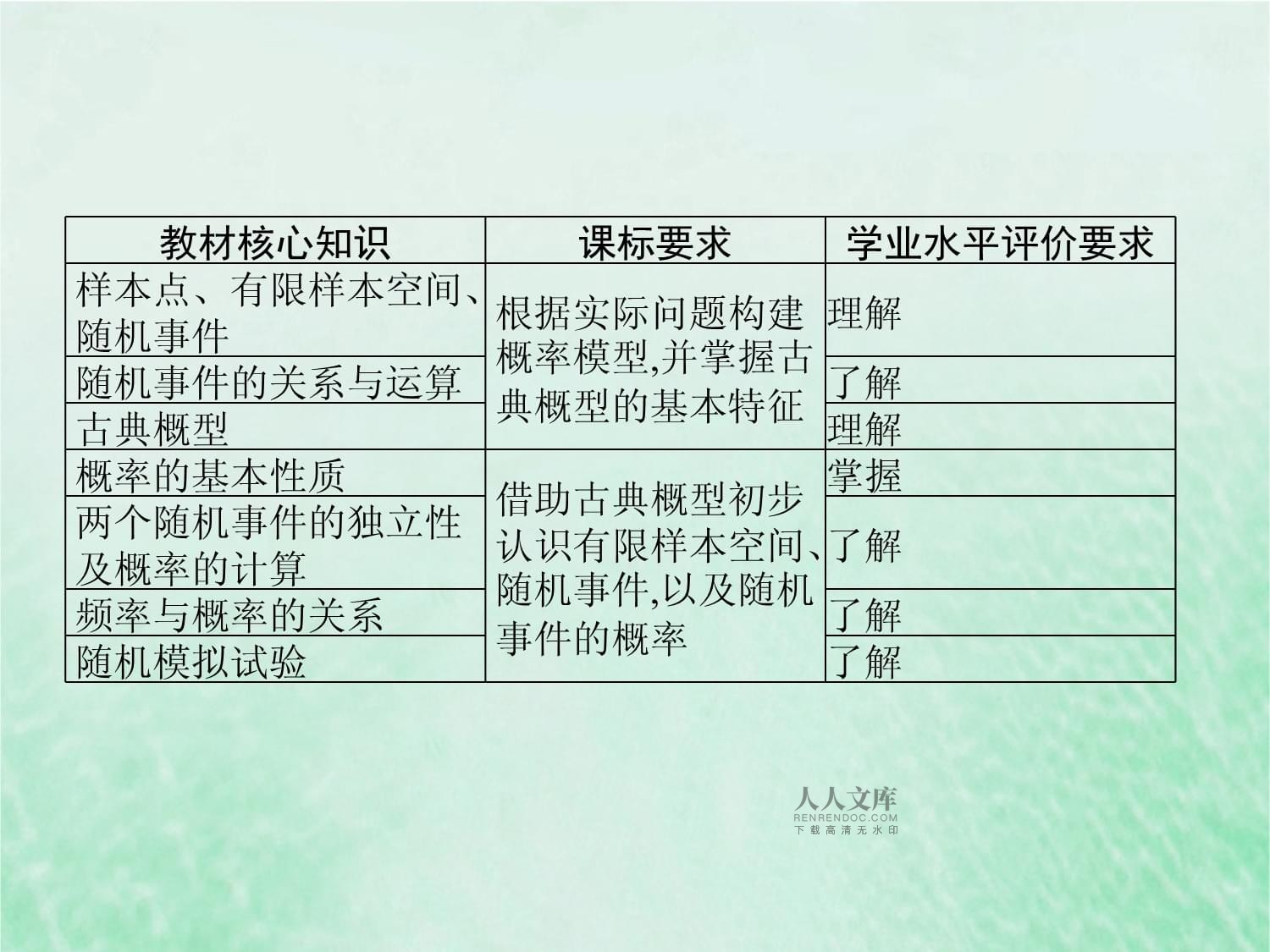
1、第22讲概率教材核心知识课标要求学业水平评价要求样本点、有限样本空间、随机事件根据实际问题构建概率模型,并掌握古典概型的基本特征理解随机事件的关系与运算了解古典概型理解概率的基本性质借助古典概型初步认识有限样本空间、随机事件,以及随机事件的概率掌握两个随机事件的独立性及概率的计算了解频率与概率的关系了解随机模拟试验了解1.随机事件和确定事件(1)在条件S下,一定会发生的事件叫作相对于条件S的必然事件.(2)在条件S下,一定不会发生的事件叫作相对于条件S的不可能事件.(3)必然事件与不可能事件统称为确定事件.(4)在条件S下可能发生也可能不发生的事件,叫作随机事件.(5)确定事件和随机事件统称为

2、事件,一般用大写字母A,B,C,表示.2.频率与概率(1)在相同的条件S下重复n次试验,观察某一事件A是否出现,称n次试验中事件A出现的次数nA为事件A出现的频数,称事件A出现的比例fn(A)= 为事件A出现的频率.(2)对于给定的随机事件A,如果随着试验次数的增加,事件A发生的频率fn(A)稳定在某个常数上,把这个常数记作P(A),称为事件A的概率,简称为A的概率.3.互斥事件与对立事件(1)互斥事件:若AB为不可能事件(AB=),则称事件A与事件B互斥,其含义是:事件A与事件B在任何一次试验中不会同时发生.(2)对立事件:若AB为不可能事件,而AB为必然事件,那么事件A与事件B互为对立事件

3、,其含义是:事件A与事件B在任何一次试验中有且仅有一个发生.4.概率的几个基本性质(1)概率的取值范围:0P(A)1.(2)必然事件的概率:P(A)=1.(3)不可能事件的概率:P(A)=0.(4)互斥事件的概率加法公式:P(AB)=P(A)+P(B)(A,B互斥).P(A1A2An)=P(A1)+P(A2)+P(An)(A1,A2,An彼此互斥).(5)对立事件的概率:P( )=1-P(A).5.基本事件的特点(1)任何两个基本事件是互斥的.(2)任何事件(除不可能事件)都可以表示成基本事件的和.6.古典概型具有以下两个特点的概率模型称为古典概率模型,简称古典概型.(1)试验中所有可能出现的

4、基本事件只有有限个.(2)每个基本事件出现的可能性相等.7.古典概型的概率公式 考点一考点二考点三随机事件与概率角度1.事件的关系与运算例1在10个学生中,男生有x个,现从10个学生中任选6人去参加某项活动:至少有一个女生;5个男生,1个女生;3个男生,3个女生.若要使为必然事件、为不可能事件、为随机事件,则x为()A.5B.6C.3或4D.5或6答案 C解析 由题意知,10名同学中,男生人数少于5人,但不少于3人,x=3或x=4.考点一考点二考点三掌握必然事件、不可能事件、随机事件的不同点.考点一考点二考点三角度2.互斥与对立事件例2把红、黄、蓝、白4张纸牌随机分给甲、乙、丙、丁4个人,每人

5、分得一张,事件“甲分得红牌”与事件“乙分得红牌”是()A.对立事件B.互斥但不对立事件C.不可能事件D.以上都不对考点一考点二考点三答案 B 解析 把红、蓝、黑、白四张纸牌随机分给甲、乙、丙、丁四个人,事件“甲分得红牌”与“乙分得红牌”不会同时发生,则两者是互斥事件,但除了“甲分得红牌”与“乙分得红牌”之外,还有“丙分得红牌”和“丁分得红牌”,则两者不是对立事件,事件“甲分得红牌”与“乙分得红牌”是互斥但不对立事件.考点一考点二考点三对立事件与互斥事件的联系. 考点一考点二考点三例3某小组有3名男生和2名女生,从中任选2名同学参加演讲比赛,判断下列每对事件是不是互斥事件?是不是对立事件?(1)

6、“恰有1名男生”与“恰有2名男生”;(2)“至少有1名男生”与“全是男生”;(3)“至少有1名男生”与“全是女生”;(4)“至少有1名男生”与“至少有1名女生”.其中互为互斥事件的是,互为对立事件的是.考点一考点二考点三答案 (1)(3)(3) 解析 (1)“恰有1名男生”与“恰有2名男生”不能同时发生,但能同时不发生,是互斥事件,但不是对立事件;(2)“至少有1名男生”与“全是男生”能同时发生,不是互斥事件;(3)“至少有1名男生”与“全是女生”不能同时发生,也不能同时不发生,既是互斥事件,又是对立事件;(4)“至少有1名男生”与“至少有1名女生”能同时发生,不是互斥事件.考点一考点二考点三

7、对立事件与互斥事件的异同. 考点一考点二考点三角度4.古典概型的概率计算例4从装有3个红球、2个白球的袋中任取3个球,则所取的3个球中至少有1个白球的概率是()答案 D 解析 由题意可知从5个球中任取3个球的所有情况有10种,所取的3个球至少有1个白球的情况有(10-1)种,根据古典概型公式得所求概率P= .考点一考点二考点三事件的相互独立性例5下列各对事件中,不互为相互独立事件的是()A.掷一枚骰子一次,事件M“出现偶数点”;事件N“出现3点或6点”B.袋中有3白、2黑共5个大小相同的小球,依次有放回地摸两球,事件M“第一次摸到白球”,事件N“第二次摸到白球”C.袋中有3白、2黑共5个大小相

8、同的小球,依次不放回地摸两球,事件M“第一次摸到白球”,事件N“第二次摸到黑球”D.甲组3名男生,2名女生;乙组2名男生,3名女生,现从甲、乙两组中各选1名同学参加演讲比赛,事件M“从甲组中选出1名男生”,事件N“从乙组中选出1名女生”考点一考点二考点三答案 C 解析 根据事件的特点易知,事件M是否发生对事情N发生的概率没有影响,故M与N是相互独立事件,故A,B,D属于相互独立事件.对于C:由于第一次摸到球不放回,因此会对第二次摸到球的概率产生影响,所以这两个事件不是相互独立事件.考点一考点二考点三把握相互独立事件的概念与判断. 考点一考点二考点三频率与概率角度1.频率与概率的关系及概率的意义例6已知某人在投篮时投中的概率为50%,则下列说法正确的是()A.若他投100次,一定有50次投中B.若他投一次,一定投中C.他投一次投中的可能性大小为50%D.以上说法均错答案 C解析 概率是指一件事情发生的可能性大小.