学习数字信号处理dsp讲义

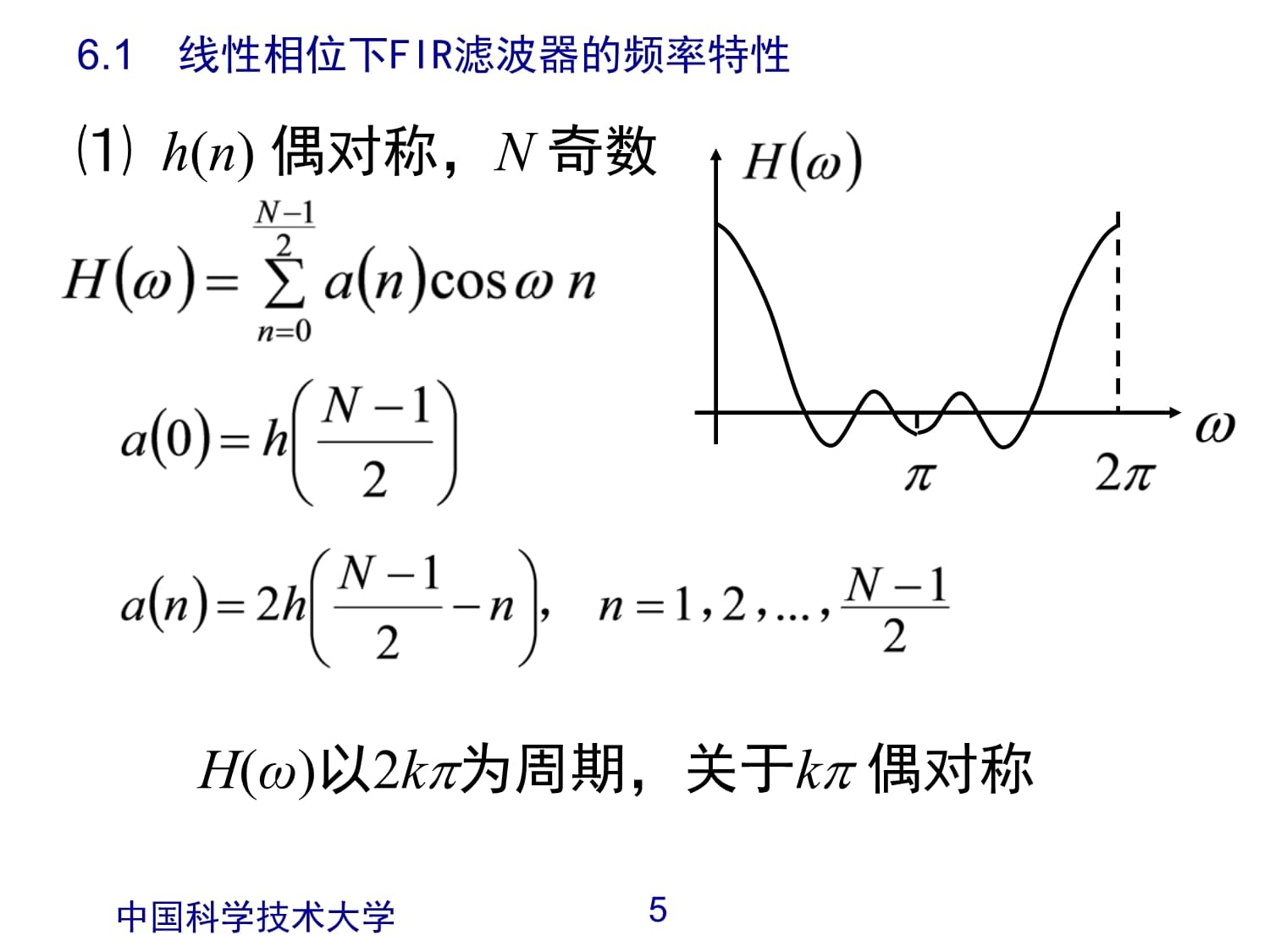
1、中国科学技术大学16 FIR数字滤波器设计中国科学技术大学26.1 线性相位下FIR滤波器的频率特性中国科学技术大学36.1 线性相位下FIR滤波器的频率特性在线性相位条件下，（偶对称） （奇对称）群延迟均为中国科学技术大学4滤波器幅度响应6.1 线性相位下FIR滤波器的频率特性4种情况：中国科学技术大学5 h(n) 偶对称，N 奇数6.1 线性相位下FIR滤波器的频率特性H()以2k为周期，关于k 偶对称中国科学技术大学66.1 线性相位下FIR滤波器的频率特性中国科学技术大学76.1 线性相位下FIR滤波器的频率特性 h(n) 偶对称，N 偶数H()以4k为周期关于2k 偶对称，关于(2k

2、+1) 奇对称H(2k+1) =0，不能用来逼近高通中国科学技术大学86.1 线性相位下FIR滤波器的频率特性中国科学技术大学96.1 线性相位下FIR滤波器的频率特性 h(n) 奇对称，N 奇数必有H(k)=0，可逼近带通H()以2k为周期，关于k 奇对称中国科学技术大学106.1 线性相位下FIR滤波器的频率特性中国科学技术大学116.1 线性相位下FIR滤波器的频率特性 h(n) 奇对称，N 偶数H()以4k为周期关于2k 奇对称，关于(2k+1) 偶对称H(2k)=0，不能用来逼近低通中国科学技术大学126.1 线性相位下FIR滤波器的频率特性中国科学技术大学136.2 傅立叶级数法设

3、计FIR滤波器（窗函数法）中国科学技术大学146.2 傅立叶级数法设计FIR滤波器（窗函数法）一、基本设计方法对 hd(n) 截取有限个值形成h(n)给定Hd(ej)导出hd(n)故， H(ej)对Hd(ej)的逼近程度随截取长度而增加因基于频域特性的解析表达与窗函数中国科学技术大学15理想低通的逼近6.2 傅立叶级数法设计FIR滤波器（窗函数法）n中国科学技术大学16为构造一个物理可实现的，长度为 N 的 FIR， 把hd(n)移动 个采样点（设N为奇数） 截取N个点，得到矩形窗即6.2 傅立叶级数法设计FIR滤波器（窗函数法）中国科学技术大学17nnN-16.2 傅立叶级数法设计FIR滤波

4、器（窗函数法）中国科学技术大学18h(n)的频率响应，频域卷积6.2 傅立叶级数法设计FIR滤波器（窗函数法）中国科学技术大学19过冲6.2 傅立叶级数法设计FIR滤波器（窗函数法）中国科学技术大学20 因为截短，产生过渡带，宽度为窗函数的主瓣宽度。对矩形窗， 增加N，可使过渡带变得陡峭，但对一个固定的窗函数不能改变肩峰值大小。 Gibbs效应。6.2 傅立叶级数法设计FIR滤波器（窗函数法）中国科学技术大学216.2 傅立叶级数法设计FIR滤波器（窗函数法）中国科学技术大学22二、窗函数的选择过渡带的宽度：与窗函数的主瓣宽度有关肩峰值大小：与窗函数的旁瓣大小有关选择窗函数的原则： 主瓣窄，使

5、过渡带陡峭 旁瓣低，减小肩峰和余振6.2 傅立叶级数法设计FIR滤波器（窗函数法）中国科学技术大学23 过渡带与肩峰值的折中处理 或增加系统复杂度，两者同时改善 选择低旁瓣窗函数，大的止带衰减。 选择大的 N ， 控制过渡区宽度 选择对称的窗函数，可设计线性相位 FIR 6.2 傅立叶级数法设计FIR滤波器（窗函数法）中国科学技术大学24 主瓣 旁瓣 最小阻带衰减矩形 4/N -13dB -21dB三角 8/N -25 -25Hanning 8/N -32 -44Hamming 8/N -42 -53Blackman 12/N -57 -74 6.2 傅立叶级数法设计FIR滤波器（窗函数法）常

6、用窗函数中国科学技术大学256.2 傅立叶级数法设计FIR滤波器（窗函数法）Hamming窗，低通中国科学技术大学266.2 傅立叶级数法设计FIR滤波器（窗函数法）Blackman窗，带通中国科学技术大学276.2 傅立叶级数法设计FIR滤波器（窗函数法）Kaiser窗，带阻中国科学技术大学286.3 频率抽样设计方法中国科学技术大学296.3 频率抽样设计方法一、基本方法DFT法基于频域取样定理给定频率响应Hd(ej) ，进行等间距取样，则或中国科学技术大学30二、频率响应的逼近6.3 频率抽样设计方法频率响应的解析表达频率取样与内插函数的组合 H(K)对内插函数加权中国科学技术大学316

7、.3 频率抽样设计方法理想低通滤波器频域取样：02，N330.520.52中国科学技术大学326.3 频率抽样设计方法问题：对应于取样点的频率，衰减无穷大 取样点外，最小衰减不足20 dB中国科学技术大学33形式上： 取样点之间的频率响应通过内插函数得到原理上： 理想低通的冲激响应序列在时域上无限长无论 N 多大，也不能满足频域取样定理6.3 频率抽样设计方法中国科学技术大学34改进思路：修改|Hd(ej)|，展宽过渡带，设置非零点6.3 频率抽样设计方法0.5中国科学技术大学35改进后的频率响应止带最小衰减 20 dB6.3 频率抽样设计方法过渡带展宽1倍，至中国科学技术大学36改进后形式上

8、：增加了非零点取样，抵消通带内的内插函数原理上：修改后的|Hd(ej)|，频率变化减弱，时域序列能量随时间减少6.3 频率抽样设计方法中国科学技术大学37三、优化考虑1）增加过渡带非零点取样点，改善止带衰减特性 提高取样点数（增加 N），压缩过渡带过渡带非零点过渡带宽止带衰减无20 dB150 dB270 dB6.3 频率抽样设计方法中国科学技术大学382）优化非零点取值选择H1，H2，使6.3 频率抽样设计方法通带止带中国科学技术大学39H1与H2分别是对应频率点内插函数的系数H(ej)是H1，H2的线性函数设Hd(ej)是低通，通带至第M-1个采样点截止则6.3 频率抽样设计方法中国科学技

9、术大学406.3 频率抽样设计方法中国科学技术大学416.3 频率抽样设计方法2H1H1H2H2中国科学技术大学426.3 频率抽样设计方法低通滤波器：p=0.2， s=0.3， 50dB中国科学技术大学436.3 频率抽样设计方法过渡带1点展宽，未优化中国科学技术大学446.3 频率抽样设计方法过渡带1点展宽，优化中国科学技术大学456.3 频率抽样设计方法过渡带2点展宽，未优化中国科学技术大学466.3 频率抽样设计方法过渡带2点展宽，优化中国科学技术大学476.4 FIR滤波器的等波纹逼近中国科学技术大学486.4 FIR滤波器的等波纹逼近一、基本原理幅度响应优化设计： 带内误差最少 过

10、渡带最窄 系统阶数最低在通带和止带内分别进行等波纹逼近，最大误差极小化中国科学技术大学496.4 FIR滤波器的等波纹逼近中国科学技术大学50在我看来，Butterworth比Chebyshev整洁，不论从极点分布还是从幅度响应上。但是Chebyshev滤波器虽然长得不是那么帅，有其优势：也就是在平坦性，过度带宽度，复杂度与参数数量上寻找了一个令人满意的折衷点。平坦性差一点，参数多一个，但是能让性能保持不差，但是过渡带与阶数可以改善。而且基本上是做到了“竭尽所能”，为什么这么说呢，在波动带里面，几乎是用足了每一点点允许波动的空间（等幅波动），参数也只多一个，最终等待机会来了一个大跳跃直降谷底。

11、从这一点来看，Chebyshev滤波器似乎比Butterworth更精明一点：Butterworth追求完美，而Chebyshev放弃完美换来了整体的优势。 来自你们同学的评论中国科学技术大学516.4 FIR滤波器的等波纹逼近线性相位FIR滤波器幅度特性的一般表达：P()表达为r个余弦谐波函数之和，中国科学技术大学52h(n)对称性N奇偶性Q()P()偶对称奇数1偶对称偶数奇对称奇数奇对称偶数线性相位4种情况下 Q()与P()的定义中国科学技术大学53设计目标使加权逼近误差函数为等波纹，Chebyshev 逼近这里，6.4 FIR滤波器的等波纹逼近选择一组系数 使中国科学技术大学546.4

12、FIR滤波器的等波纹逼近解的存在性：交替定理P()是 的Chebyshev逼近的充要条件：E()在 中，至少有r+1的极值点i，i=1，2，.，r+1，使r 是用于逼近的余弦谐波函数的个数中国科学技术大学55 E()的极值由两部分组成： H()的极值点 E()独有的极值点，H()的频率边界点6.4 FIR滤波器的等波纹逼近H()的极值点H()的频率边界点中国科学技术大学566.4 FIR滤波器的等波纹逼近极值点分析：4 种线性相位 FIR 滤波器h(n)对称性N奇偶性H()的余弦个数极点数Ne偶对称奇数 偶对称偶数 奇对称奇数 奇对称偶数 中国科学技术大学57结论：若 H() 是由 r 个余弦

13、函数组成，则最多提供 r 个极点交替定理要求 r 个余弦函数和至少有r+1个极点r 个可能极点由 H() 提供，其余极点由 E() 提供幅度值每变换一次，在边界上能提供 2 个极值点特别地，E()取满它所有可能有的极点数目时：最多波纹滤波器（超波纹滤波器）设计6.4 FIR滤波器的等波纹逼近中国科学技术大学58带通误差函数 E() 提供 4 个边界极点6.4 FIR滤波器的等波纹逼近中国科学技术大学59二、最多波纹滤波器设计以低通滤波器为例系统阶数 N 通带起伏 1 止带起伏 2 通带截止频率c 止带起始频率s 6.4 FIR滤波器的等波纹逼近截止频率c ，止带起始频率s不易精确实现中国科学技

14、术大学60h(n) 偶对称，N 奇数最多波纹设计，误差函数 E() 有 个极值其中 H() 取满 个极值6.4 FIR滤波器的等波纹逼近H()cs中国科学技术大学61极值点分配通带止带截止频率c的与止带频率s的顺序位置：6.4 FIR滤波器的等波纹逼近中国科学技术大学62逼近方程（ ）个通带止带6.4 FIR滤波器的等波纹逼近中国科学技术大学636.4 FIR滤波器的等波纹逼近 c，s不是H()的极值点；其余 -2个极值点方程：中国科学技术大学646.4 FIR滤波器的等波纹逼近通带止带中国科学技术大学65N+1个未知数，解法1，用数值迭代法，求解非线性方程组，解出 ，得到最优逼近的滤波器解法

15、2，Lagrange 多项式内插，避免非线性方程求解，用 Lagrange 多项式逼近 ，求各极值点，解出N+1个非线性方程中国科学技术大学66最多波纹法优化的意义：指标 N，1 和2按要求实现调整c与s的位置，过渡带宽优化， 最窄 c与s不要求精确实现6.4 FIR滤波器的等波纹逼近中国科学技术大学676.4 FIR滤波器的等波纹逼近c sc sH()H()中国科学技术大学68三、Remez交换算法设计条件：滤波器阶数N，边界频率 c，s， 频带权重W()原理：通带、止带等波纹逼近目标：以多项式近似 确定极值频率点系统函数6.4 FIR滤波器的等波纹逼近中国科学技术大学696.4 FIR滤波

16、器的等波纹逼近误差方程极值点数 r 由滤波器阶数 N 决定在极值点上的误差k=0，1，r中国科学技术大学70算法过程： 极值频率点初值：均匀分布6.4 FIR滤波器的等波纹逼近通带止带中国科学技术大学716.4 FIR滤波器的等波纹逼近形成关于P()的多项式内插公式和逼近误差中国科学技术大学726.4 FIR滤波器的等波纹逼近在密集的频率点上计算误差公式其中P()为多项式内插公式若有频率点j 使得 |E(j)|则选取j 作为新的极值频率点，返回 直至极值频率收敛，迭代完成迭代过程中， 与 保持不变 根据多项式内插公式P()求出a(n) a）IDFT；b）求解线性方程中国科学技术大学73四、算法讨论1）Remez算法处理不要求=0, 为极值点 不是最多波纹滤波器2）对给定的N，c，s及W()，将有一个最小的、不可事先设置的等波纹逼近误差 过渡带 s-c，事先确定，可设置3）通带与止带间的误差分配由权重W()调节6.4 FIR滤波器的等波纹逼近通带波纹K止带波纹中国科学技术大学744）限定条件下的优化 滤波器阶数N，带内误差，过渡带 最多波纹算法带内误差与 N 给定，算法选择过渡带，使之最窄 Remez算法过渡带与 N 给定，算法选择带内误差，使之最小 其他算法误差与过渡带同时给定， N 最小6.4 FIR滤波器的等波纹逼近中国科学技术大学75通带截止频率： p=0.